基于3D 视觉的工件识别及无序抓取系统设计

陈顺强，廖 旭，罗 桢，李 波，黄传富，王 键，李 力，柏俊杰

（重庆科技学院 电气工程学院，重庆 401331）

随着工业信息化技术蓬勃发展，目前工业生产中多使用机械臂来代替人工完成工件的分拣、装配等任务。而在实际的工业生产中，工业机械臂的作业环境及需求相对复杂，例如机械臂的视觉部分经常会受到光照强度、相机成像距离、视点变化等因素的影响，而且一些特定的生产工艺下，还需要工业机械臂能从杂乱无章、相互遮挡或者重叠的物料中逐一完成抓取。对于上述条件限制，目前发展成熟的基于2D 相机搭配一般的工业机械臂抓取技术很难高效、准确地完成抓取任务，而且一般的工业抓取系统较为昂贵。

为了解决上述问题，目前已有很多学者提出可行的基于3D 视觉引导机械臂抓取的方法[1]。柯科勇[2]使用2 个结构光摄像头，将得到目标物件的深度点云数据进行三维重建，重建后的点云和模板点云进行配准，得到需要的抓取坐标，该方法缺点在于获取到点云数据存在一定的噪声和干扰，和模板点云比对必定存在差距，从而会影响到抓取坐标的准确性。WONG等[3]提出SegICP 方案使用CNN 网络对大规模点云数据进行处理，实现了对点云数据的分割和配准，但是该方法识别性和速度不能兼容。

为了提升基于3D 视觉[4]引导机械臂完成无序抓取的准确性和实时性，本文融合了一些效果较好的点云处理算法[5-7]，对深度相机采集到的点云数据进行滤波、分割、配准等处理[8-9]，得到携带信息量高的点云，再使用GPD 算法获取机械臂6DoF 抓取坐标[10]，将抓取坐标信息通过ROS 系统多机通信完成和机械臂的信息交互，引导机械臂完成无序抓取[11-12]。最后对该系统进行实验测试。

1 整体系统结构

针对基于3D 视觉的工件识别及抓取系统，本文提出了以下系统框架，如图1 所示。

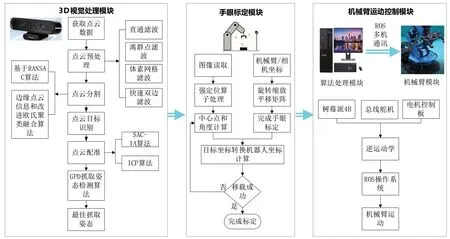
图1 系统整体框架图

基于3D 视觉引导机械臂无序抓取系统包括3D 视觉处理模块、机械臂运动控制模块、手眼标定模块3 个部分，其中3D 视觉处理模块为系统的核心部分，手眼标定模块为辅助部分，机械臂运动控制模块为执行部分。

2 3D 视觉处理模块设计

2.1 点云滤波处理

本文通过在上位机ROS 系统中订阅滤波话题，将深度相机获取的点云数据转化为PCD 处理格式，通过调用PCL 库中的半径滤波、离群点滤波、体素网格滤波对点云数据进行滤波处理。

通过直通滤波来过滤掉深度相机大视角下的干扰点云数据，减小深度相机正前方观测范围，滤波效果如图2 所示。

图2 直通滤波效果图

直通滤波已经将大范围发散的点云滤除掉，深度相机采集的数据会存在不同密度的点云集，采用离群点滤波去除主体点云数据周围存在稀疏的异常值，滤波效果如图3 所示。

图3 直通滤波效果图

直通滤波和离群点滤波对数据进行滤波后，已经取得了较好的去噪效果，但剩下的点云数据密度相对较大，大量的点云数据运算将会消耗时间和空间资源，因此本文采用体素网格滤波来对数据进行下采样，保留点云关键特征的基础上去除冗余信息，达到精简点云数据的目的。体素网格滤波效果如图4 所示。

图4 体素滤波效果图

2.2 点云分割

2.2.1 基于RNASAC 算法的平面分割

由于目标工件之间往往是相互堆叠的，为了使机械臂完成单一性的无序抓取，必须将目标点云数据进行分割处理，本文采取RANSAC 算法对点云数据进行平面分割，去除试验台平面及背景的干扰，分割效果如图5 所示。

图5 RANSAC 算法进行平面分割效果图

2.2.2 基于边缘点云信息和改进欧氏聚类融合算法的目标分割

使用传统的欧氏聚类算法对无序堆叠、相互粘连的工件点云数据进行分割时，若搜索半径r 值选取不当会出现过分割和欠分割的情况，而且分割时间较长。为提升欧氏聚类算法点云分割的鲁棒性、加快分割效率，本文提出一种基于边缘点云信息和改进欧氏聚类融合算法来进行目标分割。

（1）基于法向量夹角突变的边缘点去除

当2 个目标工件出现堆叠时，映射到其三维点云数据上，在空间中工件堆叠处边缘点云法向量会出现方向上的突变。基于该特性，本文对点云数据边缘点部分进行提取并去除，算法步骤如下：

① 使用KD-Tree 搜索构建工件点云p 的拓扑关系。

② 为目标工件构建点云模板库，设定法向量变化阈值u，领域半径r。

③ pi为目标工件点云中的任意点，pi计算该点的搜索邻域半径内相邻点法线夹角最大变化的均值δpi，若满足δpi>u 则定义该点为边缘点，反之为非边缘点。其中，n0表示法向量的方向；Φ 为点云法线夹角变化最大值，可表示为：

则邻域点法线夹角最大变化均值为：

④?对工件边缘点进行剔除，剔除效果如图6所示。

图6 边缘点剔除效果图

（2）对剔除过边缘点的点云数据使用改进的欧氏聚类算法进行分割

使用传统的欧氏聚类对点云进行分割，其分割效率最主要影响因素就是聚类阈值的选取。本文提出一种自调节阈值的欧氏聚类分割方法，提升分割效率。算法步骤如下：

① 选取目标点云中任一点pb作为聚类中心点，使用k-dimensional 算法快速pb搜索最近邻的N 个点；

② 判断选取的聚类中心点pb是内部点还是边缘点，若为内部点就可以增加距离阈值，反之减小距离阈值。本文使用聚类中心点pb到N 个近邻点的平均距离dm来判断pb为内部点还是边缘点，dm表达式：

自调节阈值dre和近邻点的平均距离dm存在密切关系，定义其关系表达式：

③ 通过上述公式得出自调节阈值dre，使用自调节dre替换初始聚类阈值，重复上述步骤对剩下的点云数据进行分割。

（3）填补边缘点云数据

使用自调节阈值欧氏聚类算法完成对剔除边缘的点云数据分割后，为了保障点云数据完整性，需要将剔除的边缘点云数据补回，目标数据点云分割结果如图7 所示。

图7 目标粘连时分割效果图

对于目标工件不同的摆放位置，做了50次分割实验，点云的分割准确率统计结果如表1 所示。

表1 50 次目标工件不同摆放位置分割准确率 %

采用传统的欧氏聚类算法和改进后的算法分别对随意摆放的工件点云数据做了300 次分割实验，并且进行分割精度和分割时间上的统计，实验结果如图8 所示。

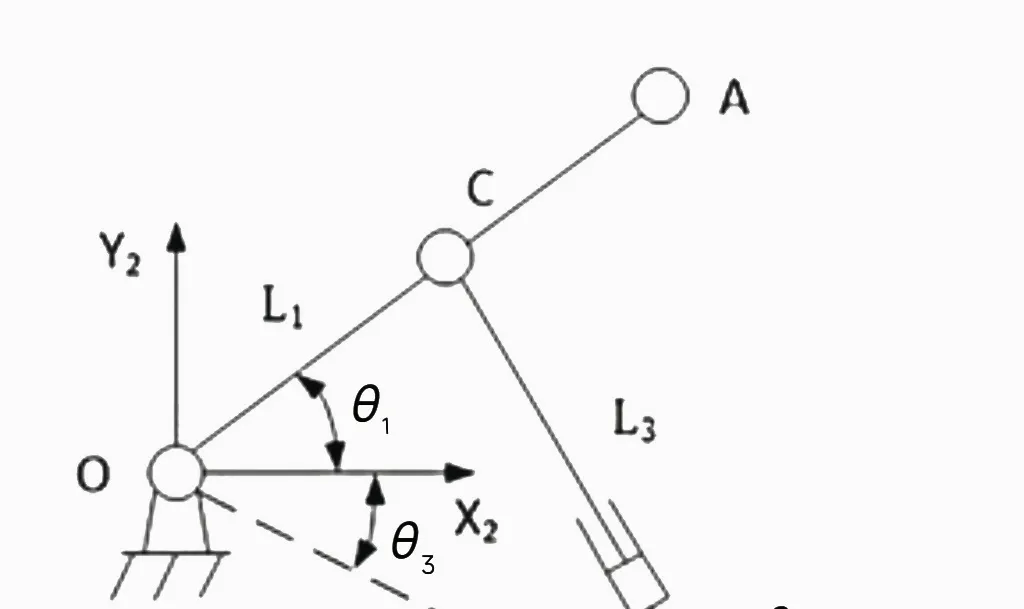
图8 分割算法改进前后分割准确率及时间对比图

由实验结果可知，基于边缘点云信息和改进欧氏聚类融合算法相对于传统的欧氏聚类算法分割时间平均降低50.6 ms，分割准确率平均提升3.2%。

2.3 点云目标识别及配准

2.3.1 改进FPFH 算法

本文对FPFH 算法进行改进，在FPFH 算法原本3 组特征法线夹角的基础上再引进1 组特征元素，该特征元素为查询点法向量与提取固定拟合平面的夹角。传统FPFH 算法和改进的FPFH算法局部坐标表示图如图9、10 所示。

图9 传统FPFH 算法局部坐标表示

基于改进的FPFH算法特征提取计算流程如下：

① 图10 中ps为需要计算FPFH 的点，pt为它的邻域内一点，ns和nt分别为其法向量，式中u 为ps点的法向量，该局部坐标3 个轴的计算方法如下：

图10 改进FPFH 算法局部坐标表示

② 由上诉公式得到点ps的一个局部坐标，n1

将原本FPFH 中的三元组扩充为四元组，分别为（α，Φ，θ，β）。

③ 分别计算ps与近邻点的四元组，通过统计得到ps的简化点特征直方图，记作SPFPs。以近邻点依次作为查询点计算出对应的特征直方图。

④查询点ps计算快速点特征直方图的公式如（13）所示，式中wi为权重（pq和pi之间的距离）。

⑤ 按照步骤1、2、3、4 计算点云中各点的4元组信息，分别将4 个元素对应的直方图连接起来，即为点云样本的改进FPFH 全局快速点特征直方图。

2.3.2 点云识别及配准实验

点云目标识别之前需要建立本地模板库，对同一物体的多个角度采集点云信息，然后计算其改进FPFH 计算特征直方图结果，并以PCD 文件格式保存下来，如图11 所示。

图11 不同视角下的目标与其改进FPFH 特征直方图

定义待识别目标与不同模板的改进FPFH 特征直方图的差异距离为d （Hh，Hk）均值，计算公式：

式中，Hh表示待识别目标的改进FPFH 特征向量；Hk表示点云模型库内点云模型的改进FPFH 特征向量为实验次数。差异距离d （Hh，Hk）均值越小即识别效果精确度越高。

使用本文提出的改进FPFH 以及模板库制作方式和传统FPFH 识别准确度（用d （Hh，Hk）值衡量）和识别速度对比。通过50 次实验计算统计数据均值如表2 所示。为拟合平面法向量，根据该坐标可以计算ps点的4 组特征表示：

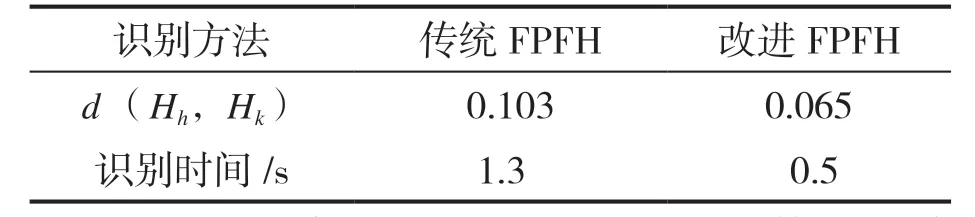
表2 传统FPFH 和改进FPFH 识别准确度、速度对比

本文分别使用改进前后的FPFH 算法联合ICP 算法对点云数据进识别配准实验，配准效果图如图12 所示。

2.3.3 GPD 最佳抓取姿态检测

对点云数据进行配准后，需要计算出最佳抓取坐标，本文使用GPD 算法拟合出最佳抓取坐标，在ROS 系统调用编译好的GPD 算法的话题。抓取位姿在ROS 插件RVIZ 中的可视化效果图如图13 所示。

图13 GPD 算法运行结果

3 抓取实验

在实际场景中，搭建了无序分拣系统，整个分拣系统主要由Astra Pro 深度相机、机械臂、机械臂控制器、上位机等组成。本文采用以树莓派4B 为主控，ROS 为操作系统，通过ROS 多机通讯将机械臂与上位机进行连接，通过订阅上位机传输抓取坐标的话题，来控制机械臂完成抓取，抓取系统工作流程过程如图14 所示。

将4 个待抓取工件摆放到桌面，分别针对工件无堆叠和有堆叠2 种场景进行50 次抓取实验，同时记录利用目标识别和位姿估计算法得到的位置坐标，并且统计识别坐标和实际坐标间的平均绝对值及相对误差，以及抓取时间和抓取准确度。抓取实验数据如表3 所示。

表3 抓取实验数据表

其中实际坐标与识别坐标平均相对误差由公式（15）求得：

式中，n 为总实验次数；x，y，z 为实际坐标；x'，y'，z'为识别坐标。

实际坐标与识别坐标平均相对误差越小，抓取精度越高。由表3 数据得出50 次抓取实验的平均相对误差为0.9%~1.4%，抓取时间在5 s~8 s间，其中工件无序无堆叠场景下的抓取成功率在94.2%以上，而工件有序有堆叠场景下的抓取平均成功率为88.2%。

为了验证本文提出的基于边缘点云信息和改进欧氏聚类融合对目标分割算法以及改进的FPFH 全局特征提取，对该3D 无序抓取系统的效率提升度。本文使用传统的欧氏聚类算法以及FPFH 算法来完成点云数据的处理，并同样使用该套系统完成抓取，进行50 次工件有堆叠情况下动物抓取实验。改进前后抓取时间及实际坐标与识别坐标相对误差如图15 所示。

图15 改进前后抓取时间及抓取姿态相对误差数据对比

4 结论

本文提出一套基于3D 视觉的机械臂无序抓取系统方法，并通过实验验证改进算法的有效性。基于边缘点云信息和改进欧氏聚类融合算法相对于传统的欧氏聚类算法点云数据分割准确度提升3.4%，分割时间平均提升50.8 ms。扩充FPFH 的特征元祖，并且建立点云识别的模板点云库，使特征点云识别准确度提高。将改进、优化的算法和传统算法应用到同一个抓取系统里进行效果比对，验证了本文改进的算法能够达到优化点云数据处理效果。实验结果表明，本文所设计的基于3D 视觉的无序抓取系统能从工件堆叠的场景中成功抓取目标，而且抓取系统的准确度提升5.2%，抓取系统运行时间降低3 s~6 s。