基于工件振动和刀具结构的周铣表面形貌分析与预测
刘扬, 秦国华, 吴竹溪, 娄维达, 赖晓春
(1.南昌航空大学 航空制造工程学院, 江西 南昌 330063; 2.江西省教育厅 江西省教育国际合作与教师发展中心, 江西 南昌 330083)
0 引言
动态的切削过程势必造成工件产生振动,影响工件的加工表面形貌,进而影响零件的物理、机械性能以及实用寿命。
赵军等[1]基于自由曲面方程运算出刀具刃线运动包络面,对球头铣刀加工的表面形貌进行了建模和仿真,结果表明:在工件加工面为平面时刀轴摆角的选择对表面形貌有较大影响;加工面为自由曲面时,刀轴摆角的选择对表面形貌影响不大。Liu等[2]开发了一种铣削加工表面的仿真系统,使刀具-工件相互作用随刀具运动的动态跟踪成为可能,通过对刀具中心运动和刃口形状的修改,将刀具跳动和磨损的影响分别纳入开发的模型中,从而更准确地描述被加工表面的微观特征。Lavernhe等[3]利用N-buffer方法建立了表面形貌的预测模型,经预测模型分析表明,刀具倾角对三维形貌的影响较大。Fernando等[4]在量纲分析与有限元分析的基础上,对AISI H13钢球头铣削表面形貌进行数值模拟,并用铣削实验验证了该模型的有效性。Schmitz等[5]研究了端铣加工过程由刀具的位置偏移以及刀具倾斜所导致的刀具安装误差对加工工件表面形貌的影响,通过仿真验证了跳动量、表面粗糙度、稳定性和表面定位误差之间的关系。Chen等[6]建立了基于微细铣刀几何特征的曲面生成模型,研究了轴向跳动和径向跳动对表面形貌的影响。Zhang等[7]采用接收耦合法得到动态特性函数,并结合铣削力模型计算刀具的动态挠度,提出了一种新的表面形貌模型,通过将刀具偏转引入微侧铣刃轨迹方程,分析认为影响微侧向铣削表面形貌的最重要因素是主轴转速、进给速度、径向切削深度和铣削方法。Arizmendi等[8]提出了一种预测面铣表面三维形貌的新方法,结果表明端面铣刀刀片之间的轴向跳动显著影响表面形貌。Wang等[9]考虑了刀具平行轴偏移和位置角的影响,改变了椭圆中心和切削刃交点的位置,通过建立表面形貌预测模型分析了影响粗糙度发展趋势的因素。上述研究工作主要是在刀具切削刃几何形状的基础上,进一步考虑了刀具的跳动、偏转等对加工表面形貌的影响。
Zeroudi等[10]建立了自由铣削时刀具的切削力预测模型,通过考虑切削力对加工工件表面形貌的影响,建立了铣削工件表面形貌的重组模型。Chen等[11]提出了一种预测薄壁零件弹性变形后表面形貌的数值模型,针对切削过程中的几何特征建立了薄壁零件的切削力模型,研究了刀具-工件之间的啮合关系。Peng等[12]建立了一种考虑刀具倾斜、颤振、跳动、切削力和材料的塑性变形模型,并证明了模型推荐的参数可以很好地控制三维表面形貌。宋文刚等[13]采用表面算术平均高度和表面最大高度对表面形貌进行了表征,建立了考虑工件初始表面几何状态的切削层模型,利用两工步铣削试验对切削层模型进行了验证,结果表明工件初始表面几何状态与第二工步铣削的铣削力和表面粗糙度参数呈正相关关系。白利娟等[14]以刀尖为研究对象,利用振动辅助铣削获得的仿真刀尖轨迹生成生物表面形貌,与实验结果对比表明振动辅助铣削表面形貌在仿生表面的加工领域具有可行性。Lu等[15]基于微铣刀的实际切削轨迹和柔性变形建立了表面形貌仿真模型来预测表面粗糙度,并通过实验验证了模型的准确性。梁鑫光等[16]利用球头铣刀刀刃的三维次摆线轨迹,通过等间隔的距离、时长分别读取工件表面的残留高度、刀具振动响应,实现了加工表面名义形貌建模与系统动态响应轨迹仿真。张国华等[17]采用金属切削理论对椭圆振动切削过程和三维切削模型进行了分析,结果表明切削过程中相邻两转之间不同的相位差特征值对最终表面形貌有着重要影响。Costes等[18]使用非接触式位移传感器测量出铣削过程中刀具的高频振动信号,通过提取走刀步长和刀具中心点,建立了刀具变形的力学模型,从而获取到工件的表面形貌特征。
以上研究工作尽管考虑了刀具的变形、振动等因素对铣削形貌造成的变化,却没有从夹具装夹布局的角度研究工件加工表面形貌的形成规律。
本文首先根据工件与夹具的单向接触这一实际条件建立装夹布局的运动学模型,利用能量法推导出工件在铣削过程中的振动微分方程。然后提出振动微分方程的解耦方法,计算出工件位置的偏离。最后,建立周铣过程中切削刃的运动轨迹方程,结合工件位置偏离提出工件表面形貌的仿真方法。
1 装夹布局的振动微分方程
在加工过程中,刚性工件将受到重力Fg、加工力Fc、扭矩Mc等外载作用。为抵抗这些外载的破坏作用,必须给工件施加夹紧力。
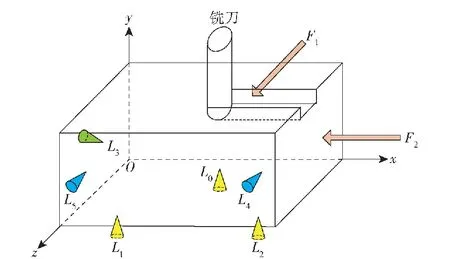
假设工件由m个定位元件定位后,施加n个夹紧力Fj(1≤j≤n)。将工件-定位元件等效为半弹性接触模型,则第i个定位元件可以视为在法向ni=[nxi,nyi,nzi]T和两个切向ti=[txi,tyi,tzi]T、ai=[axi,ayi,azi]T上忽略质量的阻尼弹簧,刚度和阻尼系数分别为kni、kti、kai和cni、cti、cai。记rw=[xw,yw,zw]T、Θw=[αw,βw,γw]T分别为工件坐标系Owxwywzw相对于全局坐标系Oxyz的位置和方向,如图1所示。假定rw=[xw,yw,zw]T为工件上任意点P在Owxwywzw坐标系中的坐标,则P点在Oxyz坐标系中任意时刻的姿态为r=rw+T(Θw)rw,其中
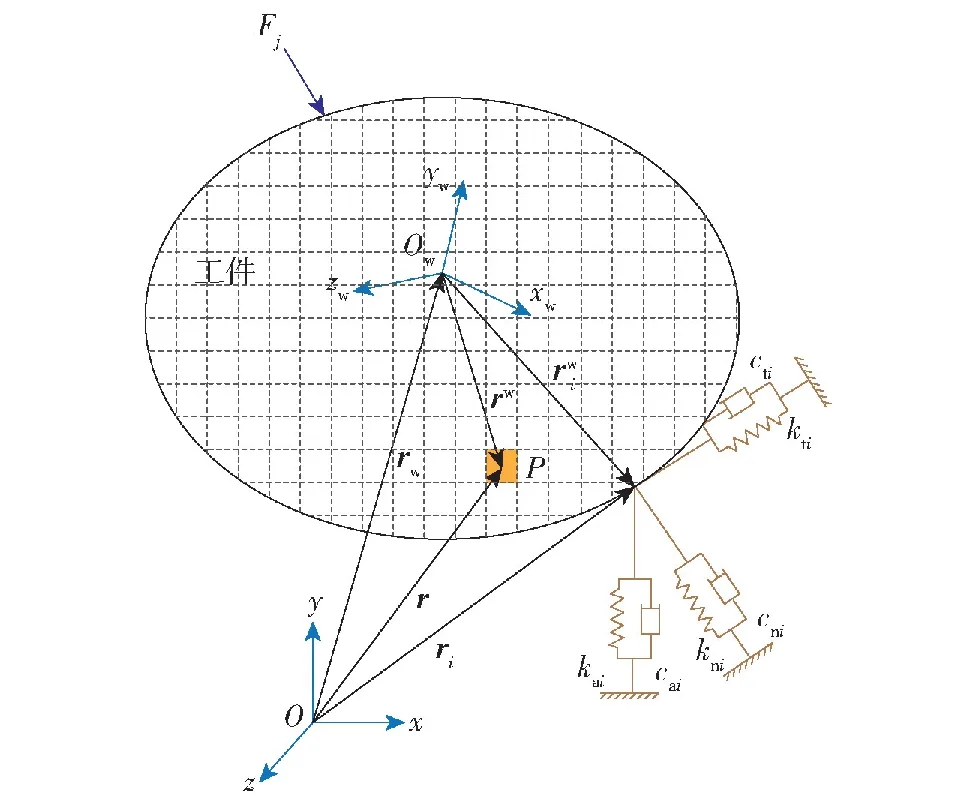
图1 工件振动模型

由此可以得到工件在装夹布局系统中的振动微分方程[19],即
(1)
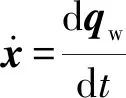
值得注意的是,工件装夹的目的旨在给工件施加夹紧力,保证定位时获得的工件相对于刀具的位置不变。为此,应使得式(1)中第i个定位元件的支撑反力满足
(2)
为更简单地描述式(2),采用矩阵形式进一步表达为
kNψdqw≥0
(3)

2 振动方程的解耦与求解
在个别情况下,M、C、K都是对角矩阵,这时式(1)的求解较为容易,但不具备普遍性。实际的加工过程中,振动系统的微分方程都会出现耦合项。因此,振动方程的解耦方法是解算工件位置偏移的关键。
2.1 振型向量的正交性
由式(1)可知,不考虑阻尼自由振动响应的表达式可以表示为
(4)
在系统的自由振动中,假设所有的质量均作简谐运动,则方程的解可表示为
xs=A(s)sin(ωst+φs)
(5)
式中:xs表示第s阶振型的诸位移的列阵;A(s)表示第s阶振型中各点的位移最大值或振幅向量;ωs表示第s阶振型的固有频率;φs为第s阶振型的相角。
将式(5)代入式(4)中,可得
(6)
由此得出对应固有频率ωs和ωs的主振型A(s)和A(f)下述两个方程式:
(7)
(8)
用(A(f))T左乘式(7),再转置式(8)后右乘A(s),可以得到
(9)
(10)
这样,由式(9)减去式(10),可得
(11)
(12)
当s≠f且特征值ωs≠ωf时,要满足式(11)、式(12),必然有以下关系:
(A(f))TMA(s)=(A(s))TMA(f)=0
(13)
(A(f))TKA(s)=(A(s))TKA(f)=0
(14)
式(13)、式(14)表明,不相等的固有频率两个主振型之间存在关于质量矩阵M和和刚度矩阵K的正交性。
当s=f时,式(11)、式(12)对任何值都是成立的,使
(A(s))TMA(s)=Mps
(15)
(A(s))TKA(s)=Kps
(16)
式中:Mps和Kps分别为第s阶的主质量和主刚度,均为常数,它们取决于特征向量A(s)是如何归一化的。
将A(s)归一化后依序排成各列,得到模态矩阵Ap,可表示为如下形式:

(17)
式中:λ为最大振型阶数。
将式(17)代入式(15)、式(16),可得
(18)
(19)
式中:Mp和Kp分别为主质量矩阵和主刚度矩阵,两者均为对角矩阵。
2.2 方程解耦
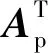
(20)
引用正交关系,将式(18)、式(19)代入式(20),可得
(21)
式中:
(22)
(23)
由于主质量矩阵Mp和主刚度矩阵Kp均为对角矩阵,利用主坐标描述系统的运动微分方程则不存在耦合。
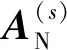
(24)
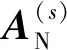
(25)
式中:μs为一个待定常数,称为正则化因子。
将式(25)代入式(24)中,可得
(26)
求出μs后代入式(25),得正则振型矩阵AN为

(27)
用AN按照式(18)计算得到的正则质量矩阵MN是一个单位矩阵I,即
(28)
又由式(7)、式(8)可知
(29)
(30)

(31)
对于具有阻尼为C的运动方程,正则阻尼矩阵CN可表示为
(32)
在实际工程应用中,大多数情况下CN都不为对角线矩阵,但工程上大多数振动系统中阻尼都较小,而且由于各种阻尼比较复杂,为使正则振型矩阵对角化,最简单的办法就是将其非对角线元素的值改为0,即
(33)
式中:CNss为第s阶正则振型的阻尼系数。
在实际进行振动分析时,阻尼系数CNss通常用实验或实测给出各阶振型的阻尼比ξs。因此结合式(32),可得
(34)
2.3 方程求解
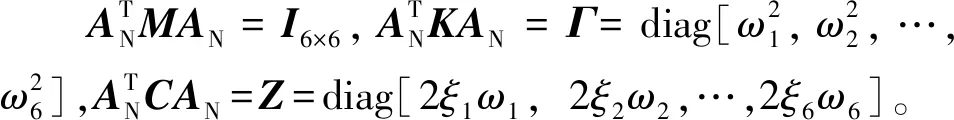
(35)
式(35)的解耦形式为
(36)
式中:1≤s≤6。
利用Duhamel积分可分别求解每一个主坐标,即
(37)
式中:t为系统时间;η为系统时间内任意时刻。
因此,振动微分方程的解为
dqw=ANXp
s.t.
kNψdqw≥0
(38)
3 刀刃运动轨迹
除工件的动态装夹布局,影响工件加工表面形貌的另一大因素是刀具切削刃的几何形状。建模的关键点在于求解出刀刃在空间中的运动轨迹。
周铣过程如图2所示,Oxyz、Owxwywzw分别为全局坐标系、工件坐标系,而Ocxcyczc、Osxsyszs分别为刀具坐标系、主轴坐标系。一般地,为方便起见,在建立坐标系时,应使Oxyz与Owxwywzw重合;R为铣刀半径,γ为螺旋角,e为刀具偏心距,α为旋转角度,vf为刀具进给速度,φj为第j个刀齿的初始角度,w为刀具转速,刀具顺铣时w取正值,逆铣时w取负值,P为切削点,ABCD为切削区域。

图2 周铣切削刃运动示意图
若刀具有z个刀齿,则第j个刀齿的初始角度可表示为
(39)
这样,铣刀第j个刀刃上任意点P在Ocxcyczc坐标系的坐标应为
(40)
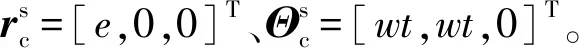
(41)
此外,在任意时刻t时,主轴沿进给方向y移动了vft。若在初始时刻Osxsyszs与Oxyz重合,则在t时刻,Osxsyszs相对于Oxyz坐标系的位置、方向分别为rs=[0,vft, 0]T,Θs= [0, 0, 0]T,则第j个刀刃上P点在Oxyz坐标系中的坐标为
(42)
4 工件表面形貌
对工件上任意一点的位置r进行求导可知,在t时刻,若工件由装夹布局振动引起dqw的位置变化,则工件上任意一点的位置变化应为
dr=Edqw
(43)
式中:
(44)
则在t时刻,若刀齿上P点在切削区域ABCD范围内沿背吃刀量方向上,则当且仅当P点坐标在理论切削平面与待切削平面之间,表明P点参与了切削,如图3所示。图3中ap为轴向切削深度。

图3 坐标平面Oxy内的表面成形示意图
根据式(42)、式(43)可知,切削平面上P点的坐标rP=[xP,yP,zP]应为
(45)
式中:
(46)
显然,式(45)很难求解处理,故采用离散方法进行求解。表面形貌离散算法步骤如下:
步骤1离散待切削平面。
分别以步长Δy、Δz将工件均匀划分成m×n个网格,用矩阵存储每个网格节点的坐标值分别为x(u,e)、y(u,e)、z(u,e),其中u=1, 2, …,m+1,e=1, 2, …,n+1。
步骤2离散切削时间和切削刃。
根据工件网格精度设置时间离散步长Δt以及切削刃离散点数l,一般取Δt=min{Δy, Δz}/(wR),l=hT/min{Δy, Δz},hT为铣刀切削部分的有效长度,以保证切削刃离散微元在加工平面内的投影不超过工件的网格间距,并且在单位时间步长内最多扫过一个工件网格点。
步骤3初始化切削时间t=0 s。
步骤4计算当前时间的装夹布局振动。
根据式(43)获得切削平面上每个网格节点的坐标r(u,e)=[x(u,e),y(u,e),z(u,e)]T。
步骤5初始化切削刃号j=1。
步骤6初始化离散点号k=1。
步骤7判断离散点是否在加工区域内?
根据式(42),计算切削刃上离散点Pk在当前时间的坐标值(xk,yk,zk),并判断其是否在待加工平面内。若是则转步骤8,否则转步骤10。
步骤8搜索离切削刃离散点最近的待加工平面网格节点。当离散点的位置(yk,zk)与网格点的位置(y(u,e),z(u,e))重合或者最接近时,该离散点与网格点相对应。
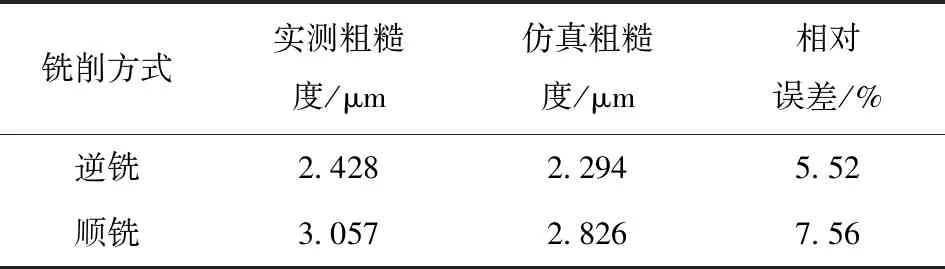
步骤9判断切削刃离散点的切削情况。比较最近网格节点x(u,e)与切削刃离散点Pk的xk之间的关系,如果xk 步骤10判断是否为最后一个离散点?若是则转步骤11;否则计算下一离散点k=k+1,转步骤7。 步骤11判断是否为最后一个切削刃?若是则转步骤12;否则计算下一个切削刃j=j+1,转步骤6。 步骤12判断是否为最后一个时刻?若是则结束计算过程,存储的x(u,e)、y(u,e)、z(u,e)即形成切削表面形貌;否则计算下一个时刻,转步骤4。 采用两个典型实例详细说明表面形貌的计算,并验证表面形貌计算结果的正确性。第1个实例将工件固紧在工作台上,忽略装夹振动带来的影响,直接测量表面粗糙度值进行验证;第2个实例来自于参考文献[20],通过验证接触力大小间接验证计算过程的有效性,并给出考虑装夹振动的表面形貌。 图4为一立铣刀周铣工件的铣削实验现场图与实验结果图。工件的材料为铝合金,杨氏模量Ew=207 GPa;刀具的材料为硬质合金,杨氏模量ET=530 GPa,其他参数如表1所示。由装夹方案及刀具参数可知,刀具以及工件在周铣加工过程中的刚性都较强,因此忽略二者在加工过程中的振动。 表1 周铣加工参数 图4 周铣实验 不考虑工件装夹布局在加工过程中对工件铣削表面形貌产生的影响,即dqw=0,单独验证周铣算法的有效性。 根据表1设置铣削加工参数。设Δy=Δz=0.05 mm,将铣削表面均匀划分为120×120个网格。用矩阵x(u,e)、y(u,e)、z(u,e)存储每个网格节点的坐标值。之后计算离散时间间隔Δt=min{Δy, Δz}/(wR)=9.55×10-5s,切削刃离散点数l=hT/min{Δy, Δz}=120。 由于不考虑工件振动,可以对表面形貌离散算法进行简化,不考虑算法中的步骤4,经计算后得到表面形貌结果如图5所示。 图5 不考虑振动的表面形貌 图6给出了在稳态加工情况下逆铣和顺铣的实际加工表面。通过对比实际加工表面和仿真形貌结果可以看出,表面形貌离散算法的计算结果与实际加工情况非常吻合。 图6 稳态加工中的实际加工表面(左为实际加工表面,中为黑白仿真表面,右为彩色仿真表面) 为进一步从数值上进行对比,在由中国上海精密仪器仪表有限公司生产的粗糙度轮廓仪JB-6CA上测量铣削表面的粗糙度,如图7所示,测量结果如图4(b)所示。将实测及计算结果的轮廓算术平均偏差Ra列入表2中。通过对比可知,逆铣表面形貌离散算法获得的结果具有较好的准确度。 表2 周铣形貌仿真实验验证结果 图7 粗糙度测量 采用半径R=9 mm的铣刀,以轴向切深ap=3 mm、每齿进给量f=0.05 mm、铣削速度v=100 mm/min 在工件表面上铣槽[19-20],如图8所示。图8中,F1、F2为夹紧力,L0~L5为定位元件。工件的外形轮廓尺寸为220 mm×122 mm×112 mm,材料为7075-T6铝合金,工件的杨氏模量和泊松比分别为Ew=70 GPa与bw=0.334;工件重力为Fgrav=[0 N, 59.73 N, 0 N]T,质心位置为rgrav=[110 mm, 56 mm, 61 mm]T,加工力和加工扭矩[20]分别为Fmach=[-131 N, -55 N, 232 N]T,Mmach=[0 N·m, 2.77 N·m, 0 N·m]T。 图8 3-2-1装夹方案 为保证加工过程的顺利实现,分别在r1=[110 mm, 60 mm, 0 mm]T和r2=[220 mm, 60 mm, 60 mm]T处施加夹紧力F1= 640 N和F2=670 N。各定位元件的位置与单位法向量如表3所示。平头定位元件由硬质钢制造,定位元件杨氏模量和泊松比分别为Ef=207 GPa与bf=0.292,定位元件半径Rf=6 mm,长Hf=12 mm,阻尼系数cf=7 000 N·s/m。 表3 定位元件的位置与法向量 根据工件质量、定位元件弹性模量等数据,容易得到刚度矩阵、质量矩阵、阻尼矩阵分别为 (47) (48) (49) 结合质量、刚度与阻尼矩阵及式(1)并解耦,可以得到6个2阶微分方程,其中动态外载F(t)=[801 N, 114.73 N, -872 N, -9.1024 N·m, 22.08-0.3867tN·m, -0.091 7t-0.324 2 N·m]T,切削时间为0 s≤t≤132 s,根据式(37)可求得工件的位置偏移随时间t的变化,结果如图9、图10所示。 图9 不考虑阻尼的工件位置变化 图10 考虑阻尼的工件位置变化 通过比较可以发现,考虑阻尼与不考虑阻尼两种情况工件的位置偏移趋势大致是相同。但不考虑阻尼时,工件位置偏离的变化是不稳定的;考虑阻尼时,工件位置偏离是稳定的。 由于工件位置的振动偏移是由各定位元件的位置偏移造成的,工件振动的计算值可通过测量定位元件处支承反力来间接保证。实验装置图如图11[20]所示。各定位元件处支撑反力的实验测量值如图12(a)[20]所示,静力学模型计算值如图12(b)[21]所示,根据式(3)计算出来的动态支承反力如图12(c)所示,图中标号0~5分别表示定位元件L0~L5。由图12分析比较可知,定位元件处的支承反力静力学模型计算值的误差为15%[20],动力学模型计算值更接近于实验结果,误差约在12%以内,精度提高了3%。显然,无论是支撑反力的变化趋势还是力的大小,两者均非常吻合。 图11 实验装置 图12 支撑反力 根据本文提出的表面形貌离散算法,选取槽的任一侧面进行形貌仿真,经公式计算刚度G=πER2/H,式中H为定位元件长度,这时定位元件的刚度约为刀具的一半,因此主要考虑装夹布局振动对表面形貌造成的影响,其结果如图13、图14所示。 图13 逆铣形貌 图14 顺铣形貌 由图13、图15可以看出,不考虑装夹布局和考虑装夹布局的三维形貌大致相同。但不考虑装夹布局时整体切削深度更深,这是因为工件是刚性的,考虑装夹布局时工件振动会导致工件整体发生位置偏移。 图15 截面轮廓对比 从表面质量的角度来看,在考虑装夹布局对加工表面形貌的影响时,仿真表面明显更为不平整。通过计算,不考虑装夹布局时逆铣和顺铣的轮廓算术平均偏差Ra分别为5.956 μm和6.358 μm,考虑装夹布局时逆铣和顺铣的轮廓算术平均偏差Ra分别为6.237 μm和6.549 μm,计算精度分别提高了4.72%和3.00%。 1) 将工件与夹具之间的接触模式等价为线性弹簧-阻尼系统,建立了工件装夹布局模型。利用能量法建立了工件的振动微分方程,并根据加工过程中接触力必须为压力这一工况,利用胡克定律推导出了工件-夹具装夹布局的单项接触约束条件。 2) 根据机械振动学中的解耦方法,利用坐标转化法提出在约束条件下振动微分方程的模态分析求解方法,以实现工件位置偏离的预测。 3) 基于运动齐次坐标的变换矩阵和矢量运算法则,建立了周铣切削刃的运动轨迹方程,给出了周铣加工表面形貌的离散仿真算法。 4) 在不考虑装夹布局引起的工件振动的情况下,用实验验证了形貌仿真算法,逆铣和顺铣粗糙度的相对误差分别为5.52%和7.56%;在考虑装夹布局的情况下,用支承反力验证了定位元件位置偏移的有效性,模型的误差大约在12%以内,与静力学模型相比,精度提高了3%,并对两种情况下的形貌进行了仿真对比。 5) 在实际加工过程中,若刀具切削部分较长,此时相较于装夹方案,刀具振动对表面形貌的影响更为严重,这也是今后研究的重点方向。5 应用实例
5.1 不考虑振动的表面形貌





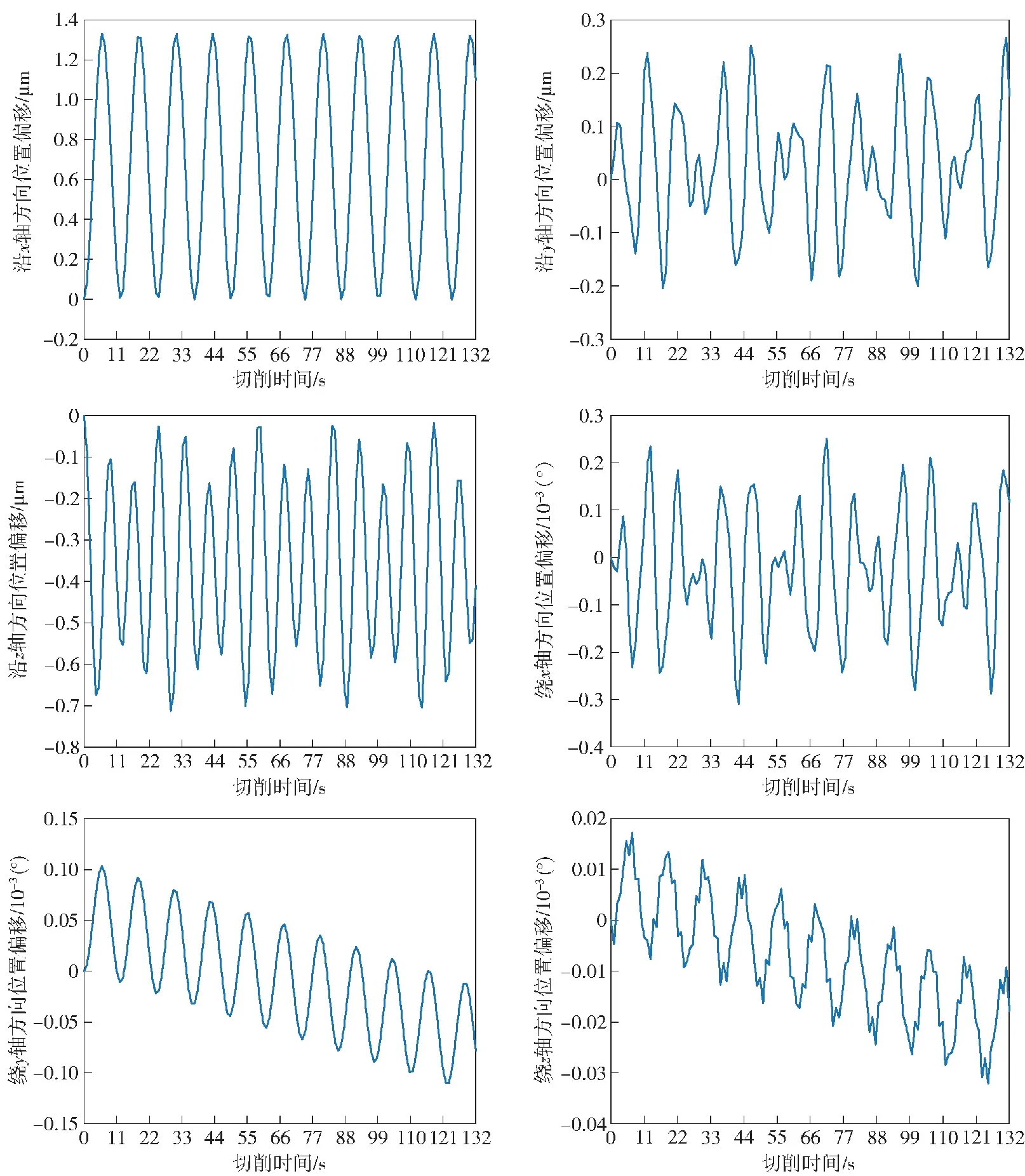
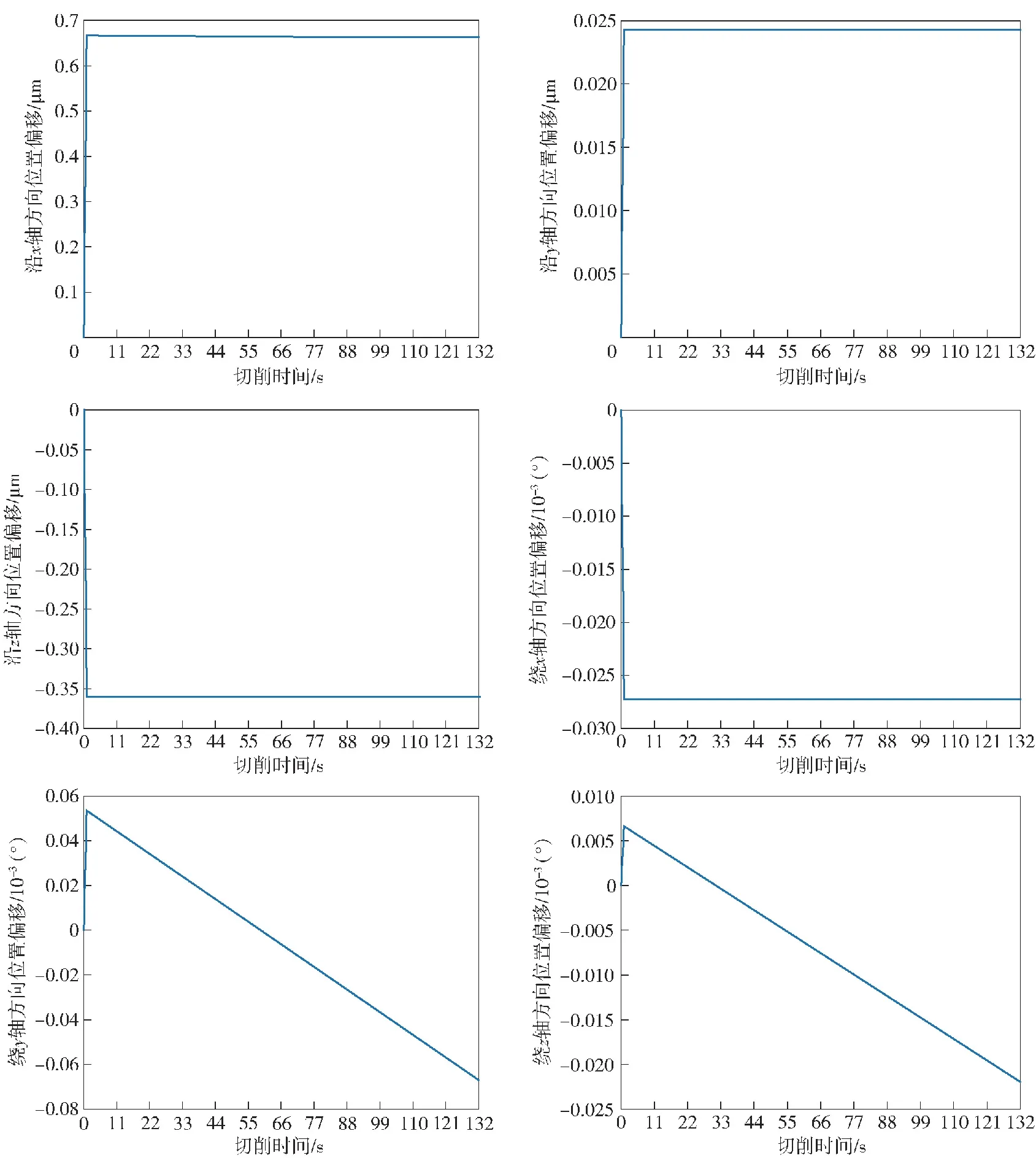
5.2 考虑振动的表面形貌






6 结论

