基于IMU-GNSS-VO的输电线无人机巡检定位和目标跟踪自适应方法

2023-08-05 08:08:28朱长荣吕文超单超王伟范江涛孙铭阳范延赫葛磊蛟

电力建设 2023年8期

朱长荣, 吕文超, 单超, 王伟, 范江涛, 孙铭阳, 范延赫,葛磊蛟

(1.国网冀北电力有限公司唐山供电公司,河北省唐山市 063099;2.天津大学电气自动化与信息工程学院,天津市 300072)

0 引言

随着架空输电线路的不断扩建和覆盖范围迅速增加,输电线路的区域环境愈加复杂,使得架空线输电线路的运维更加困难。传统的输电线路巡检方法强度高、周期长、危险性高、巡检面积大,难以满足现代电网发展需要。无人机(unmanned aerial vehicle,UAV)技术正在不断发展,凭借机动性强、控制简单、形式多样、效率高、成本低等优点,已经广泛应用于输电线路的巡检和侦察[1-2]。无人机采集数据的位置和高度取决于操作人员的视野和传感设备的检测结果。因此,无人机对架空输电线路的巡检很大程度上依赖于控制人员的飞行控制水平,对人工操作较高的依赖程度会导致定位精度偏低、航拍效果差和状态诊断精度低等问题[3]。这在很大程度上限制了无人机的工作性能,若无法很好地利用无人机机动性强、控制灵活、效率高等优势,常常出现无人机巡航偏离、返回原地偏差大等系列问题,迫切需要对无人机巡检精准定位技术进行深入研究。

目前可用于自主导航的传感器包括惯性传感器、视觉传感器、卫星导航传感器等。传感器是UAV自主导航系统的核心,是实现无人机自主智能的基本保证[4],也是输电线无人机巡检的基本信号输入来源。然而卫星信号易受到城市建筑物和复杂环境干扰;在大雾、大雪和灾难场景中,视觉传感器缺乏足够的特征点;惯性传感器面临着长期误差累积等问题[5]。因此在当今背景下,单一类型的传感器无法满足复杂场景中UAV的自主定位要求,多传感器融合方法利用不同传感器之间的互补优势[6]可以消除这一缺陷,从而获得最优估计,保证自主定位系统的可靠性和实时性。

多源融合定位算法包括顺序滤波、分散滤波、集中卡尔曼滤波等。联邦卡尔曼滤波作为一种分布式多源融合滤波方法,可以在多源融合模式下实现即插即用,从而保证系统定位的完整性和准确性。文献[7]基于惯性测量单元(inertial measurement unit, IMU)、全球导航卫星系统(global navigation satellite systems, GNSS)、视觉测程(visual odometry, VO)传感器,设计了一种多元融合因子图优化算法进行无人机定位状态估计。文献[8]提出了一种基于IMU、全球定位系统(global positioning system,GPS)、VO的无人机容错相对导航方法,用于无人机的协调编队飞行,有效提高了系统的相对导航精度和容错能力。文献[9]提出了一种基于卡尔曼滤波的无迹导航算法,用于解决实际的舰载无人机自主起降问题。结合GPS/惯导/视觉三部分测量信息,在考虑海面运动数学模型的条件下完成相对运动状态的估计过程。

但是,在输电线无人机巡检实际应用中,局部系统的性能和估计精度会随着复杂的导航环境不断变化,而传统的卡尔曼滤波信息共享系数是固定的,意味着随着环境复杂化,将无法满足任务要求。为了提高联邦滤波器的性能,文献[10]在对无人地面车辆导航的可观测性分析基础上,提出了一种新的滤波方法,该滤波器具有时变信息共享系数。文献[11]采用粒子群算法对基于区块链技术的导航系统进行了优化,但是算法兼容性不强。文献[12]在分析高动态环境下联邦滤波器的误差协方差矩阵和观测矩阵的基础上,设计了一种新的动态矢量形式信息共享方法。文献[13]提出了一种基于联合卡尔曼滤波器的多源信息融合定位算法,通过与集中式卡尔曼滤波器进行比较,验证了提出的算法具有容错性并减少了所需的计算量。文献[14]提出了一种自适应联合滤波算法,该算法可以使用先前的信息计算信息分布系数,并实时调整信息分布系数。文献[15]提出了一种自适应联邦滤波算法,该算法可以利用之前的经验计算信息分布系数,并实时更新。文献[16]设计了一种基于预测残差的信息因子自适应分配算法。然而,现有研究大多侧重于特定场景和单个传感器的故障,缺乏对不同场景和不同类型传感器故障的讨论。本文提出的鲁棒自适应算法适用于具有可变传感器组合的类似场景。

由于飞行高度变化、飞行范围广和背景复杂,无人机目标识别和跟踪容易不稳定。因此,如何设计一种更为稳定、精确的识别和跟踪算法是无人机目标跟踪中的一个具有挑战性的问题。在过去的十年中,已经提出了各种电力线跟踪方法,包括基于补丁检测的[17]、基于GPS路线点的[18]和基于电力线检测的[19-22]。基于电杆检测的导航在不提供沿电力线导航的特定方法的情况下检测电杆。因此,它们不适用于电力线检查。此外,因为输电线非常细而且缺乏丰富的特征,因此现有的对象检测/跟踪方法不能直接应用于输电线巡检。专为电力线检测设计的方法[19-22]在现实世界中表现不佳。通常,电力线检测步骤包括边缘检测和霍夫变换。在传统的电力线跟踪解决方案中,对其边缘检测算法手动设置阈值[19-21]。然而,固定的阈值可能会导致这些算法在复杂和变化的背景下失效。

综上所述,本文提出了一种无人机输电线巡检定位与目标跟踪方法。首先,结合鲁棒等效权值和子滤波器自适应共享系数,提出一种基于联邦卡尔曼滤波的鲁棒自适应定位算法来实现无人机自主定位;然后,引入了一种参数映射方法来将最佳检测数与相应的背景关联,有效调整检测算法的阈值,提高输电线检测和跟踪的精度。最后,结合唐山地区实际案例,对精度进行分析和比较,验证本文方法的有效性。

1 输电线无人机巡检精准定位技术

1.1 多源融合模型

1.1.1 误差状态卡尔曼滤波器

与经典卡尔曼滤波器相比,误差状态卡尔曼滤波器(error state Kalman filter, ESKF)可以将误差状态约束在接近原点的位置,从而避免可能的参数奇异性和万向节锁定问题,并确保参数线性化。本文基于ESKF对视觉/惯性导航和卫星/惯性导航的松散组合进行了建模。与经典的卡尔曼方法类似,ESKF执行预测和测量更新。基于IMU模型对预测模型进行运动学更新,并且基于VO和GNSS测量数据对测量结果进行更新。

UAV测量更新公式如下:

zk=Hkxk+vk

(1)

式中:zk为状态修正值;Hk为测量矩阵;xk为状态值;vk为速度。

GNSS测量数据被转换至导航坐标系,测量矩阵为:

(2)

(3)

(4)

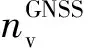
VO测量数据通过位姿计算从原始图像获得位置和姿态值,测量矩阵如式(5)所示:

(5)

(6)

(7)

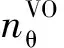
1.1.2 融合模型

联邦滤波的基本思想是选取一个信息全面、输出速率高、可靠性有保证的输入源作为参考源,和其他输入源两两组合进行局部滤波,再将局部滤波与主滤波器按信息原理进行融合。UAV数据测量常用GNSS和VO传感器,因此将GNSS与VO分别与IMU组合。

考虑到保证导航系统容错性和可靠性的需要,本文采用分布式滤波方法。图1给出联邦卡尔曼的经典融合反馈模式[23]。分别使用GNSS/IMU和VO/IMU建立两个子滤波器,最后融合两个子滤波器的数据来估计无人机导航状态。

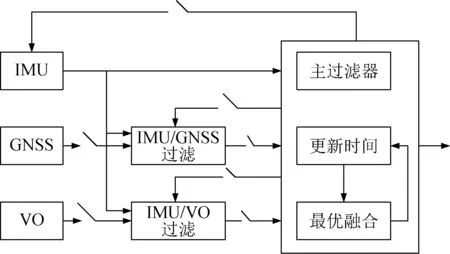
图1 联邦卡尔曼滤波器Fig.1 Federated Kalman filter

1.2 鲁棒自适应滤波

在复杂环境中,考虑到随机动态系统的测量值存在误差,甚至是粗误差,噪声的统计特性将发生变化,这将降低卡尔曼滤波的精度[24],甚至会导致发散。在这种情况下,子过滤器数据的可用性降低,甚至完全消除。应考虑在主滤波器的数据融合之前对子滤波器进行残差测试和鲁棒性处理,以减少观测的不可用性。不可用的观测值与主过滤器隔离,以免污染整个过滤过程,从而提高整个系统的准确性和容错性。

1.2.1 鲁棒等效权值滤波

系统状态残差由模型误差和观测误差决定。当模型误差较小时,用残差表示观测误差,用鲁棒等效权系数来改变观测可用性增益[25-27]:

(8)

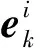
归一化处理过程如下:

vi=(ei)T(wi)-1ei

(10)

式中:vi、ei、wi分别为第i个子滤波器残差归一化结果、残差、协方差方程。

式(11)中引入IGG3权函数μi进行鲁棒处理,利用系统归一化残差自适应调整剩余增益矩阵。

(11)

式中:vi服从标准状态分布:vi～N(0,1),对超过95%置信水平的观测值进行稳健处理,其中k0设为1,k1设为2。在对鲁棒性进行处理后,对测量值进行如下更新:

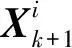
1.2.2 自适应信息共享系数

在实际应用中,考虑到不同子滤波器的过滤精度不一致,需要根据过滤精度调整每个子滤波器分配信息的比例[28]。本文子滤波器的精度λi(k)如下:

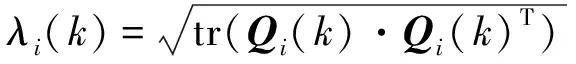
(13)

式中:λi(k)为子滤波器的精度;Qi(k)为状态协方差矩阵;tr(·)是矩阵的迹。

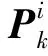
(14)

假设信息共享系数满足如下关系:

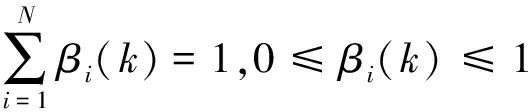
(15)

式中:βi(k)为信息共享系数。

主滤波器不分配信息,因此自适应信息共享系数表示为:

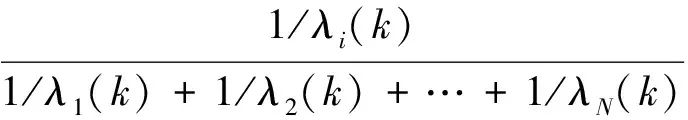
i=1,2,…,N

(16)

1.2.3 鲁棒自适应多源模型

如图2所示,本文利用IMU/GNSS/VO构建多源融合导航系统。对IMU/GNSS和IMU/VO分别进行鲁棒滤波,并通过鲁棒等效权值自适应调整信息共享系数。

图2 鲁棒自适应多源模型Fig.2 Robust adaptive multi-source model

2 输电线跟踪算法

在图像处理过程中,首先通过前一帧中的滑动线模型来剪切输入图像。选择感兴趣区域(region of interest, ROI)进一步分析和跟踪电力线。正确的ROI标识可以减少后期的搜索空间。对于初始帧,假设电力线模型由用户给出。

然后从ROI中裁剪出一组补丁{P1,P2,…,Pn}进行下一步处理。

Pi={(u,v)∣(u,v)∈ROI,l1≤v≤l2}

(17)

式中:u、v分别为二维离散空间坐标;ROI为前边所述的ROI;l1、l2为两条线。然后,将现有的目标(补丁)检测算法,如文献[16]中给出的算法,应用于所有补丁。对于找到的任何补丁,提取其方向信息。

接下来,对Canny方法中的边缘检测内核(在第2.2节中讨论)和滞后阈值进行改进(在第2.3节中讨论)。在航空拍摄的图像中,从不同方向观看时,相同背景的最佳边缘检测参数几乎相同。根据这一观察,假设最佳参数是在W空间中(x,y,z)的函数。然后,将图像中的每个点映射到相应的物理空间(映射函数在第2.1节中给出)。通过该映射,无人机可以获得所有补丁的相关坐标。当无人机飞行时,建立并保存最佳参数数据库。对于每个传入图像,如果在数据库中找到与其关联的GPS坐标,则将补丁分类为正;否则,它被归类为负。对于正补丁,使用数据库中的最佳参数进行边缘检测。对于负补丁,基于电力线模型预测最佳参数并将其存储到数据库中。

接下来,使用约束霍夫变换来过滤不相关的线性结构(见第2.4节)。然后,基于在所有补丁中检测到的电力线和补丁重建新的电力线模型。然后,进入下一帧。

2.1 输电线图像映射

在I空间中,所有电力线有可能汇聚到一点,成为消失点(vanished point, VP)。所有可能电力线的函数由式(18)表示。

v-vp=m(u-up)

(18)

式中:(u,v)为电力线坐标;(up,vp)是VP在I空间中的坐标;m是斜率。

此外,假设电力线与其他电力线平行,并相隔一段距离Dij=(xi-xj),其中xi是W空间中x轴上第i条输电线坐标。因此,在I空间中,点p(ui,v)和p(uj,v)之间的水平距离为:

(19)

式中:f为镜头焦距;p(ui,v)和p(uj,v)两个点为输电线投影点;zc为距离参数。基于式(18)、(19)设计边缘检测器和线检测器。

2.2 边缘检测器内核设计

一般边缘检测方法中使用的算子增强了线性对象(例如输电线)和强对比区域的边缘,这可能对电力线检测产生负面影响。设计了一个一维核来代替Canny边缘检测中的Sobel核。在I空间中,电源线在图像上具有不同的厚度。通过将输电线电缆的直径d代入式(20),可得I空间中的电力线厚度:

(20)

式中:n为无人机相机分辨率。

由式(20)可知,核的宽度仅由I空间中的v坐标确定。通过在垂直和水平维度上卷积核,得到了两个方向上的边缘强度。

图3显示了可变长度内核丢弃了大多数杂波(深色线性对象和强对比区域之间的边缘),并且仅对明亮的线性特征有强烈的响应。

图3 一维核结果Fig.3 Results of the one-dimensional kernel

2.3 边缘检测参数获取

导出图像的强度梯度后,执行普通边缘细化(与Canny相同)。本文开发了一种最优参数获取方法,如图4所示。通过使用电力线模型,在滞后阈值步骤中选择两个阈值。

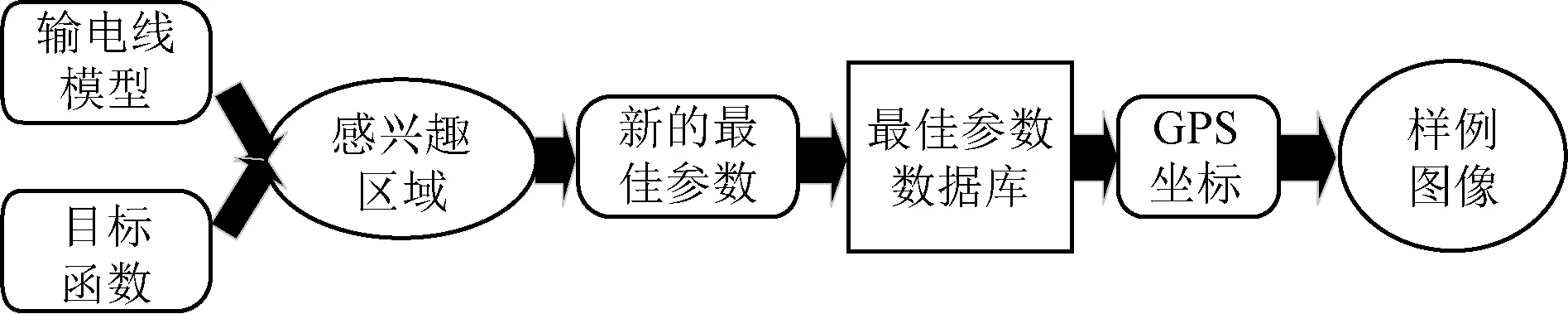
图4 参数获取过程Fig.4 Parameter acquisition process

对于式(17)中的每个Pi,其在空间W上的对应区域为:

Si={(x(u,v),y(u,v),z(u,v))∣(u,v)∈Pi}

(21)

式中:x、y、z为W空间物理坐标。

在本文中,无人机为所访问的地点保存一个最佳参数数据库。对于正补丁,无人机将根据其相关GPS坐标检索其最佳参数。对于负补丁,使用目标函数和电力线模型来预测最佳参数。在给出目标函数之前,首先对边缘像素进行分类,如果满足式(22),则将边缘像素e分类为信号像素,否则将其分类为噪声像素。

minl∈L{d(e,l)}≤dmin

(22)

式中:L是前一帧检测到的电力线集合;d(e,l)为返回边缘像素e与输电线l之间的距离;dmin是像素为信号像素的最小距离。目标函数如下:

(23)

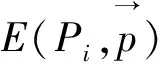
(24)

式中:argmin()代表取值最小函数。

2.4 约束霍夫输电线检测

霍夫变换用于通过将所有边缘像素映射到参数空间来检测线。通过选择空间中的峰值来检测输电线。霍夫变换在线路检测方面性能强大,但它不能从其他线性结构中智能地识别电力线。为了解决这个问题,本文使用电力线在约束霍夫空间中的高层空间信息来过滤不相关的线性结构。

一条直线y=ax+b在参数空间可被描述为(r,θ),r是原点到直线上最近距离,θ是x轴和直线之间的角度。(r,θ)可以用式(25)表示。

(25)

图5给出了参数空间中不同VP的所有可能峰值。在本文的约束霍夫线检测中,只搜索曲线附近的空间。这种方法在本文实验中被证明是有效的,因为在连续帧中检测到的相同电力线的差异非常小。

图5 约束霍夫空间Fig.5 Constrained Hough space

3 实验与分析

本文利用鲁棒自适应定位算法对位置和安全距离等信息进行快速收集和研判;同时通过鲁棒自适应联合卡尔曼滤波(robust adaptive federated Kalman filtering, RAFKF)跟踪算法来解决定位识别时间较长、实时性较差的问题。并且自主巡检通过对同一位置的多次复拍,形成杆塔图像库,可进行历史图像对比,更好地了解设备变化,了解设备隐患形成的时间点和形成原因,更好地帮助巡检人员制定检修方案。

3.1 模拟设置

模拟建立的初始位置(局部坐标)为[0 m; 0 m; 0 m],初始姿态(俯仰,翻滚,偏航)为[0; 0; 0],初始速度为[0 m/s; 0 m/s; 0 m/s]。

本文设计了三种方案来模拟无人机的轨迹:

方案1：传统的联邦卡尔曼滤波,信息共享系数均匀分布。

方案2：自适应联邦卡尔曼滤波,子滤波器保持不变,主滤波器根据子滤波器的精度自适应调整信息共享系数。

方案3：鲁棒自适应联邦卡尔曼滤波,子滤波器进行鲁棒滤波,主滤波器根据子滤波器的精度自适应调整信息共享系数。

表1为各传感器(IMU、GNSS、VO)的测量误差参数及更新频率。

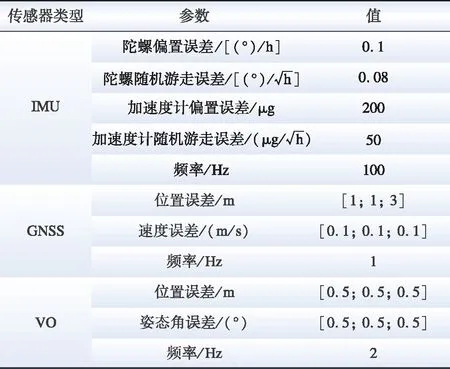
表1 传感器参数Table 1 Sensor parameter

3.2 定位精度分析

3.2.1 不同组合系统状态估计比较

图6为不同组合系统状态估迹轨迹。图6中,星号表示起始位置,虚线表示放大区域的位置。黑线为真实轨迹,红线为VO/IMU估测轨迹,绿线为GNSS/IMU估测轨迹,蓝线为VO/GNSS/IMU估测轨迹。如果使用三个子滤波器进行独立导航,由于不同时间段的观测值存在较大误差,会导致状态估计精度降低,从而偏离真实轨迹。正如预期的那样,VO/GNSS/IMU的全局最优融合性能可以不受局部传感器给出异常信号的影响,精度较高。

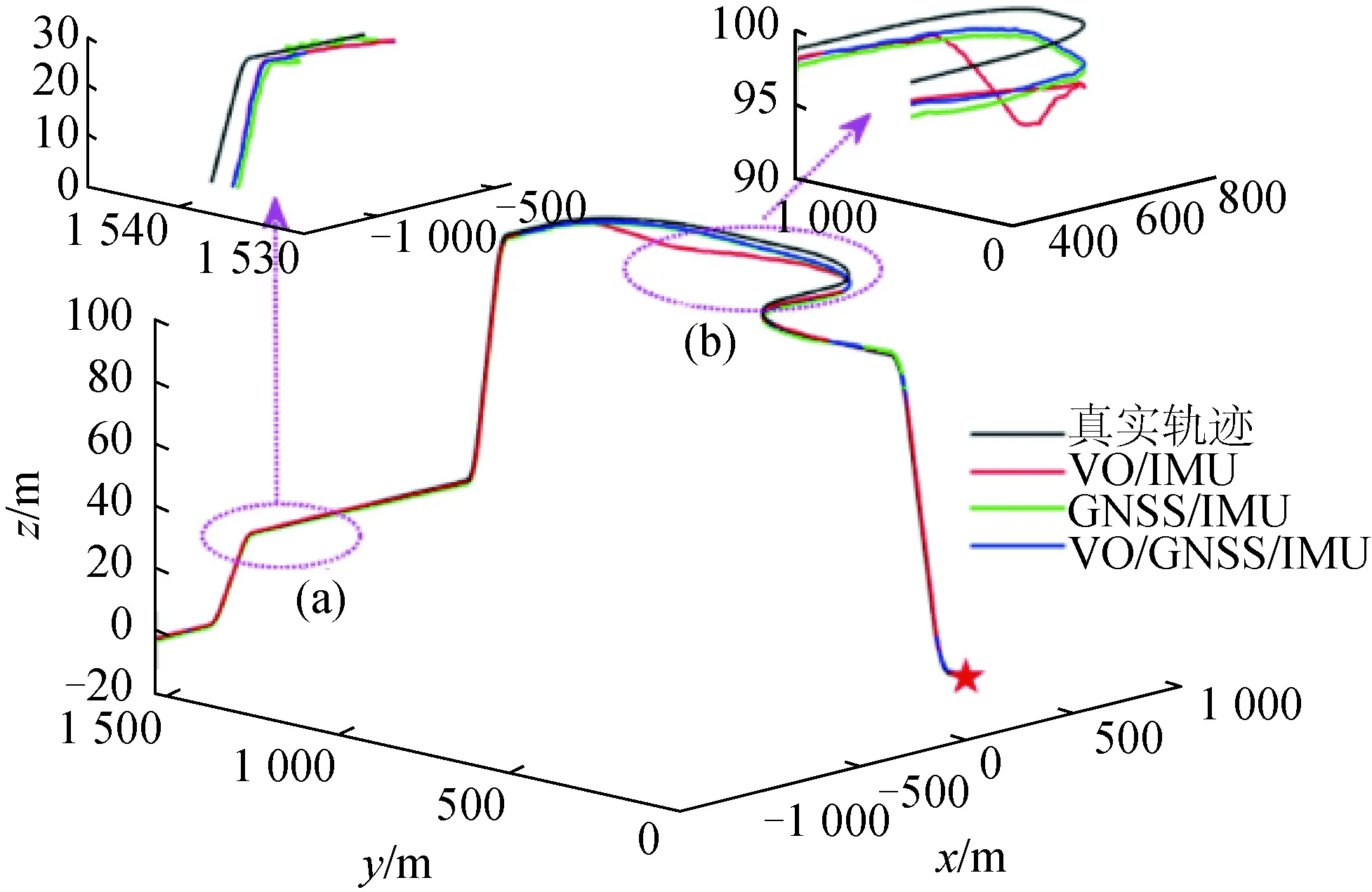
图6 不同组合系统状态估计比较Fig.6 Comparison of system state estimates for different combinations

3.2.2 不同方案结果比较

不同方案对比结果如7—10所示。图7中,黑线为真实轨迹,红线、绿线、蓝线分别表示方案1、2、3轨迹。由图7可以看出,这三种滤波方法都可以用于VO/GNSS/IMU系统定位。由图8—10可知,从整体上看,特别是在100～200 s和270～370 s期间,与自适应联邦卡尔曼滤波和联邦卡尔曼滤波的估计轨迹相比,鲁棒自适应联邦滤波估计轨迹最靠近实际值。

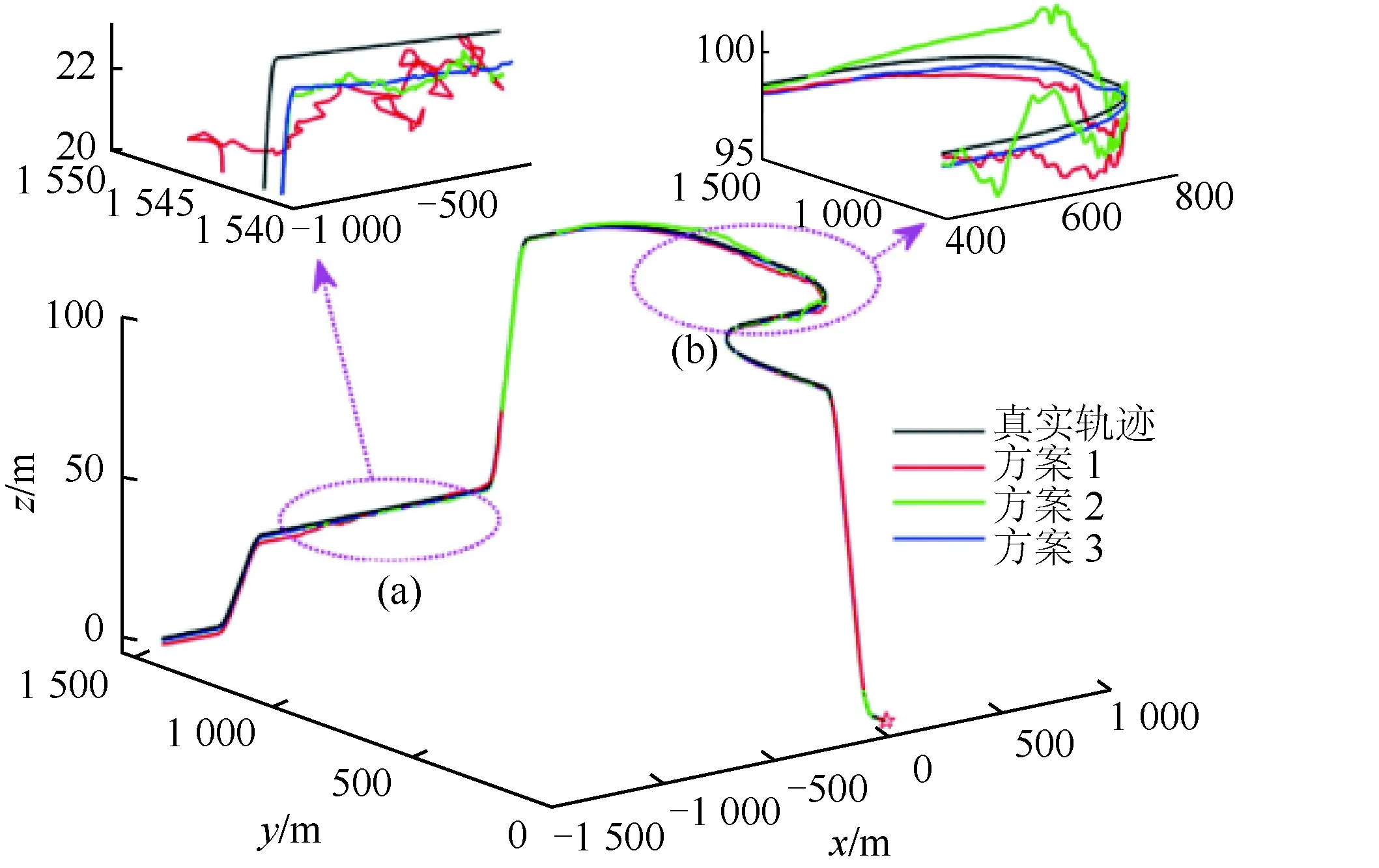
图7 不同方案的轨迹比较Fig.7 Trajectory comparison of different schemes

图8 姿态误差比较Fig.8 Comparison of attitude errors

三种方法的姿态角估计都能跟踪真姿态角的变化,但精度不同。可看出方案3的精度优于另外两种方案。

图9和图10为速度和位置误差对比结果。可看出方案3整体误差比较稳定,在零值附近有轻微的振荡。在本文设定的两个时间段内,即使局部传感器受到干扰或完全失效,整个系统仍能保持足够高的导航精度。这是因为方案3在本地传感器受到外部干扰影响时,可以及时在不同系统之间切换以重新分配权重。因此,鲁棒自适应滤波器可以掌握每个局部系统当前的自适应状态,并能有效地利用状态精度更高的子滤波器,从而减小误差。

图10 位置误差比较Fig.10 Comparison of position errors

无人机巡检输电线路时可能遭遇大风导致抖动、空气能见度低导致观察效果差、地形以及遮挡物干扰等复杂情况。为了验证所提方法在复杂工况下的工作效果,本文进行了20次模拟真实环境的蒙特卡洛模拟实验来进一步比较三种信息融合方案,如表2所示,每组噪音、轨迹和速度都不同。

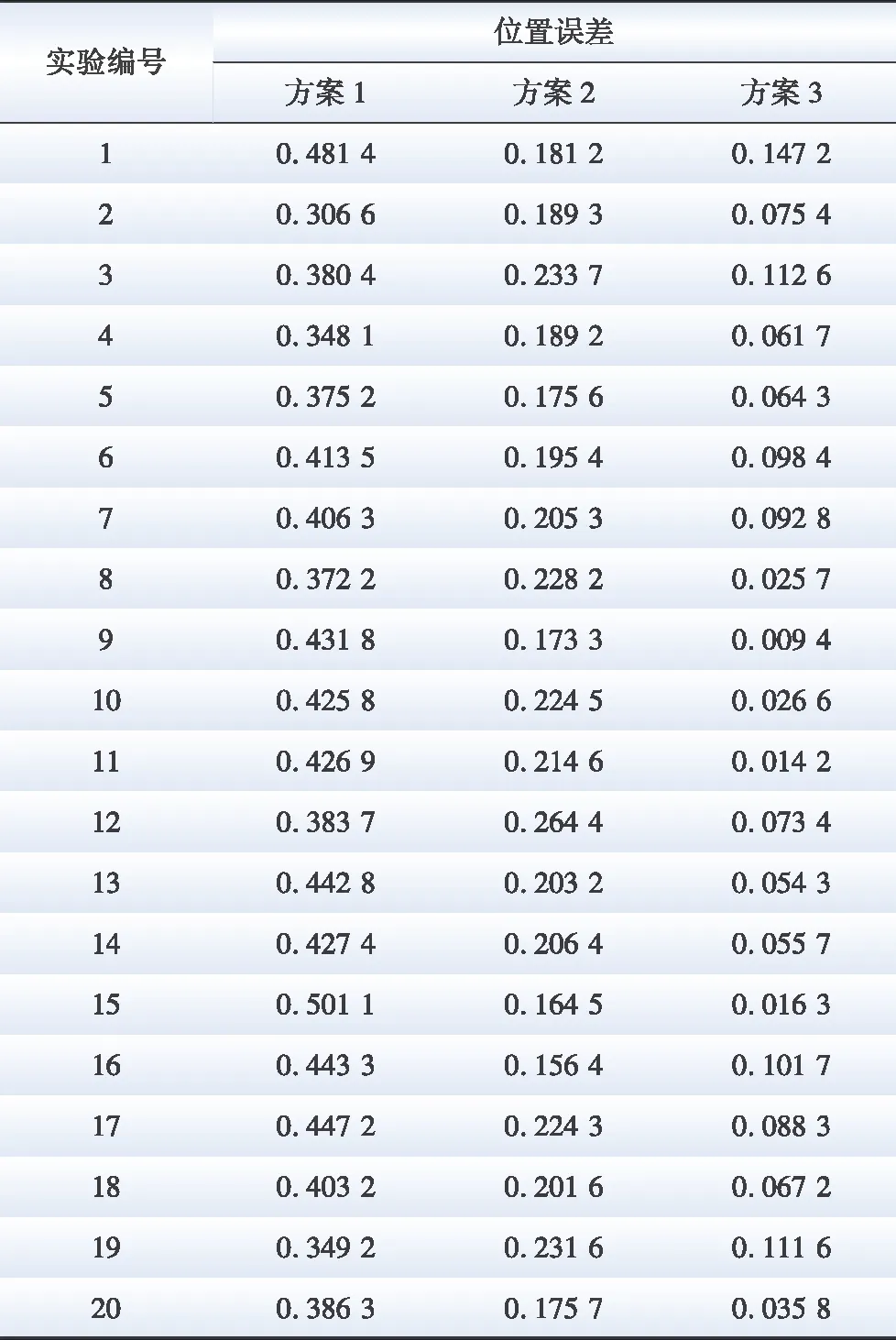
表2 20个实验组的位置误差Table 2 Position error for 20 experimental groups m

如表2所示,方案3(鲁棒自适应联邦卡尔曼滤波)的精度明显优于其他两种方案。分别计算20个实验组的平均位置误差精度,得到三种方案的误差分别为0.401 0 m、0.2117 m、0.071 9 m。与方案2相比,方案3的准确率提高了66%,与方案1相比提高了82%。这是因为鲁棒自适应联邦卡尔曼可以对子滤波器估计值进行鲁棒自适应调整,主滤波器根据子滤波器估计值权重进行自适应信息共享系数分配。主全局最优融合滤波器的性能受局部传感器异常影响较小,可以达到较高的巡检精度。上述结果讨论和分析进一步证明,本文提出的鲁棒自适应联邦卡尔曼滤波算法具有较高的精度和良好的鲁棒性,并可适用于复杂环境。

3.3 输电线检测与跟踪分析

基于唐山地区真实环境(见图11)测试本文提出的输电线检测与跟踪算法。图11(a)显示了测试环境的航空地图。在环境相对简单的区域,自动跟踪的电力线标记为绿色,在环境复杂且有大量人工结构的区域,标记为红色。无人机在典型故障情况下的图像如图11(b)所示,无人机的位置用红色标记。故障的常见原因是摄像机捕捉到的属于不同电源线组的其他电线杆。本文方法不能很好地处理这种交叉点,因此,无人机随机选择其中一条电源线,而不是跟随原电源线。

图11 测试环境航拍图Fig.11 Aerial photograph of the test environment

图12—14给出了不同方法线检测结果。图12(a)的原始图像显示了复杂背景的场景之一。图12(b)和图13是本文方法和Canny边缘图上的霍夫变换结果。图12(c)和图14是本文方法和Canny边缘图上的约束霍夫变换结果。从结果来看,本文方法(图12(b)、(c))比手动调整的最佳Canny和霍夫变换结果(图13、14)具有更好的性能。在相同的参数下,改进的边缘检测内核(图12(c))优于Sobel内核(图14(c))。