基于可解释性XGBoost的电力系统惯量短期预测方法

张磊,李海涛,熊致知,郭志豪, 叶婧, 李振华, 杨楠, 蔡煜

(1. 三峡大学电气与新能源学院, 湖北省宜昌市 443002;2．新能源微电网湖北省协同创新中心, 湖北省宜昌市 443002;3．国网华中分部调度控制中心, 武汉市 430077)

0 引 言

随着我国电力系统转型升级,以新能源为主体的新型电力系统中同步机逐步被取代,系统惯量随之减少[1]。多起系统频率安全事故表明,系统运行在惯量薄弱场景下的切负荷风险增大,未提前掌握系统真实惯量水平给电网安全稳定运行带来了重大挑战[2-3]。因此,快速、准确地预测电力系统短期惯量,提前预警系统何时面临惯量薄弱的风险,对电网调度部门制定相应的控制措施具有重要意义。

目前,电力系统惯量短期预测方法的研究主要有统计学方法和机器学习方法。统计学方法主要有回归分析法[4]、差分自回归移动平均模型[5]、最小方差有限脉冲响应滤波器[6]、贝叶斯模型[7]等。基于统计学方法的预测需假定系统惯量仅由同步发电机产生,忽略系统其他潜在的惯量来源。该方法缺少对新型电力系统中其他复杂非线性虚拟惯量的表征,阻碍了其在系统惯量短期预测上的应用[8]。然而,机器学习方法可以避免对电网复杂特性的分析和高维非线性公式推导[9],文献[10]基于人工神经网络开发了预测电力系统惯量工具,通过广域测量管理系统(wide area management system,WAMS)量测数据训练预测模型,预测精度高且计算速度快。

然而,机器学习模型的预测过程类似于“黑箱”,模型缺乏可解释性,其结果难以为电网调度部门的具体决策提供相关解释性信息,成为机器学习方法在系统惯量短期预测应用中的主要问题。可解释性研究作为一种能够挖掘出特征相关性和阐明机器学习模型决策过程的方法[11],可为调度人员提供可理解的结果。在可解释性研究中,建立自身可解释机器学习模型是一种简单有效的方法,如:线性模型利用特征线性拟合来解释模型局部空间中的运算逻辑[12],决策树基于决策路径提取可解释规则[13]。但是对于系统惯量短期预测的大规模数据问题,准确预测需建立复杂模型,复杂程度高意味着解释性低,而模型自身可解释性的提升往往以牺牲预测精度为代价,预测精度难以与可解释性相平衡。近年来的研究将解释与机器学习模型分离,其可解释性方法包括全局代理模型[14]、局部代理模型(local interpretable model-agnostic explanations,LIME)[15]等,运用可解释的代理模型描述机器学习模型的预测过程,并给出可理解的结果。这类方法在保证较高准确率的同时可以掌握模型内部的特征相关性,已应用于生物医疗预测[16]、金融预测[17]、计算机视觉[18]等领域,但在电力工业领域的预测研究中鲜有应用。

基于上述分析,本文提出了基于可解释性极端梯度提升算法 (extreme gradient boosting,XGBoost)的电力系统惯量短期预测方法。首先,利用SHAP(Shapely additive explanations)方法构造XGBoost机器学习模型的解释机制,构建可解释性XGBoost。选取电力系统运行数据和气象数据作为输入,系统惯量作为输出,训练系统惯量短期预测模型。最后通过实际系统验证文中方法的有效性,挖掘出影响系统惯量短期预测的特征相关性,从全局和局部层面阐明机器学习模型的决策过程。

1 可解释性XGBoost算法

机器学习模型在提升预测能力的过程中,牺牲了模型的解释性能力,随着模型的复杂程度增加,其预测过程难以被直观地表述,这成为实际工程应用的主要阻碍因素。因此,为解决模型可解释性不佳的问题,有必要对其进行可解释性分析。

1.1 Boost算法

XGBoost是一种Boosting的集成学习模型,采用决策树(classification and regression tree,CART)作为基学习器,集成为一个强学习器[19]。XGBoost模型表示为:

(1)

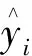
(2)

(3)

式中:yi为第i个样本输出;l(·)为损失函数,是预测值和实际值之间的误差,Ω(·)为正则化项,防止过拟合;T是叶子节点的数目;ωj是叶子节点的权重;γ和λ是预先给定的超参数,分别用于控制叶子节点的个数和分数。

利用增量训练的方式以最小化目标函数,在第t轮迭代时添加ft,更新目标函数为:

(4)

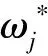
(5)

(6)

式中:Gj是叶子节点j所包含样本的一阶偏导数的累加之和,见式(7);Hj是叶子节点j所包含样本的二阶偏导数的累加之和,见式(8)。

(7)

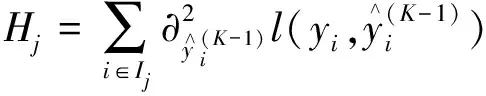
(8)

式中:Ij是节点j的样本集;∂是偏导数符号。

训练过程中,XGBoost生成树模型的分裂准则采用贪心算法,选取使目标函数的增益Gain最大的特征节点为分裂点。利用增益提取特征的重要程度,即某特征被选为分裂节点的次数越多,则该特征的重要性就相对越高[20]。从树的根节点开始计算Gain,表示如下:

(9)

式中:GL、HL、GR、HR分别为分裂时当前节点左右子树的一阶、二阶导数和。

XGBoost算法不能满足衡量特征影响方向和影响程度的评判,对于单个样本的特征与系统惯量映射关系也无法解释,因此有必要对其预测结果进行可解释性分析。

1.2 基于SHAP的XGBoost解释

以往的研究者只能通过类似于特征重要性的方法,判断模型选出的重要变量是否符合预期,以此在一定程度上把控模型的效果[21-22]。但模型如何作出相应的判断,关系到模型预测结果是否可信。

SHAP是一种解释黑箱模型的特征归因方法[23]。针对XGBooost模型的黑箱结构构建解释机制,通过sigmoid函数将模型预测值与SHAP解释模型g(x′)相关联,构建可解释性XGBoost如下:

(10)

基于合作博弈论理论计算的Shapley值,SHAP解释模型描述为模型对于样本的预测基准值φ0与所有输入特征Shapley值之和的形式:

(11)

(12)

式中:φj是样本第j个特征的Shapley值;m是样本的特征数目;x′j∈{0,1}m表示特征xj是否存在;z是样本的全体特征向量的集合,z⊆{x1,x2,…,xm};zj是z中不含特征xj的特征子集;Fx(z)是XGBooost模型对于样本x输入特征为z时得到的预测输出;Fx(z)与Fx(zi)之差为特征xj对预测结果的贡献。

基于SHAP归因方法构建的可解释性XGBoost满足局部精确性、允许缺失和一致性的特性。所有特征重要性的和等于模型的总体重要性,局部精确性解释了模型对单个样本的预测结果。允许缺失性表示样本的特征对模型的预测没有贡献时,XGBoost不对变量进行插补处理。当更改模型以使其更多依赖于某个特征时,该特征的重要性不降低,此时输入特征的边际贡献与输入特征的Shapley值变化一致。SHAP的一致性由Shapley值自身的可加性、虚拟性和对称性的性质得到。SHAP是唯一同时满足上述特性的归因方法,基于合作博弈论的理论基础,公平计算各项特征的Shapley值,保证解释的合理性。

可解释性XGBoost算法流程如图1所示,从全局和局部两个维度对模型进行解释分析,表示为:

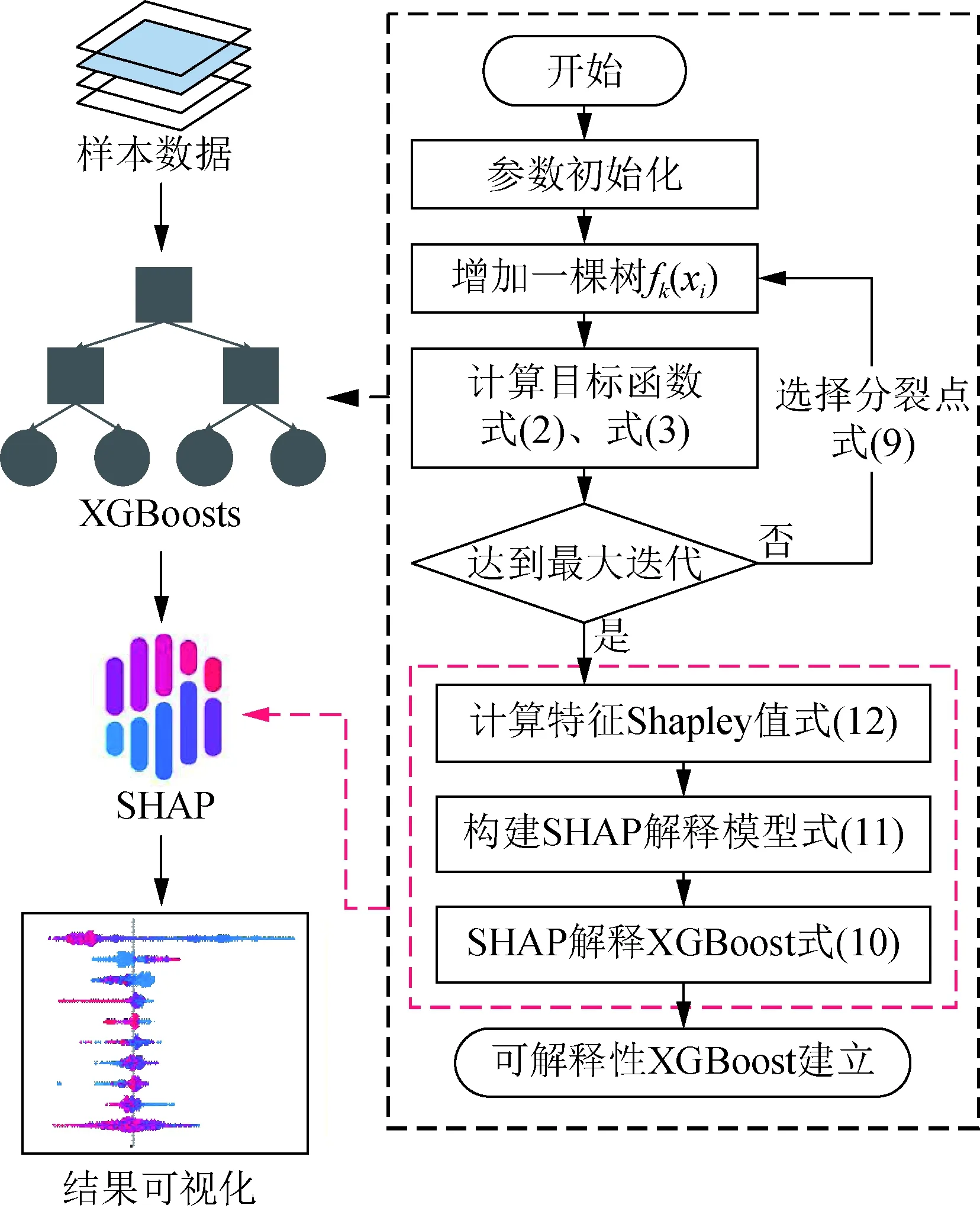
图1 可解释性XGBoost算法流程Fig.1 Interpretable XGBoost algorithm process

1)全局可解释性:解释模型如何基于整个特征空间和模型结构、参数等做出决策。从全体样本的角度考虑,据式(12)得到全部特征的Shapley值,对样本集合中每项特征的Shapley值求平均绝对值。值的大小反映特征对模型输出结果的全局贡献程度,此外,根据每个特征的Shapley值与特征自身数值的分布关系,挖掘特征数值与模型输出的正负相关性。

2)局部可解释性:解释所有特征如何对单个样本的输出结果做出决策,不考虑整个模型的复杂情况,只关注于单个样本。将单个样本的输出表示为式(11)各项特征的Shapley值之和的形式,进而确定该样本的局部主导特征。结合全局可解释性分析,明确特征对样本输出结果的偏高或偏低影响。

与传统XGBoost计算特征重要性方法相比,可解释性XGBoost能拆解并定量映射为各个特征对模型预测结果的贡献,意味着找出影响系统惯量预测的关键因素,阐明XGBoost模型的决策过程,从而解决XGBoost模型可解释性不佳的问题,提高预测结果的可信度。

2 电力系统惯量短期预测模型

2.1 问题描述

电力系统惯量短期预测是一个高维的回归分析问题。样本数据集描述如式(13)—(14)所示,输入样本集每一行与输出样本集相对应:

(13)

Y=[y1,y2,…,yn]T

(14)

式中:X是输入样本数据集;Y是输出样本数据集;上标m是输入特征的维度;下标n是输入样本的数目。其中,X的每一行表示一个输入样本。

基于可解释性XGBoost预测的电力系统惯量值的问题,可以描述为多输入与单输出间模型求解和解释的问题。将输入特征变量和系统惯量数据分别作为模型的输入和输出,采用并行方式训练多个可解释性XGBoost模型可以表示为:

(15)

2.2 输入特征选择

输入特征选取的原则是:一方面能很好反映系统惯量特性,另一方面计算要保证时间上的快速性。文献[3]给出系统惯量的概念:在系统受到扰动时,电力系统惯量迅速响应以分担扰动功率,维持系统频率稳定而不解列崩溃。为保证电力系统惯量预测的准确性,依据系统有功-频率动态变化中电力系统惯量响应方程[24],选取合适的特征。

(16)

式中:Hsys和Dsys分别为系统惯量和系统阻尼;ΔP是系统功率变化率;ΔfCOI是惯量中心频率偏差。

由式(16)知,影响系统惯性的因素有频率和各类能源的有功功率。考虑系统频率、负荷需求对系统惯量的影响,文献[25-26]明确了需求侧负荷对系统惯量的贡献,其惯量体现在负荷需求对频率变化的响应。因此,输入特征选取应考虑系统频率和负荷需求。

从电力系统惯量的组成来看,系统惯量包括传统能源(煤炭、石油、天然气、化学能、核燃料等)通过同步机旋转产生的转动惯量和新能源(太阳能、风能、生物质能、地热能、潮汐能等)/储能通过虚拟惯量控制策略提供的虚拟惯量,因此选取传统能源和常见的新能源的有功出力作为输入特征。同时,新能源出力受气象因素显著影响,极端天气如冬季寒潮、暴雪等事件对电力系统有较为严重的影响,在诸多气象数据中捕获异常信息是系统惯量预测的关键[27],因此,选择基于数值天气预报(numerical weather prediction,NWP)的气象数据作为输入特征。

在特征数据采集过程中难以避免存在缺失值、异常值等噪声数据。在使用之前需要进行数据预处理,对数据集进行数据清洗和填充,缺失值可以直接通过数值运算进行填充,若检测出异常值则用均值代替异常样本[28]。

2.3 预测评价指标

预测结果的评价指标使用平均绝对误差(mean absolute error,MAE)、均方误差(mean squared error,MSE)、平均绝对百分比误差(mean absolute percentage error,MAPE)和决定系数(coefficient of determination,R2):

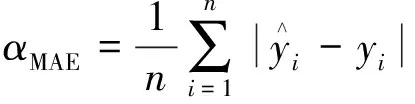
(17)

(18)

(19)

(20)

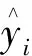
2.4 预测流程

基于可解释性XGBoost进行系统惯量短期预测的流程如图2所示,其过程包括数据预处理、模型训练、结果输出,具体为:

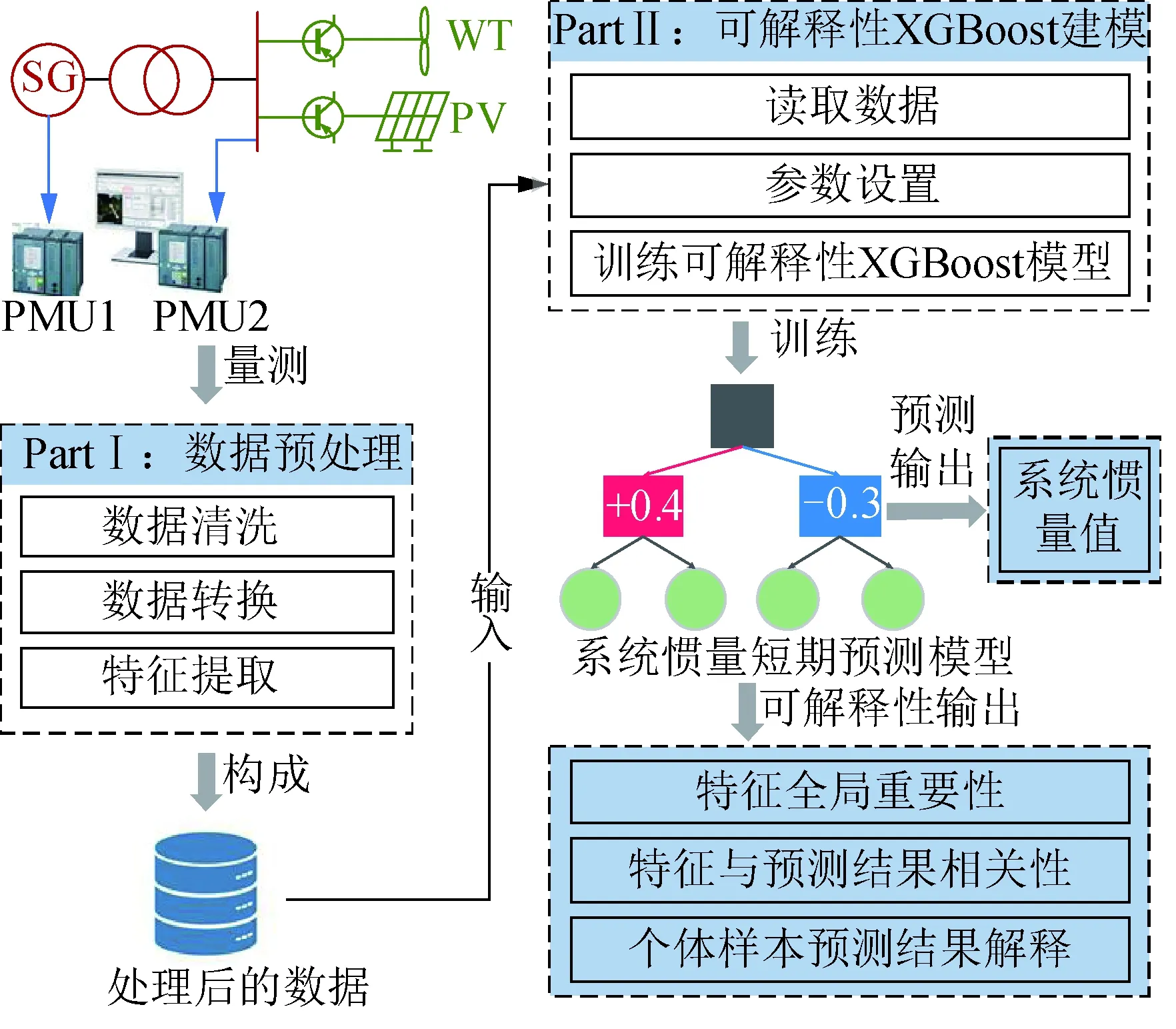
图2 电力系统惯量短期预测框架Fig.2 Short-term prediction framework for power system inertia

1)数据预处理:基于WAMS采集的历史数据,提取影响系统惯量预测的相关物理量作为输入特征,经预处理得到可供模型训练的数据集。

2)模型训练:将数据集划分为训练集与测试集,训练集用于训练可解释性XGBoost模型,测试集用于模型评价及结果验证。

3)结果输出:对输出系统惯量值和特征相关性进行分析,并可视化展示特征对电力系统惯量短期预测模型的全局和局部影响。

3 算例分析

3.1 实验环境

为验证所提方法的有效性,以英国电网为研究对象进行系统惯量短期预测,仿真软件Python的版本为3.7.6,其中Scikit-learn版本为0.19.0。选择英国电力结算中心(ELEXON)提供的英国国家电网2020年1月1日至2020年12月31日的实测数据[29-31],数据的采样周期为5 min,每天产生288组数据。输入特征选择气象特征、常规机组及新能源功率、频率和负荷需求等,收集到28维输入特征如表1所示。

表1 系统惯量预测的输入特征集Table 1 Input features for system inertia prediction

在进行可解释XGBoost模型训练时,从英国电网实测数据中选择2020年12月22日至2020年12月27日共1 728组数据作为训练数据,以2020年12月28日至2020年12月30日的数据为测试数据,预测2020年12月31日的短期电力系统惯量,并与实际值进行对比。

3.2 模型预测精度效果

将本文所提方法与其他6种主流机器学习算法进行对比,并使用MAE指标、MSE指标、MAPE指标、R2指标4个指标进行模型评估,主流机器学习算法预测模型均基于Scikit-learn平台搭建且使用默认参数,各模型的计算结果如表2所示。

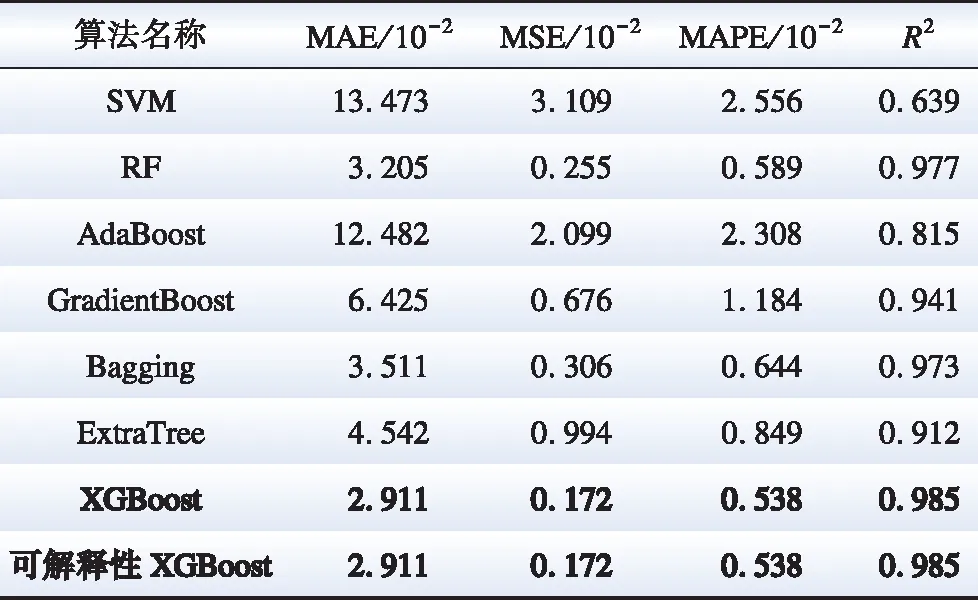
表2 与主流机器学习算法误差结果对比Table 2 Comparison with error results of mainstream machine learning algorithms

结果表明,基于SHAP的可解释性XGBoost算法与XGBoost算法精度在测试数据上预测精度最高,R2为0.985意味着它可以正确预测电力系统惯量短期的变化趋势,预测结果如图3所示。可解释性XGBoost算法在保证模型预测准确率的同时,提高了预测结果的可信度。SVM的结构简单,在处理复杂高维问题时易欠拟合,导致预测效果不佳。虽然RF的树模型预测效果较好,但仅适用于当前训练集,在训练集数据范围外的预测易出现过拟合,阻碍了该方法进一步预测系统惯量值。

在集成算法中,GradientBoost、Bagging和ExtraTree的R2评价均高于0.90,而AdaBoost仅为0.815。AdaBoost算法的其他各项评价指标与集成算法均不在一个数量级,正如表2所示。使用可解释性XGBoost算法的平均绝对误差为2.911%,均方误差为0.172%,平均绝对百分比误差为0.538%,预测结果优于其他机器学习模型。因此,相比于其他类型的算法,可解释性XGBoost可以有效预测系统短期惯量。

3.3 模型预测结果的全局可解释性

根据特征重要性对影响系统惯量的因素进行排序,得到基于SHAP的可解释性XGBoost模型的特征重要性,如图4所示。图中的点代表每一个样本,横坐标为特征的Shapley值,将每个特征的Shapley值分布情况与用不同颜色代表的特征值大小关联起来,样本点颜色越红表示该特征本身的Shapley值越大,从而根据特征的颜色分布情况判断出特征对模型的影响效果。纵轴为特征的特征值,28维特征按重要性从高到低依次排列,特征值越大其重要性越高。

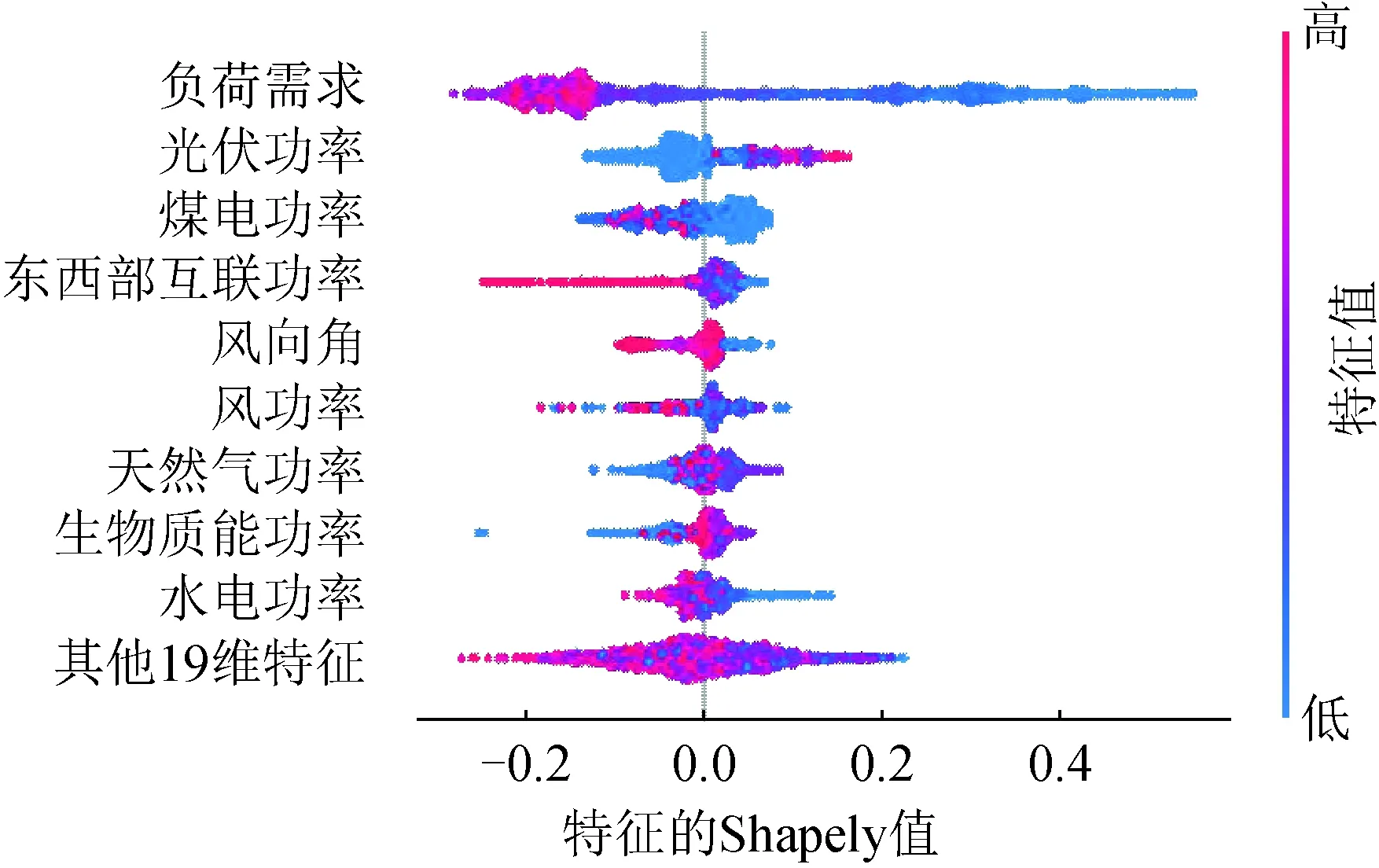
图4 特征重要性Fig.4 Feature importance

从图4可以看出,对于电力系统惯量预测模型而言,最重要的是负荷需求、光伏功率和煤电功率等特征。其中,负荷需求的特征值最大,数值分布方差显著高于其他特征,Shapley值大量聚集在平均值以下。蓝色表示负荷需求较小,此时对模型预测结果带来正向的影响,反之红色表示负荷需求较大,给预测结果带来负向影响。该颜色分布表明,负荷需求越高,系统惯量值越大,这与电力系统实际运行的认知一致。

以负荷需求和光伏功率特征为例,图5和图6进一步展示各自Shapley值与特征自身数值的关系。特征的Shapley值大于0时,说明随着特征值的增加对模型系统惯量预测在数值上呈现增大的趋势,Shapley值小于0时在数值上呈现减少的预测趋势。

图6 光伏功率特征Shapley值Fig.6 Photovoltaic power characteristic Shapley value

可以发现,负荷需求小于35 000 MW时,负荷需求的Shapley值与其特征值是负相关,直至负荷需求大于35 000 MW时,Shapley值稳定在-0.2附近。从物理意义的角度看,负荷需求增加系统惯量呈增加趋势,说明更多的同步机组被启动,但当负荷需求进一步增加,瞬间的功率缺口给电网运行带来负担,系统可能面临惯量薄弱的风险。对于光伏功率而言,图6中光伏出力为0时Shapley值小于0,此时预测系统惯量值更可能低于基准值,说明光伏资源匮乏时,等效的系统惯量呈减少趋势。

上述两个特征的SHAP分析结论与系统运行的规律是一致的,表明模型解释结果符合客观物理规律。基于解释分析特征对模型决策过程的影响,可以加强调度部门对模型的理解和信心。

3.4 模型预测结果的局部可解释性

选择2020年12月31日0点和12点的样本进行局部可解释性分析,对单个样本的预测解释有助于理解输入特征如何进行预测。两个时刻的预测结果分别是图7和图8,各特征的Shapley值之和加上样本基准值就是模型的输出结果,即该时刻的系统惯量值,各特征Shapley值见附录表A1。对同一个特征在不同样本间的Shapley值进行对比分析,图中红色的特征表示其Shapley值为正,会给预测值带来正向的贡献,即增大系统惯量的预测值,且色块的面积越大意味着对模型输出结果的影响越大,反之面积越小则影响越小。

图7 2020年12月31日0点系统惯量预测结果Fig.7 Prediction result of system inertia at 00:00 on December 31, 2020

图8 2020年12月31日12点系统惯量预测结果Fig.8 Prediction result of system inertia at 12:00 on December 31, 2020

附录A

0点负荷需求带来的正向影响最大,光伏功率带来的负向影响最大,模型预测的输出结果为5.559高于预测基准值5.378,此时系统惯量不处薄弱状态。12点光伏功率带来的正向影响最大,负荷需求带来的负向影响最大,12点模型预测输出结果低于预测基准值。12点时,若光伏功率特征的负向影响急剧增大,则系统惯量有进一步下降的趋势,系统发生切负荷/切机的风险增大。因此,调度部门应重点关注该时刻下光伏出力情况。

结合图5所反映的特征正负相关性进一步分析,0点的负荷需求较35 000 MW低出7 292 MW,使模型对相应样本预测惯量值增加了0.160,12点则高出2 190 MW使预测惯量值减少了0.142。在不同样本个体中,特征对于模型决策影响存在差异,但负荷需求和光伏特征等全局重要性较高的特征对不同样本个体的预测结果影响均较大,与图4结论一致。依此类推,可以对每个样本都生成具体细致的分析,全面的数据信息能够协助调度部门更好地制定决策。

可解释性XGBoost基于博弈论的理论基础,从全局和局部两个维度将黑箱结构进行解构,保证解释的合理性。以一致性的方式准确地表征特征对惯量预测结果的影响,挖掘出特征相关性,并阐明模型决策的过程,加深了对整个模型的感知和对每次预测成因的理解,使得模型预测过程更加透明,提高了系统惯量短期预测模型输出结果的可信度。

4 结 论

本文提出了可解释性XGBoost的电力系统短期惯量预测方法,利用实际电网数据验证了方法的有效性,得出以下结论:

1)基于可解释性XGBoost算法,利用电力系统运行数据和气象数据构建特征,建立了电力系统短期惯量预测模型。结果表明该模型可以有效预测系统短期惯量。

2)可解释性XGBoost以一致的方式量化特征对系统惯量短期预测的影响。全局可解释性挖掘了影响系统惯量的关键物理量,局部可解释性对每次预测结果进行因果判断,提高了预测结果的可信度。

3)准确预测系统短期惯量并提供可理解的结果,可为电网调度部门预防潜在的不稳定风险和制订紧急控制策略方案提供参考。

当前研究虽然可以有效预测系统的短期惯量,但所选取的特征局限于英国电网。如何选取普遍适用的特征信息实现系统惯量短期预测,并研究消除电力系统惯量薄弱风险的措施,是下一步研究工作的重点。