深部低品位资源阶段空场嗣后充填采矿法采场结构优化与稳定性控制

孙星　安龙

摘要：基于阶段空场嗣后充填采矿法采场围岩稳定性控制难题，以某矿山深部急倾斜厚大矿体的赋存条件为背景，从改变采场几何形态和结构参数角度出发，提出将阶段采场顶部改变为拱形结构，开展拱形结构阶段空场嗣后充填采矿法围岩稳定性研究。从采场拱形形态及阶段采场跨高比入手，分析2个因素对采场稳定性影响。研究结果表明：采场拱形形态的设置和跨高比的优化可以提升采场整体稳定性。通过建立阶段采场拱形结构力学承载模型，进行采场拱形形态及跨高比因素的影响权重分析。跨高比对采场综合稳定性的影响最大，影响权重为66.41 %，采场拱形形态对采场的边墙稳定性影响显著，影响权重为94.83  %。综合围岩位移、裂纹演化规律及围岩开裂区等效深度等指标计算结果，确定最优采场结构参数为：采场高50 m、跨度20 m、采场形态特征角55°。

关键词：急倾斜厚大矿体；阶段空场嗣后充填采矿法；采场结构参数；数值模拟；稳定性

中图分类号：TD853.34文献标志码：A开放科学（资源服务）标识码（OSID）：

文章编号：1001-1277（2023）07-0075-08doi：10.11792/hj20230712

引 言

急傾斜厚大矿体在中国分布较为广泛，对于此类矿体，国内外矿山大多采用阶段空场嗣后充填采矿法、分段凿岩阶段空场采矿法和无底柱分段崩落采矿法等方法开采。其中，阶段空场嗣后充填采矿法因其具有回采强度大、劳动生产率高、回采作业安全及采矿成本低的优点而被广泛采用。随着厚大矿体开采方法向高阶段、大结构方向发展，带来了地压控制难度大、采场结构复杂、充填体强度需求提高等问题。此外，对于低品位矿体，采用浅孔、中深孔开采时开采成本高，经济效益低，而采用阶段开采时又存在稳定性控制难题，一旦采场失稳将会带来边墙、顶板垮塌等其他不可预知的后果，所以阶段空场嗣后充填采矿法中采场稳定性的控制是当前首要解决的难题。

针对传统阶段空场嗣后充填采矿法开采时采场稳定性控制的难题，国内外学者从采场结构参数优化和采场顶板支护等方面进行了大量研究。针对采场结构参数的研究，一些学者利用经验类比法，结合基础理论，根据简支梁、荷载传递线性、长宽比梁板法、比例跨度法原理等理论，预先计算获取采场临界跨度和顶板安全厚度，并通过数值模拟进行理论验证，为阶段空场嗣后充填采矿法采场跨度设计提供理论参考［1-3］。一部分学者采用现场试验、相似材料试验及数值模拟试验等手段进行采场结构优化研究［4-8］：分别通过在现场对开采矿体进行原位试验，在室内设计一定比例的缩小模型，在数值分析软件中选择合理模拟参数和破坏准则，实现采场结构参数的初步设计；再通过设立诸如顶板位移量、塑性区面积、应力特性等指标来定量评价不同方案，综合评估采场稳定性，确定最佳采场结构参数。此外，部分采场通过单一的采场结构参数优化无法很好地控制采场稳定性时，往往会结合支护的方式提升围岩稳定性。在采场支护方面［9-11］，一些学者通过建立采场力学模型，结合数值模拟及预控顶技术优化顶板支护工艺，实现对围岩稳定性的控制。上述学者对阶段空场嗣后充填采矿法采场稳定性控制的研究主要集中于采场结构参数和预控顶支护方面，忽略了采场几何结构形态与围岩体、支护体承载特性的相互适应性，且目前的预控顶支护手段无法优化边墙围岩稳定性。不同的采场几何形态开挖后会形成不同的应力分布状态［12-13］，合适的采场几何形态能够有效提升采场顶板及边墙的稳定性，因此对于该采矿方法下采场几何形态的研究具有一定的必要性。

本文以山东某矿山为工程背景，针对其急倾斜厚大金属矿体，拟采用阶段空场嗣后充填采矿法进行开采。为提高采场稳定性，从改变采场几何形态出发，设置拱形采场形态，运用数值模拟手段，结合相关围岩稳定性评价指标，开展拱形顶板条件下阶段采场承载机制的研究，并分析不同采场结构参数的影响，确定采场形态因素和采场尺寸因素对采场稳定性影响的权重占比，最终确定合理的采场结构尺寸及形态参数。

1 工程背景

该矿山生产低品位金矿，矿体平均品位1.05 g/t，低品位矿段位于-850 m中段，矿区围岩破碎、裂隙发育，地表不允许陷落。矿体为典型的绢云母化花岗岩，走向长度580 m，平均厚度90 m，平均倾角70°，属于典型的急倾斜厚大矿体。矿岩力学参数如表1所示。

根据该矿体浅埋厚大低品位的赋存特征，选择具有生产效率高、生产能力大、开采成本低等特点的阶段空场嗣后充填采矿法进行开采。阶段空场嗣后充填采矿法如图1所示，为提高采场围岩的稳定性将阶段采场的顶部设计为拱形结构，阶段采场的底部设计为“V”形结构，2个阶段采场构成1个独立的回采单元。回采单元内分为一步骤矿房和二步骤矿柱，回采时先回采一步骤矿房，待中段内一步骤矿房回采完毕后，再回采二步骤矿柱。采场垂直矿体走向方向布置，在垂直矿体走向方向采场间留设隔离矿柱，隔离相邻的2个采场。采场顶板拱形的设计，采场跨高比如何与采场拱形结构相匹配，是该方法采场稳定性控制的关键因素，故而需要对采场几何形态和结构尺寸参数比2个因素进行研究。

2 阶段采场开采数值模拟方案及模型建立

2.1 模拟方案

将采场顶板与采场斜边形成的夹角定义为采场形态特征角（φ），采场跨度（b）与高度（h）之比定义为跨高比（λ），即λ=b/h，研究采场几何形态和结构尺寸参数比2个因素对采场稳定性的影响。采用采场形态特征角来描述采场拱形几何形态，采用跨高比来描述采场结构尺寸参数比。阶段空场嗣后充填采矿法采场结构参数设计主要包括采场高度、采场跨度、采场形态特征角等因素。采场顶板长为a，采场跨度为b，采场边墙高为hb，采场高为h，采场形态特征角为φ，采场顶板距边墙高度为l，采场模型如图2所示。

采场形态特征角制约着采场边墙及顶板的尺寸与形态，采场跨度影响顶板暴露面积，二者是控制采场综合稳定性的主要因素。因此，本文选择通过控制

边墙高度来控制采场形态特征角的改变，获取最佳采场几何形态参数，在此基础上研究与之匹配的跨高比因素，获取最佳采场结构尺寸参数。根据矿体产状及围岩状态等因素，初选采场高度50 m，具体方案设计如表2所示，共24個数值模拟方案。

2.2 数值模型建立

UDEC软件可以清晰地反映围岩开挖后裂纹发育状况，故而本文采用基于UDEC软件的块体离散元法模拟节理岩体，使用Voronoi法划分块体并建立离散单元模型［14-15］。根据方案所设计采场尺寸的3～5倍，最终建立长180 m、高180 m的平面模型，以采场为中心，将长×高为100 m×100 m区域划分为Voronoi离散块体，采场处Voronoi多边形块体的最大边长设置为2.0 m。为确保模拟计算精度，在距采场边界10 m范围内设置加密区，此处Voronoi多边形块体的最大边长设置为0.5 m，其余范围内Voronoi多边形块体的最大边长设置为1.5 m，离散区域以外的其他区域设置为连续体。采场初始模型如图3所示。

通过试算法获取数值模拟计算的接触参数。首先，根据现场节理调查结果及获取的岩石力学参数经过Hoek-Brown准则折减得到岩体力学参数，建立等效岩体数值计算模型确定接触参数的范围；其次，采用试算法进行单轴压缩数值模拟，得到不同接触参数条件下的等效岩体力学参数；最后，与Hoek-Brown准则折减的参数进行比较分析，确定最终的接触参数，如表3所示。对数值计算模型顶面施加垂直均布载荷，模拟上覆岩层重力，左、右两侧施加梯度水平应力，经计算，初始垂直均布应力为22.95 MPa，初始水平应力为38.02 MPa，垂直应力梯度为2.70×10-2 MPa/m，水平应力梯度为4.05×10-2 MPa/m。

2.3 采场围岩稳定性评价指标

本文通过围岩位移、裂纹数量和围岩开裂区等效深度指标，判断采场开采后采空区围岩是否开裂垮塌、具体垮塌位置及其围岩发生破坏的程度。在保证数值模拟计算精度的同时，考虑围岩内不同区域裂纹分布的差异性特征，将围岩区域离散为2.0 m×2.0 m的最小计算单元，用于统计分析围岩内裂纹分布特征。为了判断采场围岩裂纹是否开裂，提出围岩开裂区概念，以最小计算单元内裂纹产生累计长度（l1）和预置裂纹总长度（lz）的比值为参数，即γ=l1/lz×100 %。通过数值试验可知，当γ值超过45 %时，围岩发生明显开裂，故设置围岩开裂区阈值为45 %，如图4所示。通过阈值计算统计结果生成整个围岩区域的围岩开裂区分布云图，根据云图可以获得围岩开裂区的边界。围岩开裂区边界多为不规则边界，边界上的不同位置距采空区边界深度不同，用其任意一点的深度表示围岩整体的开裂深度和开裂区大小是不准确的。为准确合理表达围岩开裂区的大小，提出围岩开裂区等效深度指标，将围岩开裂区面积（Si）与采空区边界长度（D）的比值定义为围岩开裂区等效深度（d），即d=Si/D，如图5所示。

3 阶段采场数值模拟结果

3.1 拱形顶板角度对采场围岩稳定性的影响

3.1.1 拱形顶板形态（不固定边墙高度）

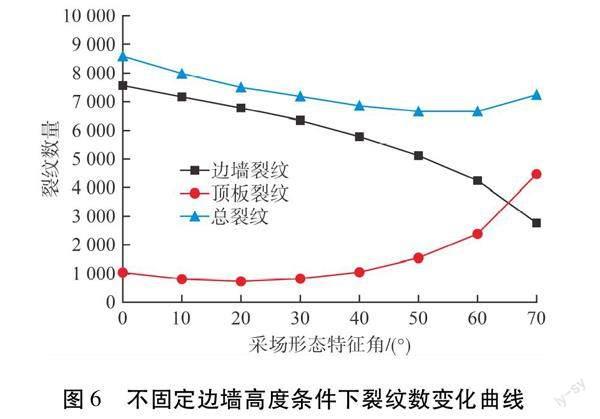
不固定边墙高度条件下，分析阶段采场拱形顶板形态变化对采场围岩内裂纹演化规律的影响，得到了不同形态采场开采后围岩裂纹数量与采场形态特征角之间的关系，如图6所示。由图6可知：对于不固定边墙高度的模拟方案，随着采场形态特征角的增大，边墙裂纹数不断减小，顶板裂纹数量及总裂纹数呈现先减小后增大的趋势。顶板裂纹数最小值在采场形态特征角20°时取得，为732条；边墙裂纹数最小值在采场形态特征角70°时取得，为2 781条；顶板裂纹数最大值在采场形态特征角70°时取得，为4 478条；总裂纹数在采场形态特征角55°时减小趋势逐渐趋于平稳，总裂纹数最小值在采场形态特征角60°时取得，为6 647条。

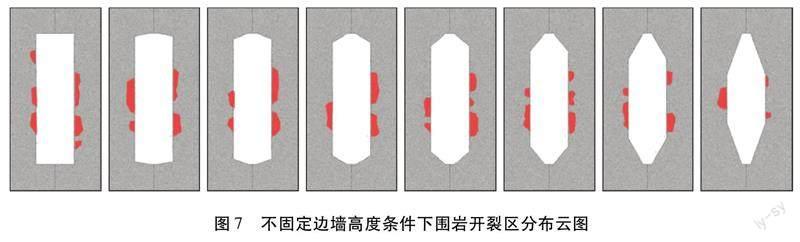
为确定采场开挖后采场边界垮塌破坏的具体位置及破坏深度，对围岩开裂区相关指标进行分析，结果如图7所示。由图7可知：图中红色区域为围岩开裂区，其主要分布在边墙两侧，靠近边墙中心区域，顶板结构处基本没有围岩开裂区分布，故而可以认为跨高比为0.3时，采场开挖后围岩产生破坏的区域主要在边墙处。对围岩开裂区等效深度进行统计，结果如图8所示。由图8可知，不固定边墙高度的方案中，围岩开裂区等效深度随采场形态特征角增大大致呈现下降趋势，其最大等效深度与最小等效深度差值为0.27 m，最大等效深度为0.63 m。

3.1.2 拱形顶板形态（固定边墙高度）

固定边墙高度条件下，分析采场顶板形态改变对围岩稳定性的影响。根据数值计算结果，得到了边墙高度分别为40 m和33 m条件下采场形态特征角与裂纹数量之间的关系，结果如图9所示。

由图9可知：对于固定边墙高度方案，随着采场形态特征角的增大，采场开挖后采空区顶板裂纹数、边墙裂纹数及总裂纹数也随之增大。固定边墙高40 m的方案中总裂纹数最小值在采场形态特征角40°时取得，共6 863条；最大值在采场形态特征角80°时取得，共8 234条。固定边墙高33 m的方案中，总裂纹数最小值在采场形态特征角55°时取得，共6 689条；最大值在采场形态特征角85°时取得，共8 252条。

固定边墙高40 m及固定边墙高33 m方案的围岩开裂区分布云图如图10所示，围岩开裂区主要分布在边墙两侧，顶板区域无围岩开裂区分布。对其围岩开裂区等效深度进行统计，结果如图11所示。由图11可知：固定边墙高40 m方案中，围岩开裂区等效深度随采场形态特征角增大呈现上升趋势，其最大等效深度与最小等效深度差值为0.14 m，最大等效深度为0.74 m；固定边墙高33 m方案中，围岩开裂区等效深度随采场形态特征角增大也呈现增大的趋势，其最大等效深度与最小等效深度差值为0.14 m，最大等效深度为0.57 m。由曲线可以明显看出：固定边墙高40 m所有方案的边墙围岩开裂区等效深度均高于固定边墙高33 m方案，且在边墙高度固定的条件下，采场形态特征角越小，其围岩开裂区等效深度越小，意味着边墙处的围岩愈加稳定。

3.2 跨高比对采场围岩稳定性的影响

采场跨高比的改变将引起围岩位移量的变化，根据数值计算结果，建立采场跨高比与围岩位移量之间的关系，如图12所示。由图12可知：顶板处1号監测点最大下沉位移随跨度的增大逐渐增大，在跨度45 m时最大下沉位移为35.2 mm；跨度小于20 m时，顶板最大下沉位移小于10.0 mm。边墙处2号监测点最大位移随跨度的增大基本没有明显变化，其围岩最大位移维持在100.0 mm左右。从边墙及采场围岩位移数值上来看，采场边墙最大位移数值远大于顶板围岩最大位移数值，由此可见采场围岩位移问题主要发生在边墙处；当跨度增大时，顶板产生的位移逐渐增大，顶板位移过大会产生顶板稳定性问题。

分析不同跨高比采场围岩裂纹数量的演化规律，根据数值计算结果，建立采场跨高比与围岩裂纹数量之间的关系，结果如图13所示。由图13可知：对于跨高比方案，随着采场跨度增大，边墙裂纹数基本不变，在4 600条上下波动，顶板裂纹数在跨高比超过0.4后大幅增大，总裂纹数整体呈现出增大的趋势。总裂纹数最小值在跨高比0.3处取得，共6 631条；最大值在跨高比0.9处取得，共10 581条。裂纹发育的地区主要为边墙区域，两侧边墙裂纹数总和远高于顶底板裂纹数总和，采场跨度增大对边墙裂纹发育无明显影响。对于跨度影响因素，在跨度大于20 m时对采场顶板裂纹发育影响较大。

分析不同跨高比采场围岩开裂区范围的演化规律，根据数值计算结果，建立采场跨高比与围岩开裂区尺寸之间的关系，结果如图14所示。由图14可知：对于跨高比方案，在跨高比较小时围岩开裂区主要分布在边墙两侧，靠近边墙中心区域；随着采场跨度的增大，原采场开挖后产生的围岩开裂区逐步由采场边墙两侧蔓延至采场顶、底部结构处，跨高比0.4为其临界点。且在采场跨度过大时，其顶板产生的围岩开裂区面积将会超过边墙区域，故而高边墙采场的跨度不能设计过大。

计算不同跨高比方案对应的围岩开裂区的等效深度，如图15所示。由图15可知：顶板围岩开裂区等效深度自跨高比0.4起，呈现上升趋势，等效深度最大值为1.02 m，在跨高比0.9时取得。边墙围岩开裂区等效深度于1.10 m上下波动，等效深度最大值为1.25 m，最小值为0.86 m，相差0.39 m。由此可见，边墙长度及采场形态特征角不变时，边墙围岩开裂区面积及等效深度基本不受采场形态特征角及采场跨度影响，采场跨度的增大主要会对顶板围岩开裂区造成较大影响。从等效深度的曲线来看，跨高比控制在0.4时既能保证采场边墙和顶板产生较少的围岩开裂，又能最大限度地开挖。

4 结果讨论

阶段空场嗣后充填采矿法开采时边墙围岩不稳定，跨度较大时顶板会坍塌，为维护顶板稳定性，在一定程度上减小边墙失稳的可能，通过构建一个拱形顶板结构来控制采场稳定性。通过上述模拟结果可知，拱形的顶板结构可以在一定程度上控制采场稳定性。

为分析优化后采场受力状态，对地下采场模型进行简化。假设采场承受垂直均布载荷为q，两侧承受水平均布载荷为kq（k为侧压力系数），在此条件下，将矩形采场顶板简化为一组简支梁，优化后的拱形采场顶板简化为无铰拱，简化建立采场力学模型如图16所示。优化后的采场顶部结构可近似看为拱部结构A′OC′，采场拱形形态的高度、拱面长度等形态特征受到采场形态特征角的制约，拱的跨径主要受采场跨度的制约。拱形结构的受力特点是在拱面受到垂直方向载荷q的条件下，拱脚支撑处产生垂直方向的作用力及水平方向的推力，通过对采场形态特征角的调节，可以间接控制水平推力与垂直作用力的大小。由图16弯矩的分布可知：对于直线顶板AC而言，其主要承受拉应力；对于拱形顶板A′OC′，由于水平推力的存在，使其弯矩M′远小于同跨径下直线型顶板AC的弯矩M，并使整个拱面大部分区域主要承受压应力。岩石具有较好的抗压能力与较弱的抗拉能力，通过拱形顶板的优化，使得原先承受拉力的顶板转变为承受压力的结构，大幅提升了顶板稳定性。此外，因拱形顶板的设计削减了边墙高度，减小边墙承受水平载荷的区域，使得边墙稳定性得以提升。

通过上述力学模型分析，可以得知拱形采场结构形态可以提升采场顶板、边墙及采场整体围岩稳定性。为获取采场几何形态及结构对采场稳定性的影响，对采场形态特征角及跨高比进行权重分析。最小二乘法通过最小误差的平方和进行曲线拟合，可以简便高效地寻找数据的最佳函数匹配，选择不固定边墙高度方案与跨高比方案的裂纹数，进行最小二乘法回归分析，建立采场形态特征角（φ）及跨高比（λ）关于裂纹数（z）的回归模型。采场形态特征角和跨高比具有不同的量纲和量纲单位，为方便后续计算，需要使各指标处于同一量级，对同一指标采用归一化的方法进行处理，将其映射在［0，1］范围内。

将归一化的数据导入SPSS软件中，选择回归分析中的权重估算板块分析，最终获得顶板裂纹数（z1）、边墙裂纹数（z2）及总裂纹数（z3）的回归模型：

z1=3 119.9λ+2 427.8φ+238.5（1）

z2=196.6λ+3 605.8φ+7 835.2（2）

z3=3 473.1λ+1 757.1φ+8 138.73（3）

计算得到顶板裂纹数、边墙裂纹数及总裂纹数的回归模型决定系数R2分别为82.6 %、82.4 %及88.4 %，决定系数值越接近1，代表回归模型拟合效果越好。对其回归系数进行分析，可以得知跨高比改变对采场整体、顶板及边墙稳定性影响权重分别为66.41 %、56.24 %、5.17 %，采场形态特征角改变对采场整体、顶板及边墙稳定性影响权重为33.59 %、43.76 %、94.83 %。数据表明，对于整个采场而言，跨高比改变对采场稳定性的影响起主导作用；对于采场顶板稳定性的影响，同样也由跨高比起主要决定作用；但在采场边墙稳定性的影响上，可以看出跨高比的改变对边墙产生影响极小，基本完全受采场形态特征角改变的影响。

本文提出的拱形顶板阶段空场嗣后充填采矿法，其采场结构参数主要有采场尺寸参数和几何结构形态参数。采场结构尺寸参数中的跨度主要影响采场顶板围岩稳定性，高度主要影响采场边墙围岩稳定性，在采场高度固定的条件下，其采场边墙围岩稳定性主要受采场几何结构形态控制。通过上述分析，可确定采场形态特征角为50°～60°，后续跨高比方案设计时采场形态特征角取55°，结合开采经济条件最终确定最优采场跨度为20 m。

5 结 论

1）针对山东省某金矿急倾斜厚大矿体开采条件，在确保安全高效开采的基础下，改变采场结构，通过引入拱形顶板结构来提高采场稳定性，并在此基础上建立一个基于拱形结构采场的阶段空场嗣后充填采矿法。

2）为预测采场主要破坏区域范围及破坏程度提出围岩开裂区等效深度指标，并建立拱形采场力学承载模型。通过控制采场形态特征角及跨高比来控制采场拱形形态，调节拱脚合力及水平推力大小，减小采场所受弯矩，提高采场抗压性能。

3）获得了跨高比及采场形态特征角对采场稳定性的影响权重，跨高比改变对采场整体、顶板及边墙稳定性影响权重分别为66.41 %、56.24 %、5.17 %，采场形态特征角改变对采场整体、顶板及边墙稳定性影响权重分别为33.59 %、43.76 %、94.83 %。采场综合稳定性主要受采场跨度影响，采场形态特征角主要影响采场边墙稳定性。

4）综合围岩位移、裂纹演化、围岩开裂区及其等效深度规律，确定最优采场尺寸和采场结构形态参数为采场高50 m、采场跨度20 m、采场形态特征角55°。

［参 考 文 献］

［1］戴超群，吴爱祥，鲍伟伟.某急倾斜中厚矿体的分段凿岩阶段矿房法［J］.金属矿山，2018（8）：29-32.

［2］郝益民，宋卫东，张凯，等.阶段空场嗣后充填采场结构参数优化研究［J］.矿业研究与开发，2020，40（3）：15-19.

［3］王志修，曹辉，于世波，等.陡倾双塌陷坑下高阶段采场结构参数优化［J］.中国矿业，2018，27（增刊1）：239-244.

［4］YANG Z Q，ZHAI S H，GAO Q，et al.Stability analysis of large-scale stope using stage subsequent filling mining method in Sijiaying iron mine［J］.Journal of Rock Mechanics & Geotechnical Engineering，2015（7）：87-94.

［5］ZHAO K，WANG Q，GU S，et al.Mining scheme optimization and stope structural mechanic Characteristics for a deep and large ore body［J］.JOM：the journal of the Minerals，Metals & Materials Society，2019，71（2）：1-11.

［6］張瑞明，魏丁一，杜翠凤，等.阶段空场嗣后充填采矿法采场跨度及回采顺序优化研究［J］.矿业研究与开发，2022，42（3）：10-14.

［7］SUN M Z，REN F Y，DING H X.Optimization of stope structure parameters based on the mined orebody at the meishan iron mine［J］.Advances in Civil Engineering，2021，14（8）：1-14.

［8］张建肇，秦忠虎，尚振华.高阶段大直径深孔采场稳定性数值模拟研究［J］.矿业研究与开发，2017，37（9）：86-89.

［9］翟会超，任凤玉，丁航行，等.大结构连跨凿岩硐室稳定性分析及支护模拟研究［J］.金属矿山，2017（4）：12-15.

［10］刘晓辉，曾宪涛，谭伟.预控顶分段嗣后充填采矿法的优化及应用实践［J］.中国矿业，2019，28（3）：87-92.

［11］李启月，刘恺，李夕兵.基于协同回采的深部厚大矿体分段充填采矿法［J］.工程科学学报，2016，38（11）：1 515-1 521.

［12］HEIDARZADEH S，SAEIDI A，ROULEAU A.Evaluation of the effect of geometrical parameters on stope probability of failure in the open stoping method using numerical modeling［J］.International Journal of Mining Science and Technology，2019，29（3）：399-408.

［13］任玉东，周乐，邢军，等.鸡笼山金矿过采区高应力下采场稳定性分析研究［J］.中国矿业，2019，28（7）：119-123，129.

［14］王桂林，王润秋，孙帆.块体离散元颗粒模型细观参数标定方法及花岗岩细观演化模拟［J］.长江科学院院报，2022，39（1）：86-93.

［15］HE S D，LI Y R，AYDINA.A comparative study of UDEC simulations of an unsupported rock tunnel［J］.Tunnelling and Underground Space Technology，2018，72（2）：242-249.

Stope structure optimization and stability control of stage open stoping and subsequent filling mining method for deep low-grade resources

Sun Xing1，An Long2

（1.Xihe County Zhongbao Mining Co.，Ltd.，Shandong Gold Group; 2.Key Laboratory of Ministry of Education on Safe Mining of Deep Metal Mines，Northeastern University）

Abstract：In response to the challenge of controlling the stability of the surrounding rock of stope with stage open stoping and subsequent filling mining method，taking the occurrence conditions of the deep steep-inclined thick ore body in a mine as the background，and from the perspective of changing the geometric shape and structural parameters of stope，it is proposed to change the top of stage stope into an arch structure，and carry out the research on the stability of surrounding rock with arch structure stage open stoping and subsequent filling mining method.Based on the arch shape of the stope and the span-height ratio of the stope in different stages，the influence of the 2 factors on stope stability is analyzed.The research results show that the setting of the arch shape and the optimization of the span-height ratio can improve the overall stability of the stope.By establishing the mechanical bearing model of the stage stope arch structure，the influence weight of arch shape and span-height ratio factors is analyzed.The span-height ratio has the greatest influence on the comprehensive stability of the stope，with an influence weight of 66.41 %，and the arch shape of the stope has a significant influence on the stability of the stope side wall，with an influence weight of 94.83 %.Based on the calculation results of surrounding rock displacement，crack evolution law，and equivalent depth of surrounding rock cracking zone，the optimal stope structure parameters are determined as follows：the height of stope is 50 m，the span is 20 m，and the stope mophorlogy characteristic angle is 55°.

Keywords：steeply-inclined thick ore body;stage open stoping and subsequent filling mining method;stope structural parameters;numerical simulation;stability

收稿日期：2023-04-14； 修回日期：2023-05-15

基金項目：“十四五”国家重点研发计划课题（2022YFC2903802）

作者简介：孙 星（1987—），男，工程师，硕士研究生，从事金属矿床地下开采技术研究与生产管理工作；E-mail：965961946@qq.com