基于改进核联合稀疏表示的高光谱图像分类算法

李佳逊

（南阳师范学院，河南南阳 473000)

0 引言

高光谱遥感图像包含地表物体上大量的光谱信息和空间信息，通过对高光谱遥感图像进行分类，可以实现对地物目标的识别，是实现对地观测的重要手段。目前广泛应用于环境监测、精细化农业、海洋勘探[1-3]等领域。由于训练样本标记数量有限，这会导致数据“维数灾难”[4]，这些问题对高光谱数据分类带来巨大挑战。目前，常用的高光谱遥感图像分类方法包括：K-近邻法(K-Nearest Neighbor,KNN)[5]、支持向量机(Support Vector Machine,SVM)[6]、稀疏表示(Sparse Representation,SR)[7]、深度学习(Deep Learning)[8]等。稀疏表示作为一种新型机器学习分类器受到研究人员的广泛关注，该方法需要对原始图像进行降维，利用光谱特征进行样本分类，没有考虑图像的空间特征。同时高光谱遥感图像中往往存在“同类异谱”和“同谱异类”现象，以及其数据结构呈现高度非线性，因此仅采用稀疏表示进行图像分类的效果大多不太理想。

针对上述问题，研究人员将空间信息与稀疏表示相结合，提出了一系列空间信息与光谱信息相结合的分类算法。Chen 等人[9]提出联合稀疏表示(Joint Sparse Representation,JSR) 算法，通过建立测试像元与训练样本集之间的稀疏线性近似，结合残差确定测试像元类别。但是对于非线性可分的数据集，稀疏表示无法进行分类，文献[10]在JSR 基础上提出了一种基于核联合稀疏表示的高光谱图像分类算法(Kernel Simultaneous Orthogonal Matching Pursuit,KSOMP)，核技术可将那些非可分的数据集映射到一个线性可分的特征空间，从而提高分类精度。Zhang 等人[11]利用核技巧和加权方法，提出非局部加权核联合稀疏表示方法，有效利用邻域像元的相似性，分类精度有了明显提高。受正则化启发，文献[12]提出近邻正则化核联合稀疏表示(Nearest Regularized Kernel Joint Sparse Representation,NRKJSR) 分类算法，自适应优化邻域权重，进而优化加权相邻像素的重构误差的总和。

考虑邻域外的像元也存在光谱信息相近的情况，以及噪声及区域边界对分类效果的影响。我们对原始数据进行滤波处理、降维和超像素分割，来保护边缘像元和充分提取图像空间信息；将邻域像元和超像素分割得到的像元相结合，通过谱聚类算法对参与核联合稀疏表示的像元进行筛选，选出优质像元作为测试样本集；在确定类别时，将核联合稀疏表示的残差与基于超像素分割的KNN算法相结合，在决策函数中加入正则化参数，用残差和KNN算法得到的距离共同确定测试像元的类别。

1 基本原理

1.1 递归滤波处理

递归滤波[13]可以去除图像中的纹理和噪声，同时很好地保留了图像的尖锐边缘和边界。具体地说，给定一个变换域Un，将原域U中的一维信号I转换到新域Un中，则一个输入信号I可以转换为一个域转换信号，如下所示:

其中，Ii为第i个输入信号。Un表示第n域变换信号，δs和δr分别为滤波器的空间参数和距离参数。经过域变换处理后，对变换后的信号进行射频处理如下:

其中，Jn是第n个信号的滤波输出结果，a=为反馈系数，且a∈[0,1]，通过调节a实现图像的平滑。

定义变换域中相邻信号Un与Un-1之间的距离为（|新域Un中的相邻样本之间的欧几里得距离必须等于原域U相邻样本之间的欧几里得距离）。随着c增加，ac→0，公式(1)的递归过程会逐渐收敛，迭代终止，在变换域Un中，位于同侧信号的两个样本距离会越来越近，而位于不同侧的两个样本则距离越来越远，从而起到了对边缘信号的保护作用。

1.2 熵率超像素分割

超像素分割[14]是一种将图像按照纹理、颜色和其他具有视觉意义的特征进行分块的图像分割技术，该方法广泛应用于图像处理和机器视觉领域，可以充分利用高光谱图像的空间信息。

文中采用的是改进的超像素分割方法——基于图上随机熵率的超像素分割方法[15]。具体的目标函数表达式为：

式(3) 分为两部分，H(A)是熵率项，B(A)是平衡项，参数λ≥0是控制熵率项和平衡项贡献的权重。

如果说熵率项是为了获得紧凑和均匀的集群，那么，平衡项就是有利于降低不平衡的集群个数，使集群能够具有相同的尺寸，定义：

NA代表对图进行分割之后获得子群的数目，ZA为集群成员的分布，pZA(i)为第i个子集项中所含点数比例大小。

针对高光谱遥感图像而言，主要使用超像素分割对图像进行空间特征的提取。首先需要通过特征变换的方法，将原始数据转换到低秩特征空间，常用的方法是采用主成分分析得到图像的前三个主成分光谱波段，然后使用图像的光谱信息和空间信息进行熵率超像素分割，采用贪婪算法有效地得到分割后的图像块，从而得到图像中每个像元的分割标签。

1.3 核稀疏表示模型

高光谱图像的高维特性、不确定性、信息冗余以及噪声等原因，导致高光谱数据结构极其复杂，利用传统的线性分类算法得到的分类结果有待于进一步提高。核函数可以将高维数据集映射到特征空间中，在这个特征空间中，数据集为线性可分的[10]。原始向量空间的核函数可定义为特征空间中元素内积的形式：

文中采用的是径向基核函数：κ(xi,xj)=exp(-γ。

给定一个原始像元x∈ℝB，φ(x)为该像元在特征空间中的表示形式，原始空间中像元x的核稀疏表示为：

Aφ的列向量表示训练样本在特征空间中的表示形式，α′为像元x的稀疏表示。原始空间中的核线性稀疏模型为：

K0为稀疏度，上述问题可以通过基于核的正交匹配追踪算法求解。

(Aφ):,m为第m类训练样本，为像元x在特征空间中用第m类训练样本表示的稀疏系数矩阵，(kA,x)m表示特征空间中像元x与第m类训练样本的核表示，(KA)m,m表示特征空间中训练样本集A中第m类训练样本的核表示。

1.4 核联合稀疏表示模型

高光谱图像除了光谱信息外，还存在丰富的空间信息，例如邻域像元属于同一类的可能性很大，因此提出核联合稀疏表示模型，利用了邻域像元的空间相关性，默认邻域像元具有共同的稀疏模式，即邻域像元的稀疏矩阵中非0元素在同一行。

原始邻域像元集X=[x1,…,xT]在特征空间中的表示形式为：

行稀疏矩阵E′的求解可表示为如下的优化模型：

计算每类训练样本对应的重构残差：

测试样本x的最终类别为具有最小重构残差的类别：class(x)=。

2 基于改进核联合稀疏表示和KNN 算法的高光谱图像分类算法

2.1 基于超像素分割的KNN算法

虽然超像素分割方法的原理是将光谱信息相似的像元定义为相同的超像素，但是超像素块包含的像元越多，同一超像素中属于同一类别的概率就越低，如果超像素块中所有的像元都参与测试样本的分类，将会存在一定的误差，另一方面，在选择训练样本时也存在随机性和同类异谱、同谱异类的现象。因此，对超像素像元集XC进行KNN 算法，通过k1参数的设定，筛选出每类中最具有代表性的训练样本，通过k2参数的设定，筛选出超像素块中最具有代表性的测试样本。算法步骤如下：

图1 基于改进核联合稀疏表示算法流程图

设第c个超像素块XC中有n1个像元，XC,{i}为XC的第i个像元，Am为第m类训练样本，包含n2个训练样本，Am,{j}为第m类训练样本的第j个像元，定义XC,{i}与Am,{j}的距离：

Step1：依次选择n2个训练样本，计算d(XC,{i},Am,{1}),…,d(XC,{i},Am,{n2})；

Step2：按从大到小的顺序依次排列，重新定义为d1(i,1),…,d1(i,k1),…,d1(i,n2)；

Step3：选择与前k1个训练样本的距离的平均值作为第i个测试像元XC,{i}与第j类训练样本Am的距离，定义为：；

Step4：依次计算n1个测试样本与第m类训练样本的距离d(XC,{1},Am),…,d(XC,{n1},Am)；

Step5：按从大到小的顺序依次排列，重新定义为d(1,m),…,d(k2,m),…,d(n1,m)；

Step6：选择前k2个数的平均值作为第C个超像素块XC与第m 类训练样本Am的距离，定义为：；

Step7：每一个像元x与各类训练样本集的距离：d(x,Am)=d(XC,Am),x∈XC.

2.2 超像素分割和邻域相结合的核联合稀疏表示模型

在实际情况中，邻域以外的像元也存在光谱信息相近的情况，只考虑邻域像元，会造成空间信息利用不充分的情况，会直接影响分类结果。而超像素分割后的图形区域恰好弥补了邻域的缺陷，同时，在这些选中的区域内，同谱异类和同类异谱的现象普遍存在又无法避免，因此提出超像素分割和邻域相结合的核联合稀疏表示模型，对参与核联合稀疏表示的像元进行筛选，选出优质像元集。具体步骤如下：

定义与测试样本x属于同一超像素的像元集定义为XC，邻域内的像元集定义为XL,定义混合像元集XM={XC,XL}；

Step1：计算XM的相似度矩阵，定义为W；

Step2：若W中的所有元素均大于参数δ，令X=XM进行步骤(4)，否则，Step3；

Step3：利用谱聚类将XM分为两类，定义x∈X(1)，其余为X(2)，若X(1)所包含的像元个数超出X(2)所含像元个数或与X(2)所含像元个数相差不大，则X=X(1)；反之，X=X(2)；

Step4：利用公式计算相关矩阵

Step6：更新迭代次数t=t+1；

Step7：索引集Λ=Λt-1，稀疏系数矩阵=((KA)Λ,Λ+λI)-1(KA,X)Λ,:；

在确定测试像元的类别时要同时，考虑超像素像元和邻域像元，在决策函数中加入正则化参数ξ，来平衡两者之间的关系，如式(13)所示：

3 实验结果及分析

3.1 实验数据集

为了验证本文方法的有效性，使用两个广泛使用的真实数据集Indian Pines和Salinas高光谱数据进行实验。

Indian Pines数据集：由机载成像光谱仪采集的位于印第安纳州西北部关于印第安纳松树的高光谱影像，空间分辨率为20 m，波长范围为0.4～2.5 微米，由145×145 个像素点和220 个波段组成，除去吸水和噪声波段后保留200个有效波段，数据集中的地物类别共16 类，有几类地物如Alfalfa、Grass-pasture-mowed和Oats等的样本数量非常少，这在一定程度上为分类增加了难度。

Salinas数据集：由机载成像光谱仪采集的位于美国加利福尼亚州的Salinas山谷所成的影像，空间分辨率3.7m，波长范围0.4～2.5 微米，由512×217 像素点和224 个波段组成，除去吸水和噪声波段还保留204 个有效波段，数据集中的地物类别共有16类。

3.2 实验结果

Indian pines 实验中随机抽取各类样本的10%作为训练样本、剩余90%作为测试样本，邻域大小为9x9，k1=5，k2=9，稀疏度k0=25，超像素块N=2 800,正则化参数λ=0.2，取10 次实验的平均值作为最终的实验结果。Salinas实验中随机抽取各类样本的5%作为训练样本、剩余95%作为测试样本，邻域大小为7×7，k1=5,k2=9,稀疏度k0=20，超像素块N=3 500,正则化参数λ=0.3，取10次实验的平均值作为最终的实验结果。分别与OMP、KNN、SVM、SOMP、KSPCK 方法进行对比，评价标准有总体分类精度(OA)、平均分类精度(AA)、Kappa系数三个指标。

Indian pines实验中，OMP、KNN、SVM方法的分类精度均不超过85%，并且含有很多离散错分点，如图2(a-c)所示；SOMP、KSPCK 方法的分类精度分别为95.88%和98.40%，而本文方法的分类精度为99.06%，边界更加清晰，小样本地物的分错率更低。除此以外，由表1 得，第1、6-9、13、15 类地物的分类精度为100%。

表1 Indian pines及Salinas数据集分类精度对比

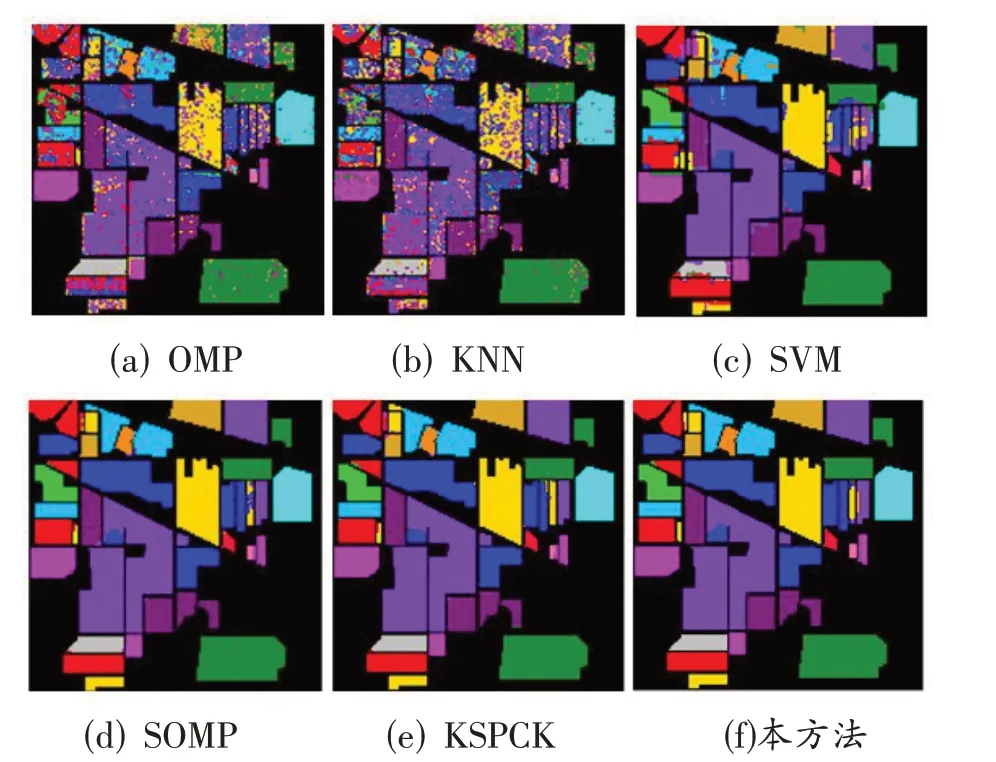
图2 Indian pines数据集分类图

Salinas实验中，OMP、KNN、SVM方法的分类精度均不超过86%，并且含有很多离散错分点，如图3(a-c)所示；SOMP、KSPCK 方法的分类精度分别为92.55%和96.54%，而本文方法的分类精度为98.78%，边界更加清晰，小样本地物的分错率更低。除此以外，由表1得，第1、3、9、11类地物的分类精度为100%。

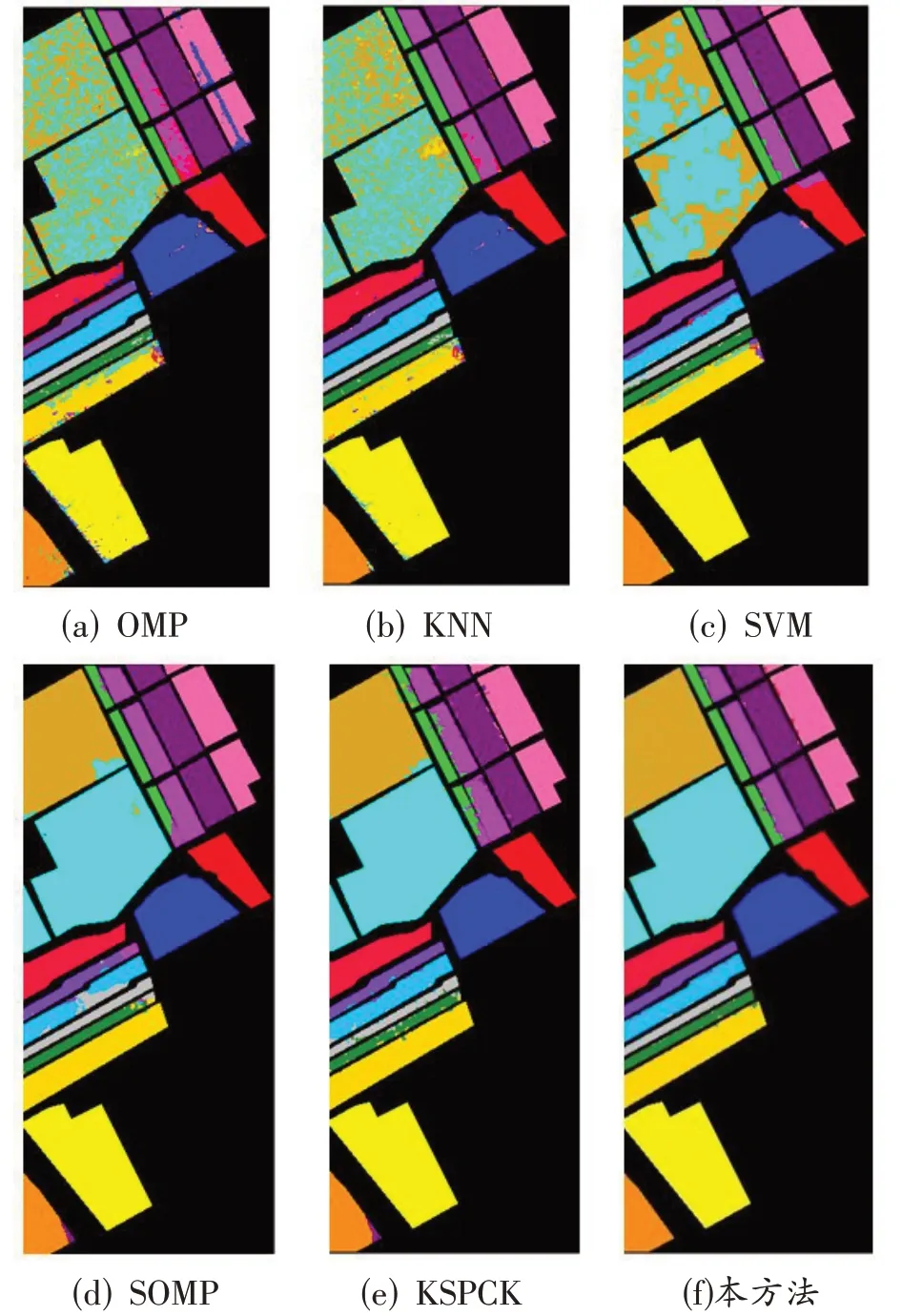
图3 Salinas数据集分类图

4 结论

针对高光谱图像同谱异类和同类异谱现象以及边界噪声对分类精度的影响，提出一种基于改进核联合稀疏表示和KNN 算法的高光谱图像分类方法。利用光谱信息和空间信息，将邻域像元集和超像素分割像元集相结合，通过改进的核稀疏表示计算残差，再通过KNN算法计算测试像元与各训练样本集的距离，最后建立决策函数完成分类。与其他方法相比，整体分类精度与每类分类精度都有明显提高。