基于时空相关性的交通物联网缺失数据填补算法

梁庆，付青坤，田海安，彭志浩

(1.中铁城市发展投资集团有限公司，四川成都 610000；2.长安大学信息工程学院，陕西西安 710064)

0 引言

随着以交通物联网为基础的智慧高速的发展，通过全面感知道路基础设施、行驶车辆等交通参与方的数据，可有效开展面向安全和效率的主动智慧管控，为基于车路协同的无人驾驶提供技术支撑，提升交通运输的安全性、高效性和舒适性。

然而在智能感知的过程中，一方面，由于智能网联汽车的数量快速增长，带来的海量数据传输和计算问题更加突出；另一方面，移动边缘计算的介入，车载移动端和路侧设备之间数据的无线传输占比增加，而由于车辆的移动性和传输环境的时变性，导致多径传输和多普勒效应也愈加突出。上述问题会使数据采集时存在缺失和误码的概率提高，然而由于部分业务具有严苛的实时性要求，不能采用出错重传机制，因此，在接收端对关键数据进行自主的前向纠错，重建缺失数据将是必然选择。

数据缺失主要来自两方面：一方面，传感器的故障会导致不定期的数据空白，这种缺失往往持续时间较长，很难用算法进行填补重建，不属于本文研究的范畴。另一方面，由于数据传输过程中的信道噪声，而导致的零星误码或缺失，可通过本文的方法进行数据填补重建，这是本文的研究内容。

当前，数据重建技术分为时域、频域和空域三大类。对于时域重建技术，主要依据同一传感数据在时间序列上的相关性进行数据填补，文献[1]从已有数据中提取不同类型的数据基信号，并利用基于时间序列的线性关联映射重建缺失数据。文献[2]基于传感数据在一个嵌套滑动窗口内的相关性，提出一种数据流缺失恢复方法。文献[3]提出一种针对缺失数据的谱分析方法，通过更新估算因子来修正时域重建算法，提高数据重建精度。

文献[1-3]均利用了时域数据的随机平稳特性，适合数据变化不大的静态物联网领域。例如河道水位检测、交通基础设施的状态检测等。但对于车速、断面流量等和交通流密切相关的实时交通元素，数据虽然具有广义随机平稳特性，但时域变化剧烈，时域相干窗口较小，在此窗口内采集到的原始有效数据较少，提取的特征值往往离散度大，若加大插值窗口又会导致缓存数据过多，处理时延长，且数据的时域关联性呈时间选择性衰落，适用性难以保障。

关于数据重建在空域中的研究，主要通过分析多个传感器在空间部署位置的相关性来提取传感数据的属性特征，进而估计缺失数据。文献[4]提出一种KNN算法，通过在特征空间中寻找与缺失数据属于同一类的相邻K个样本，对其加权平均后估计并重建缺失数据。文献[5]将逻辑回归模型与多重插补算法相结合，但该方法仅适用于缺失率较低的情况。文献[6]则提出一种基于压缩感知的低秩数据重建算法，利用传感设备存在的空间相关性和数据的低秩特征，重建缺失数据，然而其低秩特征并不适合多类型混合接入的交通物联网采集系统。

随着以机器学习为代表的人工智能算法的兴起，通过强大的计算机算力，在交通大数据中提取非线性的时空属性特征，搭建多粒度的数据格式以及数学描述方法，重建缺失数据，已成为研究热点。文献[7]利用相邻传感节点的小波系数相关性，通过逆小波变换和时频回归模型来重建缺失数据，该方法精度高，但实现复杂度偏高。文献[8]利用逆向传播(Back Propagation，BP)神经网络对单一的交通流量进行预测，但并不适用于具有非结构化特征的交通物联网数据。

在公路交通领域，机电设备的类型适中，空间部署呈线性分布，具有明显的空间相关特性，且感知对象聚焦于交通流、交通事件、气象等固定类型，但数据具有一定“定时漂移”特征，即“此时此处”的数据和“彼时彼处”的数据更具相关性。因此，本文通过分析高速公路交通感知数据的特性，提出一种基于时空相关性的线性插值神经网络(LIN_BP)数据恢复算法，将时域和空域特征相结合来恢复缺失数据。

1 基于时域平稳性的线性插值预处理

目前，在公路交通领域中，在靠近传感器的感知接入层，仍然有较多非智能感知设备，例如输出电流信号的液位计，电压信号的压力传感器，这些设备有些部署无法进行有线传输的移动终端，有些是后装的感知设备，不具备有线传输条件，无奈采用无线传输方式。一旦数据接入路侧设备后，就会采用更加可靠的光纤有线传输。因此，本文重点针对因无线传输导致的数据缺失。

由于无线传输环境的开放性和时变性，数据传输过程中经常会受到各种干扰和噪声的影响，例如车辆马达产生的宽频干扰脉冲和毛刺噪声，这些干扰会导致信号传输出现连续的误码，而常用的卷积码加交织的信道编码技术，仅对零星的非连续误码有效，因此，有必要对数据进行预处理，将连续的缺失数据或异常数据位变为零星的单个孤立缺失数据位。

对于多数输出模拟信号的传感器，在连续时间内采集到的非电量数值非常相近甚至相同。因此，可利用感知数据的时间相关性，构建线性函数来粗略估算缺失数据。该方法优势在于复杂度低，适合对时延敏感的实时性业务。

线性插值的基本原理是：假设ti时刻的数据xi缺失，在其附近的tp和tq时刻的传感器数值为xp和xq，经过线性插值后的估计值为

插值窗口尺寸M的选择至关重要，若取值太小，缺失数据点占比过高，容易受到周围噪声和毛刺的影响，影响插值的精度。若取值太大，计算复杂度升高，导致产生较大的处理时延。一般的经验原则是，在插值窗口内，缺失数据点占比不超10%，且与待重建信号的中心频率成反比，频率越高，说明数据变化越快，时域相干窗口应越小。通过选择合适的窗口大小，对多个缺失数据进行预处理后，得到初步数据重建结果。

在上述方法中，只是针对一个传感器在时域的时间相关性，同时由于选择窗口尺寸K时的两难顾虑，实际效果并不理想。因此，还应兼顾传感器在空间位置的相关性，进行时空二维联合处理。

2 基于时空相关性的交通感知数据分析

在交通物联网中，对同一物理量的检测通常采用多点布设传感器的方式，例如在一段公路上多个门架设备对车速，车流量的连续检测。这些传感器在同一时刻对各自负责的区域进行信号采集，由于部署在公路沿线的传感器位置存在空间相关性，数据也会呈现一定的相关性。若某个传感器出现故障或受到强干扰，导致采集数据缺失，可通过相同时间不同点位的其他传感数据来估计缺失值。

但这种相关性由于受到路面质量、交通流、交通信号控制等多方面的影响，交通流特征和环境参数并不是线性变化，很难用简单的线性解析数学模型来刻画，因此，需引入非线性的预测和分析手段。BP神经网络是一种智能算法，通过相当数量的训练找出模式与类别之间的内在联系，以隐性方式学习和存储输入-输出模式之间的非线性映射关系，因此，本文综合利用感知数据在时间和空间的相关性，建立基于BP神经网络的数据重建模型，最后得到缺失数据的估计值。

这里的时空相关性表现为两个方面：

1)时域相关性。同一传感器在相邻时刻（相干时间内）采集到的数据之间存在的时间相关性，超出相干时间，数据之间的关联性明显下降。

2)空域相关性。相邻传感器（相干距离内）在同一时刻采集到的数据之间存在的空间相关性，超出相干距离规定的空间范围，数据之间的关联性明显下降。

图1为高速公路微波检测器的区间车流量的时空检测数据。横坐标表示采样时刻，也就是以该时刻为终点，过去一段时间内统计得到的车流量。纵坐标是检测点位，对应不同的空间位置，不同的几何外形表示不同的ABCDE传感器。观察矩阵图中数据发现，A检测点在时刻1 的数据(93)，与B 点在时刻2 的数据(94)相关度更高。也就是说，沿对角线上的数据关联程度明显高于水平线和垂直线上的关联度。原因在于，不同传感器的部署位置不同，检测数据具有一定“定时漂移”特征，即“此时此处”的数据和“彼时彼处”的数据更相关，类似“绿波带”的交通流“流动”特性。

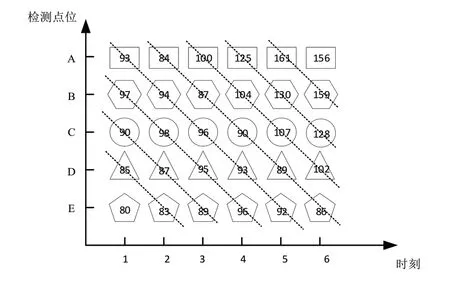
图1 时空二维车流量数据矩阵

图2是同一路段内相邻5个检测点的车流量变化曲线，图中每一条折线对应一个检测点。这也是从另一个角度描述数据的时空关联性。对比图1 和图2，图1中对角线的斜率，图2中两条折线的平移间隔，都反映了该路段的平均车速。

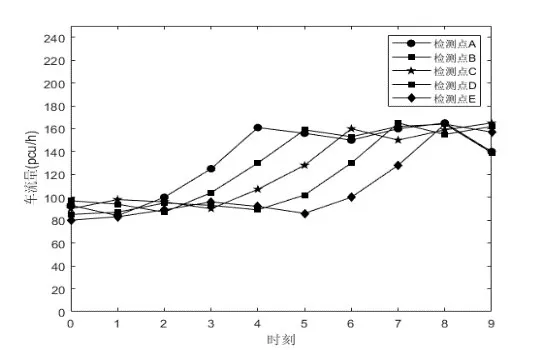
图2 相邻检测点车流量变化曲线

图3 是检测点车流量随时域统计窗口变化的曲线。可以看出，若统计窗口较小，此时段内通过的车流量不稳定，随机性更强，两个检测点检测到的车流量数据相差较大，但随着窗口的增大，数据趋于稳定，两个检测点的车流量数据差距越来越小，逐渐趋于相等。例如，在一天的统计窗口内，若两个检测点之间没有进出闸道，那么观察到的车流量几乎相同，此时的时域关联性对填补数据没有帮助。

需要注意的是，数据的相关性不仅与车流量统计窗口大小有关，还与传感器的布设间隔有关。图4是在采样时间间隔固定的条件下，不同的检测点采集的车流量随采样距离变化的曲线。

图4 基于距离的车流量变化曲线图

从图4可以看出，传感器布设间隔越大，车流量的相关性越小，当两个传感器的距离在2km 以上时，A点和B 点的车流量并没有明显的正相关。这是因为交通流量自身的弥散效应，随着检测点距离的增加，两处检测数据的关联程度会更低。

3 基于时空相关性的数据填补算法

由于数据之间不仅存在时间上的相关性，在空间上也存在一定的相关性，若使用单一的时域线性插值，对缺失多个数据或缺失较长时间的情况下填充效果不理想，且影响时空关联的因素涵盖传感器间隔、车辆速度、采样频率等，很难用线性模型表示，为此，本文引入非线性的BP 神经网络，其网络结构如图5所示。BP神经网络包括输入层、隐含层和输出层[9]。同一层各个神经元无连接，层与层之间神经元全连接，右下角特写部分是单一神经元内部的计算操作。正向传播是从输入层神经元到隐含层再到输出层逐层计算[10]，若输出层未得到期望的输出，则使用梯度下降法沿连接线反向传播误差，逐层更新权重ω和偏差b，直至目标函数的误差满足要求，训练完成。神经网络的传播都是线性矩阵运算,为了解决线性模型所不能解决的问题，需要在隐藏层中加入非线性的激活函数f。

图5 BP神经网络结构图

BP网络的核心是以相邻若干节点（空域）和相邻时刻（时域）的已知数据作为网络输入，以缺失数据的预估结果作为输出，通过一定量的样本学习训练，将诊断知识隐性存储于网络的拓扑结构和连接权值ω和b中，形成从已知数据值到缺失数据预估值之间的非线性映射关系。

在此映射过程中，输入层神经元个数取决于输入数据的时空选择区域，其中，空域对应相邻感知节点的数量，时域对应第2节提到的插值窗口。时空选择区域对算法的性能影响重大，选择区域太小，时空关联窗口小，恢复的数据准确性较低；而选择的区域太大，输入的神经元节点过多，训练时间长，影响数据填补的实时性。

因此本文选取3～8 个。采用计算速度更快的ReLU 激活函数，用Adam 算法优化模型，减小损失函数，当训练选取的样本数batch_size 选择32 且学习率设定为0.001 时模型的误差最小。本场景中，输出层输出是一个估计值，故神经元个数为1。由于传感器沿公路线型布局，结构简单，为了提高算法的收敛速度，本文选取一层隐含层，隐含层神经元个数为输出层的两倍。

假设在某高速公路上，每隔1km有一个微波车辆检测器，实时检测交通流量、平均车速、车型及车道占用率等交通数据，如图6所示，一般意义的数据xi,j中，下标i表示时间，下标j表示空间传感器的编号。图6中，浅灰色背景的数据为输入数据，可采用“十字”“对角线”“环形“三种策略，对应的输入数据点数量分别为4、6、8。深灰色背景的B2为缺失数据。

图6 输入数据选择示意图（输入个数为4，6，8)

推广到一般情况，为了将时空二维数据输入到BP网络中，需经过并串转换后变为一维数据，暂时忽略其时空特性。示意图如图7所示，此处只列出连续5个传感器(A,B,C,D,E)的数据。其中，为i时刻所有检测点的数据的集合向量。并串转换后的一维数据集合为X={x1,x2,x3,…,xK}，其中K=(M+1)N。根据第2节的时空特性分析，输入检测点的数量（图6矩阵的行数）、插值窗口（图6矩阵的列数）和选择策略共同决定输入神经元的个数。

图7 并串转换示意图

在输入图5所示的BP网络时，输入数据集为XK={x1,x2,x3,…,xK}，输出为待估计数值，对应原始数值为yk，理想情况下=yk。为了训练模型，将多个样本数据集分为训练集和测试集，其中训练集为T={XK,yk}。

BP网络的优化流程如下：

1)初始化BP网络。对网络层里的所有权值和偏置进行(0,1)范围内随机初始化，设置最大迭代次数epoch和最小误差值eps；

2)输入训练集T={XK,yk}；其中yk是实际标记的缺失值，XK是以yk为中心，从时空二维拓展获得的一系列已知训练数据；

3)根据图5的BP网络模型正向计算输出值；

5)将误差ek反向传播到隐含层神经元，计算误差对每个神经元的偏导数，据此调整连接权重ω和偏置b；

6)重复步骤2 至6 训练样本数据集，直到误差ek的结果小于最小误差值eps或者训练达到epoch为止。

在上述训练过程中，输入的数据集{x1,x2,x3,…,xK}实际为时空二维数据，其中每一个数据对应第j个检测点在第i个时刻的检测数据xi,j。

在实际场景中，由于环境因素的作用，数据缺失点的个数和位置是随机的。在第1节基于时域相关性的线性插值模型中，只针对同一个传感器，但允许存在连续几个缺失数据，需要动态调整插值窗口的大小。而第2节的基于空间相关性的BP算法，尽管输入数据涵盖不同时刻、不同位置的传感数据，但出于计算复杂度和实时性的考虑，假设只有一个缺失点（输出节点数为1)。因此，在不确定缺失数据个数的情况下进行视情处理，可在算法复杂度和填补准确度间取得平衡，具体流程如图8所示。

图8 算法整体流程图

首先对训练集中的缺失数据个数n进行判断。当只有一个缺失数据时，直接使用BP 网络模型进行预估。当缺失多个数据(n＞1)时，需通过LIN模型进行数据估计并得到n-1 个估计值，将训练恢复所得结果与已知数据输入一起输入到BP网络模型中进行预估，整个算法流程中，只需要一个BP 模型进行数据估计。

表1为陕西省岩湾闸道至宝鸡南闸道路段某日的车流量检测部分数据。其中纵坐标为不同的检测点，横坐标为不同的检测时刻，图中深灰色和浅灰色数据均为缺失数据。第一阶段选择合适的插值窗口得到边缘缺失点的数据（表中浅灰色部分的2个数据）；第二阶段将已知数据和第一阶段得到的数据（标深灰的数据）输入到BP模型中，对最后剩余的深灰色点位进行数据预估。

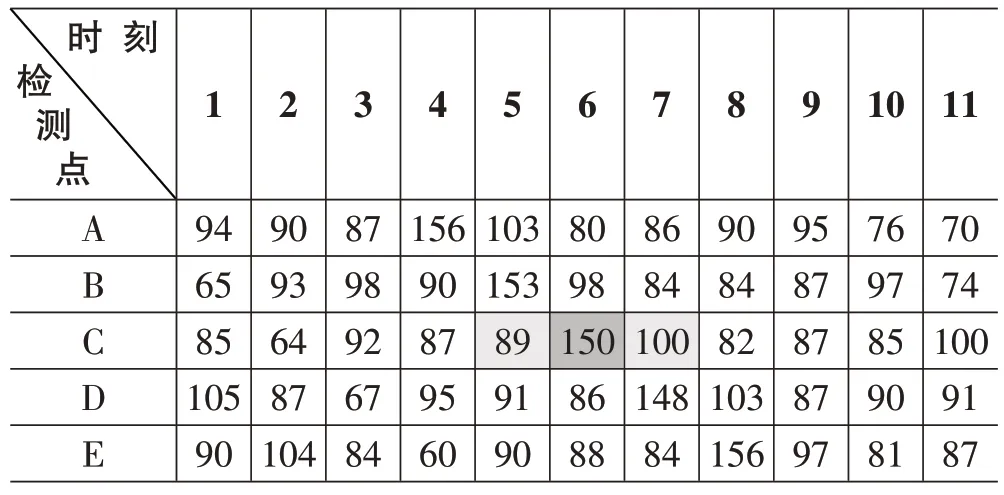
表1 车流量统计表

4 实验与分析

本文使用多个检测点的交通流量真实数据集进行试验。其中数据集的80%作为训练样本，20%作为测试样本。由于该数据集本身的统计窗口较大，实验时选取的感知数据的时间统计窗口取值在5min 到25min之间，在空间维度上，选择以待重建数据的节点为中心，周围3～8 之间的邻居节点。将本文提出的LIN_BP 算法分别与LIN，BP 及KNN 算法[4]进行对比，采用均方误差(Mean Square Error，MSE)衡量算法的填充精度：

其中，yn是真实非缺失数据值为由模型计算得到的估计值。在不同统计窗口下，各算法的均方误差对比结果如图9所示，随着统计窗口的增大，LIN模型和KNN 模型的误差显著增大；而LIN_BP 模型的误差变化并不明显。由于KNN 算法建模的依据仅仅是感知数据的空间相关性，只考虑同一时刻内两个相邻传感器的采样数据，没有考虑车流量的“时移特性”，以及不同统计窗口的影响。而LIN_BP模型同时考虑时域插值窗口和空间相邻节点两种特征的影响，根据缺失数据个数动态调整插值窗口，因此，时域统计窗口对LIN_BP 模型的影响很小，最终预估结果的准确度更高。

图9 时域统计窗口对算法估计误差的影响

从图10 中可以看出，LIN 算法的估计误差最大，KNN 算法的误差随着节点数的增加逐渐变大，BP 算法和本文提出的LIN_BP 算法的误差较小且较为稳定。由于LIN 算法单纯利用时间相关性进行数据重建，面对突发性较强的交通物联网进行数据估计的准确度较低；而KNN 算法仅考虑空间相关性，当相邻节点较少时，估计出的数据值比较准确。但随着邻近节点的增多，数据的空间相关性变得更为复杂，基于该模型进行估计的误差变大；BP算法的误差较小，付出的代价是算法的复杂度高，时延较长。而LIN_BP 模型同时兼顾感知数据的时空相关性，数据重建的效果误差更小，和单纯的BP模型相比，算法复杂度更低。

图10 节点数对算法估计误差的影响

综上所述，本文针对实际场景中的交通数据具有时空二维相关性的特点，提出了一种基于时空相关性的LIN_BP 模型，既考虑同一时刻相邻位置的传感器的空间相关性，也考虑了同一个传感器采集数据的时间相关性，从两方面出发对缺失数据进行预估，在扩大了算法适用范围的同时，提高了数据填补的准确性。

5 结论

本文通过分析交通物联网中传感器数据的特征，提出基于时空相关性的LIN_BP 模型来填充缺失数据。该算法模型同时考虑时间和空间两维度的影响，根据缺失数据个数的不同进行分情况处理，当缺失个数较多时先利用LIN模型进行估计，将结果结合原始数据输入BP模型从而得到最终的预估结果。本文以MSE作为算法性能评价的标准，在真实数据集对本文中提出的模型和几种常用缺失值填补模型进行实验，得出以下结论：相较于基于单一属性的填充算法，本文提出的线性插值与BP神经网络结合的算法能克服由于数据不平稳，统计窗口大而产生的误差，从而使填补精度更高。实验结果表明，本算法的误差小于经典KNN算法。