基于VMD-MD的油气管道泄漏信号去噪方法

路敬祎,李佳丽,侯轶轩,王冬梅,侯 男

(1.东北石油大学 三亚海洋油气研究院,海南三亚 572024;2.东北石油大学 人工智能能源研究院,黑龙江大庆 163318;3.东北石油大学 电气信息工程学院,黑龙江大庆 163318;4.黑龙江省网络化与智能控制重点实验室,黑龙江大庆 163318)

0 引言

近年来,随着我国经济的增长,石油、天然气等的储运量也不断增加,管线运输行业得到了迅速的发展。然而,长期使用后,因腐蚀、焊接、第三方损坏等因素,必然会引起管道运行异常,这样不仅会造成能源、经济、环境等方面的损失,还会威胁到工作人员的生命安全。因此,如何定位油气管道泄漏点[1-4]已成为国内外有关领域的迫切研究内容。我国自20世纪80年代开始,管道泄漏检测技术得到快速发展。目前,管道泄漏检测技术可以划分为三大类:人工巡检法、硬件检测法和软件检测法[5-6]。不仅如此,随着信息传输技术和电子计算机技术的不断发展,管道泄漏检测技术也逐步开始信息化和自动化的改革,将传统的泄漏检测方法与人工智能、物联网等新兴技术融合起来是一大标志。然而,在油气管道泄漏检测过程中,采集的泄漏信号会受到噪声信号的影响,这样不但会引发其误报警、漏报警,而且还会造成监测系统定位不准确的问题。因此,对所采集到的信号进行去噪处理,从而在复杂的环境与条件下,对管道泄漏点进行精确的辨识与定位,始终是该领域的重难点。

HUANG等[7]提出了一种新型的、根据信号自身的尺度特征来进行分解的去噪方式,称为经验模态分解(Empirical Mode Decomposition,EMD),其优点是基函数可以一开始就确定。但是该方法一直存在的问题是端点效应及模态混叠。为了完善上述问题,2014年,DRAGOMIRETSKIY等[8]提出了一种可以自适应地分解信号的方法,即变分模态分解(Variational Mode Decomposition,VMD)。它可以自适应地确定模数,在信号去噪领域具有突出表现,但是其仍然存在不足之处,例如,怎样才能在VMD分解信号后所得到的大量模态分量中区分是否具有纯粹性,并将其重构成一个新信号从而达到去噪目的,仍然是个急需解决的问题。2020年,LU等[9]提出了一种VMD与改进的巴氏距离(Bhattacharyya Distance,BD)相结合的去噪方法,该方法利用改进的BD来衡量两个模态对应的方差之间的相似性,以区分有效分量和非有效分量,并将该方法与EMD进行对比,其具有更好的滤波效果。2021年,王冬梅等[10]提出了一种VMD与板仓-斋藤距离结合的算法,主要是通过板仓-斋藤距离的变化来评估VMD分解得到的大量模态中的有效模态,之后利用小波变换去除筛选后噪声分量的高频噪声,最后将有效分量与滤波后的噪声分量进行重构。2022年,侯轶轩等[11]提出利用海洋捕食者算法(Marine Predators Algorithm,MPA)对VMD算法中的关键参数进行自适应选取,之后计算VMD分解后的各模态分量与原信号的概率密度之间的豪斯多夫距离(Hausdorff Distance,HD)选取有效分量,最后将有效分量进行重构得到去噪信号。可以看出,使用描述各数据间相似性的距离指标来筛选VMD的有效模态是一大热点。

因此,本文提出一种基于VMD与马氏距离(Mahalanobis Distance,MD)相结合的去噪方法(VMD-MD),该方法首先通过VMD算法对信号进行分解,从而获得大量模态分量(IMFs),再依次计算出各分量与原信号间的马氏距离即相似性,从而区分出有效模态分量和无效模态分量,最后对有效模态分量进行重构形成更纯粹的信号。为体现本文所提方法的可行性,将VMD-MD去噪方法应用到仿真信号和实际管道泄漏信号上,并且与其他不同的去噪方法(EMD-HD,VMD-HD,VMD-BD)进行对比。从试验结果上来看,该方法在保证较高的去噪波形还原度的同时,还具有较好的去噪性能。

1 变分模态分解

VMD是一种自适应处理信号的分解方法,可以将原信号分解为拟正交的限制带宽的固有模态函数(Bandwidth-Limited Intrinsic Mode Functions,BLIMFs)[8]。不同于EMD中定义的IMF,这里的BLIMF被视为一个调幅调频(AM-FM)的信号,可以表示为:

BLIMFk(t)=Ak(t)×cos(φk(t))

(1)

式中,k为第k个BLIMF;Ak(t),φk(t)为瞬时振幅、相位。

为了获得目标BLIMF,将VMD中的分解过程转移到一个约束变分模型[8]中,如式(2)所示。具体来说,VMD的分解过程就是利用非迭代筛选结构搜索其最优解。

(2)

式中,uk为各模态函数,uk={u1,u2,...,uk};wk为各中心频率,wk={w1,w2,...,wk}。

为求VMD约束变分模型式(2)的最优解,引入惩罚因子α,并构造出拉格朗日函数:

L({ui},{wi},λ)

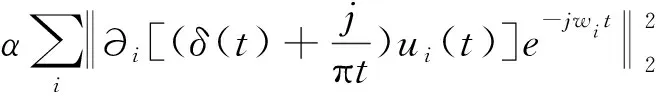
(3)

式中,λ,α为拉格朗日乘子、惩罚因子。

再进行时域转换处理,最后可得到模态分量ui,wi:

(4)

使用交替方向乘子算法求取式(2)的最优解,即原信号被分解为K个模态分量,单个分量的运行步骤如下。

(3)由式(5)更新λn+1。

(5)

(4)当条件满足式(6)时,停止迭代并输出K个模态分量,否则返回步骤(2)。

(6)

2 马氏距离

印度数学家Mahalanobis首先提出马氏距离的概念[12],用来代表不同数据间的协方差距离(其中,协方差是指统计高维度数据或变量间相关性的一个指标)。与欧氏距离(Euclidean Distance,ED)、汉明距离等一样,其是一种可以评估、计算两个未知样本间相似度的性能指标及方法,特点是可以解决高维数据中不同维度之间不独立分布的问题,计算公式[12]如下。

对于一个均值为μ=(μ1,μ2,...,μp)T、均方差矩阵为S的变量X1～Xm,其马氏距离计算公式为:

(7)

计算向量Xi和Xj之间的马氏距离公式为:

(8)

本文中,由于事先未知采集到的信号及VMD分解得到的各模式成分的概率分布,所以必须先计算每个成分的概率密度之后,再计算其马氏距离。

3 马氏距离优选VMD模态

首先,利用VMD对原信号(即输入信号)进行分解,能够得到大量的IMFs;其次,分别求取每个模态与原信号的距离,得到马氏距离分布图后进行比对分析;最后,重构较纯粹信号,得到去噪后信号,即达到去噪效果[5]。

(1)初始化VMD参数,如分解层数、原信号表达式,且经过中心频率法计算确定模数K=7,Sin=S;

(2)根据式(4)对输入信号Sin进行VMD分解,得到模态分量u1,u2...ui;

(3)通过式(6)计算各分量与原信号之间的马氏距离MD1,MD2,...,MDi,用于评估各分量与原信号相似性;

(4)分析数值差异及斜率对比,区分出有效IMF分量与非有效IMF分量;

(5)最后重构有效IMF分量,得到去噪后信号。

4 试验分析

4.1 VMD-MD算法的仿真信号试验

为验证本文所提方法的去噪性能,仿真试验选取含3个频段为2,24,288 Hz的余弦信号,以及高斯白噪声强度为0.05 dB的噪声信号η,作为复合信号,采样点数T=1 000,表达式为:

f(t)=cos(4πt)+0.25cos(48πt)/4

+0.0625cos(576πt)/16+η

(9)

原信号和复合信号的时域波形如图1所示。设置VMD参数,采用中心频率法[13]判断VMD的模数K。该方法主要步骤是计算VMD分解过程中不同K值下得到IMFs的最大中心频率,根据VMD的特征可知,不同的IMFs对应不同中心频率,若有相邻两个IMFs的中心频率相似,即出现模态混叠现象,说明此时K值选取不当。试验结果如表1所示。可以看出,随着K值不断增加,各模态对应的中心频率的间隔逐步细分,直到K=5时,后4个中心频率十分相似,且IMF1和IMF2之间的频率间隔较大,说明此时属于“过分解”状态。

(a)不含高斯白噪声的原信号

(b)复合信号时域波形图1 原信号及复合信号时域波形Fig.1 Time domain waveform of raw signal and composite signal

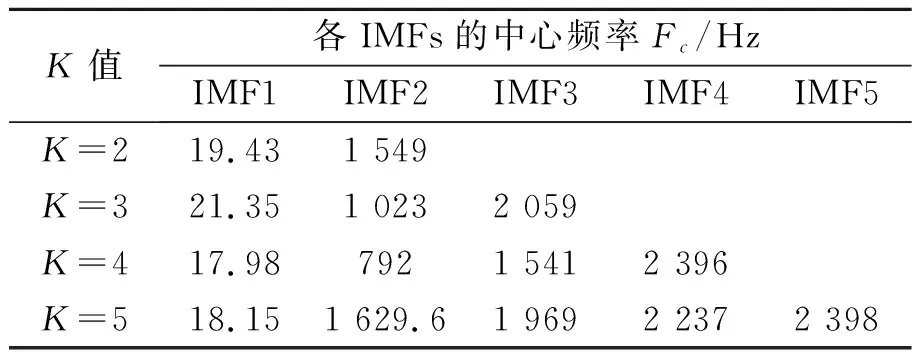
表1 不同K值下的中心频率Tab.1 Center frequency under different K values

因此,初始化VMD参数为惩罚因子α=2 000、模数K=4,以及默认噪音容忍tau=0、总信号拟合误差允许程度tol=10-7,对原信号进行分解,得到4个IMFs波形及相应频谱曲线如图2所示。分别计算各个IMFs的马氏距离,其结果如表2所示。为了更直观地进行观察,绘制马氏距离分布图,如图3所示。可以看出,IMF1和IMF4的马氏距离与其他分量相比具有突变性,因此重构信号由原信号中去掉IMF1和IMF4组成。重构信号波形及去噪前后还原效果对比图如图4所示。可以看出,重构信号几乎复现了原信号,只在波形峰值处存在少量偏差,整体波形趋势一致,有一定的还原性。

图2 VMD所得IMFs波形及其频谱Fig.2 Waveform and spectrum of IMFs obtained from VMD

表2 马氏距离Tab.2 Mahalanobis distance

图3 马氏距离分布Fig.3 Distribution of Mahalanobis distance

(a)VMD-MD重构信号波形

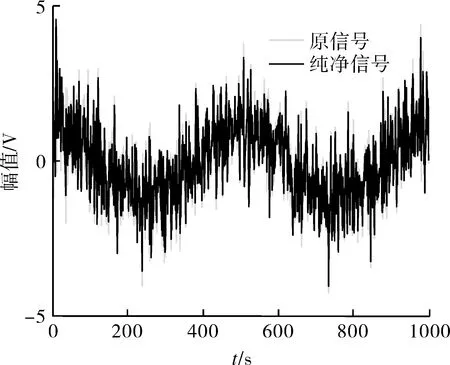
(b)还原效果对比图4 VMD-MD重构信号及还原效果对比Fig.4 VMD-MD reconstruction signal and comparison of restoration effects

为了对比该算法的去噪性能,将其与EMD-HD,VMD-HD,VMD-BD进行对比。图5示出了仿真信号应用不同去噪方法所得重构信号波形图。

(a)仿真信号波形

(b)EMD-HD

(c)VMD-HD

(d)VMD-BD图5 仿真信号不同去噪方法所得重构信号波形Fig.5 Reconstructed signal waveform obtained from different denoising methods for simulated signals

从图5可以看出,EMD-HD方法得到的滤波信号的波形整体振幅较小,边界较为圆滑,存在幅度失真现象;VMD-HD方法的还原效果好于EMD-HD,不过在波形下降区域同样具有幅度过小的问题,导致局部失真;VMD-BD方法的还原效果最差,波形出现了较大程度的失真,整体幅值较小。因此,本文所提VMD-MD去噪方法在对于原信号整体波形幅值的还原程度最高。

4.2 VMD-MD算法的实际信号试验

应用本文结论,在某天然气管线泄漏监测仿真试验平台上,采用HD-Ⅱ管道泄漏探测系统进行了仿真,得到试验数据。实验室管道系统如图6所示,实验室管道整体布局如图7所示。

图6 实验室管道系统Fig.6 Laboratory pipeline system

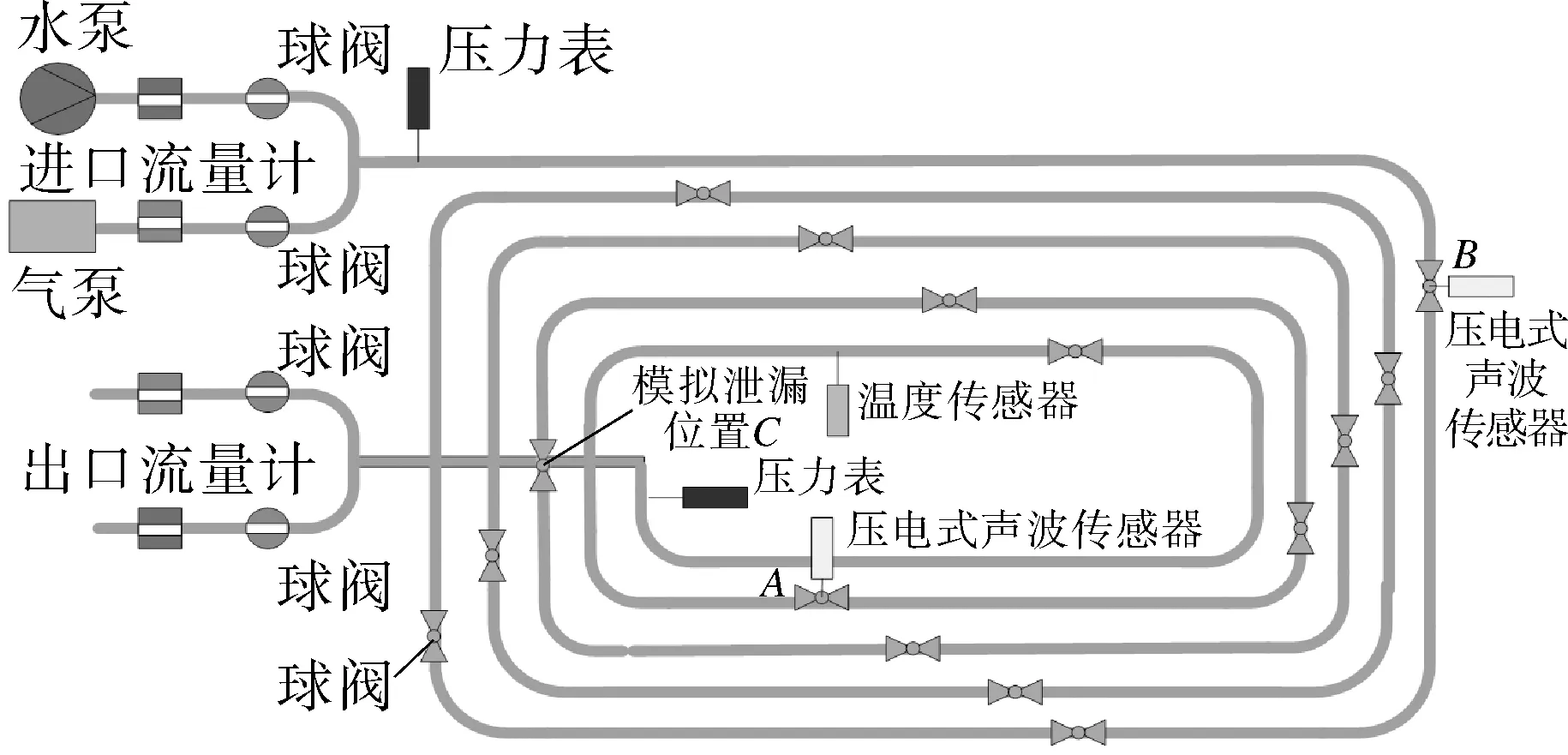
图7 实验室管道整体布局Fig.7 Overall layout of laboratory pipelines

管道每隔10 m安装一个泄漏点,同时用4分球阀连接各个泄漏点,目的是模拟实际天然气管道泄漏现象,共计15个泄漏点;管道流体是由空气压缩机提供动力的空气,具体试验管道参数如表3所示。同时,使用NI-9215型号的采集板卡进行试验数据采集,优点是可执行差分模拟输入,实现了安全性、抗扰性的特点[14]。图7中,A,B处表示压电式声波传感器,用于采集管道实际信号。其中,将球阀一开一关用来模拟实际管道泄漏现象;敲击管道外壁用来模拟现场干扰状况。信号的采样频率为1 kHz,点数为10 000。

表3 管道实际参数Tab.3 Actual parameters of pipelines

图8示出原始泄漏信号时域波形,图9示出利用中心频率法确定VMD的参数K后,对原信号进行分解所得IMFs波形及频谱图。

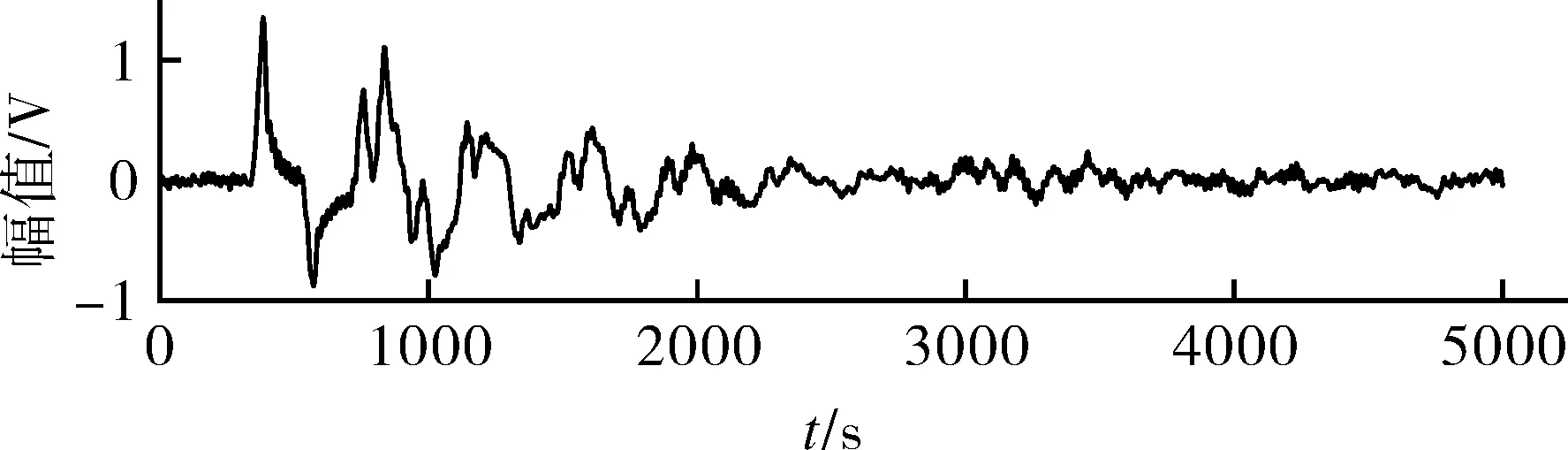
图8 原始泄漏信号时域波形Fig.8 Time domain waveform of the original leakage signal

图9 VMD分解所得IMFs波形及其频谱Fig.9 Waveform and spectrum of IMFs obtained from VMD decomposition

图10(a)示出马氏距离分布图,可以直观地看出,IMF5,IMF6之间的斜率最大,因此确定重构信号是由原信号去掉IMF5,IMF6所构成。图10(b)示出该去噪方法对信号的还原效果对比图。可以看出,VMD-MD方法能够有效地将有效模态与无效模态分离开,并且能够高度还原原信号的波形,只在2 100～2 500 Hz区间的波形幅值有少量差异,可以忽略不计。

(a)马氏距离分布

(b)还原效果对比图10 马氏距离分布及还原效果对比Fig.10 Distribution of Mahalanobis distance and comparison of reduction effects

为了证明本文所提去噪方法的有效性,图11示出实际信号的频域波形图。图12示出4种去噪方法所得重构信号的时域、频域波形图。在时域方面,EMD-HD所生成的重构信号整体幅值较小,波形整体失真严重;VMD-HD方法的还原效果较好,只在信号低频部分的幅值较小;VMD-BD 方法对于原信号的还原效果最差,整体波形都产生失真;而VMD-MD方法的还原效果优异,无论在低频部分还是高频部分,其波形趋势均与原信号保持一致。在频域方面,主要对比的有偏差的区域为频谱图中500 Hz处,实际信号在此有明显的能量峰值及能量下降趋势,而经过EMD-HD方法去噪后该能量下降趋势同样被去除,只保留少量能量幅值,即未保留原信号的特征;同样地,VMD-BD去噪后不仅去除了原始能量趋势,而且将此处能量幅值也同样去除,这也会导致波形出现大量失真。而VMD-HD与VMD-MD方法所得到的重构信号的频谱图表现优异,几乎还原了原信号的频域状态。

图11 实际信号的频谱Fig.11 Frequency domain waves of actual signals

(a)EMD-HD

(b)VMD-HD

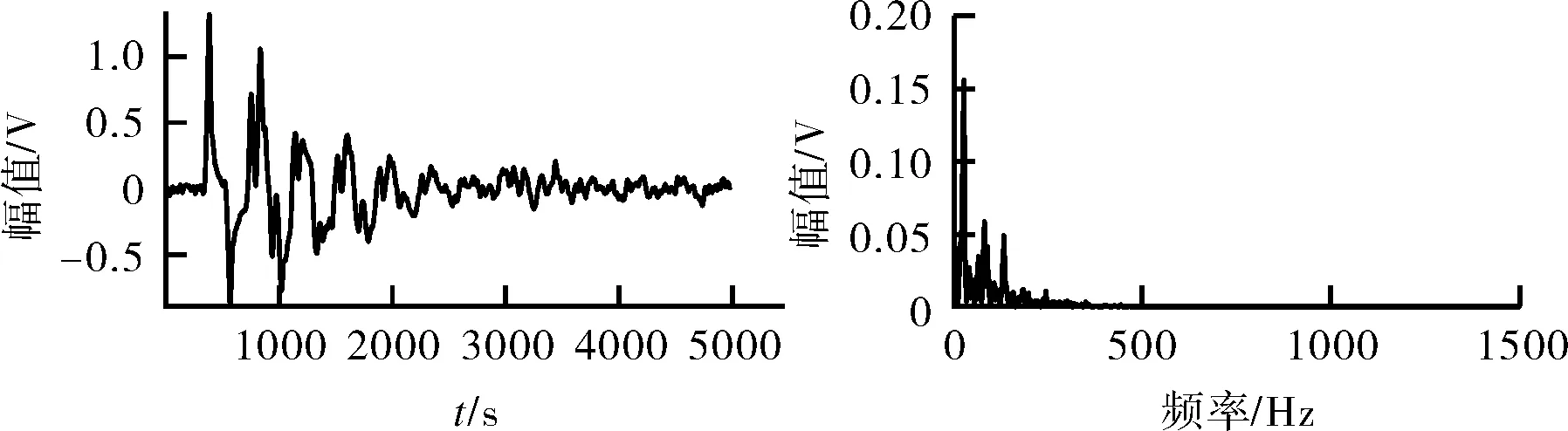
(c)VMD-BD

(d)VMD-MD图12 4种去噪方法所得重构信号时域、频域Fig.12 Time and frequency domain maps of reconstructed signals obtained from four denoising methods

然而,由于实际信号成分未知,只能通过频谱分析的方法来分析测量信号中的信号频率组成成分,又通过试验和前人分析可知,实际工程的信号为非平稳和非线性的信号,且信号中有效信号为低频信号,而噪声信号为高频信号[15],这样的分析导致试验结果会出现一定的局限性和不确定性。

此外,为了进一步对比VMD-MD方法的去噪效果,本文采用在信号处理中通常使用的均方误差(MSE)和信噪比(SNR)进行衡量[16]。MSE为预测结果与实际数据差的平方,其数值愈低,则预测的能力愈强;而SNR则为有用信号的功率与原信号的比值,其比率愈高,则表示该信号的去噪效果愈佳。定义式如下:

(10)

针对本试验的去噪性能指标MSE和SNR的数据如表4所示。

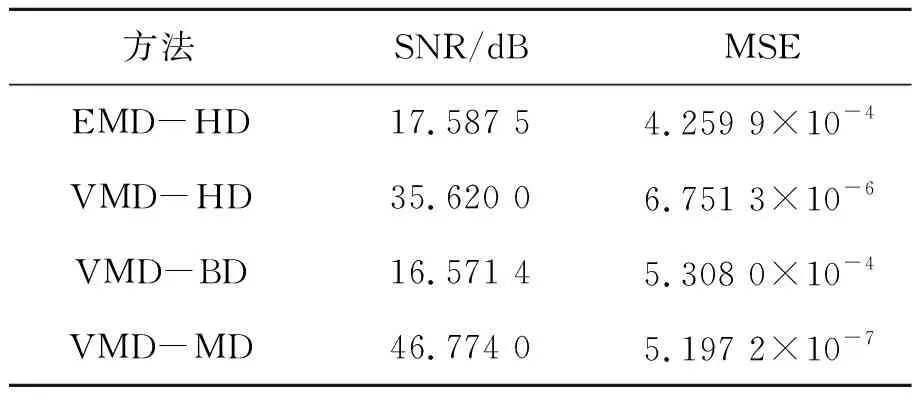
表4 去噪性能指标对比Tab.4 Comparison of the denoising performance indicators

从表4可以看出,EMD-HD和VMD-BD方法对信号去噪后的SNR为17.587 5,16.571 4 dB,MSE对应的为4.259 9×10-4,5.308 0×10-4,显然这两种方法的去噪效果并不理想,进一步验证了图12中所示的对原信号的还原效果较差。同时,虽然图12显示VMD-HD的还原效果较好,不过相较于VMD-MD所对应的46.774 0 dB和5.197 2×10-7来说,其对应的SNR为35.620 0 dB,MSE为6.751 3×10-6,效果较差。

综上所述,本文所提出的针对油气管道泄漏信号的VMD-MD去噪方法经过还原性对比试验及去噪性能指标衡量,效果均好于其余3种热门去噪方法,表明该方法的优越性。

5 结语

为了解决管道泄漏信号中包含噪声信号干扰的问题,本文提出了变分模态分解和马氏距离相结合的去噪方法(VMD-MD)。将该去噪方法应用到仿真信号和实际管道泄漏信号上,并采用SNR和MSE两个评价指标进行去噪效果评价,试验结果表明,通过与EMD-HD,VMD-HD,VMD-BD 相比,VMD-MD方法可以更加准确地分离出有效分量和噪声分量;同时,该方法具有较高的SNR和较低的MSE,从而更有效地实现信号降噪的目的,而且在滤波效果和对原始波形的还原度方面均凸现该方法的优越性。其主要结论概括如下。

(1)该方法利用马氏距离度量各个模态分量与原信号的相似性,可以减少失真程度。

(2)在两类试验中,该方法的还原效果明显好于其余三种对比方法。

(3)在实际管道试验中,增加去噪性能指标进行评判,该方法提高了信噪比,降低了均方误差,进一步验证其优越的去噪能力。

因此,本文所提去噪方法具备一定的研究价值,并且能够为下一步的信号分类、识别提供帮助。