大跨钢箱拱桥吊索长度精确计算方法研究与优化

刘龙飞，孙 元

(1.广西职业师范学院土木建筑工程学院,广西 南宁 530004;2.广西新发展交通集团有限公司,广西 南宁 530004)

钢箱提篮拱桥具有造型美观、跨径大、结构轻以及材料强度高等优点[1-3],不仅能改善平行拱的静力图式[4],还具有良好的动力性能、横向刚度[5]及整体稳定性[6],在实际工程中应用越来越广泛,例如跨径为130 m的澜沧江小湾大桥[7]、主跨550 m的上海卢浦大桥[8]、跨径58 m+208 m+58 m的厦门五缘大桥、主跨300 m的广西南宁大桥以及主跨为307.8 m匈牙利多瑙河大桥等。随着钢箱提篮拱桥的快速发展,出现了越来越复杂的截面、结构形式,施工精度也愈来愈被重视[9]。吊索作为钢箱拱桥关键的受力构件之一,其长度计算方法是否精确直接关系到桥梁的安全性和适用性。

吊索长度的计算方法与主拱的状态密不可分,通常基于三维有限元模型建立主拱的状态预测模型,以此来确定主拱的状态,预测模型相关的研究也比较多[10-15],例如回归预测模型、灰色预测模型[16]、AR预测模型、ARNA预测模型和DGM(1,1)预测模型等[17-18],也有学者[19-20]针对这些模型进行了优化,提出了优化的状态预测模型,取得了良好的效果。在确定主拱状态预测准确性的同时,保证吊索计算方法的准确性就成了至关重要的问题。一般而言,大跨钢箱提篮拱桥拱肋拱轴线迹点并不是截面形心,且大多为有倾角的变截面,无疑加大了吊索长度计算的难度,另外某些大跨钢箱提篮拱桥拱肋设计要求不设置预拱度,需要根据预测模型预测成桥线形,增加了吊索长度计算的难度。现阶段,国内大部分学者主要集中在悬索桥吊索长度研究,例如:祝长春等[21]通过研究理论荷载、实际荷载的影响,并对箱梁、索夹重量和数量进行统计,同时基于桥面铺装重度、缆索系统钢丝的实验,得到的吊索长度更为精确;姜军等[22]通过预测主缆线形的方法,较为准确的预测了悬索桥的吊索长度;贾一全等[23]一方面基于传统的归一化原理影响矩阵法优化了吊索索力,一方面给出了较为准确的吊索长度计算理论,但未考虑温度影响;向伟等[24]虽涉及钢箱提篮拱桥的吊索长度计算及过程,但仅从理论出发,未考虑现场实际情况,因此其计算结果误差较大。综上,国内缺少钢箱提篮拱桥吊索长度精确计算方法的相关研究。

为此,文章以计算跨径为457 m的某大跨钢箱提篮拱桥工程为依托,基于理论分析和数值模拟[25],同时结合现场实测复核的方法,提出了考虑温度影响改进的基于归一化原理的影响矩阵法,并对吊索索力进行优化,然后基于索力优化提出了吊索长度的精确计算方法。为同类型桥梁解决吊索预测长度与成桥状态存在偏差较大的问题,提供了借鉴和参考。

1 钢箱提篮拱桥吊索计算理论

1.1 预测模型建立

预测模型的建立对吊索的计算精度至关重要。通过对目前常用预测模型的对比分析,本文选用DGM(1,1)预测模型,由文献[11]中可知DGM(1,1)预测模型精度影响因素包括初始值x(0)(1)和参数β1,β2。因此,本文采用以下步骤建立预测模型:首先采用卡尔曼滤波法对原始序列进行预处理,优化参数β1,β2,其次引入修正系数λ抵消初始值x(0)(1)带来的偏差,最后将优化后的DGM(1,1)模型的预测结果与已知实测值进行比较,判断优化后的DGM(1,1)模型预测精度是否满足要求。

1.2 吊索计算理论

1.2.1 有应力长度计算

1)上锚固点坐标:对于截面形心,一般取截面几何中心,但拱肋轴线由特定荷载情况下的压力线决定。对于钢箱拱桥而言,拱轴线一般并不是截面的几何中心。因此,可以通过控制点的坐标(xk,yk,zk)或拱轴线迹点的坐标(x1,y1,z1),结合图1所示的几何关系得到上锚固点的坐标(xs,ys,zs):

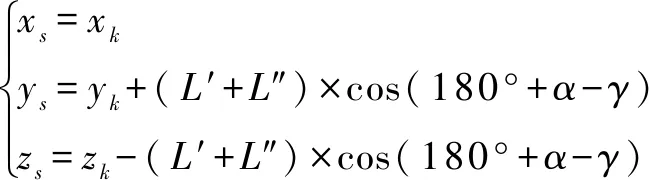
(1)

其中,L′为拱轴线迹点到吊索上锚固点的直线距离;L″为截面控制点到吊索上锚固点的直线距离;α为拱肋的内倾角;γ为吊索与y轴之间的夹角。假设拱肋为均质弹性体,模型成桥状态下拱肋的变形为(Δx,Δy,Δz),则可得到成桥状态下的吊索上锚固点的坐标(x′,y′,z′):

(2)

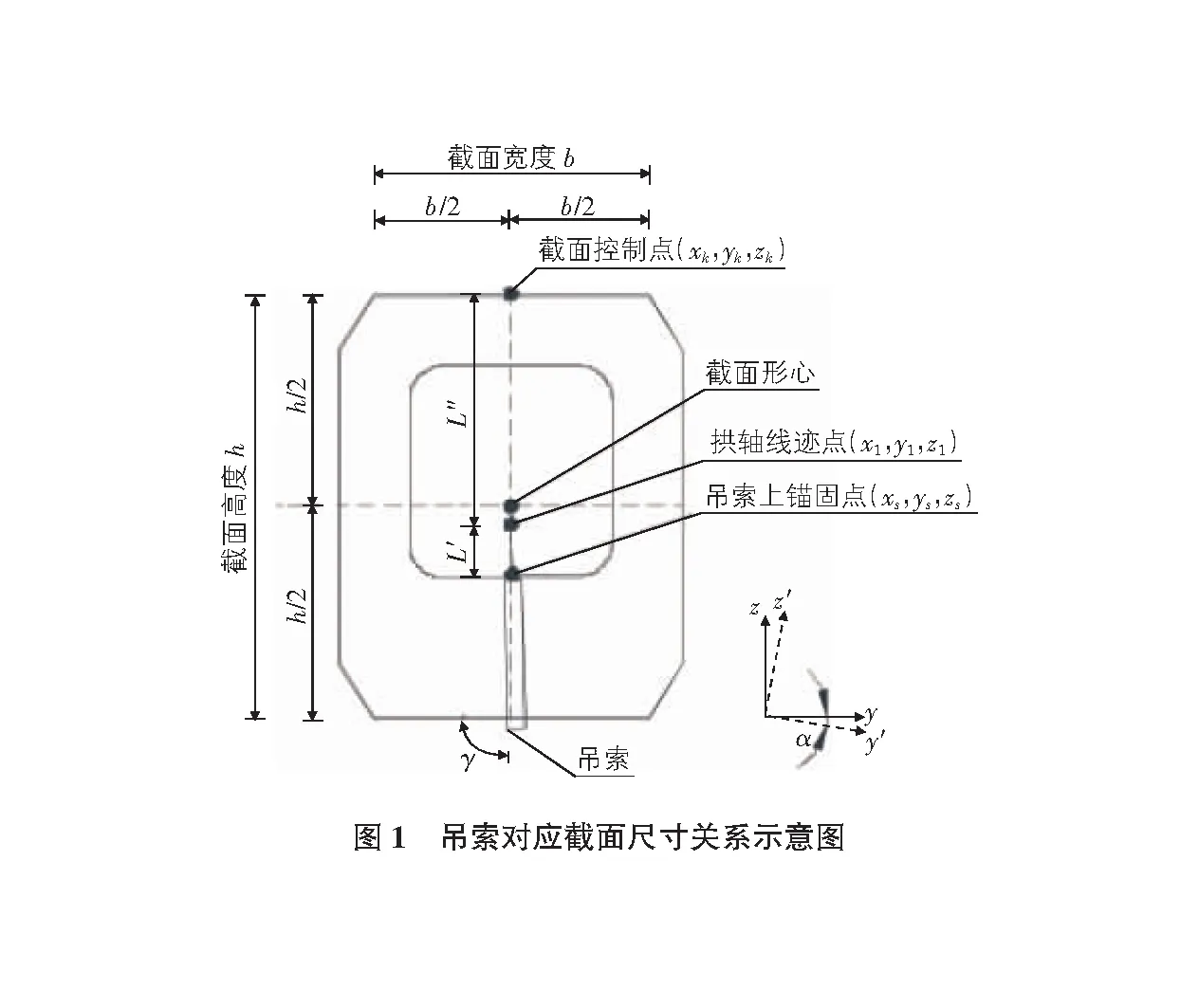
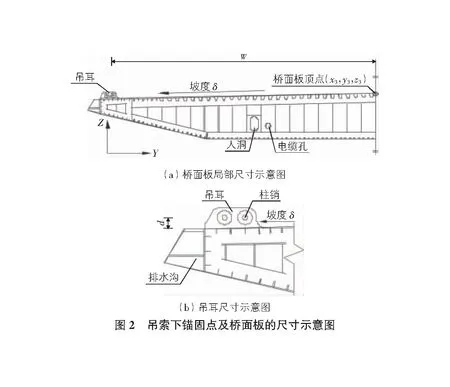
2)下锚固点坐标:根据图2所示的桥面坡度δ、桥面板顶点坐标(x3,y3,z3)、柱销的中心至桥面的距离d与吊索下锚固点坐标(x″,y″,z″)之间的几何关系,可得:

(3)

3)有应力长度L1:根据式(2),式(3)分别得到上锚固点坐标(x′,y′,z′)、下锚固点坐标(x″,y″,z″),再由两点间的距离公式即可得到有应力长度L1:

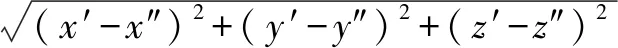
(4)

1.2.2 弹性伸长量计算

一般来说,大跨钢箱提篮拱桥的吊索位移很小,但应力较大。因此,根据Ernst公式吊索的弹性模量受力过程中不变[26]。为简化计算,可做如下假设:1)单个吊索中的每束钢束受力均匀;2)单个吊索中的每束钢束伸长量相同。可得到吊索弹性伸长量的计算公式:

(5)

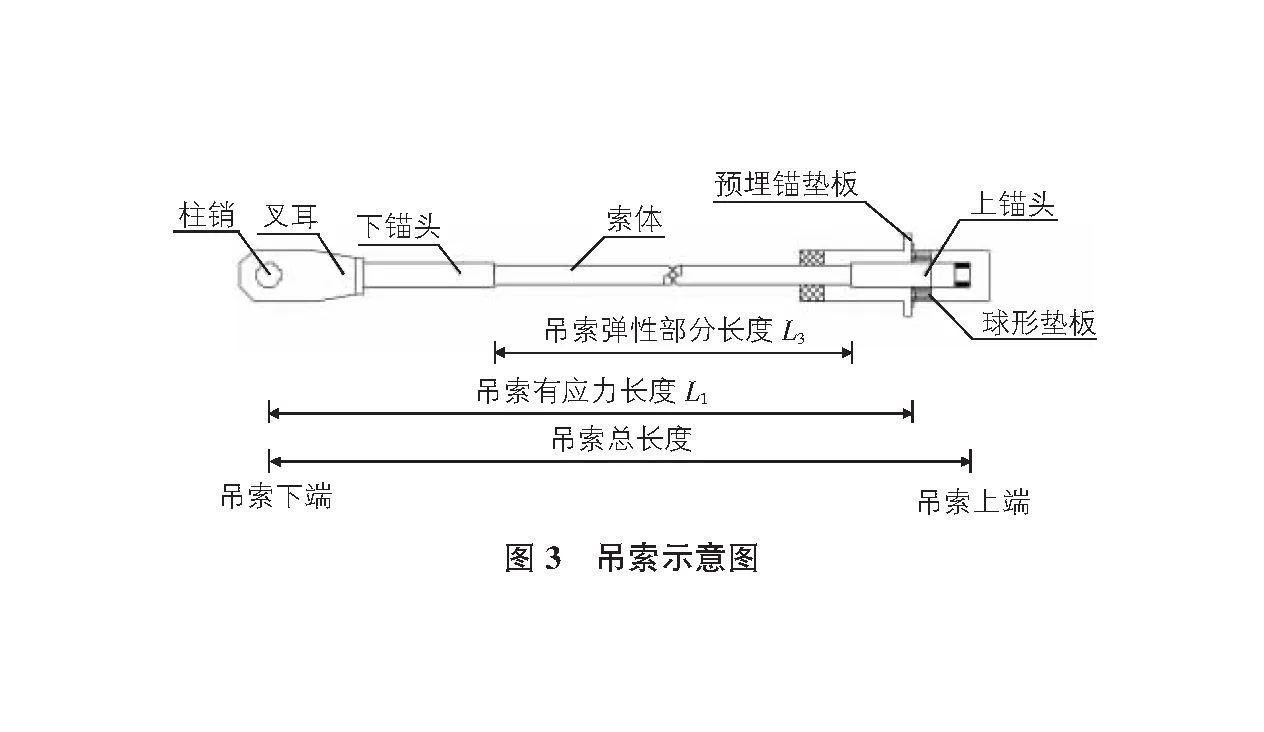
其中,ΔL为吊索的弹性伸长量,mm;N为优化后的吊索索力,kN,包含吊索和桥面板自重引起的轴力、二期恒载按刚度分配至各吊索上的轴力;L3为吊索弹性部分的长度,mm,根据L3=L1-L2计算;L1为吊索长度,mm;L2为修正长度,mm,包括:上锚头长度和下锚头长度以及上锚头到预埋锚垫板的距离,如图3所示;n为计算吊索的钢束总数;E为计算吊索的弹性模量;A为计算吊索的横截面面积,mm2。

从式(5)可以得到,精确的索力对吊索的计算精度有至关重要的影响。实际工程中,温度等各种因素对索力有比较大的影响,因此基于目前的研究成果[27],考虑温度荷载效应对传统的基于归一化原理的影响矩阵法加以改进,实现索力的优化,过程如下:

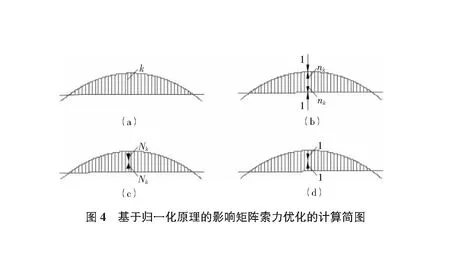
1)假设某桥有吊索m个,随机选其中某一编号为k的吊索,如图4(a)所示,在索长方向施加单位力1,如图4(b)所示。通过有限元分析可得各吊索的内力矩阵n(k)=[n1n2…nk…nm-1nm]。

2)设Nk=1-nk,施加于k吊索,同时取消k吊索上的单位力1和内力nk,此时k吊索内力为n(k′)=[n1n2…Nk…nm-1nm],但其他吊索的内力、位移均无改变,如图4(c)所示;然后对图4(c)状态下的结构内力乘以1/Nk进行归一化处理,可得到k吊索索力调整后的影响矩阵:

ΔN(k)=
[n1/Nkn2/Nk… 1 …nm-1/Nknm/Nk]

(6)

3)由1),2)步对每个吊索进行归一化处理,得到各吊索索力调整后的影响矩阵:

δN=
[ΔN(1)ΔN(2)… ΔN(k)… ΔN(m-1)ΔN(m)]T

(7)

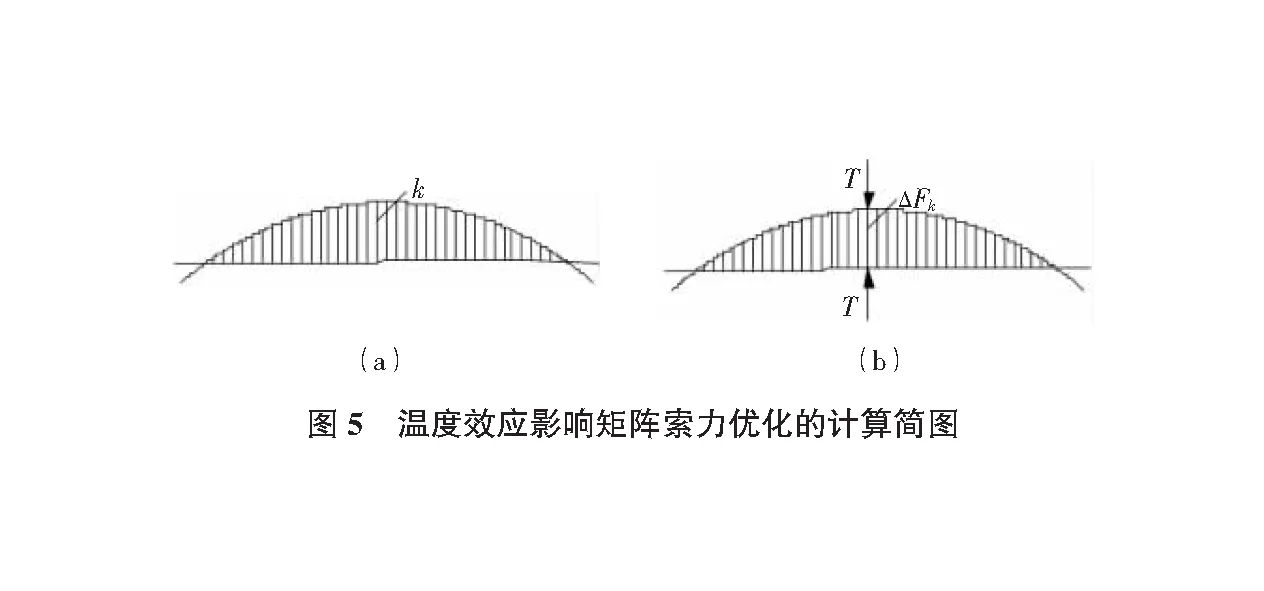
4)考虑温度荷载T(k)对吊索k的影响,计算可得到各吊索内力变化矩阵Δf(k)=[ΔF1ΔF2… ΔFk… ΔFm-1ΔFm],如图5所示,经过量化处理,得到温度对吊索k的影响矩阵:

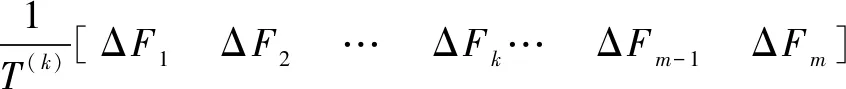
(8)

同理,对各个吊索进行处理,得到温度的影响矩阵:

δT=
[ΔF(1)ΔF(2)… ΔF(k)… ΔF(m-1)ΔF(m)]T

(9)

5)对原始索力N0进行调整:

N=δT·ΔT+δN·ΔN+N0

(10)

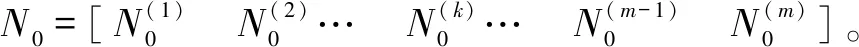
1.2.3 无应力长度计算

根据计算得到的吊索有应力长度L1及吊索弹性伸长量ΔL,根据式(11)得到吊索无应力长度:

L=L1-ΔL

(11)

2 工程算例

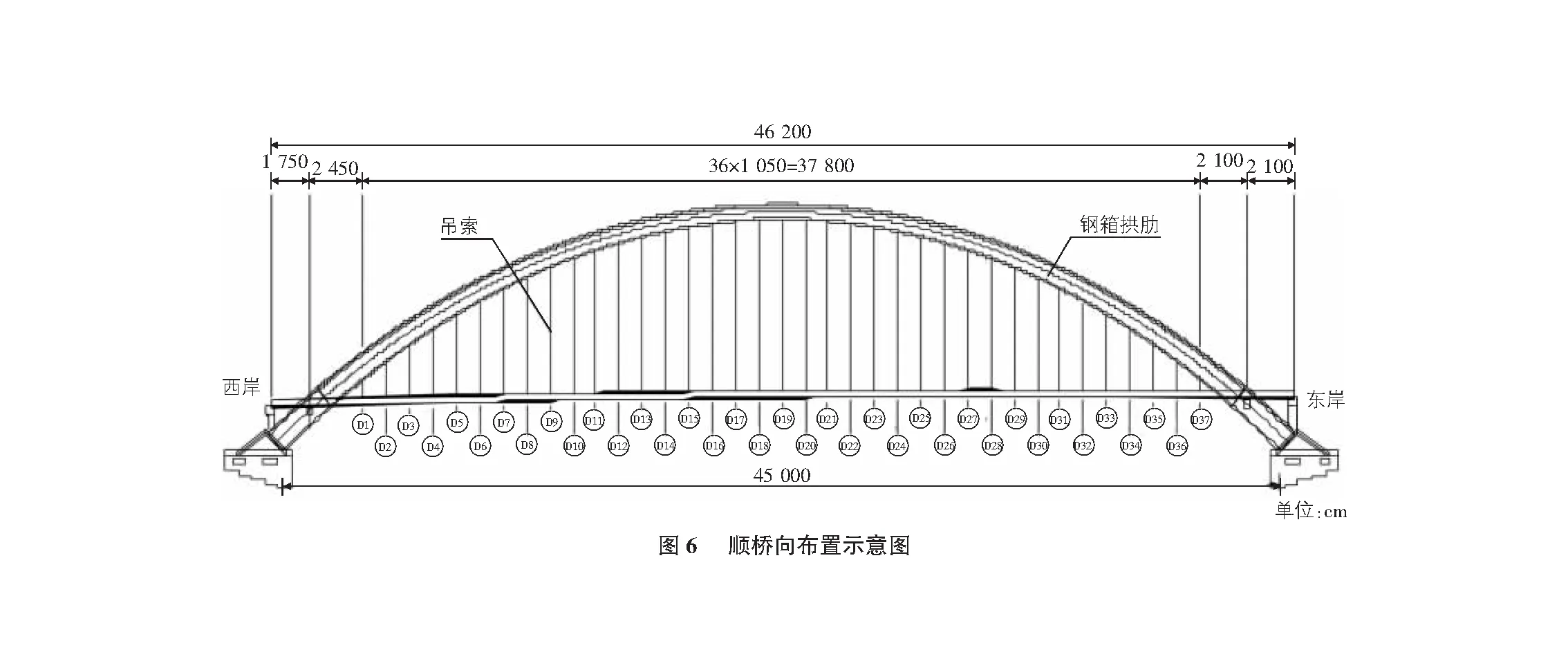
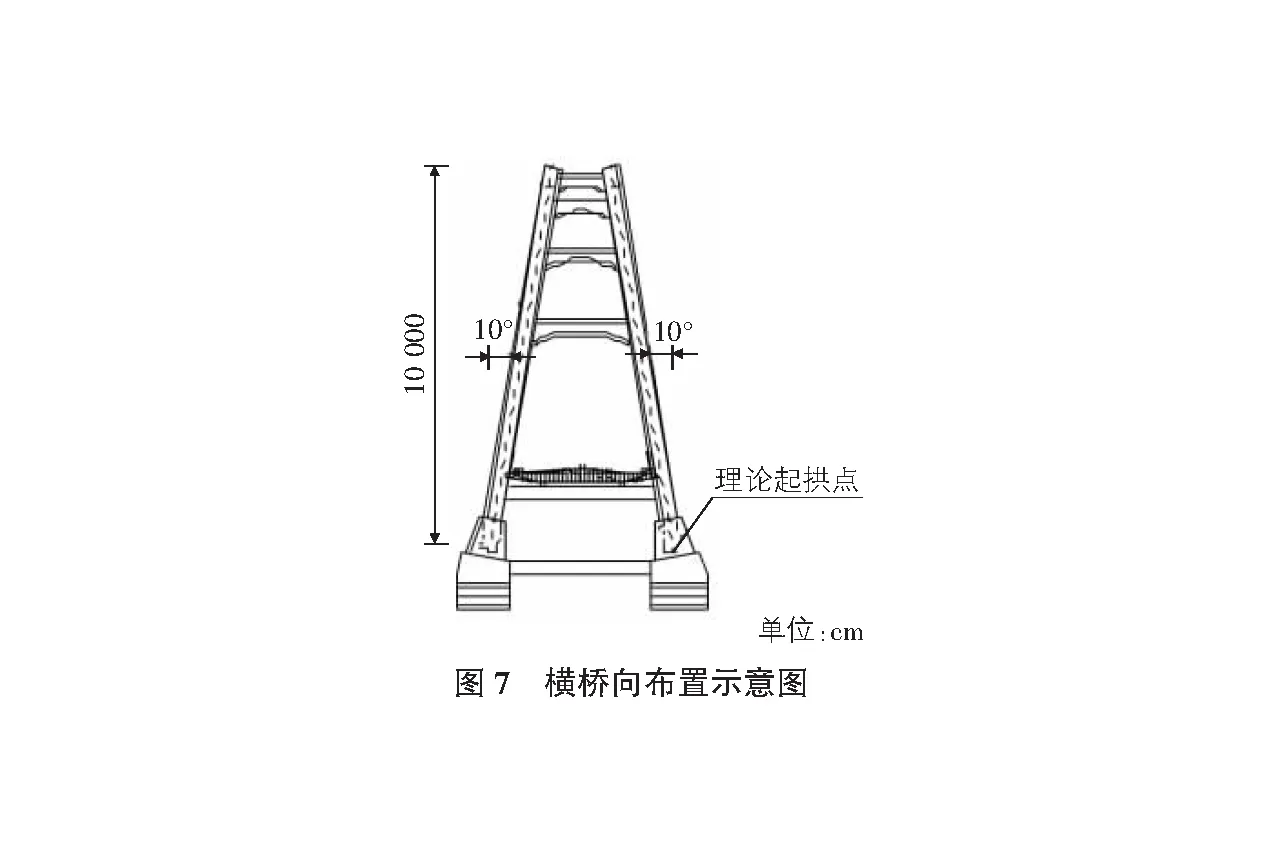
某大跨桥梁为有推力的钢箱提篮式拱桥,其主桥全长462 m,桥梁有效宽度为39.5 m,双向六车道。主拱计算跨径为457 m,净跨径为450 m,净矢高为100 m,矢跨比为1∶4.5;主梁跨径布置为(17.5+24.5+36×10.5+21+21) m,钢箱拱肋采用等宽变高的单箱单室截面,拱平面与竖直平面的夹角为10°,桥面板采用单箱单室扁平流线型全焊钢箱梁。吊索采用1860钢绞线,其中单根钢绞线直径15.2 mm,面积140 mm2。分别对吊索进行编号,如图6,图7所示。按施工要求,吊索可调节范围±2.0 cm,因此必须要精确计算吊索长度。

3 模型概况

3.1 模型简介

建立MIDAS/CIVIL有限元模型,其中节点共有2 586个,单元3 675个。拱肋、桥面钢箱梁均采用梁单元,吊索采用受拉单元中的桁架单元,其中拱肋钢箱梁、桥面板分别采用Q370qD钢、Q345qD钢及Q235,钢材弹性模量为2.06×108kN/m2,泊松比为0.30,容重为76.98 kN/m3;吊索采用1860钢绞线、HRB400级钢筋,弹性模量为1.95×108kN/m2,泊松比为0.30,容重为78.50 kN/m3;填充混凝土等级为C50,其弹性模量为3.45×107kN/m2,泊松比为0.20,容重为25.00 kN/m3。拱肋单元划分时吊点必为单元划分点,其余以每2 m～3 m为一个划分单元,桥面钢箱梁以每3.5 m为一个单元,有限元模型如图8所示。

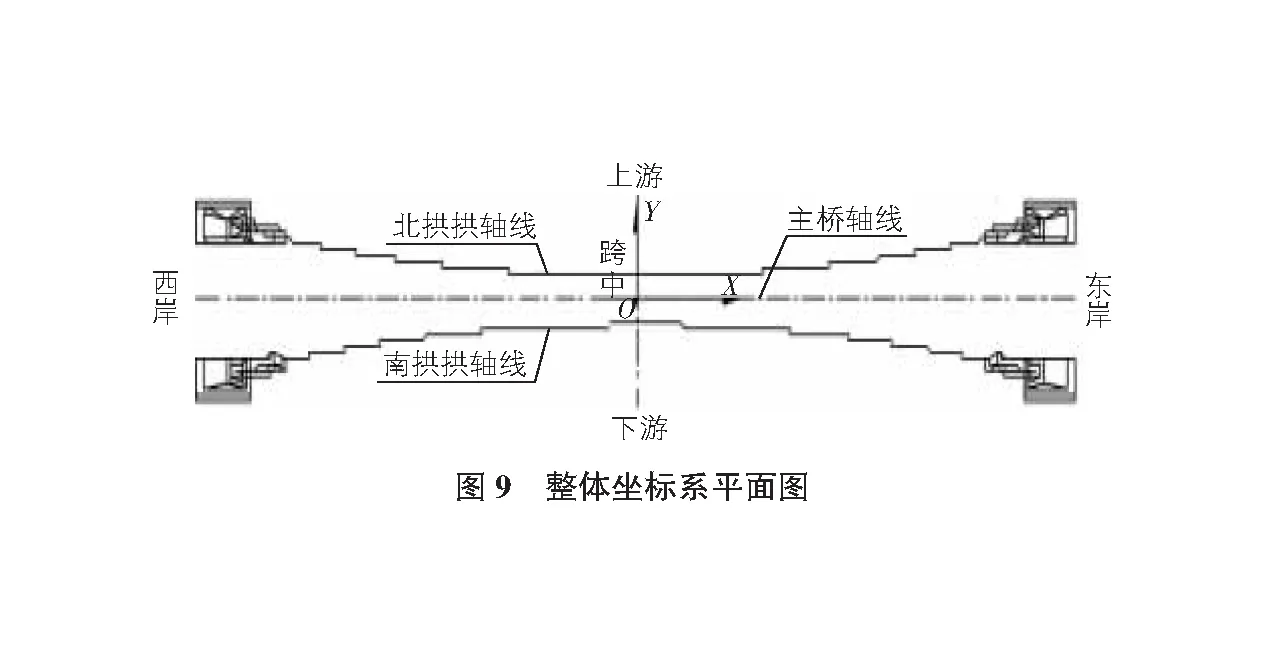
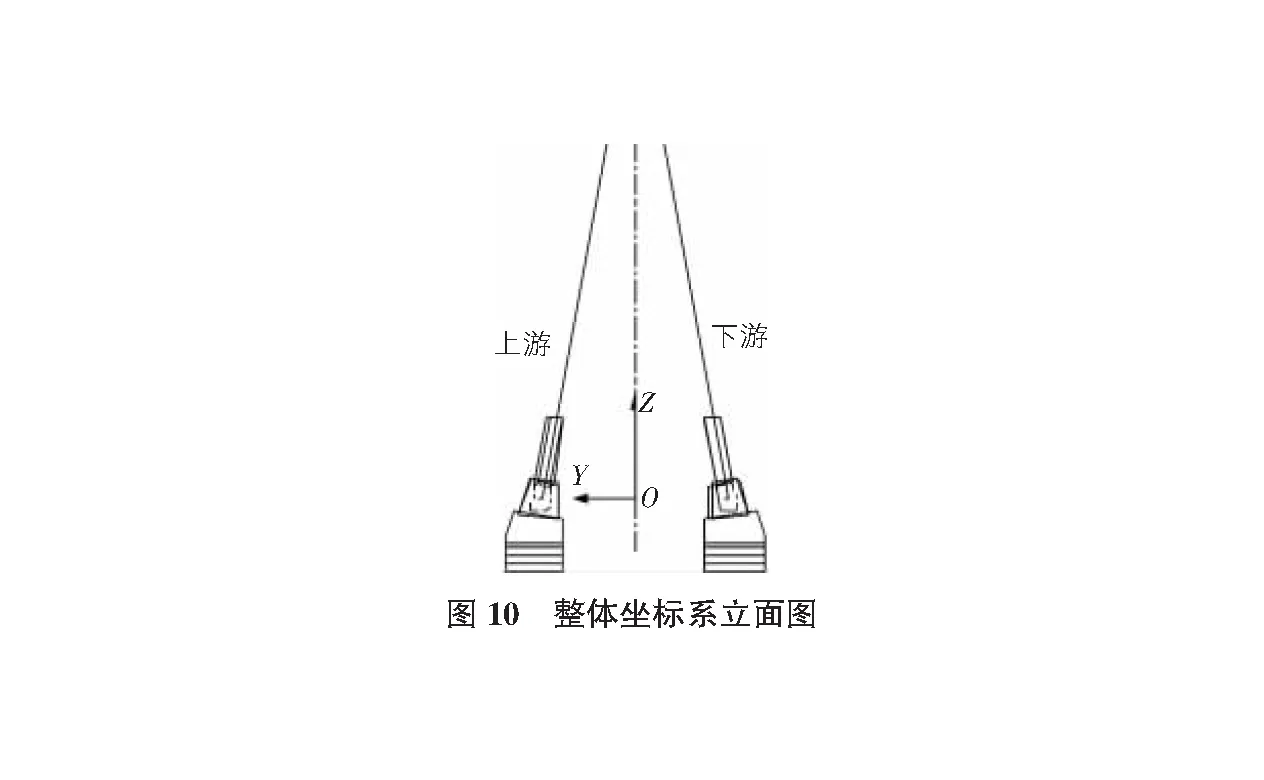
模型的约束条件为:拱脚采用固定边界;吊点与主体结构采用刚性连接。为了方便,运用等效截面的方法以单索代替实际工程中的双索进行模拟。建立整体坐标系,如图9,图10所示。

3.2 荷载概况

成桥状态下,吊索的变形主要受到吊索自重、桥面板节段自重和二期恒载的影响。根据实际统计,桥面板自重为68 922.14 kN,横隔板自重为23 076.40 kN,总重为91 998.54 kN,而模型桥面板及横隔板自重为79 143.94 kN,所以索力计算时重力系数采用91 998.54/79 143.94=1.16。人行道板、人行道栏杆、防撞护栏、水密门、竖向支座加劲、锚块、阻尼器、排水槽以及7.00 cm沥青铺装层共重33 871.37 kN,按二期恒载73.31 kN/m施加于桥面板上。

4 计算结果分析

4.1 预测模型分析

将合龙口连续观测的变形量作为初始数据,然后根据文献[20]得到参数β1,β2分别为1.1,-14.5,修正系数λ为1.18,进而建立优化后的DGM(1,1)预测模型,根据已测数据进行拟合得到:

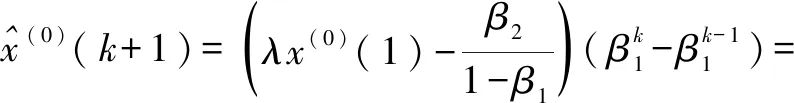
(12)

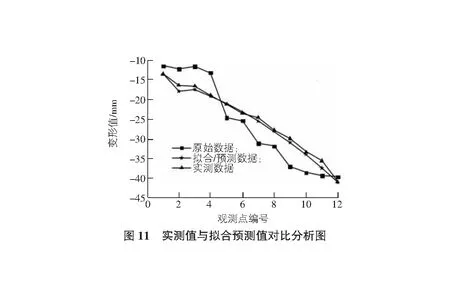
基于式(12)并对结构状态进行预测,结果见图11。由图11可以得到,原始数据与实测数据的残差最大值达到了7.2 mm,而预测数据残差最大值仅为-1.8 mm;原始数据的残差百分比平均值为18.3%,远远大于预测数据的残差百分比平均值2.2%,因此优化后的DGM(1,1)模型能够准确的预测结构状态。

4.2 索力优化结果分析

根据改进的基于归一化原理的影响矩阵法对模拟得到的索力进行优化,其结果对比见图12。

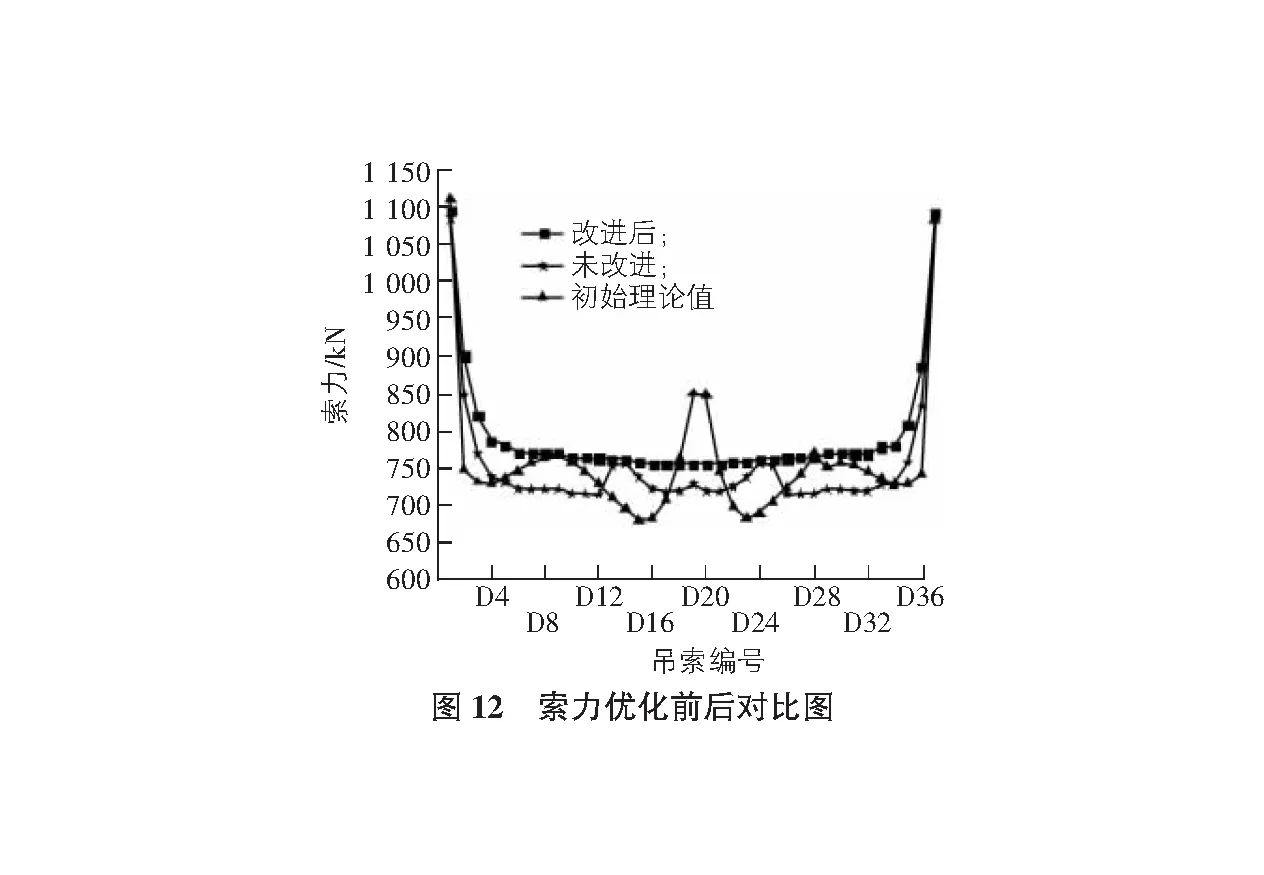
由图12可知:1)优化得到的索力最小值出现在中间位置,与设计更相符;2)优化后得到的索力曲线相较未优化的索力、初始索力理论值曲线更平顺;3)优化后索力标准差62.1 kN明显小于未优化索力标准差65.6 kN和初始索力理论值标准差72.3 kN,说明优化后索力分布更均匀。综上,采用改进的基于归一化原理影响矩阵法对索力进行优化,可以保证成桥结构受力更合理。

4.3 吊索长度结果分析

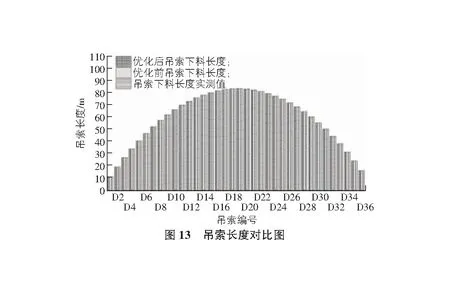
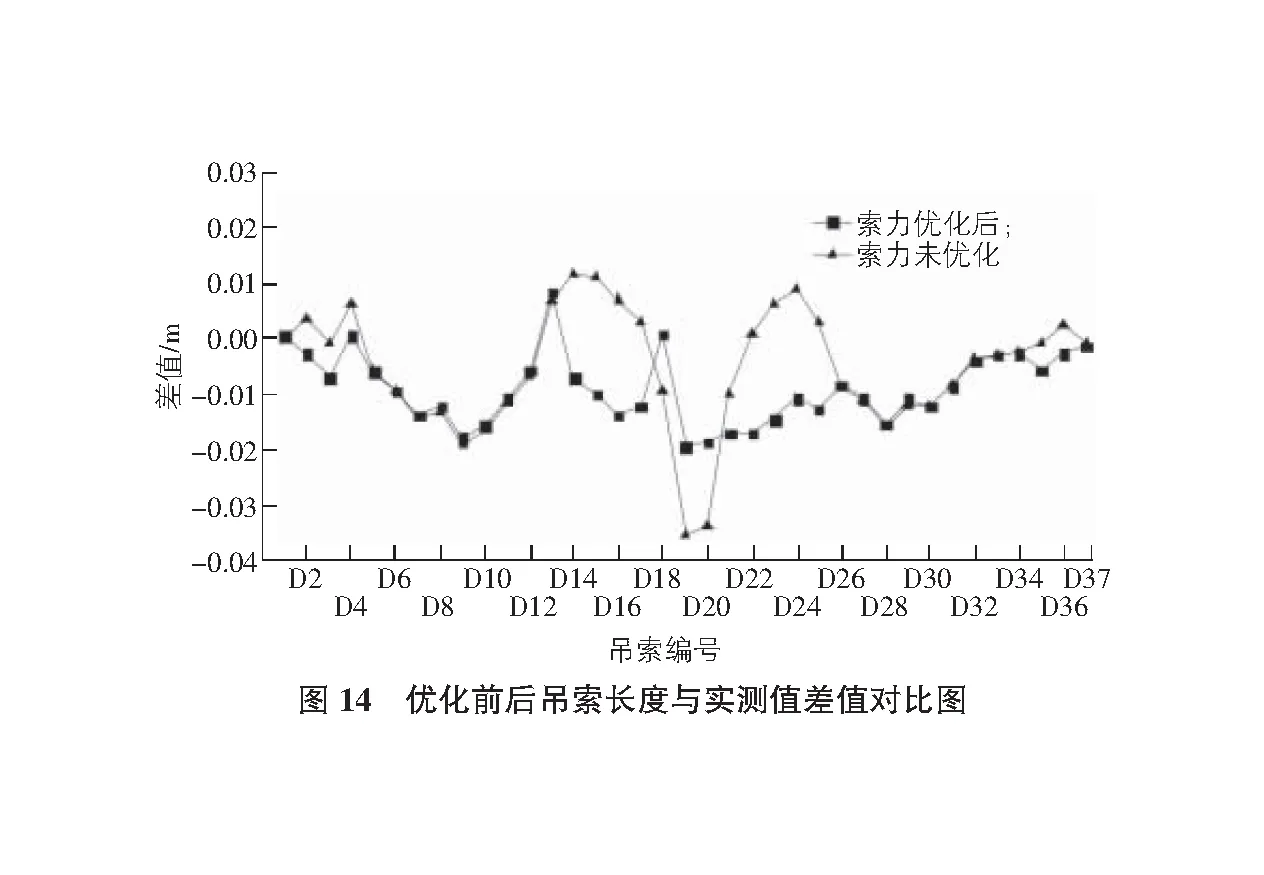
基于索力优化,同时结合吊索计算理论,可得该工程优化后的吊索长度。索力优化前后的吊索长度见图13,并将其与实测值进行了对比。为验证结果,分别将未优化的吊索理论长度、优化后的吊索理论长度与实测值作差,见图14,可得未优化、优化后的吊索理论长度与实测值的差值标准差分别为11 mm,6 mm。因此可以得出如下结论:1)优化后的吊索长度差值标准差6 mm明显小于未优化的吊索长度差值标准差11 mm,说明优化后的吊索长度与实测值更为接近;2)优化后的吊索长度差值均在施工精度要求的±20 mm范围内,但未优化的D19和D20吊索长度差值分别为36 mm和34 mm,不满足施工精度要求。因此,基于索力优化得到的吊索长度计算结果更为精确,与实际工程更为贴合。

5 结论

本文以计算跨径为457 m的某大跨钢箱提篮拱桥工程为依托,从实际工程、理论分析及仿真模拟出发,探求大跨钢箱提篮拱桥的吊索长度精确计算方法,主要结果和结论如下:

1)基于现场实测数据,建立了大跨钢箱拱桥的三维有限元模型以及主拱状态的优化DGM(1,1)预测模型,并对大跨钢箱拱桥的状态进行预测,结果表明预测模型原始数据残差百分比的平均值由18.3%降到了2.2%,最大值由30.4%降到了5.7%,优化后的DGM(1,1)预测模型具有较高的精度。2)考虑温度效应的影响,改进了基于归一化原理的影响矩阵法,利用改进的基于归一化原理的影响矩阵法对索力进行了优化,结果表明改进的基于归一化原理的影响矩阵得到的索力标准差为62.1 kN小于未改进得到的索力标准差65.6 kN,因此优化后索力更为均匀合理。3)根据优化后的DGM(1,1)模型预测成桥状态下的拱轴线线形,将索力优化前后的吊索长度与实测值进行了对比分析,结果显示优化后的吊索长度与实测值的差值标准差为6 mm,小于未优化的吊索长度与实测值的差值标准差11 mm,且优化后的吊索长度差值均在施工精度要求的±20 mm范围内,可为同类型桥梁的设计和施工提供借鉴和参考。