闭口流线型箱梁在施工阶段的涡振抑振措施研究

廖沛东

(山西交物路桥建设有限公司,山西 太原 030001)

0 引 言

随着交通建设的发展,桥梁跨径也随之不断增长,桥梁跨径越长,结构总体刚度越小,对风的敏感程度就越高,在特定风速下更容易产生风致振动[1]。涡振就是在低风速下某些柔性结构发生的振动现象。虽然涡振的振幅不会发散从而导致桥梁结构发生破坏,但对行车舒适性有很大的影响,长此以往势必会造成结构内部疲劳损伤。近年来许多大跨径桥梁都在使用阶段发生了涡振现象,因此对桥梁涡振的研究一直是桥梁风工程中的重要课题。

影响桥梁涡振的因素有很多,比如断面的阻尼比、结构的刚度、断面的气动外形等[2,3]。其中气动措施是通过改变桥梁的气动外形来改变桥梁附近的空气流动状态,从而降低桥梁涡振的一种方法,是最常用来降低桥梁涡振的措施。本文对某工程实例中主梁断面的气动外形进行研究,得到对于类似主梁断面的选型建议。

1 工程概况及动力特性

某大桥为主梁主跨800 m的双塔悬索桥,主梁断面为闭口流线型箱梁断面,主梁跨中断面高3 m,桥面宽度33 m,腹板角度为a,风嘴角度为b,见图1。

图1 主梁标准横断面尺寸

通过有限元软件Ansys计算结构的动力特性,得到后续数值模拟所需的结构频率,采用Beam4单元模拟桥梁的主梁以及桥塔等构件,采用Link10来模拟悬索桥上的主缆以及吊杆等构件,边界条件则按照桥梁实际情况来进行约束。其中,主梁的一阶反对称扭转的频率为0.32 Hz,一阶正对称扭转的频率为0.34 Hz。

2 CFD数值模拟

本文采用FLUNET进行数值模拟,选取+5°作为最不利风攻角[4],以断面的腹板角度a和风嘴角度b作为变量,腹板角度为10°、12°、14°、16°,风嘴角度为30°、40°、50°、60°,两两组合,共得到以下16个工况,见表1。

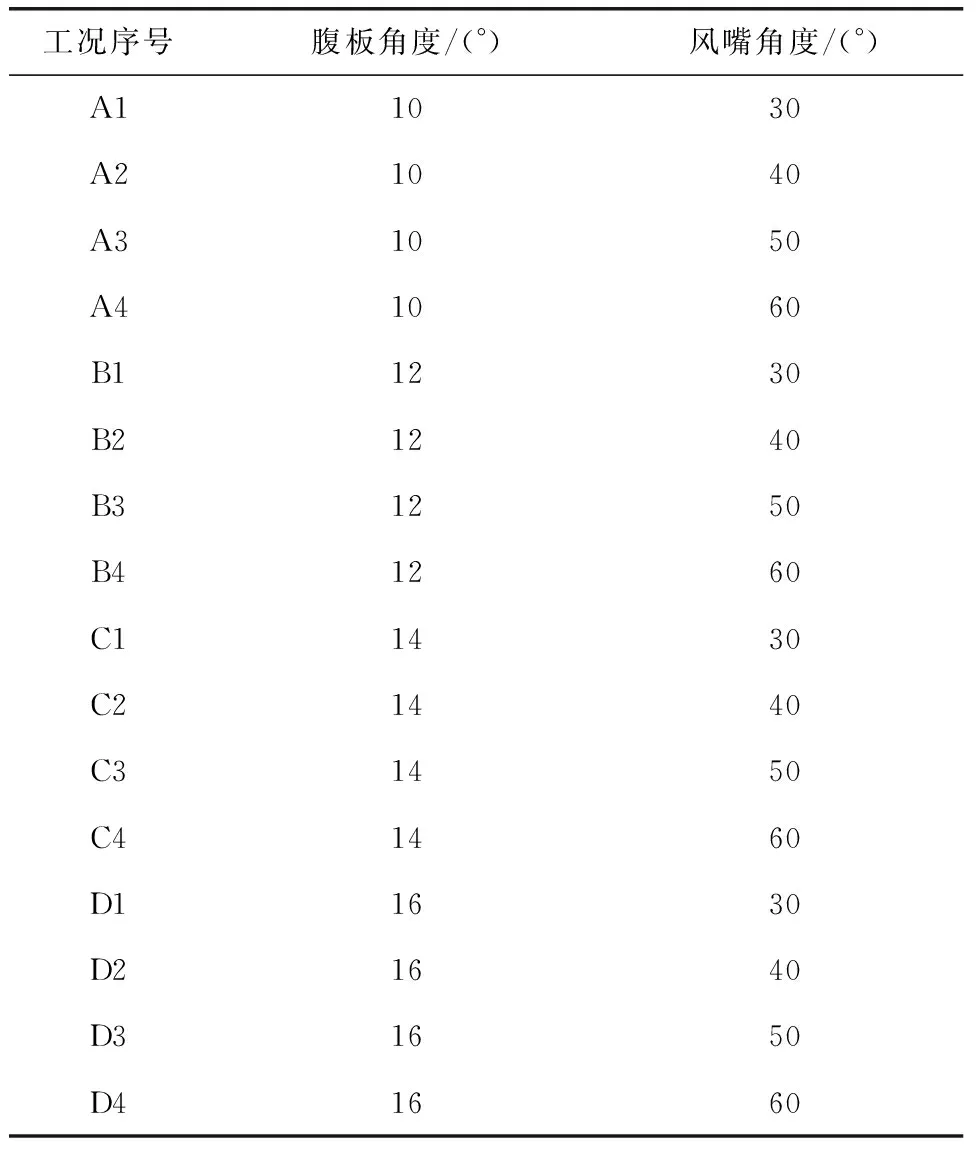
表1 数值模拟工况设置

由于三维网格计算量相较于二维模型成几何倍数增长,对设备要求较高,而二维计算模型也能保证良好的计算精度,因此本文采用二维模型来计算[5],计算模型无缩尺比,计算域形状为矩形,大小为20 B×15 B。左侧边界为速度入口,右侧边界为压力出口,上下边界为对称边界。网格划分为三个区域:最外侧区域FENG1为静止区域;最内侧区域FENG3为刚体区域,中间的FENG2为动网格区域,利用自由振动法求解扭转涡振的振幅。

网格采用三角形,在断面附近设置边界层,使Y+值小于1,湍流模型采用SST K-w模型,并利用UDF提取计算间隔时间断面的位移和角速度。网格总体数量约为30万个,为防止出现负网格或者网格畸变过大影响计算结果,在开始计算前设置网格畸变率监视,当运动过程中出现过大的网格畸变率时,利用网格重构技术来自动重新划分网格质量差的单元,保证计算结果的精度。图2中列出计算时部分工况的时程曲线,分别为腹板角度16°、风嘴角度为60°扭转涡振振幅最大的位移时程曲线,腹板角度10°、风嘴角度50°的扭转涡振位移时程曲线。

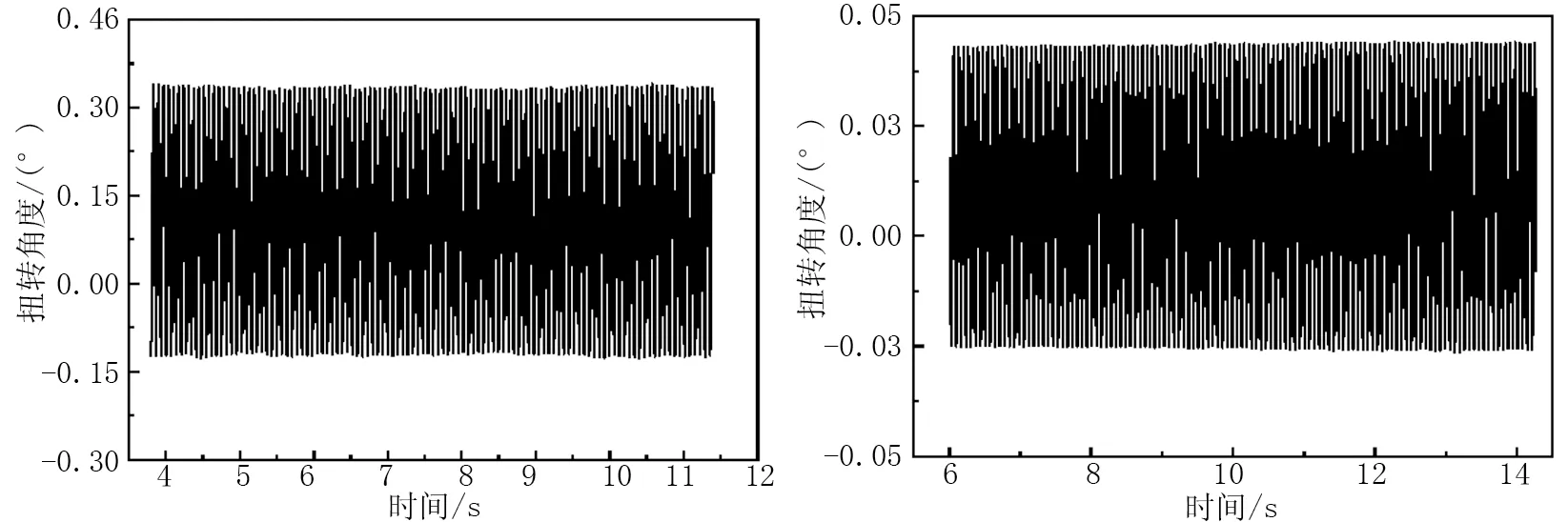
图2 扭转位移时程曲线

3 计算结果对比及机理分析

为了方便比较计算结果,使其更具有普适性,对风速进行无量纲化处理(即将风速与结构频率相除)。通过对表1中16个工况的时程曲线进行处理,得到在不同气动外形下断面涡振响应曲线,见图3。

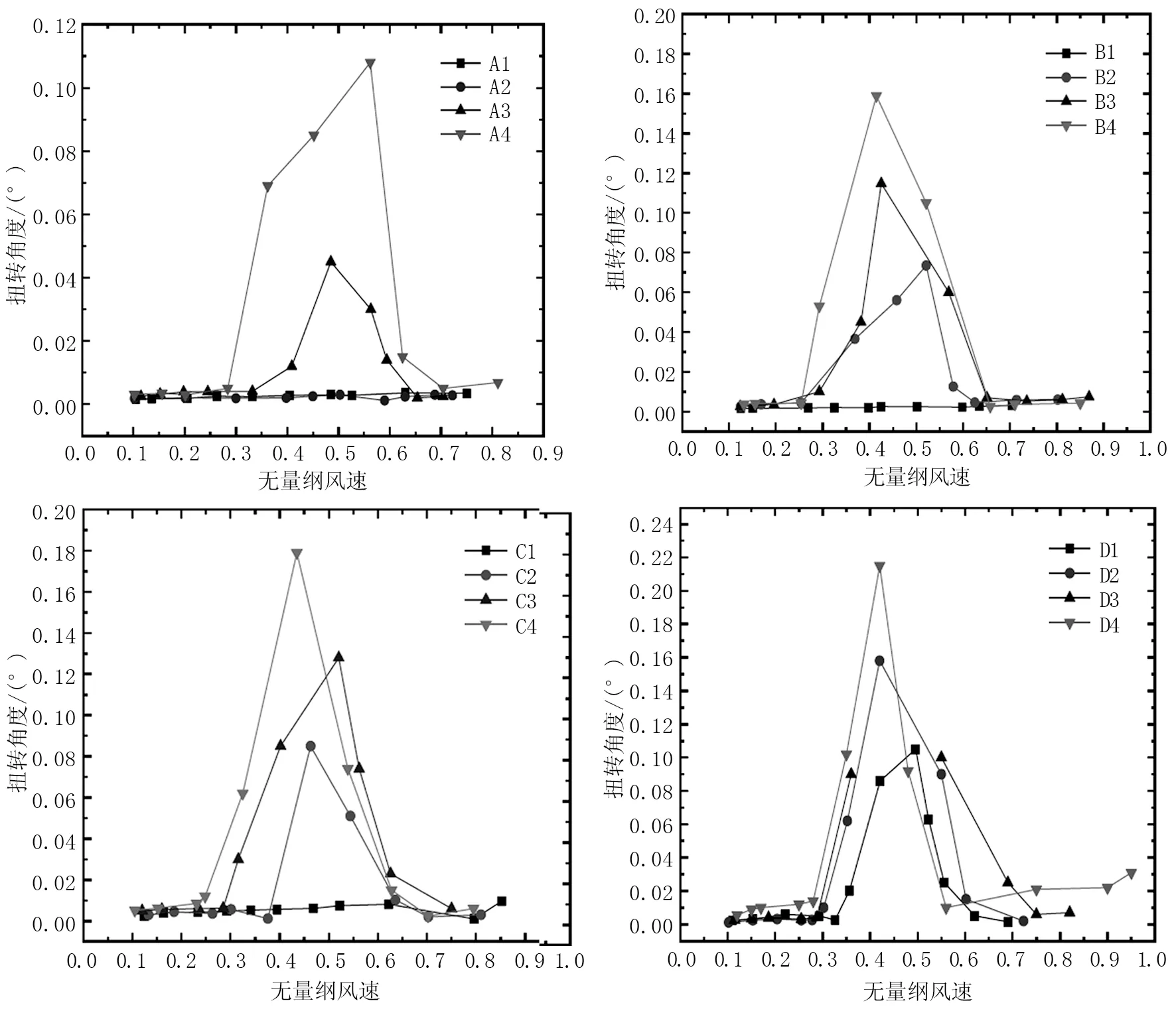
图3 不同气动外形下的涡振响应

3.1 风嘴角度对断面涡振影响分析

当腹板角度为10°,风嘴角度为30°和40°时断面没有发生扭转涡振。当风嘴角度增加到50°时,断面开始出现了扭转涡振,继续增加风嘴角度至60°,可以发现扭转涡振的振幅明显比风嘴角度50°时的振幅大两倍,而且起振风速也从0.409提前至0.362,涡振结束时的风速从0.594延长到0.625。

当腹板角度为12°,风嘴角度为30°时断面未发生扭转涡振,而断面风嘴角度增加至40°时开始发生扭转涡振。随着断面风嘴角度的不断增加,涡振时最大扭转角度从0.074增加到0.156,起振风速从0.369提前到了0.293,而锁定区间长度也从0.21延长至0.365。

当腹板角度为14°时,所有不同风嘴角度下的断面均发生了扭转涡振,随着风嘴角度的不断增加,所对应的断面扭转涡振响应就越大,且起振风速随着风嘴角度的增大而提前,从0.376提前至0.248,涡振的锁定区间长度越来越长,从0.26增加至0.38。

腹板角度为16°时与腹板角度14°时规律基本一致,不同风嘴角度下所有断面均发生了扭转涡振,随着风嘴角度的增加,扭转角度从0.105°增加至0.215°,起振风速从0.356降低到0.28,扭转涡振结束时对应的风速从0.576增加至0.7。

3.2 腹板角度对断面涡振影响分析

当风嘴角度为30°时,对比工况A-1、B-1、C-1、D-1可以发现,当腹板角度为10°、12°、14°时,断面未发生扭转涡振,仅在腹板角度为16°时发生了扭转涡振,最大振幅为0.105°,锁定区间长度为0.22。

当风嘴角度为40°时,对比工况A-2、B-2、C-2、D-2,断面仅在腹板角度为10°时未发生扭转涡振,在腹板角度为12°、14°、16°时均发生了扭转涡振,随着腹板角度的增加,扭转涡振的最大振幅从0.0735°增加至0.158°,起振风速从0.369提前至0.302,因此腹板角度越大,涡振响应就越大。

当风嘴角度为50°时,对比工况A-3、B-3、C-3、D-3,断面在不同的腹板角度下均发生了扭转涡振,涡振幅度随着腹板角度的增加而增加,其中最大扭转角度从0.045°增加至0.205°,锁定区间长度从0.185增加至0.41,起振风速从0.409降低至0.288。

当风嘴角度为60°时,对比工况A-4、B-4、C-4、D-4,与A-3至D-3四个工况一致,断面均在不同的腹板角度下发生了扭转涡振,但是A-4与A-3相比,扭转涡振更加明显。在风嘴角度60°时,随着腹板角度的不断增加,最大扭转位移从0.263°增加至0.42°,起振风速从0.362降低到0.28。

3.3 涡振机理分析

对比A-1和D-4两个工况可以发现,在风嘴角度和腹板角度均较大时,断面更容易发生扭转涡振;对比B-2和C-3两个工况可以发现,风嘴角度和腹板角度越大,断面涡振的响应就越大。

因此,在其他条件不变的情况下,断面的风嘴角度越大或者腹板角度越大,所对应的涡振效应就越明显。断面的外形越“钝”,气流吹过断面时越容易产生与结构基频一致的漩涡,从而引发结构产生涡振。反之,如果断面的气动外形越“光滑”,来流风流经断面时不容易被断面所分离,尾流处就不容易产生与结构频率相似的涡脱,进而不会导致主梁发生涡振现象。

4 结 语

通过对某工程主梁断面的最不利+5°攻角进行不同气动外形下的涡振数值模拟,结合各个工况下扭转涡振曲线的变化,分析涡振的形成原因,进而得到如下结论。

(1)在保证阻尼比等动力特性不变的情况下,闭口流线型箱梁的风嘴角度越小,断面越趋近于流线型,越不容易产生涡振。

(2)当结构阻尼比和风嘴角度不变时,减小腹板角度,也可以使断面趋近于流线型,从而保证断面具有良好的气动稳定性,更不易产生涡振。

(3)对产生扭转涡振的主梁断面,可以通过减少腹板角度和减少风嘴角度等气动措施来抑制涡振的产生,实验表明当两者相结合时的抑振效果更加明显。