基于微分观测器的飞行模拟转台伺服系统非线性控制
唐 苗,王海林,赵 慧,朱添麟,米俊宇,王 斌
(1.海装驻北京地区 第三军事代表室,北京 100074;2.航天科工防御技术试验中心,北京 100854;3.北京振兴计量测试研究所,北京 100074)
0 引言
现如今,时代在发展,科学水平已成了比较各国发展水平程度和在世界范围内影响力的重要指标。而国家军事国防水平是一个非常重要的指标,不容我们忽视的重要国家安全保障。航空技术在国家军事科技占据着突出重要位置,成为最高端的科学技术,是各国都极力去研究的领域。航天工程不仅提升国家工业生产链,也推动国家经济的快速发展。各国都想发展航天技术,因而得到更多科学家们去研究。推动航天技术发展,就一定要清楚惯导技术和制导技术,火箭成功发射需要该两个重要技术去支撑。惯导航技术和制导技术的作用是通过分析研究机械学、物理学和数学等几门重要学科来使得目标能够跟踪在所设计参考坐标系中的速度和位置等物理信息[1]。为了能够得到目标速度以及位置等重要信息,设计了加速度计以及陀螺仪等仪器,其作用是来对惯性导航系统定位精度进行测试,但加速度计以及陀螺仪需要用高精度的转台试验来对其核心元件进行测试标定[2]。因而,飞行模拟器转台是航天技术和国防技术等重要领域中不可缺少且具有较高复杂程度的高端设备。在第二次世界大战中,当时生产出来的导弹定位精度低,未能用大量实验来提高其精准度,因而作战效果小[3]。导弹具有的杀伤力大,限制了实验条件,为了能够提高导弹精度,可利用转台来进行半实物实验。飞行模拟器转台成本较低,可多次重复进行实验,节约了大量财力和物力。最重要的一点是飞行模拟器转台具有安全优点,在进行实验的过程中没有苛刻导弹条件,难度系数非常低。因而,飞行模拟器转台在军事领域里起到非常重要作用,还可节约成本和减小实验难度系数。雷达在我们生活中随处可见,转台是雷达伺服控制系统中非常重要的组成部分,转台性能决定着雷达控制系统的控制精度[4]。
飞行模拟器转台伺服系统是模拟导弹飞行的重要设备,方便得到实验数据。飞行模拟器转台是综合光学、机械电机学等学科的现代军事装备。在实验室环境条件下,其控制性能决定关系模拟实验可靠性优劣。飞行模拟转台伺服系统控制设计是保证系统控制精度。这里需考虑非线性摩擦部分,这会影响伺服控制系统控制精度及其稳定性[5]。
对飞行模拟器转台伺服系统的摩擦补偿和鲁棒跟踪控制进行了研究和实验。设计高性能飞行模拟器转台控制系统,需要使用高精度测量仪器和高效率的驱动元件以及合理的转台结构设计,更需要设计研究转台控制算法。飞行模拟器转台硬件电路确定以后,若提高飞行模拟器转台系统的精度,需设计鲁棒性强和控制效果优的控制算法。目前传统PID 控制算法、Smith 预估控制策略以及复合控制算法大量应用于飞行模拟器转台伺服系统中[6]。这些算法结构简单,理论分析成熟、满足简单控制系统的控制要求,成了普遍应用在大多数工业控制系统的算法。但这些算法需要建立在精确数学模型,要求数学模型精度高。而在实际应用过程中,飞行模拟器转台在高温高湿、高压高海拔等较为复杂的环境条件下,使得飞行模拟器转台会受到非线性因素影响。同时,飞行模拟器转台长时间工作过程中,可能会出现电机老化以及器件损坏等非线性因素[7]。这使得很难建立准确的飞行模拟器转台系统数学模型,传统控制方法应用在飞行模拟器转台可能达不到期望效果,若提高飞行模拟器转台系统控制性能,需研究新的控制策略。改进控制算法和研究其它控制算法在飞行模拟器转台系统中应用成了科学家一研究方向。
经典控制算法研究应用方面有一些新成果。西南交通大学幸权结合时域 PDF(伪微分反馈)策略与频域 PDF 方法,使用基于特征根结构理论的能量量化法,提出基于 PDF 控制策略的最优频域设计方法[8]。黄金泉分析飞行模拟器转台系统性能指标,优化目标函数,并得到PI 控制最优参数,控制系统指标很好被跟踪,具有一定鲁棒性[9]。Angel Ruiz将史密斯预估器和结构对称的 send-on-delta(SSOD)采样方案相结合,优化了PI控制器,不确定因素下控制系统仍能跟踪控制系统指标且具有强的稳定性[10]。
考虑难以建立准确数学模型的控制系统,但也要实现精确控制,同时达到控制性能,基于现代控制理论方法,如基于干扰观测器的控制器设计、鲁棒控制器设计、自适应控制、神经网络控制、自抗扰控制、模糊控制、滑模变结构控制方法等提出[11]。
S.Komada,K.Ohnishi 等人首先提出干扰观测器理论,在控制器自身参数发生变化以及控制系统受到外部力矩干扰时,真实被控对象输入和被控对象的名义模型输出之间会产生差值,定义差值为等效干扰[12],设计干扰观测器来等效估计实际干扰。基于干扰观测器的控制器设计过程中时,可分别设计扰动观测与补偿部分和跟踪控制部分。Joo Y通过将扰动的内部模型补充到干扰观测器结构中,设计干扰观测器,在模型不确定参数属于任意大的有界集合,该干扰观测器也能观测出控制系统内部扰动,保证系统较强鲁棒性以及抗干扰能力[13]。
鲁棒控制算法提出于20世纪50年代,理论方法有 H∞控制理论、结构奇异值理论、Kharitonov 区间理论[14]。当被控对象因其不确定性而对模型参数变化不敏感时,设计控制器来满足控制系统的高稳定性与高精度。J.Yao提出一种基于扩张观测器的自适应鲁棒控制器,该控制器能够消除不确定因素对直流电机控制效果的影响,控制器所具有的全局鲁棒性保证了控制系统稳定性和不确定条件下的高精度跟踪能力[15]。王建宏设计了基于 H∞的内模控制方法,实验验证该方法能够提高系统高阶动态性能和抗干扰能力[16]。
自适应控制是在没有精确被控对象数学模型条件下,分析输入输出,增加自适应回路来调节控制器参数,来实现控制系统精确控制。1998 年,JE Seem 提出用于改变闭环中PI控制器增益的自适应控制算法,实验结果验证其计算效率高[17]。Tomei P提出六阶非线性自适应控制算法,解决了在负载转矩恒定未知条件下的无传感器永磁同步电机跟踪控制[18]。王卫红提出基于模型参考自适应复合控制方法,解决飞行模拟器转台中存在不确定因素,自适应调整增益同时引入数字前馈控制来提高系统控制精度[19]。张德成通过自适应控制算法实现补偿高性能伺服转台扰动力矩[20]。
神经网络控制方法是智能控制算法之一,学习能力强大、逼近连续非线性函数优点,解决系统中存在高度非线性控制问题,隐含层神经元激活函数具有非线性映射功能,可逼近任意非线性函数,为解决非线性控制问题提供方法。Abbas,Hamou Ait提出基于神经网络的系统反馈线性化控制,减小系统统动力学与数学模型误差,降低系统跟踪误差[21]。电机负载扰动呈非线性特性,梅从立将神经网络引入到所建立感应电机模型中,设计神经网络直接逆控制器,达到对感应电机调速系统的在线学习与控制[22]。
在自抗扰控制方面,李杰设计线性/非线性自抗扰控制切换控制,达到了系统的高抗扰能力、高精度要求[23]。Guo B Z验证自抗扰控制器在不确定模型和外部扰动条件下的多输入多输出控制系统收敛性,实验验证自抗扰控制能够使系统在不确定扰动条件下实现指标精确跟踪[23]。
在模糊控制方面,路平结合模糊控制和 PID 控制对飞行模拟器转台进行MATLAB仿真实验,仿真验证其具有良好的动态性能[24]。纪志成结合模糊控制和自适应,基于转台数学模型,实现无刷直流电机的自适应模糊控制[25]。吴燕燕在转台控制中引入模糊控制,精确控制转台系统。对比传统 PID 算法,证明该算法精确性和鲁棒性[26]。
在滑模控制方面,刘金琨研究飞行模拟转台不确定伺服系统,设计新型滑模控制策略,仿真验证了该算法具有优良控制性能[27]。反步滑模控制策略对不确定性匹配条件和飞行模拟转台伺服系统的外部扰动具有很强的鲁棒性,继承了反步控制对具有失配不确定性的不确定非线性系统具有良好瞬态质量的特点。反步滑模控制可以有效解决伺服系统中的参数扰动和非线性摩擦补偿问[28]。
三步法控制是一种首先应用在解决汽车跟踪控制问题的控制测略。系统在实际控制过程中,不确定扰动变化使得系统模型输出存在偏差,但系统控制过程又存在滞后特性。系统被控量发生变化之前,反馈控制量不能马上对系统进行调节,降低系统调节效果。提高控制系统的控制效果,学者设计前馈加反馈的复合控制方法。在不确定扰动影响系统指标之前,给系统中加入补偿控制。同时,前馈控制能够将系统工作点调节到平衡点附近,使得反馈控制仅仅在工作点附近的小范围内工作[29]。本文将三步法控制器扩展到飞行模拟转台伺服系统,并且证明了可以渐近收敛到期望轨迹。在飞行模拟转台伺服系统上进行了仿真实验验证设计的轨迹跟踪控制器的有效性。
1 系统结构及原理
飞行模拟转台伺服系统动力学:
考虑非线性摩擦的飞行模拟转台伺服系统结构如图1所示,表达式如式(1)[30]。

图1 飞行模拟转台伺服系统结构框图
根据伺服系统的上述结构,其控制系统动态方程可以描述为:
(1)
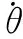
当考虑飞行仿真转台伺服系统参数摄动和电机力矩波动等不确定因素时,公式(1)可转换为:
(2)

通过以上分析,飞行模拟转台伺服系统可表示为以下形式[10]:
(3)

通过以上分析,飞行模拟转台伺服系统可表示为以下形式[31]:
(3)

摩擦力存在于日常生活运动中。接触面积大小、接触物体粗糙程度以及物体接触时的相对速度等都会影响摩擦力大小。互相接触的两物体,在相对静止条件下,此时两者之间的力为静摩擦力。对其中一物体施加外力后,两者的状态变为相对运动。在此过程中,两物体间摩擦力经历4个不同阶段变化。学者研究发现,运动速度影响摩擦力大小,4个不同阶段变化如下。
1)接触面发生弹性形变:两相互接触的物体在相对静止状态发生变化间隙,两接触面间始终为“粘着”状态,但两接触面之间存在微弱且难以观察的运动。但此时静摩擦力抑制两接触物体间出现相对运动,施加在物体上面外力大小决定着静摩擦力的大小。可当外力达到某上限时,物体状态到达第二阶段,静摩擦在此时达到最大值。
2)边界润滑:两接触物体在发生相对运动时候,因速度低,接触面材料成影响两接触物体间摩擦力大小的主要因素。
3)部分润滑:当外界施加力持续变大,那么两物体之间接触面不处于完全接触阶段,摩擦力会逐渐变小。
4)全液体润滑:物体速度逐渐变大,两物体间接触面完全分离开,接触面不影响摩擦力大小,此时摩擦力大小由粘性摩擦力矩决定。粘性摩擦力矩和物体运动速度成比例关系。摩擦力速度越快则摩擦力就越大[32]。
控制系统不同,其机械特性也会出现大的差异,不同控制系统间表现出摩擦特性不同。分析不同的控制系统,则要研究摩擦扰动的影响因素有,描述合适模型的摩擦力。本文对飞行模拟转台位置进行控制,所接触的摩擦面较多,转台组成部分之间接触面光滑程度不同。
本文采用LuGre摩擦模型模拟非线性摩擦补偿[33]。其数学模型为:
(4)
其中:
(5)

2 飞行模拟转台伺服系统控制设计
2.1 微分观测器设计
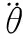
(6)


(7)

(8)
2.2 非线性控制器设计
第1步:类稳态控制
(9)
此步骤控制算法与当前测量或者估计状态相关,而不依赖系统真实的稳态,所以称为类稳态制。
第2步:变参考前馈控制

(10)
进而得:
(11)
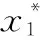
第3步:误差反馈控制
从前两部假设条件可得出,类稳态控制us与参考前馈控制uf一起作用的条件下,飞行模拟转台伺服控制系统的位置转角输出不能保证达到期望值。为了使得飞行模拟转台伺服控制系统实际位置转角轨迹跟踪期望值轨迹,在以上两步骤的基础条件下添加误差反馈控制ue,最终得到飞行模拟转台伺服控制系统控制律为u=us+uf+ue。
(12)

(13)
对该李雅普诺夫函数求导:
(14)

(15)


(16)

(17)
定义一个李雅普洛夫函数:
(18)
对该李雅普诺夫函数求导:
(19)
(20)

21
得到最终误差反馈控制律为:
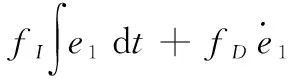
(22)

2.3 稳定性与鲁棒性分析
由于飞行模拟转台伺服系统存在未建模动态、参数不确定性和外界扰动。将控制律(22)代入式(3)中,经过整理可以得到闭环误差系统动态:
(23)
取李雅普洛夫函数:
(24)
对该李雅普诺夫函数求导:
(25)
(26)

3 仿真结果及分析
飞行模拟器转台伺服控制系统中存在参数不确定性以及非线性摩擦干扰,本文中设定系统期望转角输出为正弦信号。飞行模拟器转台伺服控制系统的主要参数和标称值如下:
其中,PWM功率放大器放大系数Ku=11。电枢电R=7.77 Ω。电机转矩系数Km=6 Nm/A。转动惯量J=0.6 kgm2,电压反馈系数Ce=1.2 V/(rad/s)。
位置转角期望输出值为正弦函数,模型参数设定偏离值为20%,设计的微分观测器参数值为λ0.1=80,λ0.2=120,λ1.1=200,λ1.2=12.5,terminal吸引因子参数为l1=5,l2=7。图2为复合不确定扰动F仿真曲线图。分析图2,本文设计的观测器能够观测系统的复合不确定扰动,观测误差小于实际值的2%。

图2 复合不确定扰动F仿真曲线图
在观测出系统复合不确定扰动基础上设计非线性控制器,非线性控制器的调节参数为k0=10,k1=18,k2=42。图3为位置转角仿真曲线图。图4是位置转角跟踪误差仿真曲线图。分析图3和图4,非线性控制器与PID控制器作用相互比较,分析出非线性控制器在系统参数不确定等扰动条件下,能够快速稳定跟踪期望的位置转角轨迹,跟踪误差小于0.01 rad,验证其具有鲁棒性。

图3 输出转角仿真曲线图

图4 输出转角跟踪误差仿真曲线图
4 结束语
飞行模拟转台伺服系统在实际跟踪控制过程中存在参数不确定性、非线性摩擦等不确定性问题。文章提出了一种基于微分观测器的飞行模拟转台伺服系统非线性控制方法。考虑控制过程中存在不确定性问题,难以直接测量得到,设计了微分观测器来估计复合不确定扰动。设计非线性控制器来控制飞行模拟转台伺服系统,使得系统可以收敛到期望位置转角信号,并分析控制器作用条件下系统的鲁棒性。利用MATLAB/Simulink仿真试验平台验证了文中提出的控制策略能够使系统有效跟踪期望位置转角,具有一定工程应用价值。

