基于Snake-Net算法的刺绣针法识别
王敬雪 庄梅玲

摘 要:为有效提取刺绣图像中针法的特征值,实现刺绣针法的分类识别,在分析刺绣针法特点的基础上,提出了点状针法、线状针法和块面状针法的三大针法分类,并以占主体的块面状针法中的齐针、抢针和套针3种基础针法为处理对象,分析对比其针法特征,构建针法模型。针对刺绣针法图像进行图像纹理细节的增强处理,基于Harris 角点检测特征点和Canny轮廓筛选,对传统Snake算法进行改进,形成智能化HC-Snake模型,实现对目标轮廓的智能化识别并提取目标图像的纹理及颜色特征。通过数据的方差分析确定CONsd,IDMsd,Ea,Esd,ENTa,ENTsd,CORsd,SM和TM共9个特征指标,建立特征数据集。最后,建立神经网络分类模型,对针法样本进行分类,并对识别模型进行了实例验证。结果表明,该模型可以实现刺绣针法图像的分类,且分类准确率达到93.3%。
关键词:刺绣针法,针法模型,HC-Snake模型,灰度共生矩阵,颜色矩,BP神经网络
中图分类号:TS941.2
文献标志码:A
文章编号:1009-265X(2023)04-0236-14
收稿日期:2022-09-21
网络出版日期:2023-02-21
基金项目:青岛大学研究项目(JXGG2019080)
作者简介:王敬雪(1997-),女,山东淄博人,硕士研究生,主要从事服饰数字化及感性评价方面的研究。
通信作者:庄梅玲,E-mail:zmlqdu@126.com
传统刺绣是中华民族的艺术瑰宝,刺绣针法则是刺绣的基础。近年来,随着国家对传统文化的弘扬和传承,对传统刺绣艺术的研究也越来越多。其中,多数研究集中于刺绣的风格特点、文化内涵、表现形式及新时代背景下的创新与应用等方面[1-3],针对刺绣针法的技艺和工艺特点的研究相对较少,已有的相关研究主要是结合针法特点和走线趋势,从理论上分析某种特殊针法[4-5]。在数字化智能化飞速发展的时代,运用数字化技术对传统艺术作品进行传承和保护的研究越来越受关注。近几年针对刺绣的研究主要是刺绣图案的智能化提取与分割[6]、风格迁移[7]和分类识别[8]等,以刺绣的整体风格为基础的图像识别研究。而针对刺绣针法技术和工藝细节的识别较少,仅杨蕾等[9]提出以导向滤波作为尺度变换函数的特征提取模型,将针法样本与已知针法模板进行特征匹配,识别针法类别。但其研究处理的手绣样本形状相似,图像清晰度较高,样本纹理特征可控,与网络中形态各异、噪声众多的刺绣图像相比,方法适用性不足,并且该研究更着重于算法的理论创新。基于目前的研究现状,本文拟形成一种适应性更广的刺绣针法识别模型,通过分析刺绣针法的技术及工艺特点,对网络中获取的普通刺绣图像,进行针法多特征分析,运用智能算法进行归类,形成一种更为通用的智能化刺绣针法识别分类模型。
从网络中获取的刺绣图像,需进行目标分割,获得目标样本,以提取特征。近年来图像分割算法丰富,边缘检测和色彩聚类算法都应用广泛,其中Canny[10]和K-means[11]更是凸显。K-means根据图像色彩,分割出不同颜色聚类的图像,效果良好。但刺绣图像的色彩多混合掺杂,目标与干扰项无固定的色彩或色差,色彩聚类不适用。Canny算子检测的边缘相对清晰,特别是灰度图像,但受参数设定的影响,会出现轮廓检测不完整或者过度检测等问题。因此本文将其用于初始轮廓的界定,结合活动轮廓模型Snake算法[12-13],互相优化,以获取更加圆顺、完整而准确的目标轮廓。最后,神经网络是效果优良、应用广泛的分类识别算法[14-16],因此本文选择BP神经网络来建立针法分类识别模型。
1 刺绣针法分析及结构模型构建
针法和丝线是刺绣的主要构成因子,共同塑造
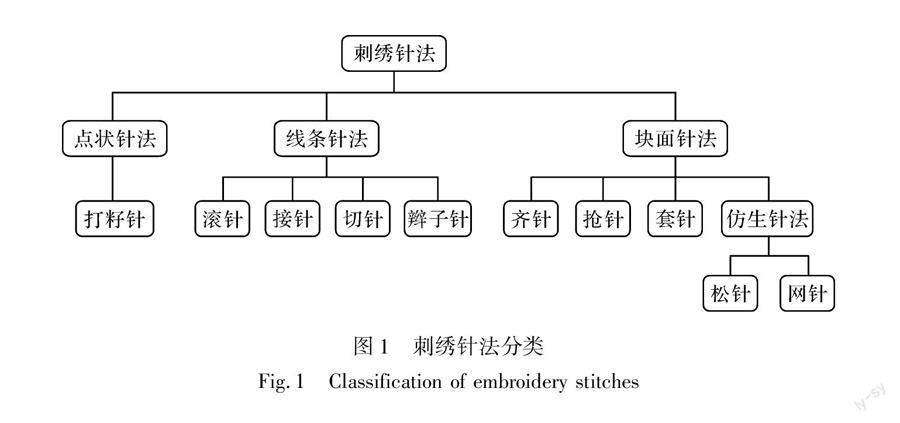
刺绣的艺术风格。从平面构成的角度,刺绣的针法可分为点、线、面3类[17],本文结合针法的技术工艺特点分析,将刺绣针法定义为点状针法,线条针法和块面针法3类,分类图归结如图1。
点状针法和线状针法主要表现为形成刺绣中的独立点和线条,如制作花蕊的打籽针以及形成纤细枝条或勾勒轮廓的滚针、切针等。点、线状针法在刺绣图案中呈点缀状分布,作品整体以块面针法为主,所以本研究以块面针法为研究重点。
1.1 针法特征分析
块面针法非常丰富,其中,基础的针法有齐针,抢针和套针,都具有针脚排列紧密,绣面匀称平整的特点。下面对3种基础块面针法的基本特点进行分析和对比。
a)齐针(Flush stitches)
齐针,线条均匀、齐整,平行排列构成单色块面,起针和落针都紧靠纹样边缘,针脚紧密,块面间无重叠,不露底,模型归结为图2(a)。从彩色图片(图2(b))和灰度图像(图2(c))中可见,纹理一致,灰度均匀。以同色系渐变为主,色彩跨度小。
b)抢针(Grabbing stitches)
抢针,密度相同,长短均匀的短齐针分层刺绣,构成多层块面,每一批抢针头尾相接而互不交错,在模型上归结为图3(a)。颜色区2的起针和颜色区1的落针在同一线条上,颜色变化明显,颜色区域间形成明显的分界线,在抢针的灰度图像(图3(c))中,可见明显的分块,色彩的跨度较大。
c)套针(Overlapping stitches)
套针,长短不一的线条相互穿插,分层绣制,层层相套,不露针脚,模型可归结为图4(a)。颜色区1的落针和颜色区2的起针交叉混合,批线相互穿套,密度相对不均匀,且内部边缘在灰度图像及二值图像中表现为折线状;同时,线条穿插导致颜色混合,颜色变化虽然明显,但过渡自然,有晕色渲染的效果。在彩色图像(图4(b))中,呈现渐变效果,而在灰度图像(图4(c))中,呈现为灰度均匀变化,但色彩跨度较大。
经过以上的分析,对3种针法的特征进行对比分析如表1。
比较发现,3种针法在形状上不呈现特征的聚类及类型间的差别,区别明显的特征为纹理特征和颜色特征。纹理特征上:齐针呈现整体规则化排列;抢针呈现分批型排列,各批内纹理整齐排列,批间有显著差异;套针最为曲折、复杂,存在批线间相互穿插。颜色特征上:主要表现为灰度变化,齐针颜色单一,灰度均匀;抢针和套针色彩丰富,抢针灰度变化明显,有分块,套针灰度均匀变化,呈渐变,差异明显。以上对不同特征的分析,为接下来的图像识别处理奠定基础。
2 块面针法的目标分割
通过块面针法的准确识别可以对刺绣的种类、特点及蕴含的寓意进行有效分析,所以本文将以块面针法为对象,分析其包含的3种针法特点及规律,运用图像处理工具,设计智能算法对块面针法进行智能识别。算法流程图如图5所示。
2.1 预处理
通过分析比较,发现3种基础块面针法的区别主要体现在纹理细节部分。首先对清晰度较差的网
络图片进行预处理,一方面增强对比度,突出目标边缘,便于实现目标分割,另一方面增强纹理细节,便于提取纹理特征。本文的图像预处理步骤为:
2.1.1 增强对比度
a)利用式(1)将彩色图像(图6(a))灰度化(图6(b)):
Y=0.299R+0.587G+0.114B(1)
式中:Y为灰度图像,R,G,B分别为彩色图像的红、绿、蓝三个分量。
b)利用stretchlim函数计算灰度图像自适应变换的最佳阈值。
c)利用调整对比度函数imadjust,调整灰度范围。
d)输出增强的灰度图像(图6(c))。
2.1.2 增强纹理
a)数据类型转换,由uint8转为double(图6(d))。
b)选择3×3的拉普拉斯模板w=[0,1,0;1,-4,1;0,1,0],进行滤波处理。
c)提取图像中的边界及纹理等细节,输出细节图像(图6(e))。
d)将双精度灰度图像与细节图像作差,增大纹理细节与相邻像素的灰度差,得到纹理增强图像(图6(f))。
算法处理流程及结果见图6。
通过上述处理发现:对比度增强和纹理增强后的图6(c)、图6(f),都比处理前的图6(b)的边缘和纹理更加清晰,为下一步的目标提取做好准备。
2.2 基于改进Snake算法的交互式目标分割
目标分割是将图像中的特征区域从复杂背景中分离出来的技术和过程。本文基于对大量目标样本的处理,获得齐针、抢针和套针样本的特征信息,建立针法智能识别模型。所以获取刺绣图像后,首先对图像中的不同针法区域进行目标分割,获得齐针、抢针和套针的目标样本,为下一步提取特征信息做好准备。
本文研究的刺绣图像,其形状特征丰富,单一的图像分割算法像阈值法、边缘检测法等,难以实现对刺绣图像包含的各种针法区域的精确分割。而活动轮廓模型Snake算法利用图像的高层信息,将图像分割问题转化成数学上求能量泛函的问题,对图像轮廓进行求解[18],在内力、外力的共同约束下,从初始轮廓向真实轮廓逼近,识别的目标轮廓以数学曲线的形式呈现,比较连续、光滑,具有良好的匹配效果和形状检测能力。并且该算法是一种交互式目标识别算法,通过智能人机交互在预选样本时加入经验的关键点设置,识别的轮廓跟随控制点移动,对比单一的图像分割算法可以更好地从包含多种针法区域的刺绣图案中预先选择各目标区域,实现更精确的目标分割。
传统的Snake算法中,控制点是人为选择的,虽然比较灵活,但受经验等主观因素的影响较大,而且手动选点时,无法精确选取同一控制点,导致每次试验结果存在差异;人工选点智能化程度较低,不符合当前智能化发展的趋势。
基于对Snake算法的优缺点分析,本研究着重对其人工选取控制点的误差性和智能化程度不高的问题,改进控制点的选取算法,提出一种更加客观且智能化的改进Snake算法。
2.2.1 改进Snake算法——HC-Snake算法设计
本研究的改进Snake算法——HC-Snake(Harris and Canny-Snake)模型,首先基于Harris角点检测[19-20]获取角点,然后基于Canny算子确定初始目标轮廓[21],初始轮廓筛选角点作为Snake算法的控制点集,替代传统Snake算法的人工选点,最后进行轮廓识别。算法设计步骤如下:
a)获取目标图像的特征角点集
计算初始图像a的x轴和y轴方向的梯度Ix,Iy及其平方;高斯滤波平滑处理;构造自相关矩阵M,計算角点响应度R(见式(2)-式(5)),设定R的阈值,并判断该点是否为角点。遍历图像,获得角点集合H[20]。
Eu,v(x,y)=∑u,vwu,vIx+u,y+v-I(x,y)2 (2)
式中:Eu,v为窗口灰度值,u,v分别表示以像素为中心的窗口在x轴和y轴的偏移量,(x,y)是窗口内所对应的像素坐标位置,wu,v为二维高斯窗口函数,wu,v=exp-u2+v22σ2。将 Eu,v(x,y)化为二次型可得:
Eu,v(x,y)=(u,v)Muv(3)
M=∑u,vwu,vI2xIxIyIxIyI2y(4)
R=det(M)-k(tr(M))2=λ1λ2-k(λ1+λ2)2(5)
式中:λ1、λ2为M矩阵的特征值,det(M)是矩阵M的行列式,tr(M)是矩阵M的迹,k∈[0.04,0.06]。
b)获取目标图像的初步外轮廓
基于Canny算子计算图像初始边缘。输入初始图像a,灰度化处理得灰度图像A,进行高斯平滑。计算相邻像素点的灰度变化,梯度较大的位置,作为边缘点,处理得到初始边缘的二值图像。取初始边缘上任意一点Ai作为种子,计算Ai的中心像素Pi。8-邻域内,若存在Ai+1与Ai邻接,且Pi+1≈Pi,将Ai+1存入集合A1,并作为下一次生长的种子点;若8-邻域内无相似像素点,停止运算。遍历集合A1,取A1中像素值为1的点,形成初始轮廓点集Ai{Ai, i=1,2,…n}。
c)确定Snake轮廓控制点集
Snake算法获取的轮廓受轮廓控制点位置影响,控制点越接近真实轮廓,收缩效果越好。对于轮廓点集合A和角点集合H,H中的点与A中的点距离越近,越接近真实轮廓,为了最大程度的选到离目标最近的角点,设计n×n模板覆盖算法筛选角点。覆盖算法如图7所示:其中A(i,j)为模板中心点,属于Canny轮廓点,以5×5的模板为例,角点a、c、d被该模板覆盖,可以作为Snake控制点,角点b、e未被覆盖,舍弃。通过覆盖算法获得包含m个控制点的集合C,并按照顺时针排序。
将控制点集C的首点C1(s)和末点Cn+1(s)位置進行重合,形成闭环集。
C(s)=[x(s),y(s)], s∈[0,1](6)
d)进行轮廓插值。
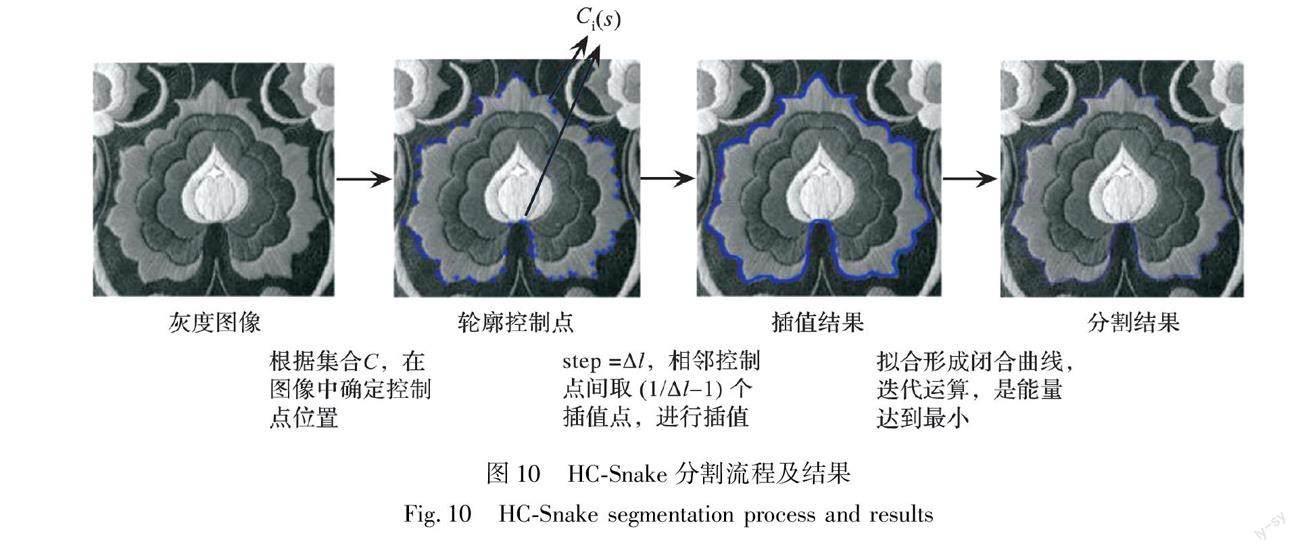
根据点集C(s),用三次方样条数据插值算法,步长step=Δl,在[1,n+1]内取点,任意相邻两控制点Ci(s),Ci+1(s)间插入(1/Δl-1)个插值点,使插值点均匀分布。对所有的控制点都完成插值,顺次连接拟合得到光滑的闭环曲线L。
e)计算内部能量值
Snake模型的内部能量(EIn)是曲线弯曲收缩所产生的能量,包括弹性能量(EEl)和弯曲能量(EB)。在活动轮廓形变过程中,EEl使曲线收缩,EB使轮廓线保持光滑度和连续性,公式如下[12]:
EIn=EEl+EB=α(s)dCds2+β(s)d2Cds22(7)
式中:α(s)和β(s)分别影响着Snake模型的弹性和刚度。α(s) 对轮廓L的影响更大,值越大,轮廓线越平滑;β(s)对轮廓L的影响相对较小,实际处理中,默认为0。
由于α(s)过大难以准确分割尖角及凹陷区域,过小易受噪点影响,因此,本算法对比了α(s)=0.005,0.01,0.02,0.05,0.1的分割效果,发现α(s)=0.01时,分割效果最好,结合实验效果,设置α(s)=0.01。
f)计算外部能量值
Snake模型的外部能量主要是从图像中获得的图像力EIm,由3个部分构成,计算如式(8):
EIm=wl*El+we*Ee+wt*Et(8)
式中:El、Ee和Et的加权和决定了Snake轮廓线是否趋向于线条(lines)、边界(edges)和终端(terminations),wl、we和wt分别为El、Ee和Et的权值。
El=f(x,y)(9)
Ee=-SymbolQC@f(x,y)2(10)
式中:El是基于轮廓线的能量,f(x,y)是图像在(x,y)处的灰度,wl的符号决定了Snake形变时偏向亮线或暗线; Ee使Snake轮廓线趋向于图像的强边缘;wt*Et则反映了轮廓线的端点或角点对轮廓线可能产生的影响。图像f平滑得到光滑图像g,其沿曲线的梯度方向为φ(x,y),平行和垂直的梯度方向分别为:
n(x,y)=(cos(φ(x,y)),sin(φ(x,y)))n⊥(x,y)=(sin(φ(x,y)),cos(φ(x,y)))
据此,可以获得平滑图像上灰度不变的轮廓的曲率:
Et=φn⊥=2g/n⊥2g/n
=(2g/y2)(g/x)2-2(2g/xy)(g/x)(g/y)+(2g/x2)(g/y)2((g/x)2+(g/y)2)3/2(11)
g)计算总的能量
Etotal=∫10(EIn+Eim)(12)
根据图像的梯度,计算并对比每次循环的内部和外部能量,直到获得最小能量MIN(Etotal)时,停止迭代。
h)输出分割完成的图像。
2.2.2 算法仿真与结果分析讨论
对刺绣图像a应用上述算法处理如下:
a)确定Snake控制点(图(8))
b)覆盖模板尺寸确定
为验证距离对控制点选取的影响,分别以3×3,5×5,7×7的模板进行实验,提取H中的控制点,结果如图9所示。
对比图9的结果,发现3×3的模板较小,部分特征明显的角点并未被覆盖,控制点选取不全面;7×7的模板较大,选中较多干扰点;5×5的模板确定的控制点相对全面,且干扰较少,因此,选用5×5的模板作为确定控制点的通用模板。
c)HC-Snake算法分割流程(图10)。
d)结果分析与讨论
将本文算法与Canny算法提取的边缘作比较,发现:Canny算子获取的轮廓虽贴近目标轮廓,但存在干扰边缘或缺口,并呈锯齿状,见图11(a)。由于Canny算法通过计算图像梯度提取边缘,在计算中,纹理清晰且与边缘相接的位置,也会被标记为边缘,边缘两侧像素梯度小,则会出现断口。并且,Canny算子是像素级别的,边缘易呈现锯齿状,不顺滑。而本文的HC-Snake算法检测结果更好地克服了这些问题。
2.2.3 算法应用
将本研究的HC-Snake算法用于传统刺绣针法的轮廓识别,依次进行齐针、抢针、套针的区域分割,得到对应的分割区域,分割结果见图12。
从图12中可以发现,基于HC-Snake模型的分割算法实现了目标区域的精确分割,由于可以预设轮廓点,所以无论是外表形态比较规整的,还是边缘有明显凸凹的的目标,都能实现目标区域的精确分割。通过该目标分割算法,对多幅刺绣图像进行目标分割,获得了多幅齐针、抢针和套针样本。
3 目标图像特征的选取
通过前两部分的研究,获得了多幅齐针、抢针和套针的样本,并选择能有效反映纹理和颜色特征变化的数学模型灰度共生矩阵和颜色矩,提取纹理特征和颜色特征。
3.1 纹理特征分析
灰度共生矩阵(Gray level co-occurrence matrix,GLCM)[22]是用统计方法,通过对图像中包含的灰度信息出现的频次进行计算,反映图像方向、相邻间隔、变化幅度及快慢上的综合信息。
纹理方面通常通过分析图像灰度共生矩阵的对比度、同质性、能量、熵、相关性5个指标,对图像的纹理进行描述和分析[23-24]。任意两个像素,灰度级为a,b,该像素对(a,b)在方向Φ上以距离d出现的频率为PΦ,da,b,本文中,d取默认值为1,Φ取0°,45°,90°和135°4个方向,计算取均值和标准差,避免误差,5个指标的计算公式如下:
对比度(Contrast,CON):反应图像的清晰度和纹理的沟纹深浅,对比度越大,纹理越清晰。
CON=∑a∑b(a-b)2PΦ(a,b)(13)
熵(Entropy,ENT):描述图像具有的信息量的度量,表明图像的复杂度,熵越大,图像纹理越复杂。
ENT=-∑a∑bPΦ(a,b)log2PΦ(a,b)(14)
能量(Energy,E):灰度共生矩阵各元素值的平方和,是图像纹理的灰度变化稳定程度的度量,反应了图像灰度分布均匀程度和纹理粗细度。
E=∑a∑bP2Φ(a,b)(15)
同质性(Inverse Different Moment,IDM):度量图像纹理局部变化,值越大,图像纹理越均匀。
IDM=∑a∑bPΦ(a,b)1+a-b2(16)
相关性(Correlation,COR):度量图像的灰度级在行或列方向上的相似程度,值越大,相关性越大。
COR=∑a∑babPΦ(a,b)-μxμyxy(17)
其中,μx=∑aa∑bPΦ(a,b)μy=∑bb∑aPΦ(a,b),
x=∑a(a-μx)2∑bPΦ(a,b)y=∑b(b-μy)2∑aPΦ(a,b)。
研究分别选择了齐针、抢针和套针样本各30个,按照式(13)—式(17)分别计算其灰度共生矩阵的5个指标,获取5个指标的均值(Average)和标准差(Standard Deviation)作为纹理特征数据。
3.2 颜色特征分析
颜色矩[25]是由Stricker和Orengo提出的一种简单有效的颜色特征表示方法,无需对颜色空间量化,而且特征维度低,颜色特征主要集中在颜色矩的低阶矩[26]。其中,一阶矩计算色彩的均值,体现图像的明暗程度,根据针法理论分析,不同针法的色彩均值并没有标准化的区别,舍弃。本文主要分析各样本的二阶矩和三阶矩。
二阶颜色矩(Second Moment,SM):计算标准差,反映图像颜色的分布范围,二阶矩越大,颜色分布范围越广,颜色变化越大。
SM=1N∑Nj=1Pi,j-∑Nj=11NPi,j212(18)
三阶颜色矩(Third Moment,TM):样本色彩的方差,计算样本颜色分布的对称性。
TM=1N∑Nj=1Pi,j-∑Nj=11NPi,j313(19)
式中:N为图像像素个数,i为颜色模型分量,灰度图像仅一个颜色分量,默认i=1,Pi,j为颜色分量 i 像素为 j 的概率值。
对3.1中的30个样本按照式(18)-式(19)分别计算二阶和三阶颜色矩作为颜色特征数据。
3.3 基于方差分析的指标检验和选择
对上述提取的10个纹理特征和2个颜色特征,针法类别是否显著影响这12个指标是后续进行三大针法分类的前提,因此用方差分析来检验针法类别对12个特征指标的影响,选择影响显著的指标用于后续针法分类。
以12个特征指标和3个针法类别作变量,计算每组的F值。每一组变量的自由度n=2,得出临界值为3.40,比较F值和临界值,最后得出3种针法对特征值的影响效果差异,方差分析结果见表2。
结果表明:CONsd,IDMsd,Ea,Esd,ENTa,ENTsd,CORsd,SM和TM这9个指标对特征值影响显著,因此选择该9个指标作为下一步智能识别分类的指标。
4 基于神经网络的块面状针法识别
BP神经网络是目前应用最广泛的神经网络模型之一,该模型一般包含三层:输入层,隐含层和输出层。利用梯度下降法和误差反向传播解决多层神经网络的隐含层连接权值的学习问题,具有较高的准确率和速率[14-16],因此本研究选择BP神经网络来建立针法智能识别模型。
4.1 模型构建
构建平台选用MATLAB.2018a,利用MATLAB中的神经网络模式识别工具箱对刺绣针法进行分类识别,将选择的9个指标作为输入特征,输出层为齐针、抢针和套针的类别。模型的拓扑结构如图13所示。
a)网络层数
3层:1个输入层、1个隐含层、1个输出层。
b)输入层
设置9个输入神经元:分别是CONsd,IDMsd,Ea,Esd,ENTa,ENTsd,CORsd,SM和TM。依次对应的输入特征向量[X1,X2,…,X9]。
c)隐含层
通过式(20)确定隐含层神经元个数
k=a+b+c(20)
式中:k为隐含层神经元个数,a和b分别是输入层和输出层的神经元个数,c∈[1,10]是常数。最终确定:k=10。
d)輸出层
输出层输出数据为针法的类别,是一维的数据,因此设置输出层节点数为1。
e)传递函数和训练函数
隐含层的传递函数选用tansig函数,输出层选用线性函数purelin函数。
f)训练方法
采用梯度下降训练法。按照式(21)调整输入层与隐含层之间的权值W1(s),按照式(22)调整输出层和隐含层之间的权值W2(s),使网络的误差平方和最小。
W1(s+1)=W1(s)+ΔW1(s)(21)
W2(s+1)=W2(s)+ΔW2(s)(22)
式中:ΔW1(s)为隐含层与输入层间的权值调整量,ΔW2(s)为输出层和隐含层间的权值调整量,s是迭代次数。
g)参数设置
最大训练次数:net.trainParam.epochs=1000;
学习系数:net.trainParam.lr=0.1;
目标误差的设置:
不同的目标误差设置,会影响训练的准确率,为获得更好的实验结果,测试了7个目标误差的训练结果。结果见表3。
结果表明:σt=0.0001和σt=0.0002时,准确率最高,ρ=83.33,但σt=0.0001对应的σv=0.3088,验证误差更小,因此设置net.trainParam.goal=0.0001。
4.2 模型训练及结果分析
按照上述设定参数,对3个类别的90个样本进行实验。
4.2.1 实验步骤
首先,将数据集90个样本随机分为训练集和测试集,分别占总数据集的66.67%和33.33%,以减少过拟合。
其次,数据归一化处理,减小数据数量级不同对神经网络训练效果产生的影响。输入模型进行训练。
再次,对输出结果设置分类阈值。
实验输出结果为Y=1,2,3,分别对应齐针、抢针和套针。由于对测试集的预测值是浮点数,因此设置分类的阈值:
If output<1.5,then Y=1;
If 1.5≤output<2.5,then Y=2;
If output≥2.5,then Y=3.
最后,繪制预测类别和实际类别的分类图。
4.2.2 结果与分析
a)实验准确率分析
经过训练,得出30个测试样本的预测结果和实际类别如图14所示,“*”为样本实际类别标签,“o”为预测结果类别标签。
由图(14)可见,“*”和“o”的重合度比较高,即预测结果与实际类别相符率较高。经过计算,该模型的预测准确率可达ρ=93.3%。
神经网络的训练中,各均方误差(mse,简称误差)的变化曲线如图15所示。训练集在迭代次数为s=15时,实际误差达到预期σt=0.0001。为了防止过拟合,产生验证集对每次训练集训练形成的神经网络的准确率ρ进行验证及测试,并根据验证集的准确率来决定是否停止训练。在迭代次数为s≥6时,验证误差σv反而逐渐增大。因此,在迭代次数s=6时,σv=0.14113,校验结果最好。
b)训练过程分析
在训练过程中,每一次迭代的数据变化如图16所示。由图16可见该模型在训练过程中梯度不断下降,准确率逐渐提高,在迭代次数为s=15次时,梯度为0.0031814,目标误差σt=10-6。验证失败(Val fail)表示验证集与训练集的梯度方向连续相反的次数,迭代次数s≥6时,验证集与训练集的梯度持续相反,直到s=15,达到目标误差,训练停止。
c)模型可靠度分析
为评估该模型的可靠程度,研究提取测试数据样本构建混淆矩阵见图17,横纵坐标分别是预测标签和实际标签,表格内的数值表示每类样本被分到每类标签的数量,其中,对角线上的是分类正确的样本个数,可以清晰明确的辨别样本预测是否被混淆,并且更充分的分析模型的可靠度[14]。
基于混淆矩阵,计算每类样本的精准率(Precision,P)、召回率(Recall,Re)以及精准率和召回率的调和平均数F1,计算公式如下:
精准率: P=TP/(TP+FP)(23)
召回率: Re=TP/(TP+FN)(24)
调和平均数: F1=2PReP+Re(25)
其中各参数含义如表4,计算结果见表5。
由表5可见:模型的精准率P>0.85,召回率R>0.9,类别1的精准率低于0.9,原因可能是样本分布不均匀;F1∈[0,1],是使P和R同时达到最高时,取得平衡的值,F1值越接近1,分类模型越可靠,表中F1值均大于90%,认为本研究构建的模型可靠。
4.3 模型应用分析
将本研究的整套算法:从网络获取的普通图像→预处理→HC-Snake算法分割→特征提取→神经网络分
类识别进行实例验证。实验流程及结果如图18。
通过实验发现,本文算法能够有效的对一幅网络普通图片进行针法识别,识别出了齐针、抢针和套针的针法类别。研究对比已有文献[9]中的平均匹配准确率为88%的结果,本文是基于网络上的普通图片,进行大量样本的特征提取而进行的分类识别,并且识别效率达到了93.33%,准确率更高,适用性也更广泛。
5 结 论
针对目前对刺绣针法的研究主要停留在理论分析上而缺少智能化的分类识别的问题,本文对刺绣针法特点进行分析对比,提出点状针法、线条针法和块面状针法三大分类。并以块面针法(齐针、抢针、套针)为例,通过分析归纳不同针法的特征,建立了针法结构模型,确定了可用于分类的特征为纹理特征和颜色特征。设计了HC-Snake算法改进传统Snake算法手动选取控制点,不够智能化的问题,通过提取特征,创建数据集,最后训练用于针法分类的神经网络模型。目前,齐针、抢针、套针仔细的针法识别相关文献比较少,相较已有研究而言,本文是基于网络上的普通图片,采用HC-Snake目标分割后获得的90例样本,对其进行特征提取,通过方差分析确定CONsd,IDMsd,Ea,Esd,ENTa,ENTsd,CORsd,SM和TM共9个特征指标,最后运用BP神经网络建立模型进行的针法分类识别,识别效率达到了93.33%,准确率更高,适用性也更广泛。
参考文献:
[1]彭迪,夏添,贺景卫.桃源刺绣“魏犨擒貘”纹样艺术特征及文化内涵探析[J].丝绸,2021,58(3):76-83.
PENG Di, XIA Tian, HE Jingwei. Analysis on artistic characteristics and cultural connotation of "Wei Chou captures a tapir" pattern in Taoyuan embroidery[J]. Journal of Silk, 2021, 58(3): 76-83.
[2]雒彬钰,闫亦农.科尔沁地区蒙古族刺绣纹样的特征分析及设计应用[J].染整技术,2021,43(12):42-54,64.
LUO Binyu, YAN Yinong. Analysis of the characteristics and design applications of Mongolian embroidery patterns in Horqin area[J]. Textile Dyeing and Finishing Journal, 2021, 43(12): 42-54, 64.
[3]陈栩,崔荣荣.福建畲族服饰刺绣工艺研究[J].丝绸,2018,55(5):78-83.
CHEN Xu,CUI Rongrong. Discussion on embroidery techniques of She minority in Fujian[J]. Journal of Silk, 2018, 55(5): 78-83.
[4]沈飞.京绣针法技艺研究[J].丝绸,2022,59(2):121-129.
SHEN Fei. A study on Beijing embroidery stitch techniques[J]. Journal of Silk, 2022, 59(2): 121-129.
[5]張竞琼,李頔.近代民间刺绣服装中正抢与平套针法比较[J].纺织学报,2012,33(5):106-110.
ZHANG Jingqiong, LI Di. Comparative study of encroaching satin stitch and parallel long and short stitch in modern folk embroidered costume[J]. Journal of Textile Research, 2012, 33(5): 106-110.
[6]王晓予,向军,潘如如,等.服饰刺绣图案的自动提取与色块分割[J].纺织学报,2017,38(9):120-126.
WANG Xiaoyu, XIANG Jun, PAN Ruru, et al. Automatic extraction on embroidered patterns of traditional costumes[J]. Journal of Textile Research, 2017, 38(9): 120-116.
[7]周杰,孙正兴,杨克微,等.乱针绣模拟的参数化生成方
法[J].计算机辅助设计与图形学学报,2014,26(3):436-444.
ZHOU Jie, SUN Zhengxing, YANG Kewei, et al. Parametric generation method for irregular needling embroidery rendering[J]. Journal of Computer-Aided Design & Computer Graphics, 2014, 26(3): 436-444.
[8]赵含笑.基于深度学习的刺绣图像分类与识别研究[D].西宁:青海师范大学,2020:6-50.
ZHAO Hanxiao. Classification and Recognition Algorithm of Embroidery Images Based on Deep Learning[D]. Xining: Qinghai Normal University, 2020: 6-50.
[9]杨蕾,胡慧,周军.刺绣针法图样特征点提取及匹配方法研究[J].计算机应用研究,2021,38(7):2231-2234,2240.
YANG Lei, HU Hui, ZHOU Jun. Study on feature points extraction and matching of stitch pattern[J]. Application Research of Computers, 2021, 38(07): 2231-2234, 2240.
[10]田贝乐,牛宏侠,刘义健.一种优化的Canny边缘检测算法[J].铁路计算机应用,2021,30(10):14-18.
TIAN Beile, NIU Hongxia, LIU Yijian. Optimized Canny edge detection algorithm[J]. Railway Computer Application, 2021, 30(10): 14-18.
[11]邢乐,张杰,梁惠娥,等.传统服饰云肩实物图像主色的智能检测[J].纺织学报,2017,38(11):110-115,123.
XING Le, ZHANG Jie, LIANG Hui'e, et al. Intelligent inspection of dominant colors for Chinese traditional folk Yunjian[J]. Journal of Textile Research, 2017, 38(11): 110-115, 123.
[12]龚雪慧.基于Snake的图像分割算法研究[J].电脑知识与技术,2014,10(13):3064-3066.
GONG Xuehui. Research on image segmentation algorithm based on Snake[J]. Computer Knowledge and Technology, 2014, 10(13): 3064-3066.
[13]吴鑫,李强,齐铂金.Snake模型和遗传算法在特殊焊缝提取中的应用[J].焊接学报,2018,39(9):83-89,132.
WU Xin, LI Qiang, QI Bojin. Application of snake model and genetic algorithm in special weld extraction[J]. Transactions of the China Welding Institution, 2018, 39(9): 83-89, 132.
[14]张加宏,孟辉,谢丽君,等.基于心冲击图和BP神经网络的心率异常分类研究[J].数据采集与处理,2021,36(3):565-576.
ZHANG Jiahong, MENG Hui, XIE Lijun, et al. Abnormal heart rate classification based on ballistocardiogram and BP neural network[J]. Journal of Data Acquisition and Processing, 2021, 36(3): 565-576.
[15]施端阳,林强,胡冰,等.基于改进BP神经网络的雷达剩余杂波抑制方法[J].兵器装备工程学报,2021,42(10):79-85.
SHI Duanyang, LIN Qiang, HU Bing. Radar residual clutter suppression method based on improved BP neural network[J]. Journal of Ordnance Equipment Engineering, 2021, 42(10): 79-85.
[16]罗火静,刘驰,徐步高.基于乳房形态特征的义乳曲面建模与体积预测[J].纺织高校基础科学学报,2020,33(4):71-77.
LUO Huojing, LIU Chi, XU Bugao. The surface modeling and volume prediction of breast prosthesis based on the breast morphological characteristics[J]. Basix Sciences Journal of Textile Universites, 2020,33(4):71-77.
[17]蔡子芬,叶洪光.浅析传统刺绣针法中“点线面”的表达[J].纺织科技进展,2021(2):10-12,32.
CAI Zifen, YE Hongguang. The expression of "point,line and surface" in traditional embroidery[J]. Progress in Textile Science & Technology, 2021(2): 10-12, 32.
[18]胡学刚,邱秀兰.基于Snake模型的图像分割新算法[J].计算机应用,2017,37(12):3523-3527.
HU Xuegang, QIU Xiulan. Novel image segmentation algorithm based on Snake model[J]. Journal of Computer Applications, 2017, 37(12): 3523-3527.
[19]姚依妮,王瑋.Harris角点检测算法的应用研究[J].智能计算机与应用,2022,12(8):148-151.
YAO Yini, WANG Wei. Application research on Harris corner detection algorithms[J]. Intelligent Computer and Applications, 2022, 12(8): 148-151.
[20]韩松奇,于微波,杨宏涛,等.改进Harris角点检测算法[J].长春工业大学学报,2018,39(5):470-474.
HAN Songqi, YU Weibo, YANG Hongtao, et al. An improved Harris corner detection algorithm[J]. Journal of Changchun University of Technology, 2018, 39(5): 470-474.
[21]李靖,王慧,闫科,等.改进Canny算法的图像边缘增强方法[J].测绘科学技术学报,2021,38(4):398-403.
LI Jing, WANG Hui, YAN Ke, et al. Improved Canny Algorithm for Image Edge Enhancement[J]. Journal of Geomatics Science and Technology, 2021, 38(4):398-403.
[22]桑卡,赫拉瓦卡,博伊尔.图像处理,分析与机器视觉[M].北京:清华大学出版社,2016:539-553
SONKA M, HLAVAC V, BOYLE R. Image Processing, Analysis, and Machine Vision[M]. Beijing: Tsinghua University Press, 2016: 539-553
[23]高士忠.基于灰度共生矩陣的织物纹理分析[J].计算机工程与设计,2008,29(16):4385-4388.
GAO Shizhong. Analysis of fabric texture based on GLCM[J]. Computer Engineering and Design, 2008, 29(16): 4385-4388.
[24]刘光宇,黄懿,曹禹,等.基于灰度共生矩阵的图像纹理特征提取研究[J].科技风,2021(12):61-64.
LIU Guangyu, HUANG Yi, CAO Yu, et al. Research on extraction of image texture Feature based on gray co-occur-rence matrix[J]. Technology Wind, 2021(12): 61-64.
[25]STRICKER M A, ORENGO M. Similarity of color images[C]//SPIE Proceedings, Storage and Retrieval for Image and Video Databases III. San Jose, CA. SPIE, 1995:2420.
[26]韩丁,武佩,张强,等.基于颜色矩的典型草原牧草特征提取与图像识别[J].农业工程学报,2016,32(23):168-175.
HAN Ding, WU Pei, ZHANG Qiang, et al. Feature extraction and image recognition of typical grassland forage based on color moment[J]. Transactions of the Chinese Society of Agricultural Engineering. 2016, 32(23): 168-175.
Embroidery stitch recognition based on Snake-Net algorithm
WANG Jingxue, ZHUANG Meiling
(College of Textile & Clothing, Qingdao University, Qingdao 266071, China)
Abstract:
The traditional embroidery is the intangible cultural heritage of the Chinese nation, and is vigorously promoted by the state. At present, most studies focus on the cultural heritage of embroidery and the application of embroidery in fashion products, while research for embroidery stitches is rarely found. In particular, the research on the recognition of embroidery stitches from the perspective of images is even less. Recognition for embroidery stitches is mostly done by experience, while few methods are available for intelligent recognition, which is not conducive to the digital protection of embroidery works.
In order to realize the intelligent recognition of embroidery stitches and promote the digital protection of embroidery, we firstly classify embroidery stitches as three classifications: point stitches, linear stitches and block stitches on the basis of analyzing the characteristics of embroidery stitches. Block stitches are the stitches whose proportion is the highest among the three classifications in the same embroidery works, while the flush stitches, the grabbing stitches and the overlapping stitches are three kinds of basic stitches which block stitches contain. With the three basic stitches as the processing objects, we analyze and compare the characteristics of these stitches, and construct the stitch model.
Secondly, the texture details of the embroidery stitch image are enhanced, and on this basis, the traditional Snake algorithm is improved. Based on Harris corner detection, corner points in the image are calculated to form a corner set. The Canny operator is used to detect the edge in the image, and the point set of the initial target contour is selected. Then, with the initial target contour as the center, the 5*5 template is used to cover the corner points, and the contour control points of Snake algorithm are determined, forming an intelligent HC-Snake model to realize the intelligent recognition of the target contour. The texture and color features of the target image including a total of 12 feature parameters such as the mean and standard deviation of contrast (CON), homogeneity (IDM), energy (E), entropy (ENT) and correlation (COR), the second-order color moments (SM) and third-order color moments (TM) are extracted by using the gray level co-occurrence matrix and color moments. Through the analysis of variance of the data, the significant degree of the influence of the stitch classification on each index is verified. It is found that the nine characteristic parameters including CONsd, IDMsd, Ea, Esd, ENTa, ENTsd, CORsd, SM and TM are significantly affected by the stitch classification, and they are identified as the characteristic indexes for classification, and a characteristic data set is established.
Finally, the BP neural network classification model is established, and the parameters of the neural network model are determined by comparative analysis, and the needle samples are classified and identified. With the help of confusion matrix, the accuracy and recall of the classification model are calculated to confirm the reliability of the model. In the meanwhile, the recognition model is verified by an example. The experimental results show that the model can realize the classification of embroidery stitch images, and the classification accuracy reaches 93.3%.
The HC-Snake algorithm proposed in this paper can effectively improve the shortcomings of the traditional Snake algorithm in manually selecting control points, and make it more intelligent. The establishment of embroidery stitch recognition models is used for stitch recognition of ordinary network embroidery images, which improves the accuracy and applicability of the recognition model. The research results can be used to promote the digital protection of traditional embroidery.
Keywords:
embroidery stitches; stitch model; HC-Snake model; gray level mo-occurrence matrix; color moments; BP neural network

