基于Dijkstra算法的北京景点旅游路径规划研究

叶小芹

（合肥城市学院机械与电气工程学院，安徽合肥 230000）

0 引言

北京作为中国的首都和历史古都，景点非常丰富，很多景点都具有特定的地质地貌、生态环境，尤其是悠久的历史、灿烂的文化吸引了很多游客，是中国的优秀旅游城市。每年去北京旅游的游客不计其数，以2022 年春节假期为例，北京景区累计接纳游客约758.3万人次，受新冠疫情影响，虽比2021年同比减少了2.9%，但比2020年增长3.6倍。面对如此巨大的游客数量，针对北京景点多、面积大、人流量大的特点，为了给游客更加舒适的体验，论文基于北京的几个著名景点，借助Dijkstra算法进行了旅游路线规划研究，能为智能旅游App的设计打下良好的基础。

1 Dijkstra算法介绍

在城市交通问题中，如果想找到城市A 和城市B之间一条中转次数最少的路线，即从顶点A 到顶点B所含的边的数目最少的路径，只需要从顶点A出发对该图进行广度优先搜索遍历[1]，一旦遇到顶点B 就可以停止，这是最简单的图的最短路径问题。但在很多情况下，还需要解决的问题是要找到城市之间的最短线路或者城市之间最节省的交通费用等问题，此时路径长度的度量就不再是路径上的数目，而是路径上的权值，即它所代表的相关信息，例如两个城市之间的距离或者途经所需的时间或者交通费用等，这类问题设计的都是最短路径问题。

例如从西安出发准备去北京、上海、兰州，该如何找到最佳的出行方案呢？也就是找到从西安出发到达三个目的城市的带权路径长度最短的那个路径方案。

最短路径问题一般分为两种情况：单源最短路径问题和每一对顶点之间的最短路径问题，常用的解决这两种问题的算法分别是迪杰斯特拉算法(Dijkstra)和弗洛伊德算法(Floyd)[2]，而解决旅游线路问题，主要是单源最短路径，主要应用Dijkstra算法。

2 Dijkstra算法思想

Dijkstra 算法是一种按照路径长度递增的次序，分别产生到各顶点最短路径的一种贪心算法，该算法把带权图中的所有顶点分成两个集合，S 和V-S，S 中存放已经找到最短路径的顶点，V-S中存放当前还没有找到最短路径的顶点[3]，算法将按照最短路径长度递增的顺序逐个将V-S 集合中元素加入S 集合中，直到所有的顶点都进入了S集合为止，其实这里用到一个很重要的定理，下一条最短路径或者弧即v0 到vi，或者中间经过S集合中的某个顶点，而后到达vi 的路径。这条定理可以用反证法来证明，假设下一条最短路径上有一个顶点vj是不在S集合中，即此路即为v0到vj再到vi，显然从v0到vj长度是小于v0到vj再到vi的长度，故下一条最短路径应该为v0 到vj，这就与题设的下一条最短路径v0到vj再到vi是相矛盾的，所以下一条最短路径上不可能有不在S 中的顶点vj，其中第一条最短路径是从源点v0 到各点路径长度集合中长度最短的那一条。

3 Dijkstra算法具体步骤

Dijkstra算法具体步骤如下：

第一步，对于网P=（V，E），将P 中的顶点分为两组，S和V-S，其中S为已求出的最短路径的终点集合，初始时仅包含S1，V-S代表尚未求出的最短路径的顶点集合，S 中各顶点之间的距离记为d，在顶点集合S中，如果存在弧＜S1,Si＞,则S1到Si之间的距离d＜S1,Si＞即其上的权值，否则记为无穷大[4]。

第二步，从V-S 中选取一个最小距离，将其关联的顶点K 加入S 中，且d＜S1,K＞为S1 到k的最短距离[5]。

第三步，以K作为新的基点，对S中各结点之间弧的权值进行调整，此时，如果源点S1 经过顶点K 到达顶点M 的距离小于S1 直达M 的距离，那么就调整顶点M的弧权值，即d＜S1,M＞=d＜S1,K＞+d＜K,M＞。

第四步，依次类推，反复执行以上第二步和第三步，直到集合S中容纳了全部顶点[6]。

以图1中的北京景点旅游线路图为例，运用Dijkstra 算法求得从天安门广场S1 出发到其余各顶点的最短路径，具体过程如表3所示。

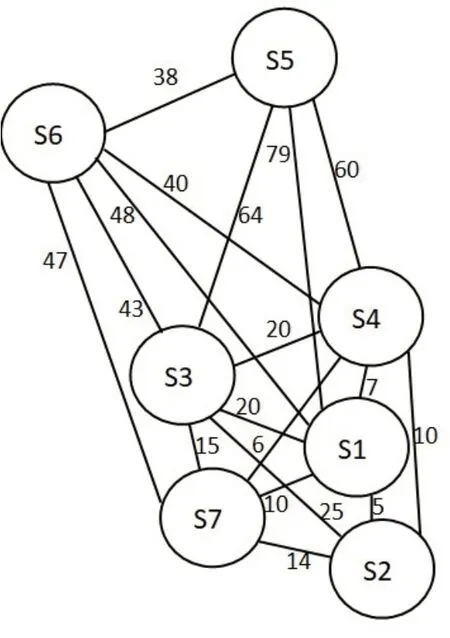
图1 北京部分景点旅游线路图

表3 Dijkstra算法应用实例

4 Dijkstra 算法在北京景点旅游线路规划中的应用

在基于Dijkstra 算法对旅游线路进行规划时，通常采用图形结构来表示北京景点中的实际路径结构，本文选取了北京的7个著名景点作为研究对象，这些景点的旅游线路图如图1所示，其中每个景点均用代码表示，具体代码对照表如表1所示。

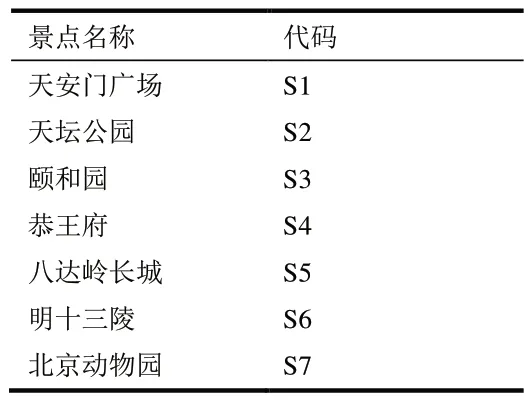
表1 北京部分景点代码

每个景点之间路线是互通的，各景点之间的距离信息如表2所示，以公里为单位。

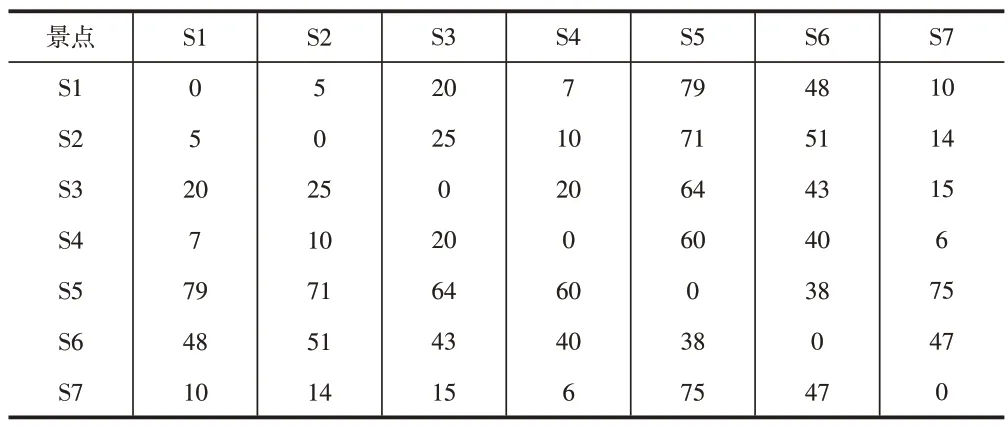
表2 北京部分景点的距离矩阵

为了更好地记录整个求解过程，设置表格来记录，列代表每一次的求解过程，即每一条最短路径的产生，行代表单源点到达目标点，矩阵中的元素值来代表单源点到达目标点的路径长度，为了更好地记录这个路径，同时记录了路径上的顶点，比如在这个无向网中，以S1作为出发点，如果采用邻接矩阵进行存储，那么扫描S1所在的行，就可以知道S1直接相邻的顶点有哪些[7]，可以看到，有S2到S7，路径长度分别为5、20、7、79、48、10，显然第一次可以选择的就是5这条最短路径，对应的目标点就是S2，即第一条最短路径是从出发点S1 到S2，路径长度为5，这条路径就是S1到S2的最短路径；接下来通过更新迭代来寻找第二条最短路径，根据刚刚介绍的基本思想，第二条最短路径要么来源于和S1直连的那些顶点，一条边，要么来自刚刚已经找到的从S1经过已求得的最短路径顶点S2，再到达目标点的两条边来组成，所以要来考查一下顶点S2,它可以邻接哪些顶点，扫描S2所在的行，除了S1，与S2 直连的顶点有顶点S3 到S7，其中S1 通过S2 中转到达S5 的路径长度是5+71=76，比S1 直达S5的路径长度短，所以要更新替换，替换路径为S1借助于S2 到S5，路径长度为76，其他的不变，第二条最短路径就是在20、7、76、48、10 这几个中进行选择，肯定选择7，所以找到第二条最短路径是从S1到S4,路径长度为7,这条路径就是S1 到S4 的最短路径；继续找第三条最短路径，它或者还是从源点到某一个目标点直达的，或者是从源点经过已求得的最短路径的顶点S4再到达某个目标点的，因此要来考查顶点S4，除去S1和S2，发现S4 直连出去的顶点有S3、S5、S6、S7，之前出发点S1 到S5 是经过S2 中转的，路径长度为76，现在经过S4 中转，路径长度只需要7+60=67，所以更新替换，另外之前出发点S1到S6是直达的48，现在经过S4 中转只需要7+40=47，所以也更新替换，此时可以选择的路径长度有20、67、47、10，所以选择10 这条，至此找到了第三条最短路径，从S1出发到S7，路径长度为10,这条路径就是S1到S7的最短路径；接下来找第四条最短路径，考查顶点S7，发现没有通过S7中转可以缩短路径的顶点，此时路径长度就在20、67、47中选择了，所以选择20这一条，即找到第4条最短路径，S1 到S3，路径长度为20，这条路径就是S1 到S3 的最短路径；接下来同理，第五条最短路径是S1经过S4中转，再到S6，路径长度47，最后一条，第六条最短路径是S1经过S4中转再到S5，路径长度是67，至此求得了出发点S1到其余6个顶点的带权最短路径长度了。

5 Dijkstra算法改进

在对北京景点的路线进行规划而设计出最短路径时，结合北京部分景点的旅游线路图可以看出，图中的结点个数并不多，为了便于实现实际需求，可以对此算法进行改进，其改进的基本思想如下：假设以S1作为起始点，以S6作为终点的最短路径已经求出，其路径为S1-S4-S6，则如果需要寻求从结点S4 出发到结点S6的最短路径时，那么就可以参照已经找到的S1 到S6 的最短路径直接求出S4 到S6 的最短路径为S4-S6，即不用重新使用Dijkstra算法求。所以在之前求S1到各顶点的最短路径过程中，要对之前求出的结果进行保存，这样才能通过已经存储的信息迅速得到从源点到目的点的最短路径[8]。改进后的Dijkstra 算法流程图如图2 所示，其中Ds 为始点s 到其他结点的距离，初始状态下为0；Fs表示从源点s到某一目的结点p的最短路径中的前一结点；Di表示检验从所有已标记的结点e到其他未标记的结点f的距离，w（e，f）表示从结点e到f的距离值。

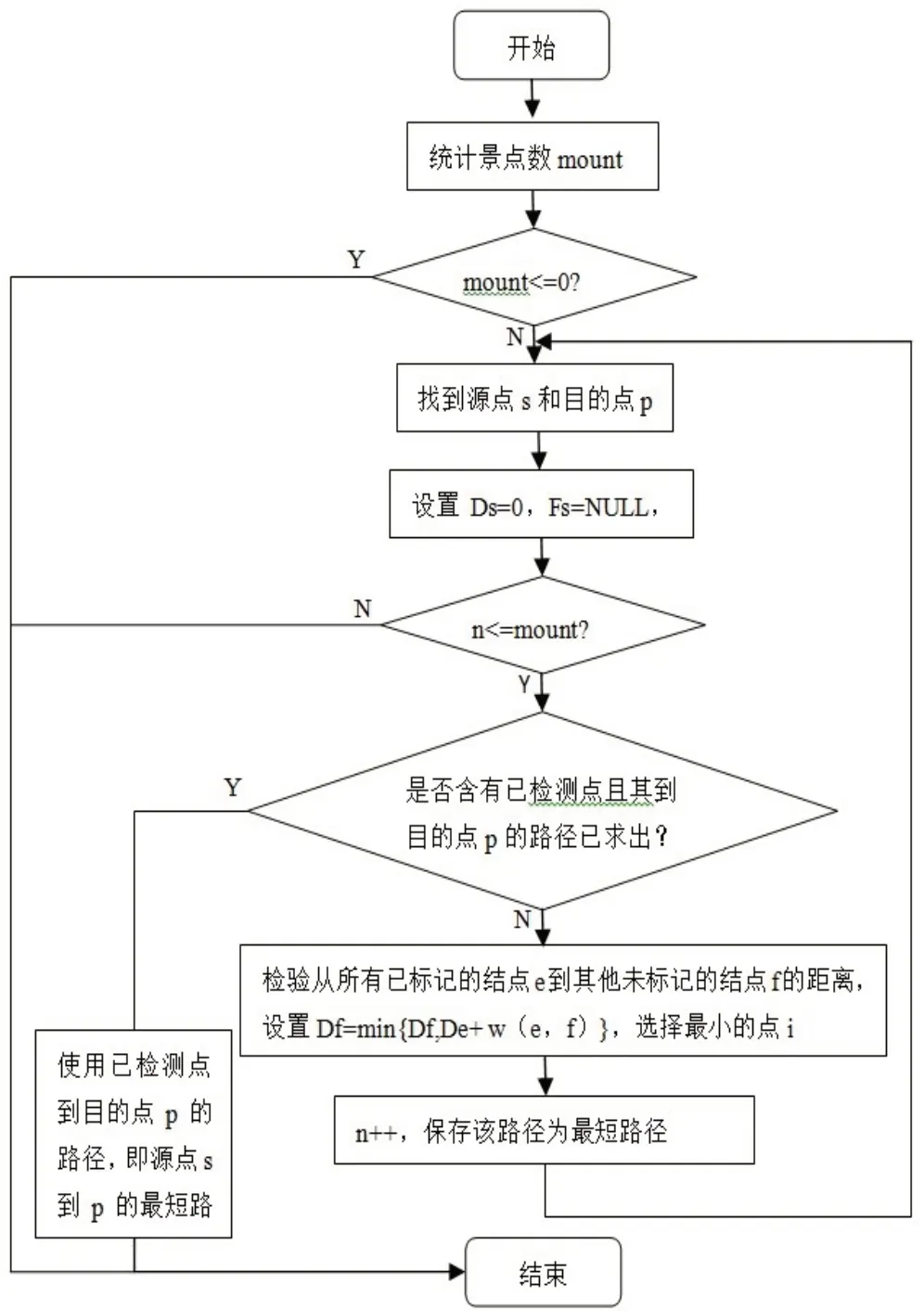
图2 改进后的Dijkstra算法流程图

6 结束语

论文基于Dijkstra 算法对北京部分景点旅游路线进行了规划，首先通过Dijkstra 算法得出了从源点到达各景点的最短路径，然后又对此算法进行改进，通过改进后的算法，能快速得出后续结点的最短路径，并给出了流程图，这样能提升旅游效率。论文建立的最短路径算法可应用于各行各业，尤其是在旅游行业中显得尤为突出，为了便于游客出行，提升旅游质量，找出高效率的旅游路线非常重要，这样才能节约旅游成本，耗费最短时间，使中国旅游行业高质量发展。