深度学习在煤矿水力压裂微震检测中的应用

李 昊,高林生,刘 麟,邵 坤

(1.西安科技大学 能源学院,陕西 西安 710054;2.华北科技学院 矿山安全学院,河北 廊坊 065201;3.华北科技学院 安全工程学院,河北 廊坊 065201)

0 引 言

水力压裂是指通过钻孔注入高压流体,钻孔壁产生破裂并扩展,进而达到强度弱化、增透、应力转移等工程要求[1]。通过这种方法能够使煤岩体产生水压裂缝,从而达到使煤岩体强度弱化和增透的目的,进而提高瓦斯抽采效率[2]。水力压裂过程中会造成岩石破裂,岩石破裂过程中会向外辐射微震能量。通过微震监测获取微震数据,并对其进行定位、震源机制反演等处理能够获得岩石破裂的情况。进而根据岩石破裂情况调整水力压裂的压裂液、加砂量等工艺,获得更好的水力压裂效果。水力压裂过程中会产生大量的微弱微震信号[3],极大增加了识别微震波形的工作量。同时,煤矿井下监测过程中还会出现大量干扰信号,对微震波形的准确识别造成不同程度的干扰[4]。此外,与页岩、砂岩等致密脆性岩石相比,煤作为非均质较强的特殊软岩,微震信号识别难度更大。

在早期的探索中,人们提出了不同的微震波形自动识别方法,例如长短窗法(STA/LTA)[5]、赤池信息准则(Akaike Information Criteria,AIC)[6]。之后也有人联合使用几种方法进行微震波形自动识别或者改进原方法[7-8]。这些波形识别方法都是利用一个或几个统计特征进行的[9],特征的阈值需要人为设定,很难找到一个完美的阈值进而同时提高召回率和准确率[10]。另外,这2种方法对于信噪比较高的波形能够达到较好的识别效果,但是对于低信噪比波形识别效果较差[11]。朱权洁等利用分形技术识别微震波形,但主要针对爆破、岩石破裂等信号,对于煤矿井下水力压裂微震波形识别效果不得而知[12]。为了在尽量减少误识别的前提下增加对微震波形的检测能力,很多学者尝试使用模板识别的方法。这种方法大幅度的增加了检测到的微震数目,但是该方法极大的依赖于已有微震模板,对于因种种原因没有模板的微震,尽管信号很强,也会被该方法漏识别[13]。

进入90年代,SVM等机器学习方法被应用到微震领域,然而随着神经网络层数增加,易出现梯度扩散、过拟合等问题。近几十年来,计算机技术迅猛发展,使得机器学习被应用到实际中[14]。日益成熟的机器学习算法和强大的计算能力,提供了将过去积累的大量数据利用起来的可能。谭文侃、汤志立等对机器学习算法进行了改进[15-16]。大多数研究通过选取多个特征,并利用机器学习方法进行波形识别,在微震波形识别方面取得了一定的成就[17-18]。但方法未深入到深度学习领域中。

近年来,深度学习和人工智能技术快速发展,在地震学领域获得一系列成功应用。卷积神经网络是深度学习中一种常用的计算方法,最先应用于信号处理识别方向[19]。其权值共享的特点使得本身拥有更深网络层数,提取特征的能力大大提高[20]。在使用大量标签数据进行监督学习之后,训练好的模型通常在一些与训练数据相似的测试数据集或者研究区域具有可媲美甚至超过传统方法的效果[21-22]。不过,深度学习方法实用化的关键在于模型能否达到比较高的泛化能力,即是否能在训练样本以外的数据上也取得不错的效果。得益于海量的数据集,经过预处理后输入深度学习模型,一部分深度学习算法模型取得了较高的泛化能力[23-24]。近年来,深度学习卷积神经网络被引入至地震、油气、岩爆等方面的微震波形识别[25-27]。深度学习方法在上述方面已经展现出了优于传统方法的波形识别能力,煤矿井下水力压裂方面却鲜见研究。

文中对山西某矿水力压裂微震监测数据进行加噪和平移预处理,作为深度学习CNN模型的训练和测试数据,搭建适用时域图像和小波图像CNN模型。对比分析2种深度学习模型与传统的STA/LTA和AIC微震识别方法识别水力压裂微弱微震事件的优劣,从而为煤矿井下水力压裂的弱微震事件识别提供一种新的方法。

1 微震波形CNN模型

1.1 CNN模型工作原理

CNN模型是深度学习中一种常用计算方法,能自动从图像中提取抽象特征,把握波形整体信息,从而实现对数据进行分类。煤矿水力压裂微震数据包含大量微弱微震信号,这个特点使得深度学习模型适用于该数据微震波形识别。训练开始前需要对深度学习模型的初始化权值矩阵Wl进行设定：批次值(batch-size)为128、最大迭代次数为57,初始学习率η为0.000 5。若测试精确率连续3次未提升,学习率η降低为原来的一半。训练过程主要包括波形向前传播与误差反向传播。

首先是波形向前传播。训练时从数据集的一个批次中取出一个数据x,将该数据输入至神经网络输入层。在向前传播经过各个层和函数的过程中,数据会输出不同大小的特征图或向量。输入层输出为RGB三通道图像x,卷积计算或者全连接层作用后输出zl,批量标准化函数作用后输出N,激活函数σ激活后输出al。公式(1)是经过激活函数激活后再经过卷积作用的输出。公式(2)是经过批量标准化函数作用后再经过激活函数作用后的输出。

zl=Wlal-1

(1)

al=σ(Nl)

(2)

然后是误差反向传播。根据神经网络的输出和标注y,使用损失函数计算损失值C。再计算损失值C对神经网络输出层delta误差δl,利用相邻层之间δl递推公式求得每一层δl。

如果l+1层是卷积层,那么l层δl误差为

δl=δl+1·ROT180(Wl+1)·σ′(al)

(3)

如果l+1层是池化层,那么l层δl误差为

δl=upsample(δl+1)·σ′(al)

(4)

如果l+1层是全连接层,那么l层δl误差为

δl=(Wl+1)Tδl+1·σ′(al)

(5)

式中 ROT180为将矩阵顺时针旋转180°;upsample为上采样操作。

再利用每一层δl求出损失函数对该层参数的导数∂C/∂W。将一个批次内所求层的所有导数相加(初始化为0),根据梯度下降法更新参数,参数更新公式为

其中后两个词“眉眼”“眉宇”与第一个词“眉目”在义项① “借指容貌”上是义项对应的同义词关系。[注] 葛本仪：《现代汉语词汇学》， 济南:山东人民出版社， 2004年， 第202-207页。三个词互相对应的这个义项恰好也都是借代意义。

(6)

参考经典“LeNet-5”[28],搭建用于识别煤矿井下水力压裂微震波形的二维CNN深度学习模型,如图1所示。图中上方数字从上到下分别为特征图的长、宽、深度,下方数字从上到下分别为卷积核的深度和数量。卷积核参数是深度学习模型中至关重要的部分,卷积核的长和宽都为3×3(像素),步长都为1(像素),全部采用0填充方式。池化作用会导致特征图的长和宽逐渐减小,提取足够的信息就需要更多的特征图,所以卷积核的深度和数量随着模型层数的增加而逐渐提高。

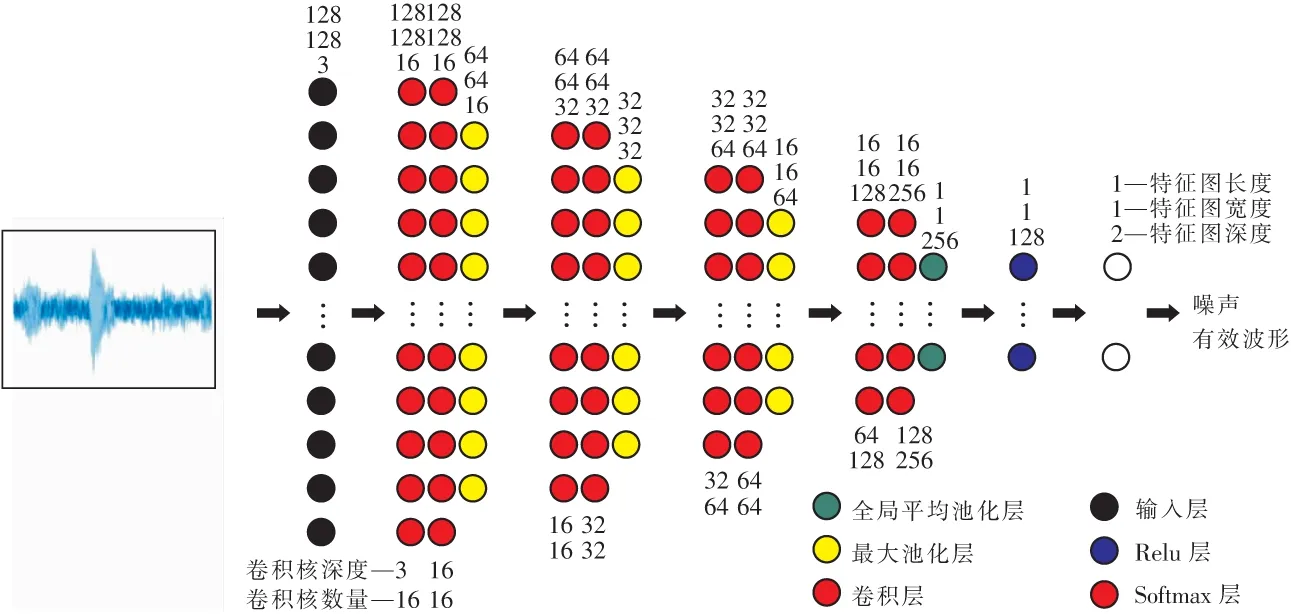
图1 水力压裂微震波形检测的二维CNN模型结构Fig.1 Two-dimensional CNN model structure for microseismic waveform detection of hydraulic fracturing

模型结构从前往后依次为：输入层、3层卷积层和最大池化层、1层卷积层和全局平均池化层、Relu层、Softmax层。输入层输出RGB三通道图像数据,大小全部降维到128×128,全局平均池化层将特征图转变为256×1的列向量,之后Relu层将256×1的列向量转变为128×1的列向量,最后Softmax层将128×1的列向量转换为2个0～1的数值。这2个数值代表该波形片段是微震波形和背景噪声的预测概率,将用于识别波形片段是否为微震波形或者背景噪声。

1.2 数据预处理

山西某煤矿6号煤层为突出煤层,用水力压裂增透煤层,治理消除煤与瓦斯突出危害,在此基础上开展瓦斯防治和抽采工作。通过微震监测获取水力压裂裂缝扩展情况,评价水力压裂工艺效果。采集数据所用微震传感器灵敏度为200 V/(m/s),频带范围为4.5～1 500 Hz;系统采样率为4 k。在钻孔中安装传感器,最大程度屏蔽噪声。深度学习模型需要大量数据样本以避免过拟合,因此选取了4 d的水力压裂微震监测数据,为深度学习模型提供了大量的训练样本。

训练数据的质量对一个良好的深度学习模型起重要作用。从原始数据中截取5 860条含有微震波形的片段,标注为1;排除微震波形后随机截取8 341条背景噪声片段,标注为0。对挑选后的数据仍需要再次检查,更正明显的标注错误,尽可能减少人工标注错误。数据集中微震事件震级范围主要在-3～0级(2～5.410J),微震波形持续时间最长可达到1.2 s。为了尽可能地将不同震级微震的波形包含在波形片段内,将深度学习模型滑动窗口长度和步长都设定为1.5 s。

为了数据集更加适应深度学习模型,需要进行加噪处理。首先需要计算被加噪波形能量,然后增加与该能量固定比例能量的噪声,为了保证数据的准确性,微震波形总体加噪程度偏低。为使加噪后波形数量和背景噪声数量大致相同,对所有微震波形各自加噪自身原有微震波形能量的1/32,1/33,…,1/48,共17种不同程度噪声;对所有背景噪声各自加噪原有背景噪声能量的1/14,1/15,…,1/25,共12种不同程度噪声。原始微震波形和加噪层度1/32的波形对比如图2(a)和图2(b)所示。不同加噪程度的微震波形占加噪后总微震波形数量的1/18。不同加噪程度的背景噪声占加噪后总背景噪声数量的1/13。

图2 不同加噪和平移程度时域微震波形Fig.2 Time domain microseismic waveform with different degree of noise adding and translation

微震波形加噪程度要低于背景噪声。这是因为数据集内微震波形信噪比差别较大,如果以高信噪比微震波形为标准加噪,那么将其加噪至微弱波形所需能量比就比较大。然而,以这较高能量比对低信噪比微震波形进行加噪,低信噪比微震波形就会被背景噪声淹没成为背景噪声。数据加噪测试表明,信噪比最低的波形加噪程度大于等于1/31时便几乎被背景噪声淹没,所以微震波形加噪最高选为1/32。背景噪声在加噪过程中不存在被背景噪声淹没的情况,所以加噪程度相对偏大。

对数据加噪和平移预处理后,最终得到102 546条微震波形数据和101 123条背景噪声数据。

图3是与图2对应的小波变换图像,可以看出,加噪前后图像在100 Hz的低频部分几乎没有变化,但在100 Hz以上的高频部分有更多分布。无论数据如何平移,微震波形总是在100 Hz左右有较为明显的分布,且在时间上与微震波形对应。

图3 不同加噪和平移程度微震波形小波变换Fig.3 Wavelet transform with different degree of noise adding and translation

有些原始背景噪声(图4(a))与微震波形类似。从小波图像来看(图4(c)),这类波形在100 Hz左右的低频部分有较为明显的分布,这个特点与微震波形较为类似。然而,低频部分的分布是近乎连续的,这类波形是工人井下作业时造成的干扰信号,属于背景噪声。对原始背景噪声加噪1/25的小波图像(图4(d))可以看出,加噪后波形在100 Hz以下的低频部分有了更多的分布,明显区别于微震波形。

图4 背景噪声图像Fig.4 Images before and after adding background noise

1.3 2种深度学习模型搭建

深度学习模型对微震波形的识别流程如图5所示。首先,对原始数据进行加噪、平移等预处理,生成训练集、测试集和待检测集图像。然后,从微震波形和背景噪声中随机选取80%,20%的数据用于深度学习模型的训练和测试。如果模型表现良好,则保存其性能。如果模型表现不佳,则需要对模型参数或数据集进行调整,直至模型性能达到预期。使用性能良好的深度学习模型来检测待检测数据,并将输出结果。对于每个波形片段,根据其被识别为微震波形还是背景噪声,输出1或0。由于通常需要4个微震波形才能定位微震事件,因此需要根据同一时间窗口内含有微震波形通道数是否大于3为判据进行微震事件的判断。如果被判定为微震事件,将该事件对应的所有通道波形存储,并从中提取出含有微震波形的通道数据,然后将这些数据与存储的波形进行对比。如果不是微震事件,则该数据被丢弃。

图5 CNN模型的煤矿井下水力压裂诱发微弱波形识别流程Fig.5 Identification process of weak waveform induced by hydraulic fracturing in coal mine based on CNN model

适用时域图像、小波图像的CNN模型训练测试正确率和损失函数分别如图6(a)和图6(b)所示。通过2种图像识别的训练、测试数据集的准确率都达到了99%以上,损失函数都在0.02以下。2种方法测试集准确率和损失函数在起始阶段出现了震荡,这是因为初始设置的部分模型初始参数值(权值矩阵、学习率等)与最优值差别较大。但随着训练的不断进行,模型参数逐渐向着最优值靠近,之后明显震荡消失。最终保存使用的是训练效果最好的模型。

图6 训练、测试准确率与损失函数Fig.6 Accuracy and loss functions of training and testing

2 波形识别结果

2.1 事件准确率和召回率

分别使用深度学习训练好的2个模型检测一个小时连续水力压裂数据,并将检测结果与传统AIC和STA/LTA微震事件检测方法的结果作对比。在这一个小时的数据中,共确定了328个事件。以这328个事件作为对比,分析时域CNN模型、小波CNN模型、STA/LTA和AIC 4种方法微震事件识别精确率和召回率。精确率Pe和召回率Re的定义分别为

Pe=Tp/(Tp+Fp)

(7)

Re=Tp/(Tp+Fn)

(8)

式中Tp为真正例,即算法识别的微震事件为真实微震事件,反之为假正例Fp;Tn为真反例,即算法识别的背景噪声是真实背景噪声,反之为假反例Fn。精确率高代表误检率低,召回率高说明算法漏检率低,只有两者都高时模型或者算法才拥有实用价值。对滤波前后检测数据进行检测,滤波器阶数为128,各种方法滤波前的检测结果分别见表1和表2。无论滤波前后,精确率和召回率均为时域CNN模型>小波CNN模型>AIC>STA/LTA。时域CNN模型的正确率和召回率是最高的,且随着波形信噪比的提高,各种方法的精确率、召回率都有了不同程度的提高。

表1 滤波前STA/LTA,AIC和CNN模型识别精确率和召回率Table 1 Identification accuracy and recall rate of STA/LTA,AIC and CNN models before filtering

表2 滤波后STA/LTA,AIC和CNN模型识别精确率和召回率Table 2 Identification accuracy and recall rate of STA/LTA,AIC and CNN models after filtering

微震波形与背景噪声在幅值、频率等方面有许多不同之处。AIC,STA/LTA方法主要是依靠单一的幅值信息(幅值大小和变化),缺少对波形总体信息的提取和分析。CNN模型将一张图像看作是一个个像素组成的矩阵,对图像的分析就是对矩阵的数字进行分析,而图像特征就隐藏在这些数字规律中。该模型通过图像向前传播和误差反向传播使模型参数逐渐向最优值靠近,最终获得优于AIC,STA/LTA的波形识别能力。

时域CNN的识别微震事件召回率和精度是最高的,这是因为时域图像由传感器采集的数据直接转换,内部包含最丰富的原始信息。小波图像是经过原始数据变换之后转换成的图像,不可避免的会丢失部分原有信息,所以时域CNN模型优于小波CNN模型。

水力压裂常见的背景噪声信号是电压噪声和水流噪声,两者都有明显的起跳点,容易被传统方法误判定为微震事件,影响压裂效果的评价。时域CNN方法能够准确识别这2种噪声。上述2种噪声信号在时域、频域方面又存在明显区别。如图7(a)所示,电压噪声信号波形信号特点是在每个通道同一时间只有一道垂直向上的信号;如图7(b)所示,由于裂缝贯通后的水流噪声持续时间较长,水流噪声波形信号在较长时间内存在连续频带分布。对比2种噪声的小波图像,进一步证明了上述规律。如图7(c)所示,电压信号在1 000 Hz内有较为明显的分布,且分布频带范围较广。如图7(d)所示,水流噪声500 Hz以内有较为明显的分布,且持续时间较长。

2.2 水力压裂微震事件识别实例

选取15 s的水力压裂微震数据,共12个通道的波形片段,分别用时域CNN模型、小波CNN模型、AIC,STA/LTA 4种方法识别微震事件。微震事件识别标准是至少4个通道含有微震波形,而各通道内微弱微震波形的识别是关键。图8(b)、图8(c)中事件是4种方法共同识别出的事件,其中C4,C6,C7,C8和C10通道都含有明显的微震波形,容易达到至少4个通道含有微震波形的识别标准。图8(a)是时域CNN方法识别出,但其他3种方法未识别出的事件,其中C6,C8和C10通道存在微弱微震波形,识别难度较大,只有时域CNN方法识别出C6,C8,C10通道的微弱波形,加上较为明显易于识别的C7波形,从而达到至少4个通道的微震事件识别标准。由此看出,在微弱波形识别方面,时域CNN方法要优于小波CNN方法,AIC,STA/LTA。

图9是2种深度学习模型分别与STA/LTA,AIC联合识别在一个小时连续数据中识别出真实微震事件的对比。时域CNN模型、STA/LTA,AIC在一个小时连续数据中,联合识别出257个真实微震事件。其中,3种方法共同识别出真实微震事件占比约为50%,时域CNN模型单独识别的真实微震事件占比约为36%,时域CNN模型未识而被其他2种方法识别的真实微震事件占比约为14%。小波CNN模型、STA/LTA,AIC在一个小时连续数据中,联合识别出229个真实微震事件。其中,3种方法共同识别出真实微震事件占比约为52%,小波CNN模型单独识别的真实微震事件占比约为28%,小波CNN模型未识别而被其他2种方法识别的真实微震事件占比约为20%。

图9 CNN模型、STA/LTA,AIC识别真实微震事件占比Fig.9 Proportion of real microseismic events identified by CNN model,STA/LTA and AIC

时域CNN模型或者小波CNN模型与STA/LTA和AIC共同识别出的真实事件大多是较为明显的真实微震事件。2种CNN模型识别出但STA/LTA,AIC未识别出的事件大多为真实微弱微震事件。在微弱真实事件识别方面,CNN深度学习模型拥有优于传统方法的识别效果,且时域CNN模型优于小波CNN模型。

3 结 论

1)将水力压裂数据进行加噪和平移预处理后,分别转换为时域图像、小波图像。然后分别输入CNN模型进行训练,2种CNN模型训练、测试的准确率都达到99%以上,损失函数都在0.02以下,为微震事件识别提供了一种更优的方法。

2)在识别中发现,水力压裂常见的背景噪声有电压噪声和水流噪声。电压噪声波形虽然持续时间较短,但有明显的起跳点;水流噪声波形持续时间较长,但起跳点不明显。STA/LTA,AIC,小波CNN模型较难识别这2种噪声,时域CNN模型能够识别。

3)在微震事件识别精确率和召回率方面,时域CNN模型优于小波CNN模型,优于AIC,优于STA/LTA。能够提取抽象特征的CNN深度学习模型拥有优于传统方法的识别效果。小波变换会使图像不同程度的丢失掉部分信息,所以时域CNN模型具有更好的微震事件识别效果。研究内容为煤矿井下微弱波形识别提供一定参考价值。