铲削式翅片散热器空气侧传热流动特性试验研究
白晓春,朱 超,王 绿,林子博,苗阿乐,杨 鹏,刘迎文
(1.国网陕西省电力有限公司电力科学研究院,陕西 西安 710000;2.西安交通大学 热流科学工程教育部重点实验室,陕西 西安 710049)
0 引 言
变压器作为户内变电站的重要组成设备,其散热性能的优劣会影响到电网运行的可靠性与稳定。目前变压器所采用的散热方式主要是风冷散热,即在变压器上加装片式散热器,通过与主变室内空气换热将变压器热量带走。片式散热器能够保证变压器处于合适的工作温度范围,防止因变压器超温引起事故的发生。因此,强化变压器片式散热器的换热效率,提高散热器的散热性能对变压器的安全稳定运行具有重要意义。
针对强化变压器片式散热器的散热效率,许多学者从各个方面进行了大量研究,主要聚焦在散热片的结构参数优化设计(如改造角度、散热片数量、散热板穿孔直径、翅片形状等)[1-6]、散热油的流量分布规律[7-11]、散热器表面材料改进[12-13]、外界冷却条件强化[14-16]等方面。其中,许多研究通过对散热器结构及相关参数进行优化改进,进而实现换热性能的强化。梁义明等通过仿真分析成组散热器整体结构、片式散热器散热片数量等因素的变化对散热器的影响,发现当整体改造角度为20°且片式散热器的散热片最佳数量为25片或26片时,散热器的散热性能最佳[1]。邵志伟等利用CFD方法研究散热片数对散热效率的影响,发现散热片数从9片增加到18片时,散热效率从43.94%增大到61.06%[2]。戚美等建立片式散热器模型,研究散热板穿孔直径对散热板的辐射换热、对流换热和综合换热性能的影响,当安装孔径为18 mm时,两侧散热板的综合传热性能分别提高了25.46%和28.76%[3]。MAHDI研究4种不同翅片形状对片式散热器内部温度和流体流动的影响,与标准设计的矩形翅片相比,上宽下窄的梯形翅片具有最佳的换热性能[4]。刘丹丹等利用Fluent软件对比不同散热器散热中心高度对变压器流体温度和速度的影响,通过增加散热器散热中心高度可以有效提高变压器油的流速、降低变压器温升[5]。
目前变压器散热器的主要结构形式是传统的片式散热器。随着城市居民用电负荷的日益增加,现有片式散热器的散热性能已无法满足变压器在高温大负荷运行条件下的散热需求。铲削式飞翼形翅片作为一种新型结构翅片,目前已广泛应用在数据中心、重型卡车的散热器中。LONG等对铲削式翅片换热器的加工过程进行了介绍,认为其接触热阻可以忽略,并对铲削式翅片的热工水力特性进行详细研究,在几何形状相似时铲削式翅片比波纹型翅片的换热性能更好,因此铲削式翅片具有十分广阔的应用前景[17-18]。文中针对现有片式散热器散热效率低的问题,设计一种铲削式翅片与片式散热器结合的新型散热器,首次将铲削式飞翼形翅片应用于变压器散热器。此外搭建散热器的流动换热综合测试平台,以空气为散热器两侧的流动介质,开展散热器流动换热性能的试验研究,并通过试验数据拟合了铲削式翅片的换热与阻力关联式。
1 试验装置与系统
1.1 铲削式翅片散热器结构
根据常见变电站片式散热器的结构尺寸,制作一个近似等比例缩小的铲削式翅片散热器样件。该散热器属于板翅式结构换热器,由6排管道、12排翅片、前后端盖及上下盖板组成。常见的平直、波纹等翅片结构的换热器,其翅片通过粘接或者钎焊的形式与管道连接,不可避免地存在接触热阻。铲削式翅片散热器最大的特点是,其翅片是从管道壁面直接铲削出来,加工时翅片与管道一体成型,不存在接触热阻,因此具有较高的传热效率。
铲削式翅片散热器的单排管道及翅片结构如图1所示,管道截面尺寸280 mm×173 mm(长×宽),管道被分成12个小通道,两两之间由隔断面隔开,单个通道截面13.5 mm×6 mm(长×高)。翅片为飞翼形结构,翅距3 mm,翅厚0.3 mm;单个翅片的横截面接近正切函数曲线形状,高度约3.5 mm;纵向看翅片形状接近正弦函数曲线,翅片流道分为等长的4段,每段长41 mm,每段之间的间隔为2.3 mm。试验中管内流动的介质用高温空气来替代导热油,管内侧下文也称为高温侧;翅片侧流动的介质是冷却空气,下文称为低温侧。

图1 铲削式翅片散热器管道及翅片结构Fig.1 Structure of the shovel-fin heat exchanger
1.2 试验系统
针对铲削式翅片散热器的结构特点,设计并搭建流动换热综合测试平台,试验系统原理示意图如图2所示。试验系统主要由闭环的高温空气通道、开环的低温空气通道、PID自动控制系统和数据采集系统组成。高温侧为散热器的管内侧,离心风机带动整个闭环管道的空气循环,管道内低温空气从风机流出后流经加热器被加热成指定温度的高温空气,随后流经较长的混合管道,其中经过数个微孔板强化混合,到达散热器管道侧入口。高温空气在散热器与低温空气换热后流经喷嘴回到风机入口,随后进入下一次循环。低温侧空气来自室内,通过入口控温换热器与来自冷热水机组的介质换热,从而达到控制入口温度的目的,随后低温空气进入散热器翅片侧与高温空气换热,换热后到达风机口排出至室外。
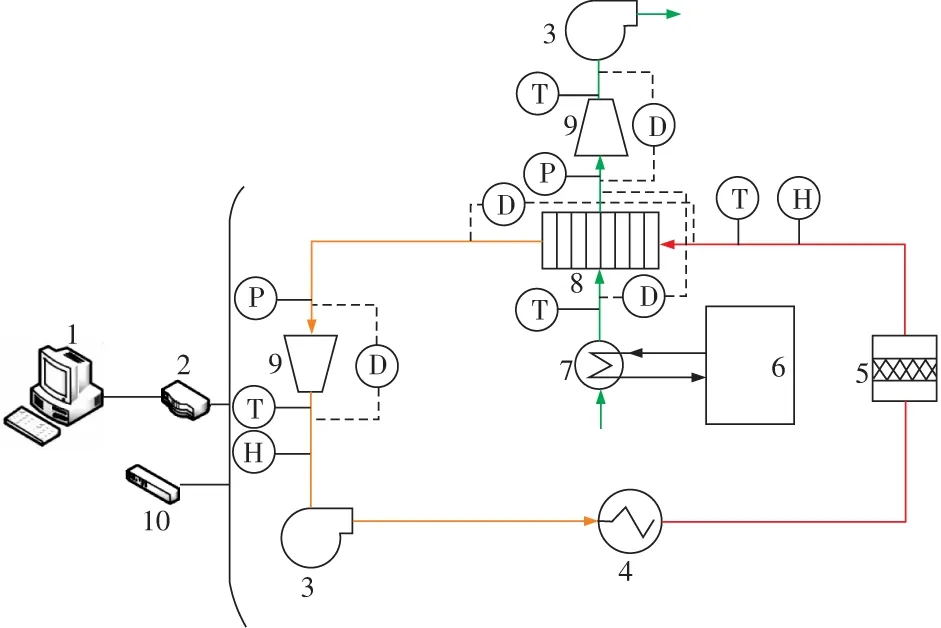
1-计算机;2-数据采集器;3-离心式风机;4-加热器;5-混合管道;6-冷热水机组;7-换热器;8-铲削式翅片散热器;9-喷嘴流量计;10-PID控制系统;T-温度测点;P-绝压测点;H-相对湿度测点;D-压差测点图2 试验系统原理示意图Fig.2 Schematic diagram of the experimental system
高温侧和低温侧通道均布置有喷嘴流量计,同时在高温侧出入口、低温侧出入口布置多个温度、湿度、压力及压差测点。PID控制系统根据布置在高温侧入口的热电偶反馈的温度值来调节加热器功率,从而控制管道侧入口空气温度。低温侧入口空气温度通过冷热水机组和入口的换热器来调节控制。高温侧和低温侧的空气流量通过PID控制系统、风机变频器控制风机转速来调节。所有测点的数据均由数据采集器实时采集并传送到计算机保存,由计算机汇总和处理试验数据。
所有的试验管道均包裹保温材料以减少试验台向周围环境的漏热。温度由美国OMEGA公司的T型热电偶测量,精度为±0.1 ℃;相对湿度由相对湿度变送器测量,型号为E+E99-1-FP6AD 8025,测量范围:0~100%RH,测量精度:±2%(0~90%RH),±3%(>90%RH);压力由绝压传感器测量,型号为MICROSENSER MPM4730,量程为0~150 kPa,精度为±0.15%;压差传感器型号为日本横河EJA110,量程为0~1 000 Pa,精度为±0.25%。数据采集器为安捷伦34 970 A。
试验采用控制变量法,每组工况都保持散热器某一侧空气的流量及进口温度不变,改变另一侧空气的流量,得到一系列数据点。
2 数据处理
2.1 试验数据处理
试验中高温侧和低温侧的空气流量通过测量喷嘴前后压力、温度和相对湿度计算得出。利用喷嘴前后的压差值可以计算空气的质量流量,计算见式(1)
(1)
式中mn为喷嘴处空气质量流量,kg·s-1;C为流量系数,在试验条件下取为0.97;Dn为喷嘴喉部直径,m;ρnf为喷嘴后空气密度,kg·m-3;Δpn为喷嘴前后压差,Pa。
则喷嘴处的体积流量为
Vn=3 600mn/ρnf
(2)
式中Vn为喷嘴后湿空气体积流量,m3·h-1。
在试验数据采集开始前,先对高温侧的空气进行除湿处理,具体步骤为:开启加热器和风道与环境通风的阀门,将空气的相对湿度调整至10%以内。由于空气的相对湿度较低,因此可以将高温侧空气视为干空气,高温侧换热忽略冷凝潜热,则高温侧的换热量计算式如下
Qh=1 000×mh(cp,hithi-cp,hotho)
(3)
式中Qh为高温侧换热量,W;mh为高温侧质量流量,kg·s-1;cp,hi为高温侧入口空气比热容,kJ·kg-1·K-1;thi为高温侧入口温度,K;cp,ho为高温侧出口空气比热容,kJ·kg-1·K-1;tho为高温侧出口温度,K。
同理,低温侧的换热量计算式如下
Qc=1 000×mc(cp,cotco-cp,citci)
(4)
式中Qc为低温侧换热量,W;mc为低温侧质量流量,kg·s-1;cp,ci为低温侧入口空气比热容,kJ·kg-1·K-1;tci为低温侧入口温度,K;cp,co为低温侧出口空气比热容,kJ·kg-1·K-1;tco为低温侧出口温度,K。
因此,散热器的平均换热量Q为
Q=(Qh+Qc)/2
(5)
高、低温侧的热平衡误差为
ε=|Qh-Qc|/Qc×100%
(6)
当高、低温侧的热平衡误差小于等于5%时,试验结果视为准确有效。
2.2 换热关联式拟合
对于单侧工况不变的试验,可以采用Wilson法对传热过程中的热阻进行分析并拟合关联式[19]。在生产和研究中,通常采用无量纲换热准则方程来计算翅片侧换热特性,如下式
Nu=aRemPrn
(7)
式中a,m,n为常数,需要通过试验数据分析得到,一般而言,当流体被加热时,n=0.4。按照换热器结构将总传热热阻分离为3部分,即管内侧对流换热热阻、壁面导热热阻和翅片侧对流换热热阻,见式(8)
(8)
式中ht,hf分别为管内侧、翅片侧的对流换热系数,W·(m2·K)-1;At,Af分别为管道侧、翅片侧的对流换热面积,m2;Rwall为壁面导热热阻,m2·K·W-1。
无量纲数Nu和对流换热系数有如下关系
Nu=hA/De
(9)
式中De为当量直径,m。
当管内侧工况不变时,可认为管道侧对流传热热阻和壁面导热热阻不变。在计算管道侧Nu中,试验中高温管道侧空气的速度及物性参数符合Gnielinski公式的使用条件,因此采用其计算管道侧的Nu,Gnielinski见式(10)
Nu=
(10)
在改变低温侧空气流量的试验中,管内侧的工况基本不变,可以认为管道与壁面的热阻为常数,记为R0,因此式(8)可变成
(11)
移项后两边取对数可得
(12)
式中Dc为翅片通道当量直径,m;Ac为翅片换热面积,m2;λc为翅片侧空气导热系数,W·(m·K)-1。
将试验数据代入线性方程,通过最小二乘法即可求出m和C。
2.3 阻力关联式拟合
翅片通道流体压降和Darcy阻力系数f具有如下关系
(13)
式中L为流体通道长度,m。
在低雷诺数的条件下,可以认为摩擦阻力只是雷诺数的函数,摩擦系数f具有如下形式
(14)
其中Cf和mf为常数,将式(14)代入式(13)得

(15)
方程两边取对数,则有
(16)
同样将试验数据代入,然后使用最小二乘法得到mf和Cf。
3 结果与讨论
3.1 换热特性
试验中设置了2组不同工况来研究低温侧流量变化对铲削式翅片散热器换热特性的影响。工况一:高温侧入口空气温度为75 ℃、流量为234 m3·h-1;低温侧入口空气温度为25 ℃,流量从103.7 m3·h-1变化到235.5 m3·h-1。工况二:高温侧空气流量变为190 m3·h-1,其他条件不变。
图3为换热量随低温侧流量变化的结果,可以看到,换热量随着低温侧流量的增大而增大,2种工况下的换热量变化趋势相同。高温侧流量为234 m3·h-1时,随着低温侧流量从103.7 m3·h-1变化到235.5 m3·h-1,换热量从804.2 W增大到1 158.9 W,增大了44.1%。高温侧流量为190 m3·h-1时,随着低温侧流量增大,换热量从706.9 W增大到1 020.1 W,增大了32.5%。高温侧流量为234 m3·h-1时的换热量整体大于190 m3·h-1时的换热量,因为大流量下单位时间参与换热的热空气更多,强化了通过壁面的对流换热,因此换热量更大。

图3 换热量随低温侧流量变化Fig.3 Variation of heat transfer rate with flow rate of low temperature side
从图3可以看到,随着低温侧流量增大,换热量的增大速率呈现变缓的趋势。低温侧流量较小时,散热器的热阻以翅片侧热阻为主,低温侧流量增大,通过翅片侧通道的冷却空气流量增大,单位时间与高温空气换热的冷空气更多,强化了翅片侧的对流换热,翅片侧热阻减小,因此换热量增大。当低温侧流量增加到较大值时,散热器的主要热阻从翅片侧变成管内侧,受限于管内侧热阻,换热量的增大速率变缓。综合2条曲线的变化趋势来看,可以认为在一定的流速区间内,换热量与流量成线性关系。
为了进一步研究铲削式翅片的换热特性,采用威尔逊法分离热阻,使用最小二乘法拟合得到翅片侧对流换热关联式如下
Nu=0.02Re0.89Pr0.4
(17)
图4为试验数据计算的翅片侧Nu值与拟合的对流换热关联式之间的对比。从图4可以看到,试验值与关联式的吻合度较好,最大误差仅为5.67%。

图4 Nu试验值与关联式拟合值误差对比Fig.4 Comparison of the proposed correlation with the present experimental data on Nu
在拟合翅片侧对流换热关联式时,计算管内热阻和对流换热系数使用的是高精度Gnielinski公式,为了验证这一做法的准确性,文中将拟合关联式及Gnielinski公式分别计算得到的Nu进行对比。固定翅片侧低温空气流量不变,即固定翅片侧热阻不变,变化管道内高温空气流量,分别采用2种方法计算得出管内的Nu,对比结果如图5所示。

图5 2种计算方法的Nu比较Fig.5 Comparison of two calculation methods for Nu
从图5可以看出,随着Re的增大,Nu也随之增大。管道内Re在2 000~5 000范围内变化时,使用拟合的翅片侧对流换热关联式反算的管内Nu与用Gnielinski公式直接计算的Nu吻合度较好,64%的试验数据点误差在5%以内,93%的试验数据点误差在10%以内,因此可认为使用Gnielinski公式计算该试验铲削式翅片散热器管内热阻是合理的。
作者在之前的研究工作[20]中使用CFD仿真计算得到了铲削式翅片在雷诺数范围为1 000~6 000时的对流换热关联式和阻力关联式,该关联式考虑翅片的多个几何尺寸因素,具有较高的准确性,并在文献[21]中得到验证。为了验证通过试验拟合得到的铲削式翅片侧对流换热关联式的准确性,将试验数据代入仿真拟合的换热关联式进行对比。式(18)为仿真拟合的换热关联式,如下
Nu=1.958 85Re-0.174 72×
(FP/Fh)4.638 15(0.5FP/A)Nu1(Ld/L)1.949 67(θ/θv)Nu2
(18)
式中Nu1和Nu2分别为
Nu1=-12.019 81-1.883 76ln(FP/Fh)+
2.460 72ln(Ld/L)-3.182 47ln(θ/θv)
(19)
Nu2=-9.786 09+3.306 92ln(FP/Fh)+
4.689 92ln(Ld/L)-5.704 7ln(θ/θv)
(20)
式中Fp为翅片间距,mm;Fh为翅片高度,mm;Ld为翅片流道长度,mm;L为翅片波长,mm;θ为翅片倾斜角;θv为翅片垂直时角度,即90°。试验样件的翅片间距、翅片高度、翅片流道长度、翅片波长、翅片倾斜角分别为3,3.5,164,6 mm,65°。
对比结果如图6所示。文中关联式计算值与仿真拟合关联式计算值的最大误差为26.66%,平均误差为9.19%。仿真拟合关联式中考虑翅片间距、翅片高度、翅片波长等众多几何参数条件,而在实际中由于换热器翅片加工精度、人为测量翅片参数及试验系统存在的各种误差,加之拟合试验关联式使用的数据点较少,因此使用试验结果拟合出来的关联式计算结果与仿真得到的关联式计算结果存在偏差可认为是合理且正常的。仿真拟合关联式与文中关联式的误差大部分控制在20%以内,因此可认为拟合的翅片对流换热关联式是准确可靠的。

图6 文中关联式Nu与仿真拟合关联式Nu对比Fig.6 Comparison of the proposed correlation data with the correlation proposed by simulation on Nu
3.2 阻力特性
在上一小节设置的试验工况条件下,对铲削式翅片的阻力特性进行研究。低温侧压降与流量的关系,如图7所示,可以看到,低温侧压降随着流量的增大而增大。高温侧流量为234 m3·h-1时,低温侧流量从103.7 m3·h-1变化到235.5 m3·h-1,压降从64.5 Pa增大到248.5 Pa,压降增大了几乎4倍。在高温侧流量为190 m3·h-1时,随着低温侧流量的增大压降也同样增大了4倍。低温侧流量增大时,流经翅片的空气速度更快,空气与翅片的摩擦更剧烈,流动能量损失更大,因此压降增大。此外,可以看到高温侧流量的变化对翅片侧压降几乎没有影响。分析其原因:在相同的低温侧流量下,改变高温侧流量影响的是低温侧流体的温度,而低温流体物性中的密度和粘度随温度的变化较小,因此低温侧压降变化较小。

图7 低温侧压降与流量关系Fig.7 The relationship between pressure drop and flow rate on low temperature side
为了更进一步研究铲削式翅片的阻力特性,同样对现有试验数据采用最小二乘法拟合阻力系数关联式,见式(21)
f=2.62Re-0.35
(21)
图8对比了拟合阻力关联式计算的压降值与实测的压降值,2条曲线重合度较高,所有数据点误差均在5%以内,最大误差仅为3.32%,说明拟合的阻力关联式准确性较高。
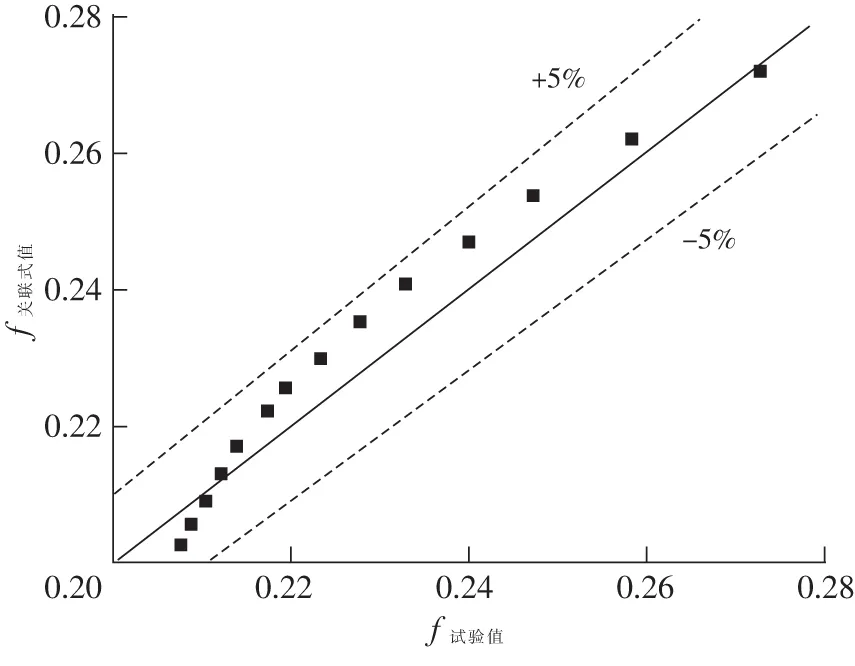
图8 拟合阻力关联式计算压降值与实测压降值对比Fig.8 Comparison of the pressure drop calculated by proposed correlation with present experimental pressure drop data
同样地,之前通过仿真也拟合了铲削式翅片的阻力关联式如下
Nu=0.359 48Re-0.175 1×
(FP/Fh)4.409 85(0.5FP/A)f1(Ld/L)1.925 16(θ/θv)f2
(22)
式中f1和f2分别如下
f1=-11.146 63-1.783 21ln(FP/Fh)+
2.260 94ln(Ld/L)-3.229 96ln(θ/θv)
(23)
f2=-10.002 17+3.210 82ln(FP/Fh)+
4.728 97ln(Ld/L)-5.606 27ln(θ/θv)
(24)
同样地,将试验测试得到的翅片侧Re和翅片结构尺寸参数代入式(22)中得到的f值,并与文中拟合的关联式计算的f值进行对比,结果如图9所示,文中试验关联式计算值与仿真拟合关联式计算值的平均误差为16.36%。同上述换热关联式一样,文中试验拟合的阻力关联式与仿真拟合的关联式存在误差,出现这样误差的原因同样也归结为试验拟合关联式数据点较少、实际换热器结构参数测量误差、试验测试人为误差及仿真拟合关联式使用条件考虑要素更多等。从2个关联式计算的数据点平均误差来判断,可认为试验数据拟合的关联式是较为准确可靠的,在工程中可用于分析。
4 结 论
1)当管道侧流量为190 m3·h-1,翅片侧流量从103.7 m3·h-1增大到235.5 m3·h-1时,换热量从706.9 W增大到1 020.1 W;当管道侧流量为234 m3·h-1,翅片侧流量同样在上述范围内变化时,换热量从804.2 W增大到1 158.9 W。散热器的换热量与翅片侧空气流量近似成线性关系。
2)当管道侧流量为190 m3·h-1,翅片侧流量从103.7 m3·h-1增大到235.5 m3·h-1时,翅片侧压降则从62.33 Pa增加到250.11 Pa;当管道侧流量变为234 m3·h-1,翅片侧流量同样在上述范围内变化时,翅片侧压降则从64.55 Pa增大到248.46 Pa。管道侧流量变化对翅片侧压降几乎没有影响。
3)在翅片侧空气流量对应的雷诺数范围内,通过试验拟合得到翅片侧的对流换热关联式Nu=0.02Re0.89Pr0.4,和流动阻力关联式f=2.62Re-0.35,与仿真拟合的关联式相比,换热关联式平均误差为9.19%,阻力关联式平均误差为16.36%,具有较好的可靠性。

