测向天线基线选择对测量精度影响的研究

王晨航，高加健，徐 璐，张一嘉

（1.浙江理工大学信息科学与工程学院，浙江 杭州 310018；2.四川九洲电器集团有限责任公司，四川 绵阳 621000）

0 引言

近年来，无线通信技术正在快速发展，无线电侦察测向以及精准定位正逐渐成为影响战争胜负的关键因素。无线电测向是在空间中利用接收的信号信息来测定辐射源信号的到达方向，属于无源测向技术［1］。无源测向是指由测向系统对辐射源进行测向时，测向设备并不需要通过自身先发射一个助于测向的电磁波信号，所以无线电测向的隐蔽性更强［2］。随着测向设备在海、陆、空等平台的广泛应用，由阵列应用环境不同导致的阵列类型更加多样，本文针对不同的项目需求，通过仿真分析天线阵列分布下的天线基线情况以求得更加良好的测向精度，为工程应用提供支持。

对于测向系统来说，影响测向精度的原因很多，包括外部原因如噪声干扰和障碍物导致的反射波，内部原因如自身通道误差、天线设备互耦等。姜志成分析了干涉仪测向的误差情况，并提出了相位校准方法，但未对不同天线阵列排布对测向系统的影响进行分析［3］；吴启星等人结合了卡尔曼滤波对误差分析模型进行了优化，使误差分析更为准确真实，但是该研究的测向模型没有考虑一般情况下虚拟基线的使用［4］。段国文等人对常用天线阵列的测向精度情况进行了分析［5］，党浩淮等人在其基础上增加了天线相位误差对天线测向的关系［6］，但是均缺少了阵列排布间距对测向精度误差的影响分析。

设计天线阵列时，需要综合考虑天线尺寸、可应用频段等因素，选择合适的天线阵元和分布间距，以满足系统需求［7］。基于此，本文构建了针对五元线阵和五元均匀圆阵的干涉测向模型，主要工作如下：1）采用基于平行虚拟基线选择完成测向解模糊的方法，将相位测量值与测向理论数据库进行相关查找，相关最大值所对应的角度即为来波方向；2）分析了测向过程中的频率灵敏度和角度灵敏度所引起的测向误差；3）通过MonteCarlo 仿真，分析了相位误差在15°的标准偏差条件下的测向误差，绘制测向精度分布图，分析系统测向精度。

1 阵列测向原理

1.1 非均匀线阵

非均匀线阵是利用电磁波在不同天线阵元之间的波程差与来波方向的关系，进一步求得信号的来波方向，一般来说，辐射源到天线阵列的距离和信号波长相比足够长，因此可以将信号电磁波看作平行波入射。非均匀线阵天线阵元之间距离位置设置十分灵活，在实际应用时更为方便［8］，因此，在现实中的测向系统中，通常适用于安装平台受限或者应用较窄频段范围的情况。非均匀线阵天线模型如图1 所示。

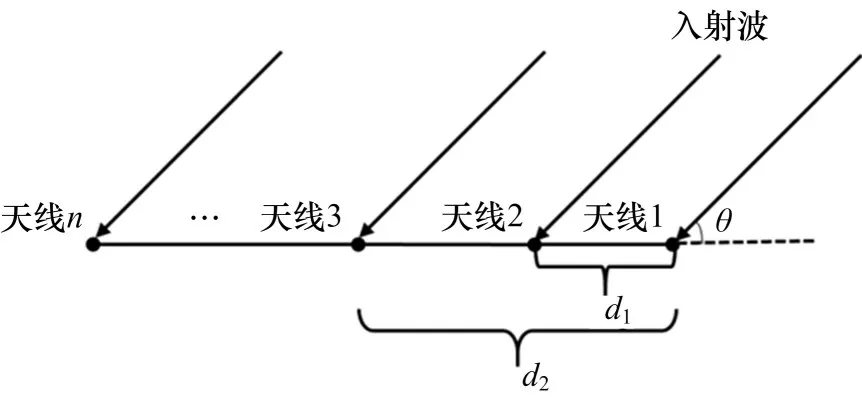
图1 非均匀线阵模型

图1中n为天线阵元个数，d1、d2等分别为其余天线阵元与天线1 之间的间距，θ为入射波方位角。

通过理论模型计算各天线阵元之间相位差，首先可求得天线2 和天线1 之间的相位差为：

进一步可得天线n与天线1 之间的相位差为：

由上面的计算方法可以得到一组各天线与天线1之间的相位差样本库，即顶点基线。由上述公式可灵活变换得到任意2 根天线阵元之间相位差，即：

对式（3）变换求取θ得：

1.2 均匀圆阵

均匀圆阵测向天线阵列模型如图2 所示。

图2 均匀圆阵模型图

图2中n为天线阵元个数，r为天线阵元半径，α为相邻阵元夹角，θ为入射波角度。

均匀圆阵模型构建后，可以通过不同阵元之间相位差计算入射波的到达方向，通过计算阵元与参考圆心点之间的相位差，再通过数学计算可得到不同阵元之间的相位差。首先计算出入射波到达第n个阵元和圆心之间的波程差为：进一步可得到天线n相对于圆心的相位差为：

式中，λ为信号的波长。

通过数学关系可以求得第n个阵元与第m个阵元之间的相位差为：均匀圆阵常用的测向方法有相关法和最小二乘法，相关法的基本原理是：构建无测量误差的理论相位差样本库，将实测相位差矢量在样本库中进行相关查找，具有最大相关系数的矢量对应角度即视为入射波的到达方向［9］。

2 基线选择和相位解模糊

2.1 基线分布

阵列基线是指天线阵元之间组成的连线，一个阵列之中存在多条基线，在使用时根据需要可灵活选择。对于非均匀线性阵列来说，基线情况可以直观看出，只要获取了各天线之间的距离即可计算得出基线长度。以非均匀五元线阵为例，基线示意图如图3所示。

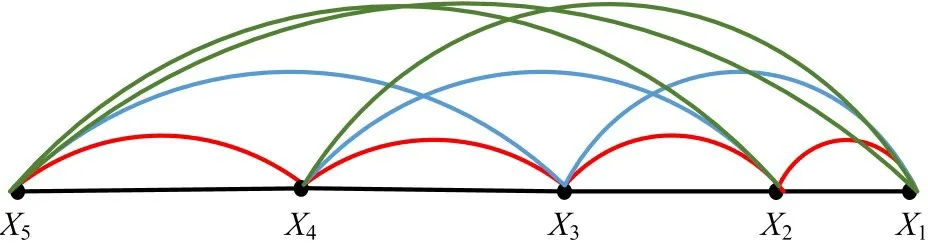
图3 非均匀线阵基线示意图

短基线组合由X1X2、X2X3、X3X4、X4X5和X5X1组成，顶点基线组合有X1X2、X1X3、X1X4、X1X5组成，此外还存在一些基线全部列入全基线组合中，包括X1X2、X2X3、X3X4、X4X5、X5X1、X1X3、X1X4、X2X4、X2X5、X3X5。

以均匀五元圆阵为例，基线示意图如图4 所示。

图4 均匀圆阵基线示意图

短基线组合包括A1A2、A2A3、A3A4、A4A5、A5A1，长基线组合包括A1A3、A2A4、A3A5、A4A1、A5A2以及全基线组合A1A2、A2A3、A3A4、A4A5、A5A1、A1A3、A2A4、A3A5、A4A1、A5A2。

2.2 解相位模糊

由式（1）可知，为求得唯一方位角，需满足φ和θ一一对应，则有：

当不满足该条件时，待测相位差不是真实相位差，与之相差了若干个周期2π，即相位模糊。则解相位模糊就是计算出相差的周期数将其还原为真实相位差，基本流程如图5 所示。

图5 解模糊流程图

解算时，需要以1 根长度小于半波长的基线为基准，其对应相位差无相位模糊。线阵中所有基线均平行，以2 根同向基线为例，如X1X2和X2X3，长度分别为d1和d2，对应相位差分别为φ1和φ2， 假设d1＜λ2、d2＞λ2，则有：

式中，k=0，±1，±2…。对式（9）求解可得：

式中，[·]Z为取整操作。求得k值后代入上式求得相位差φ͂2，以此求得方位角。

实际应用时，得到的相位差包含一定的测量误差，根据式（10）计算出的k值实际是：

式中，△φ1、△φ2为测量误差。当|△k|小于0.5 时，测量误差不影响解相位模糊，通过统计分析可得，当d2d1越小时，解模糊成功率越高，因此，可以利用不同基线组合逐次解相位模糊，提高解相位模糊概率。

假设所有基线均大于半波长，如基线X3X4、X4X5，对应相位差分别为φ1和φ2，长度分别为d1=n1d0和

d2=n2d0，且d0λ＜1 2，此时有：

通过d1和d2合成短基线，有：

式中，t1，t2∈Z，且满足t1n1+t2n2=1。

另式（13）可变换为：

联立式（13）、（14）有：

对均匀五元圆阵来说，获取5 组长基线和5 组短基线后，若是短基线长度小于半波长，则不存在模糊情况，通过基线比获得长基线真实相位差，进而求取方位角；若是短基线长度仍然大于半波长，则需构造虚拟基线进行解模糊。选取同一方向上的2 根长基线和短基线（如A1A4和A2A3），对应相位差分别为φ1和φ2，长度分别为d1和d2，且有d1d2=2cos36°=(3+由于圆阵同向性，采用平行基线法可解相位模糊，通过d1和d2合成虚拟基线d3和d4，采取操作为：

进一步有：

同样地：

另有：

可得出d3和d4对应相位差为：

为使式（20）有唯一解，对其变换可得：

存在唯一解，因此利用基线d1和d2可以对基线正对方位角±90°范围内的相位解模糊，进一步利用5 组长基线和短基线可以对全方位相位解模糊，在满足的条件下，可适当增大基线长度，以提高测向精度。

3 仿真研究

首先，根据输入参数包括尺寸、类型、频率范围等，构建不同的天线模型。其次，在一定的频率范围内，以一定的频率步进和角度步进构建相位差样本库，其中包含每个方位角对应的相位差矢量数据，每个矢量包含阵列中全部基线对应相位差。进行精度仿真测试时，以样本库中的每个相位差矢量为导向矢量，为其增加均方根误差固定的相位误差，并将其归一化到±π 内作为待测相位差，经过解模糊后将其与样本库中理论数据进行相关运算，并求其结果误差。重复以上步骤进行100 次测试，最后求其均方根差作为最终结果，具体流程如图6 所示。

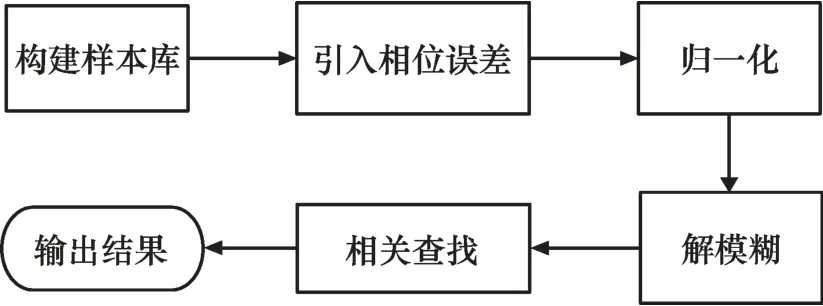
图6 相关法测试流程

3.1 非均匀线阵

以非均匀五元线阵为例，相邻阵元间距长度分别为29 cm、42 cm、71 cm、97 cm，仿真分析不同基线组合对解算结果误差的影响。具体地，分别以短基线组合、长基线组合和全基线组合进行逐次解相位模糊，再进行方位角解算。

短基线组合测向精度结果如图7 所示。

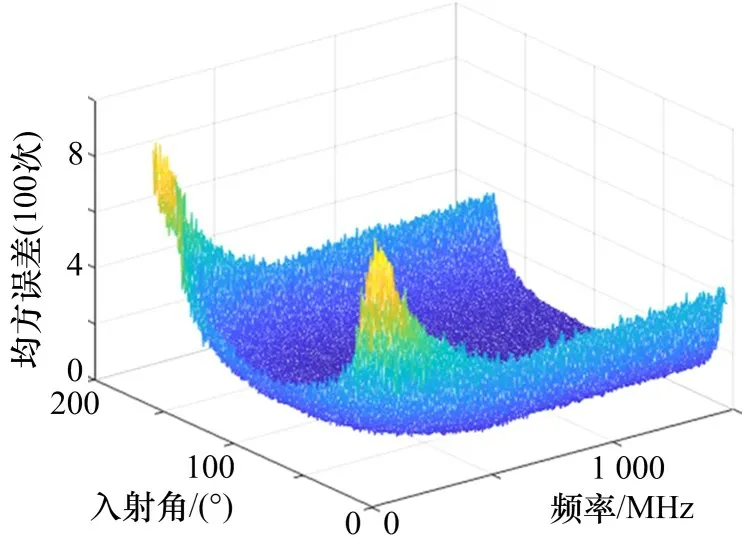
图7 线阵短基线测向精度图

由图7 可看出，随着频率增大，测向精度逐渐减小，并且从线阵法线位置入射来波计算误差最小，从线阵水平方向入射来波计算误差较大，进一步得到在测试条件下，最大测向精度为φ短m=8.794°，法线入射方位最大测向精度为φ法m=2.341°，可用方位角范围在法线±60°范围内。

顶点基线组合测向精度结果如图8 所示。

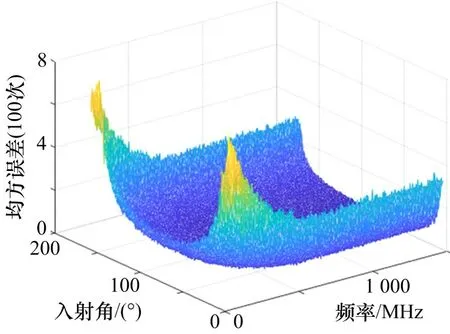
图8 线阵顶点基线测向精度图

图8中最大测向精度为φ短m=7.496°，法线入射方位最大测向精度为φ法m=2.094°，整体趋势与短基线组合相似，整体误差要小于短基线组合。

全基线组合测向精度结果如图9 所示。

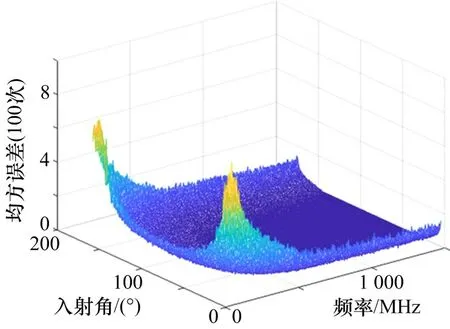
图9 线阵全基线测向精度图

图9中最大测向精度为φ短m=8.051°，法线入射方位最大测向精度为φ法m=2.243°，全基线与顶点基线误差结果相近，均小于短基线误差结果。

由仿真结果可看出，全基线测量精度随着频率的增大而逐渐降低，对基线相位差进行解模糊时，选取不同的基线组合会影响最后的计算结果，全基线和顶点基线的计算误差相近，短基线误差高于全基线和顶点基线。

3.2 均匀圆阵

构建样本库时，频率步进为5 MHz，其将产生最大为2.5 MHz 的测频误差，由式（6）对f求导可得：

当△f取2.5 MHz 时，分别计算全方位角范围短基线组合和长基线组合对应误差，通过某软件变量空间查询可得最大测频误差分别为ψ短=2.116 0°、ψ长=3.423 8°。

当角度步进为1°时，其将产生最大为0.5°的测角误差，由式（6）对θ求导可得：

以f和θ为变量，取△θ为0.5°，计算对应测角误差，如图10 所示。

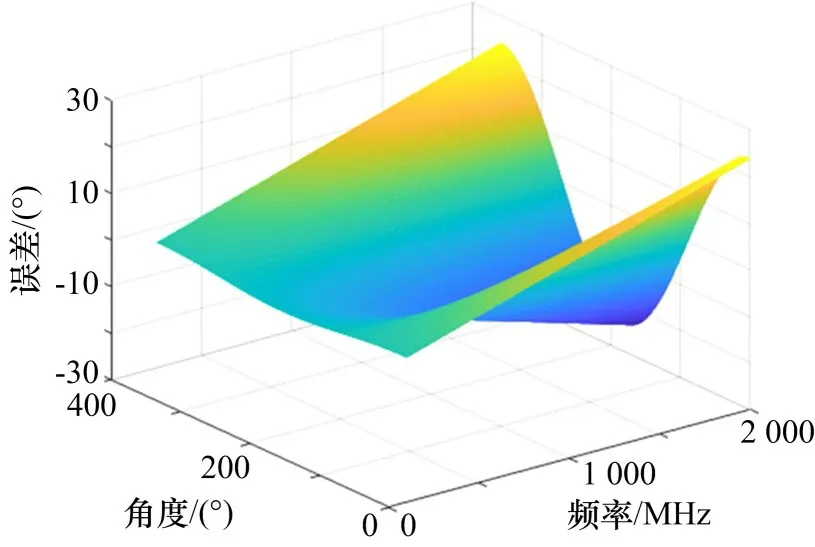
图10 测角误差示意图

由图10 可看出，在频率一定时，误差随方位角增大呈现正弦性变化；在方位角一定时，误差随频率增大呈现线性变化。

给定均匀五元圆阵半径为50 cm，频率步进为5 MHz，角度步进为1°，相位误差均方根误差为15°，将相位差数据引入相位误差后，依据上述方法进行解模糊，获取每个基线对应的真实相位差数据，再将其与样本库中对应相位差通过相关运算求取方位角，与真实方位角对比得到测量误差值。在本文研究中，短基线组合与长基线组合通过相关运算得到方位角精度，分别对其进行仿真分析，结果如图11 所示。

图11（a）为短基线组合测量精度，最大测量精度为ψmax=3.619°，随着频率增大，整体精度随之降低，由于测角误差已经超过引入的相位误差，以最大测角误差作为当时频点的引入误差，频率超过阈值范围后计算误差会逐渐变大。图11（b）中长基线最大测量精度为ψmax=2.704°，整体趋势和短基线解算结果相似，整体误差要小于短基线组合。

由仿真结果可以看出，圆阵利用短基线或者虚拟基线进行解模糊，再选择基线组合进行相关运算，长基线测量精度要优于短基线解算，频率逐渐增大时，测量误差逐渐变小，但随着测角误差的增大，测量精度逐渐变差。

图11 圆阵测量精度分布图

4 结束语

本文首先介绍了以非均匀线阵和均匀圆阵为阵列天线的方位角解算方法，然后阐述了阵列基线的构成，详细分析了以平行基线解相位模糊的原理，并对不同阵列测向精度进行仿真分析，绘制了测向精度分布图。仿真结果表明，非均匀线阵采用全基线组合和顶点基线组合测量精度相近，均高于短基线组合；均匀圆阵测量精度随着频率增大而逐渐降低，使用短基线组合测量精度低于长基线组合测量精度。本文的仿真方法，可为天线设计和工程应用时分析测向误差提供参考。■