基于差分进化算法的微电网小水电PID参数优化研究

汪若涵，庄原，朱艺超，和治翔

（1.云南电网有限责任公司昆明供电局，云南 昆明 650011；2.云南电网有限责任公司曲靖供电局，云南 曲靖 655100；3.云南电网有限责任公司大理供电局，云南 大理 671000；4.云南电网有限责任公司迪庆供电局，云南 迪庆 674400）

0 前言

随着新型电力系统建设，大量分布式光伏、储能等接入配电网，配电网的能量供给发生巨大的变化，在大电网故障情况下，分布式光伏、储能、小水电组成水、光、储微电网稳定运行，可有效提升配电网的供电可靠性。该类微电网稳定运行需要小水电机组有良好的调节性能。而小水电机组调速系统模型参数的准确性直接影响控制器设计，进而影响微电网内机组动态调节特性和微电网的安全稳定[1]。近年来智能算法在函数优化、参数识别等方面表现出一定的优越性，逐步应用于实际工程中。文献[2]提出一种基于粒子群优化算法的小水电PID 控制器参数优化方法，文献[3]提出一种基于差分进化算法的FMS 中机器与AGV 同时调度方法，但上述方法仅用于理论研究，工程实际应用不足。其中，差分进化（DE）算法在发电机参数识别方面产生了一些工程应用案例，但仿真分析和现场实测高效结合还有待提升。因此，如何基于工程实际构建较好的智能算法优化模型，提升模型适应性是工程建设人员今后需考虑的方向。

1 差分进化算法

1.1 标准差分进化算法

差分进化（DE）算法通过种群内个体间的相互合作与竞争而决定寻优方向，其进化流程与遗传算法非常类似[4]，主要优化步骤如下：

1）初始化种群

在搜索范围内按下式随机产生最初种群。

式中，i=1,2,...；Xi,j(0)为初始种群中的第i个个体，xLi,j为个体的下边界，xUi,j为个体的上边界。

2）变异操作

在此阶段通过差分策略实现个体变异,即随机选取种群中两个不同的个体,将其向量差乘以一个系数后与待变异个体进行向量相加。

3）交叉操作

对于第代种群中的每一个个体与变异个体进行交叉操作，产生新个体。

4）选择操作

使经过变异与交叉操作后的新个体与第t代种群中个体进行竞争，选择适应度值较优的个体进入下一代。当且仅当新个体的适应度值好于第t代种群中个体时，新个体替换第t代种群中个体，从而被选为子代，否则第t代种群中个体被予以保留到下一代。种群中的每个个体均代表待优化PID 参数的一组可能解，种群内进行从父代到子代间的变异、交叉与选择操作，循环直到达到最大迭代次数，此时便可获取整个种群最优个体和其对应的最优适应度值，即最优参数[5]。

1.2 DE算法的改进

DE 算法具有容易实现、收敛速度较快、鲁棒性较强等优点，但在实际工程应用中，存在局部搜索性能弱，迭代次数上升后计算时间较长的缺陷。笔者尝试了对差分进化算法在变异环节和选择环节进行改进。

通常情况下为了增加收敛速度，DE 算法变异环节的缩放因子H设为常数，这使得后代染色体的多样性降低。本文尝试了通过改变DE 算法的评价函数来调节缩放因子H，提高后代的多样性，以下为H因子的自适应调整公式：

其中，H∈[Hmin,Hmax]，K为增益基准值，Oa和Ob为迭代特征值，Hmin和Hmax分别为H的最小值和最大值（本文设置Hmin=0.01，Hmax=2.2，Oa=Ob=4，K=30）。

在选择环节考虑了较差后代进入下一次变异的概率，改进的选择方法如下式所示：

其中，r为(0,1)之间均匀分布的一个随机数；T为当前迭代次数下的温度值；Pchoose(off) 表示off迭代次数下的选择概率；f(ui(off)) 表示off迭代次数下所生成的新解；f(xi(off))表示在off迭代次数下当前染色体的解。

通过实际工程应用发现，改进后的ITAE 评价指标变化区间位于百分数的后两位，对于实际工程应用支撑不足，故本文仅做理论上的探究，标准DE 算法结合合适的仿真模型即可满足工程应用参数优化的需求。

2 基于差分进化算法和仿真优化评价的小水电机组调速器PID参数优化

目前，在电网工程应用中，PID 控制器参数优化主要以人工调整为主，该方法不仅费时，而且不能保证控制器的最佳性能，常用的误差性能指标包括ISE、IAE、ITAE、ISTE 等[6]。

差分进化算法已经广泛应用于函数优化、神经网络训练、模式分类、模糊系统控制以及其他应用领域[7]，本文将使用差分进化算法进行PID 控制器参数的优化设计。通过评价差分进化算法迭代后的适应度函数的数值可判断种群中各个体的优劣，选择性能指标较好的积分时间绝对误差（ITAE）作为适应度函数[8]，以期得到最优的调速系统控制策略。该函数表达式如下：

式中，e(t)为系统误差，此处为机组转速变化相对值误差。

PID 控制器应用广泛（系统结构如图1 所示），在仿真水轮机调速系统模块中的形式如图2 所示。

图1 PID控制器系统结构

图2 小水电机组调速系统PID控制图

其中输出端口是系统误差；kp、ki和kd分别是对系统误差信号及其积分与微分量的加权。PID 控制器的性能取决于、和这3 个参数的合理性[9]。PID 控制器的系统结构图如图2 所示。PID 控制器的优化问题就是确定一组合适的参数kp、ki和kd，使得指标达到最优。

在仿真环境下建立的模型如图3 中，调速系统中的PID 控制器中的微分环节由一个一阶环节近似，输出端频率由仿真软件中的yout1d模块输出，再由所编写的m 文件计算得到优化所需要的ITAE 指标。

图3 对模块进行赋值的界面示意图

利用差分进化算法对PID 控制器的参数进行优化设计[9]时在水轮机及其调速系统模块当中的PID 一栏的参数设置为待定参数。

差分进化算法对PID 参数优化的设计过程如图4 所示。

图4 优化PID的过程示意图

图4 中，应用差分进化算法优化更新种群后，依次赋值给PID 控制器的kp、ki和kd参数，然后运行控制系统的仿真评价模型，得到该组参数对应的性能指标，该性能指标传递到差分进化算法中作为该粒子的适应值，最后判断是否可以退出算法[10-11]。

3 基于差分进化算法的PID参数优化仿真

3.1 仿真边界条件

由于对调速系统参数进行整体优化较为困难，容易陷入局部最优，导致参数寻优过程不理想，因此采用分布优化的方法对两台机组的小网控制参数进行优化，实验总共分为3 步进行，首先对单台机组进行负荷扰动实验，对单台机组调速系统PID 参数进行优化，包括kp、ki、kd、bP，Ef 参数；其次，固定一台机组参数后再优化另一台机组的kp、ki、kd、bP，Ef 参数；最后，固定两台机组的PID 参数；最后，对进入小网模式的频率阈值和延时进行优化。

基于软件进行仿真，迭代次数为100 代。安南电站小水电机组与10 kV 白水台线组成微电网，小水电机组的仿真参数设置情况如下：kp、ki的取值范围为[0,1]，kd取值范围为[0,5]，bP=0。现场小水电站调速系统控制面板参数设置情况如下：T1v 为0.3 s，kp为6，Tw 为1.6s，Ta 为8.2 s，en为1.0，Ky 为0.5。设置4% 的频率扰动。

3.2 小水电机组PID参数优化仿真

仿真结果如图5 所示，可以看出DE 算法的性能指标ITAE 不断减小，PID 控制器的kp、ki、kd参数被不断的优化，逐步向最优逼近。

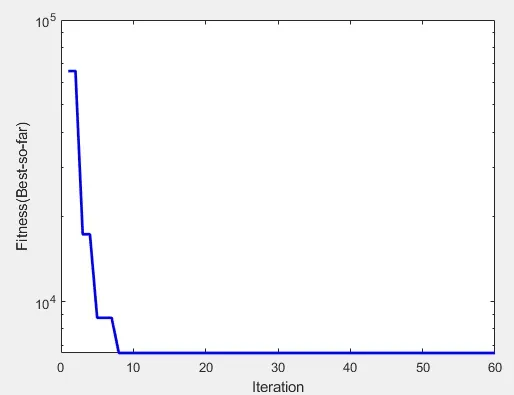
图5 DE算法适应度曲线

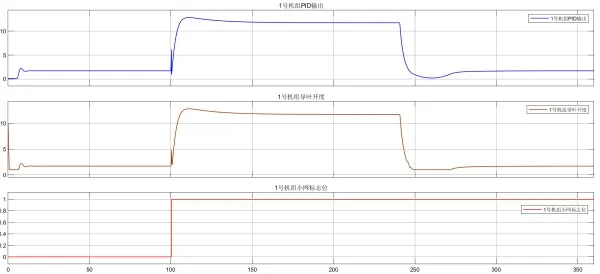
图6 负荷扰动时1号机组调速系统动作曲线（参数优化前）

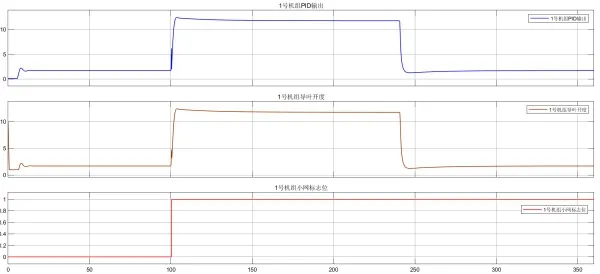
图7 负荷扰动时1号机组调速系统动作曲线（参数优化后）

由上述结果分析得出，在系统侧扰动±300 kW 负荷时，调速系统小网参数优化前，系统最高频率为52.4 Hz，最低频率为47.3 Hz，通过DE 算法优化后，同样在系统侧扰动±300 kW 负荷时，系统最高频率为51.4 Hz，最低频率为48.5 Hz，故DE 算法对于小网模式PID 参数优化具有较好的效果。优化后的1 号机组调速系统小网PID 参数为kp=2.25、kp=0.8、kd=0.4、bP=0，Ef=±0.3 Hz。

3.3 安南电站小水电机组参数的优化

由安南电站、10 kV 白水台线组成微电网运行小水电机组进行参数优化及实验验证。

基于差分进化算法对调速系统小网PID 参数实测、辨识以及优化后，最终得到1、2 号机组调速系统初始化PID 参数配置表（见表1），用于后续仿真模拟和动态验证环节。

表1 调速系统参数初始化配置

3.4 安南电站孤网运行稳态验证

3.4.1 安南电站1，2号机组供白水台及东坝线稳态运行过程

断开011 后1，2 号机组供白水台及东坝线运行过程，最高频率50.55 Hz，最小频率49.35 Hz，满足GB/T 9652.1-2019《水轮机调速系统技术条件》中孤网运行频率不超过±3%的要求。

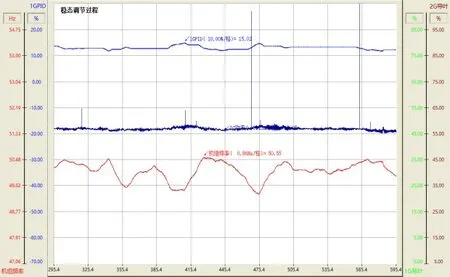
图8 1、2号机组小网模式稳态运行过程（单位 / s）

3.4.2 安南电站1机组供白水台线稳态运行过程

1 号机组供白水台线稳态运行过程，最高频率50.83 Hz，最小频率49.29 Hz（线路负荷有波动情况下），满足GB/T 9652.1-2019《水轮机调速系统技术条件》中孤网运行频率不超过±3%的要求。

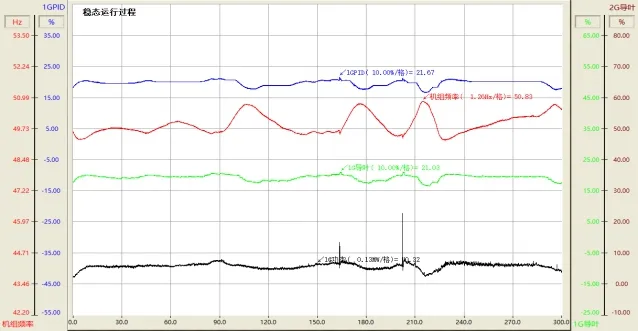
图9 1号机组小网模式稳态调节过程

3.4.3 安南电站1机组与储能系统共同供白水台线、乡政府线、江边哈巴线稳态运行过程

1 号机组与储能、光伏系统供白水台线、乡政府线和江边哈巴线稳态运行，频率波动范围减小（线路负荷有波动情况下），最高频率49.88 Hz，最小频率49.64 Hz（线路负荷有波动情况下）。

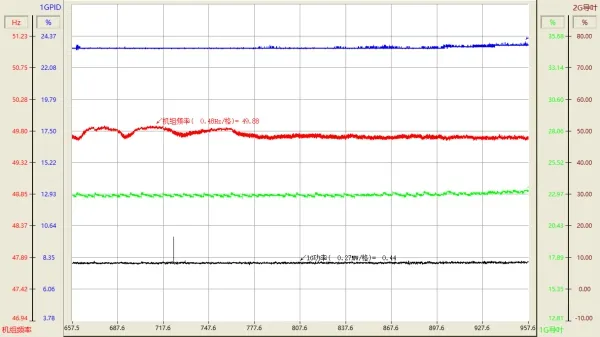
图10 水、光、储小网模式稳态调节过程

安南电站1、2 号机组调速系统导叶开度、PID 输出、功率信号、频率信号、小网动作信号量值，实测信号数据正确且真实有效。

试验分别进行了安南电站1、2 号机组带白水台及东坝线运行、1 号机组带白水台线运行、1 号机组及储能系统带白水台线、乡政府线及江边哈巴线运行，试验过程中的指标均满足相关标准要求，验证了安南电站1、2 号机组调速系统小网模式相关参数配置的合理性，同时也验证了安南电站具备微电网组网能力。

4 结束语

1）通过DE 算法以及小水电机组调速系统仿真评价模型可以有效优化实际机组系统PID参数，使得现场参数辨测次数减少，提升了机组参数优化的效率；

2）实际应用中可把基于ED 算法的小水电机组调速系统PID 参数仿真优化方法和现场实测方法相结合，减少实测次数和范围；

3）繁琐的改进DE 算法并不适合现场工程应用，对参数优化结果支撑性不足，故实际工程应用中不推荐改进的DE 算法，应寻求更合适的智能优化算法，提升优化效率和精度。