1 435 mm与1 000 mm轨距三线套轨铁路道岔的动力学特性
曹庆川 王建西,3 郭庆 王晓曼
1.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室, 石家庄 050043;2.石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室, 石家庄 050043;3.河北省铁路扣件系统技术创新中心, 石家庄 050043
随着经济快速发展,我国同周边国家的交流与商贸互通越来越密切。由于不同国家使用的铁路轨道轨距不尽相同,给铁路运输带来了很多不便。为满足两种不同轨距的车辆通过道岔,可将两组不同轨距的同向单开道岔套合在一起,构成套轨铁路道岔,解决轨距不同的问题。使用套轨铁路道岔能够解决不同国家不同轨距列车的开行问题,使得列车在口岸站以远的线路上能正常行驶,对货物列车不再进行换装作业和换轮作业,减少货车在口岸站的停留时间。
与普通铁路道岔相比,套轨铁路道岔兼具两种不同轨距的轨道。由于套轨铁路道岔为非对称结构,会造成轨道刚度不均匀,使车辆过岔的影响因素更加复杂;套轨铁路道岔尖轨尖端处的结构不平顺及跟端结构会影响列车的振动加速度;固定辙叉尖端处的结构不平顺及其跟端结构会影响横向及竖向稳定性;道岔部件强度、钢轨接头等均会对运行安全性与舒适性有严重影响。因此,研究套轨铁路道岔的动力学特性具有重要意义。
相关学者对车辆-道岔系统的动力学特性进行了研究。任尊松等[1]通过自编程序研究了岔心区心轨关键截面轨顶高度降低值对高速道岔系统动力特性的影响。司道林等[2]分析了高速列车通过道岔区时轮轨相互作用特点,得出道岔区多点接触、滚动圆半径改变等复杂的轮轨接触关系。陈浩等[3]以18号可动心轨道岔为研究对象,运用多体动力学软件UM分析了列车通过道岔时的轮轨力、舒适性指标和安全性指标。李伟等[4]建立了12号道岔的模型,仿真分析车辆过岔时的动力学特性,发现钢轨廓形打磨能够有效改善道岔区的动力学性能。Xin等[5]建立车辆-道岔耦合动力学模型,仿真分析车辆过岔时的动态响应。张利等[6]以货车过岔为例,建立车辆-道岔-有砟道床刚柔耦合模型,发现货车引起的环境振动大于客车,道岔区道床的环境振动大于正线区道床;环境振动随传播距离增加呈衰减趋势;在振动传播过程中不同衰减断面的环境振动主频率为31.5或40.0 Hz。周俊召等[7]基于多体动力学研究了不同曲线线形与超高条件下列车过岔动力学响应。杨逸航等[8]研究了高速铁路道岔受限区钢轨打磨对列车动力学性能的影响。
关于套轨铁路道岔动力学特性的研究较少,且鲜有学者对列车不同速度下套轨铁路道岔的动力学响应进行研究。因此,本文以标准轨普通单开道岔为参考,结合石太铁路现场实测数据,设计一种1 435 mm与1 000 mm轨距三线套轨铁路道岔。由于侧向行驶时宽轨距铁路拥有更好的稳定性,因此采用标准轨距铁路转向、米轨铁路直行的套轨铁路道岔方案。通过建立道岔区轮轨系统空间耦合振动模型,采用道岔动力学理论分析标准轨距货车侧向过岔及米轨货车直向过岔时的各项动力学响应,分析货车以不同速度通过道岔时的动力学响应变化规律,确定货车能够安全通过套轨铁路道岔的安全限值。
1 车辆-道岔耦合动力学模型
1.1 车辆模型
建模时,米轨货车按照中国出口马来西亚的类型考虑,标准轨距货车参照我国铁路目前正在使用的主型货车,车辆参数参见文献[9]。建立整车模型,车体、转向架及轮对主要考虑横摆、浮沉、侧滚、点头和摇头振动,共50个自由度。
中国出口马来西亚的米轨货车为SDD12型内燃车,最大运营速度100 km/h,考虑到车辆运行安全,取持续运营速度90 km/h。标准轨距货车采用C80型货车,设计要求侧向过岔速度达到50 km/h。直向过岔速度主要受辙叉有害空间的制约。如60 km/h钢轨、AT弹性可弯尖轨和高锰钢整铸辙叉的12号道岔,因存在有害空间,允许直向过岔速度为120 km/h。侧向过岔速度主要受侧向导曲线半径大小的制约,半径愈大,允许通过速度愈大。如12号提速道岔的导曲线半径为350 m,允许侧向过岔速度为50 km/h。道岔号码越大,过岔速度越大。因此,直向过岔速度取90 km/h,侧向过岔速度取50 km/h。根据所选车辆,货车通过轨距1 000 mm道岔时,车辆轴重取10 t;通过轨距1 435 mm道岔时,车辆轴重取25 t。
1.2 套轨铁路道岔模型
建立套轨铁路道岔仿真模型,主要是建立道岔的线形和变截面轨道模型。道岔线形参数主要包括道岔的导曲线半径、前长、后长、全长等。由于道岔区钢轨是变截面钢轨,建立套轨铁路道岔三维模型,并生成关键截面进行线性插值处理,得到道岔全部变截面特征。1 435 mm与1 000 mm轨距三线套轨铁路道岔平面见图1。区间轨道的横截面没有变化,而道岔区轨道需要考虑单侧钢轨的变截面特性,将轨道看作变截面梁[10]。道岔全长为29.49 m。辙叉选用60 kg/m固定式辙叉,采用半切线型导曲线,半径为350 m。尖轨为半切线曲线尖轨,尖轨尖端为藏尖式,曲线尖轨长7.402 m,曲线尖轨最小轮缘槽宽度为62.33 mm。道岔区存在几何不平顺,采用美国五级轨道谱。
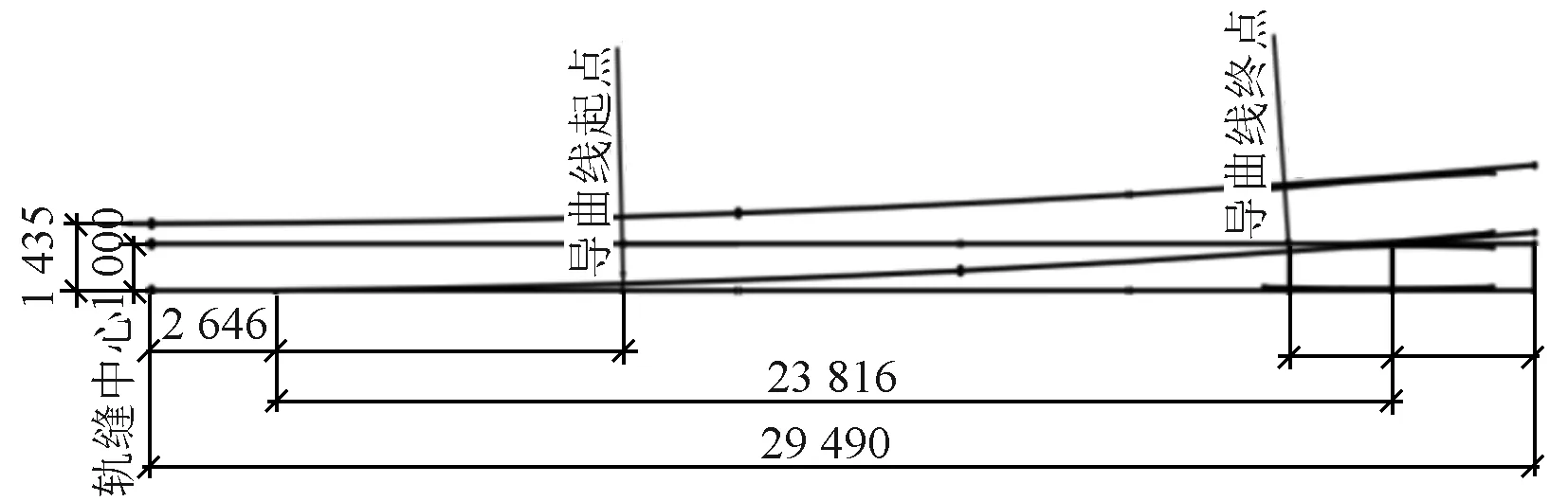
图1 1 435 mm与1 000 mm轨距三线套轨铁路道岔平面(单位:mm)
与普通铁路道岔相比,本文设计的套轨铁路道岔主要结构特点如下:①道岔结构构造上不再使用直线尖轨、整铸式直线辙叉的组合形式;②仅在侧股的标准轨距铁路线路的右股上存在一根尖轨,在左股上没有直线尖轨;③尖轨长7.402 m,大于标准轨12号普通单开道岔尖轨长度;④辙叉角为4°49'45″,与12号道岔相同。
1.3 动力学评价指标
根据重载铁路道岔的试验和运营经验,选取的车辆-道岔动力学性能评价指标见表1。

表1 动力学性能评价指标
2 动力学仿真分析
对货车以50 km/h侧向通过标准轨距铁路道岔和90 km/h直向通过米轨铁路道岔的动力学响应进行分析。其中,100 ~ 105 m为转辙器区,105 ~ 124 m为连接部分,124 ~ 128 m为辙叉区。为使套轨铁路道岔分离,减小过岔难度,分析货车侧向过岔工况时只考虑通过标准轨距铁路道岔模型,分析货车直向过岔工况时只考虑通过米轨铁路道岔模型。货车侧向通过标准轨距铁路道岔和直向通过米轨铁路道岔时的脱轨系数、轮重减载率分别见图2、图3。
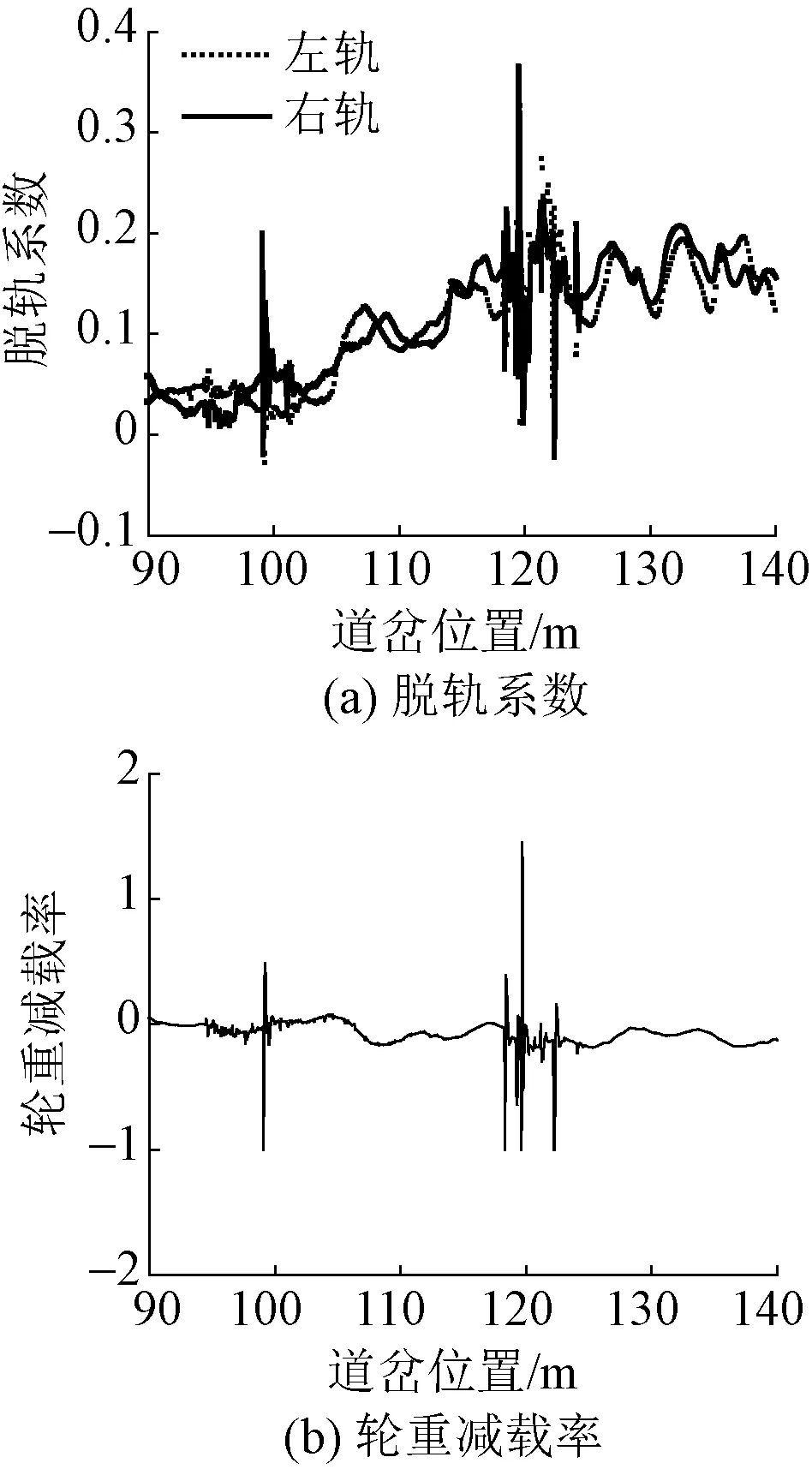
图2 货车侧向过岔时的安全性指标
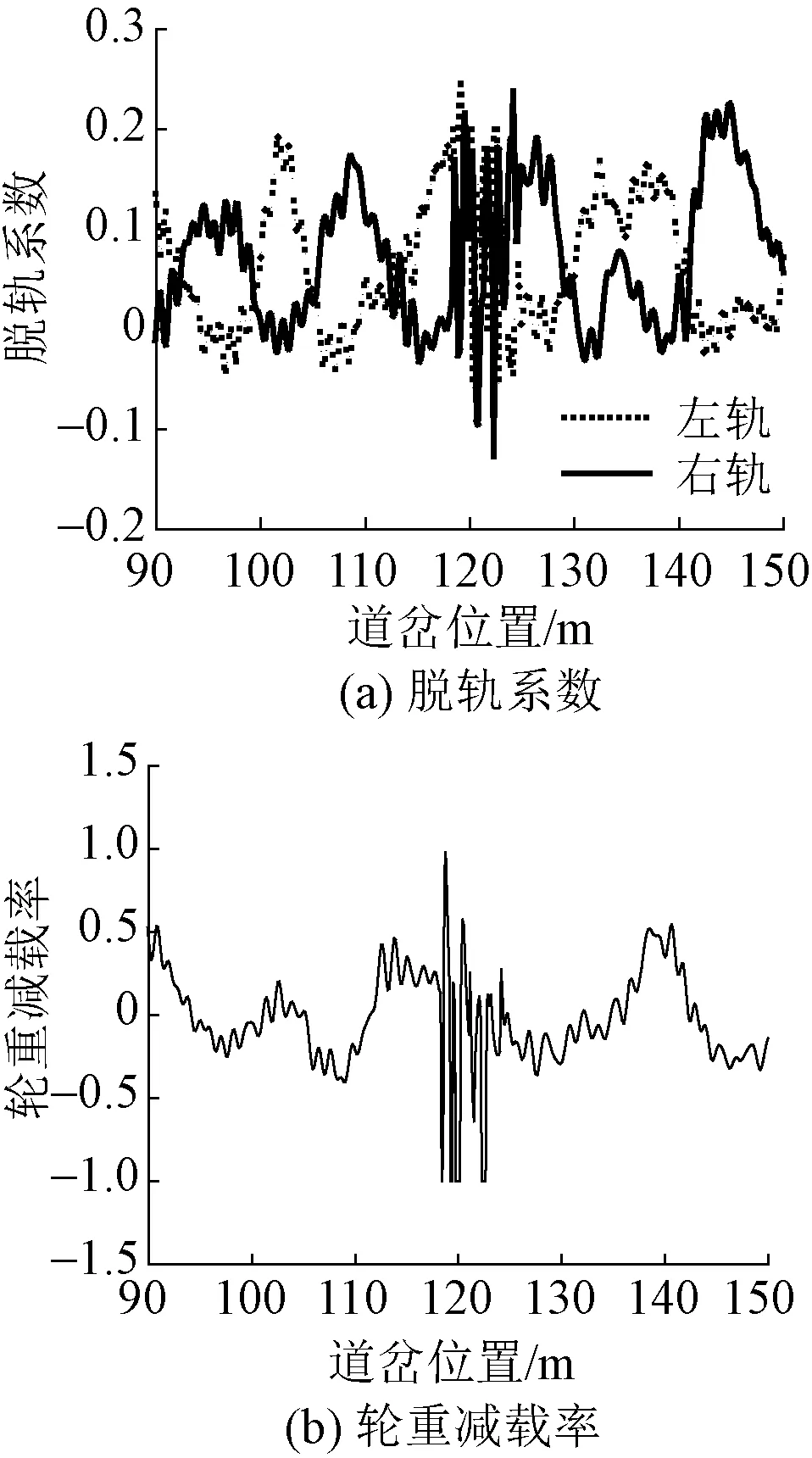
图3 货车直向过岔时的安全性指标
由图2可知:货车侧向通过转辙器区时,车轮的脱轨系数最大为0.13,这是由轮对与尖轨之间的接触冲击引起的;车轮轮载由基本轨过渡到尖轨时,轮轨系统存在多点接触,故轮重减载率在转辙器区产生峰值,为0.11;货车通过导曲线时,最大脱轨系数为0.15,最大轮重减载率为0.18;在辙叉区,轮轨接触冲击和轮载的转移过渡引起安全性指标增大,最大脱轨系数为0.36,最大轮重减载率为1.00,脱轨系数处于安全范围以内,轮重减载率超过安全限值,这是因为在经过辙叉时,车轮在有害空间出现了短暂悬空状态[2]。货车侧向过岔时,脱轨系数在0.08 ~ 0.32,轮重减载率在0.06 ~ 0.62(不考虑瞬间悬空状态),与相同转辙角实测客货共线12号道岔数据相比[4],货车在侧向通过套轨铁路道岔的标准轨距铁路区段时安全性更高。
由图3可知:货车直向过岔时,在辙叉处安全性指标较大,最大脱轨系数为0.25,最大轮重减载率为1.0,轮重减载率在瞬间超过了安全限值,这是因为在经过辙叉时车轮在有害空间出现了短暂悬空状态。货车直向过岔时,脱轨系数在0.04 ~ 0.25,轮重减载率在0.06 ~ 0.46(不考虑瞬间悬空状态),与相同转辙角实测12号道岔数据相比[4],货车在直向通过套轨铁路道岔的米轨铁路区段时安全性更高。
对于1 435 mm与1 000 mm轨距三线套轨铁路道岔,货车侧向过岔与直向过岔时动力学响应最大值见表2。
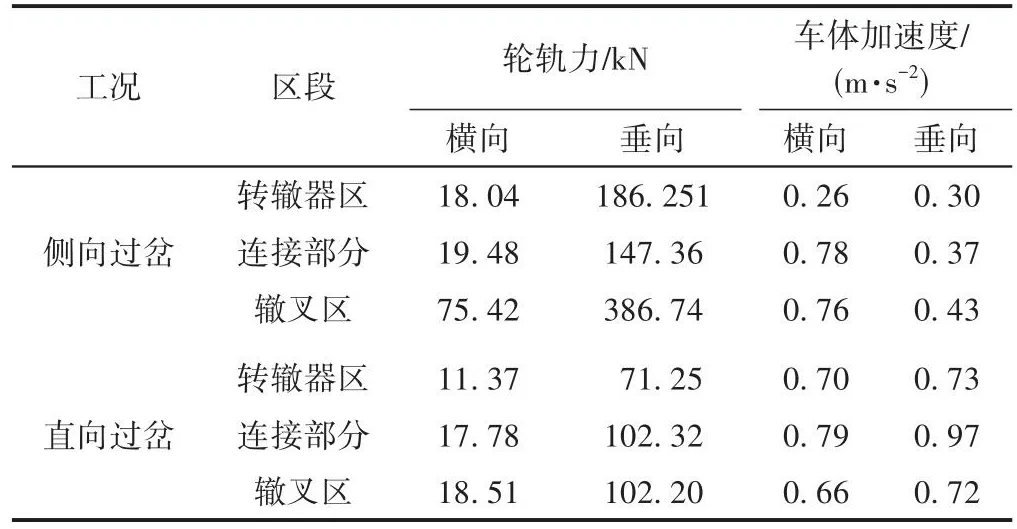
表2 货车侧向过岔与直向过岔时动力学响应最大值
由表2可知:①货车以50 km/h侧向通过标准轨距铁路道岔时,其轮轨横向力与轮轨垂向力最大值均出现在辙叉区,轮轨横向力最大值为75.42 kN,轮轨垂向力最大值为386.74 kN;车体横向加速度最大值出现在连接部分,车体垂向加速度最大值出现在辙叉区,车体横向加速度最大值为0.76 m/s2,车体垂向加速度最大值为0.43 m/s2。②货车以90 km/h直向通过米轨铁路道岔时,车体横向加速度最大值出现在连接部分,其轮轨横向力、轮轨垂向力、车体垂向加速度最大值均出现在辙叉区。轮轨横向、垂向力最大值分别为71.25、102.32 kN,车体横向、垂向加速度最大值分别为0.73、0.71 m/s2。
与文献[10]进行对比发现,本文仿真结果在波形和峰值上都较为接近,验证了所建立模型的准确性。
3 过岔速度
对货车以不同速度通过1 435 mm与1 000 mm轨距三线套轨铁路道岔的动力学特性进行分析。货车侧向过岔工况下,分别提取速度30 ~ 70 km/h时道岔的转辙器区、连接部分、辙叉区动力学指标的最大值;货车直向过岔工况下,分别提取速度70 ~ 100 km/h时道岔的转辙器区、连接部分、辙叉区动力学指标最大值。由于在以50 km/h侧向过岔和以90 km/h直向过岔时轮轨力与脱轨系数的最大值均出现在右轮,因此研究时取不同速度下第一轮对右侧车轮动力学响应进行分析。
3.1 过岔速度对轮轨作用力的影响
货车以不同速度过岔时,转辙器区、连接部分、辙叉区轮轨力变化曲线见图4、图5。

图4 不同速度下货车侧向过岔时的轮轨力变化曲线
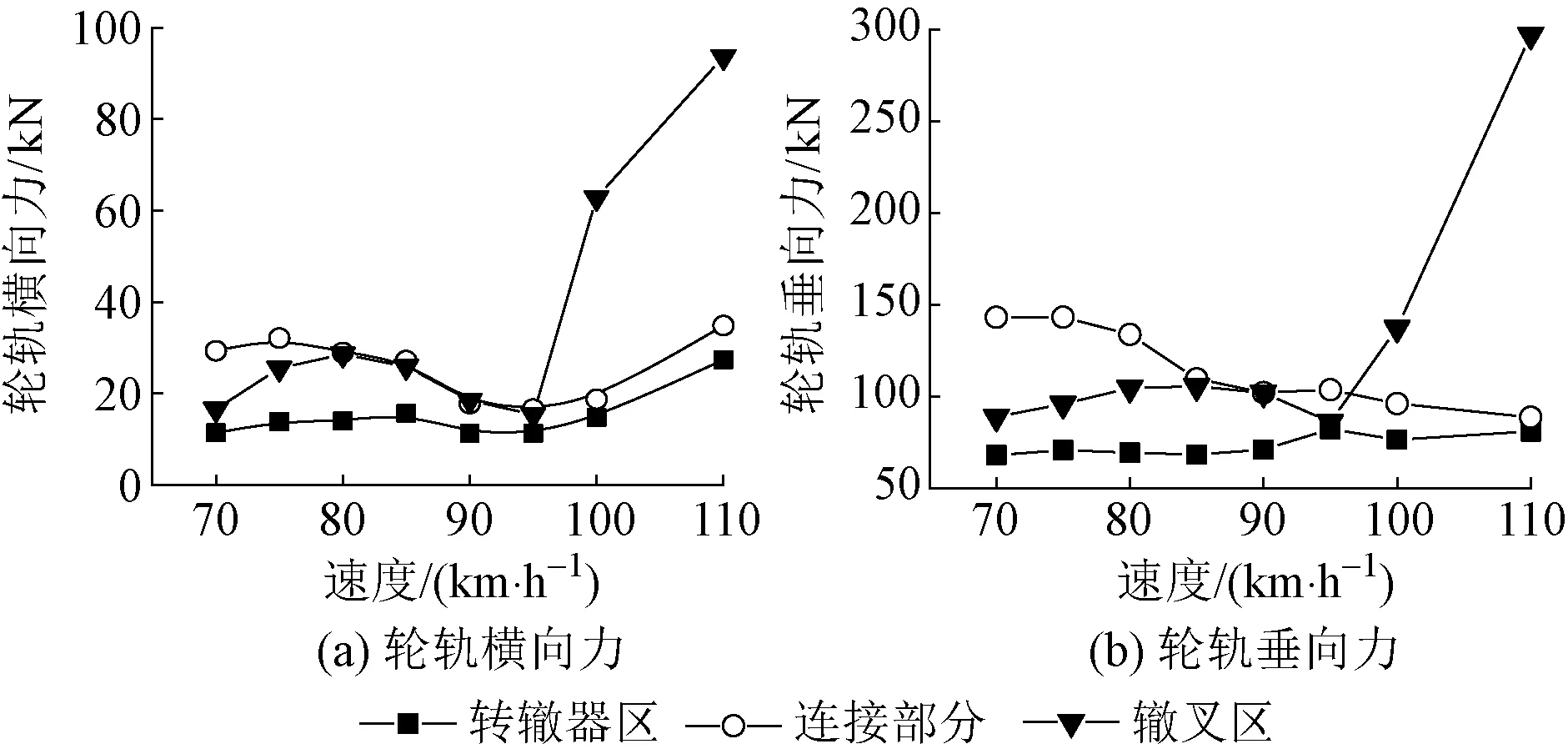
图5 不同速度下货车直向过岔时的轮轨力变化曲线
由图4可知:
1)货车侧向通过标准轨距铁路道岔时,轮轨横向力和垂向力的最大值均出现在辙叉区;随着运行速度提高,轮轨横向力有降低趋势。这是因为速度较低时,其振动频率也相对较低,可能会与悬挂固有频率耦合,货车和轮对发生耦合振动,进而导致轮轨横向力偏大。随着速度增大,轮对的运动频率会逐渐高于货车悬挂系统的固有频率,耦合程度降低,导致轮对稳定性增强[11]。
2)货车速度小于50 km/h时,辙叉区轮轨垂向力随着速度增加而增大,速度超过50 km/h后呈波动状态。这是因为在侧向通过套轨铁路道岔辙叉区时,右轮轮背与护轨产生冲击,诱发了轮对的振荡。当车体垂向一阶弯曲频率与车体点头振动空响应点频率接近时,会发生车体的垂向弹性共振。随着运行速度的提高,弹性车体垂向会出现波动[12]。同时,由于货车载重较大,在经过辙叉咽喉时,货车前后轮对依次出现瞬间悬空状态,随着速度增大,轮对点头运动出现波动变化,导致轮轨垂向力波动。速度为50 km/h时,轮轨横向、垂向力均最大,分别为75.42、386.74 kN,但均在安全限值以内。
由图5可知:货车以不同速度通过米轨铁路道岔,速度小于90 km/h时,轮轨横向力和轮轨垂向力的最大值出现在连接部分;当过岔速度超过90 km/h后,轮轨横向力和轮轨垂向力的最大值出现在辙叉区。这是因为在辙叉区钢轨截面廓形发生变化,存在固有不平顺,且由于固定式辙叉存在有害空间与叉心,货车在以较高速度通过时会产生较大的轮轨冲击。轮轨横向力和轮轨垂向力均在安全限值以内。因此,在货车直向通过米轨铁路道岔时,可以适当增大过岔速度,但不能超过105 km/h。
3.2 过岔速度对货车系统振动特性的影响
货车以不同速度过岔时,转辙器区、连接部分、辙叉区车体振动加速度变化曲线见图6、图7。
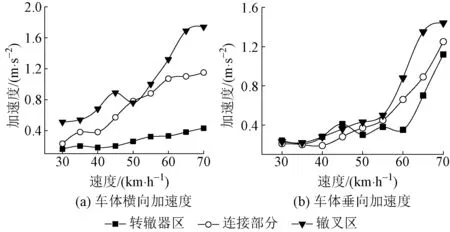
图6 不同速度下货车侧向过岔时车体振动加速度变化曲线

图7 不同速度下货车直向过岔时车体振动加速度变化曲线
由图6可知:货车以不同速度侧向通过标准轨距铁路道岔时,车体横向、垂向加速度在道岔的转辙器区、连接部分、辙叉区均呈逐渐增大的趋势,最大值均出现在辙叉区。速度达到65 km/h时,车体横向加速度为1.69 m/s2,超过了安全限值。
由图7可知:货车以不同速度直向通过米轨铁路道岔时,车体横向、垂向加速度的最大值均出现在连接部分,且随着货车速度增加而呈现波动增大。这是由于货车在经过曲线区段时,轮轨接触状态为多点接触,轮轨接触复杂多变。直向通过速度达到105 km/h时,车体横向、垂向加速度分别为1.62、2.14 m/s2,超过了安全限值。
3.3 过岔速度对安全性指标的影响
货车以不同速度过岔时,转辙器区、连接部分、辙叉区脱轨系数和轮重减载率变化曲线见图8、图9。
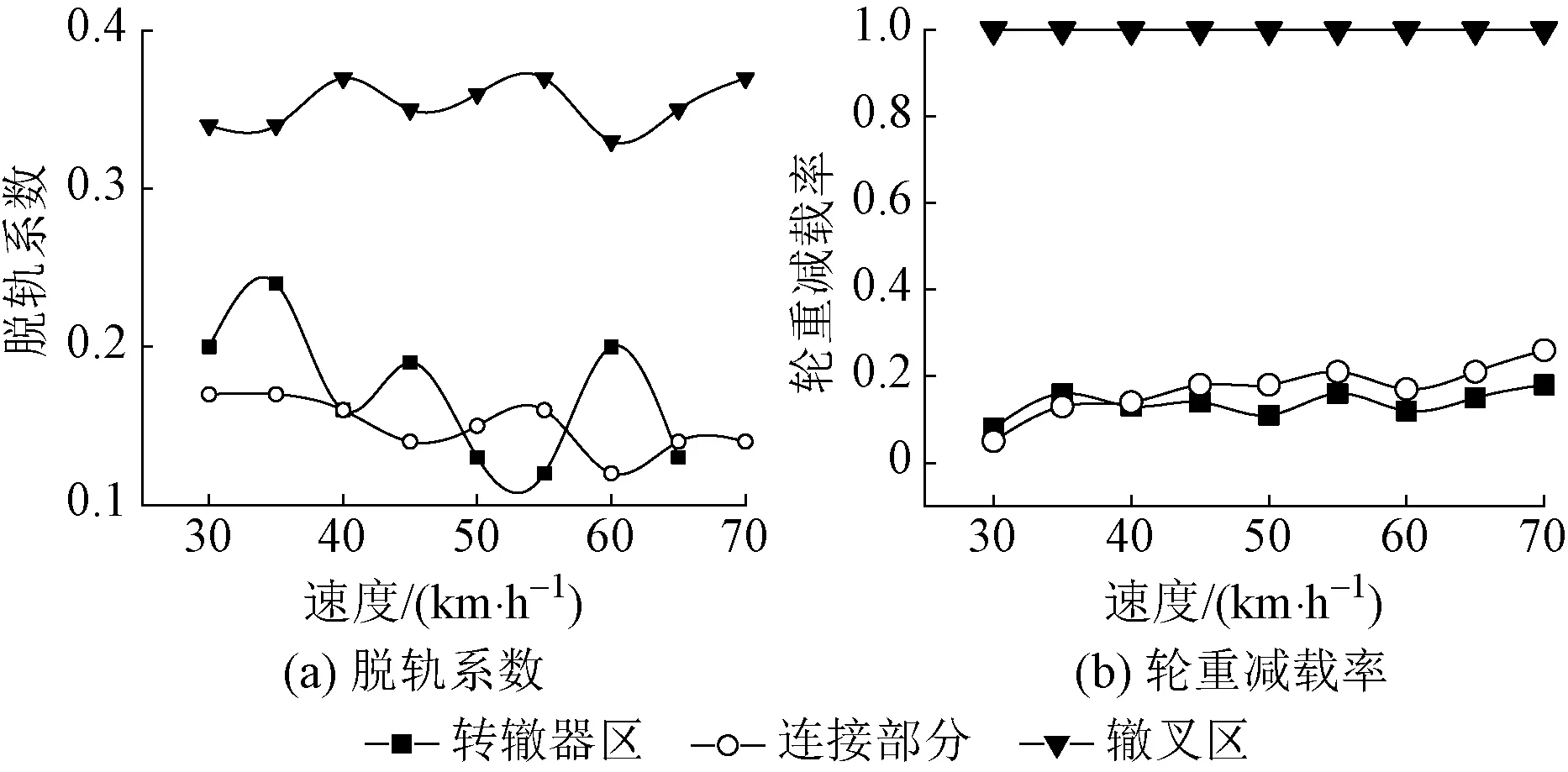
图8 不同速度下货车侧向过岔时安全性指标变化曲线
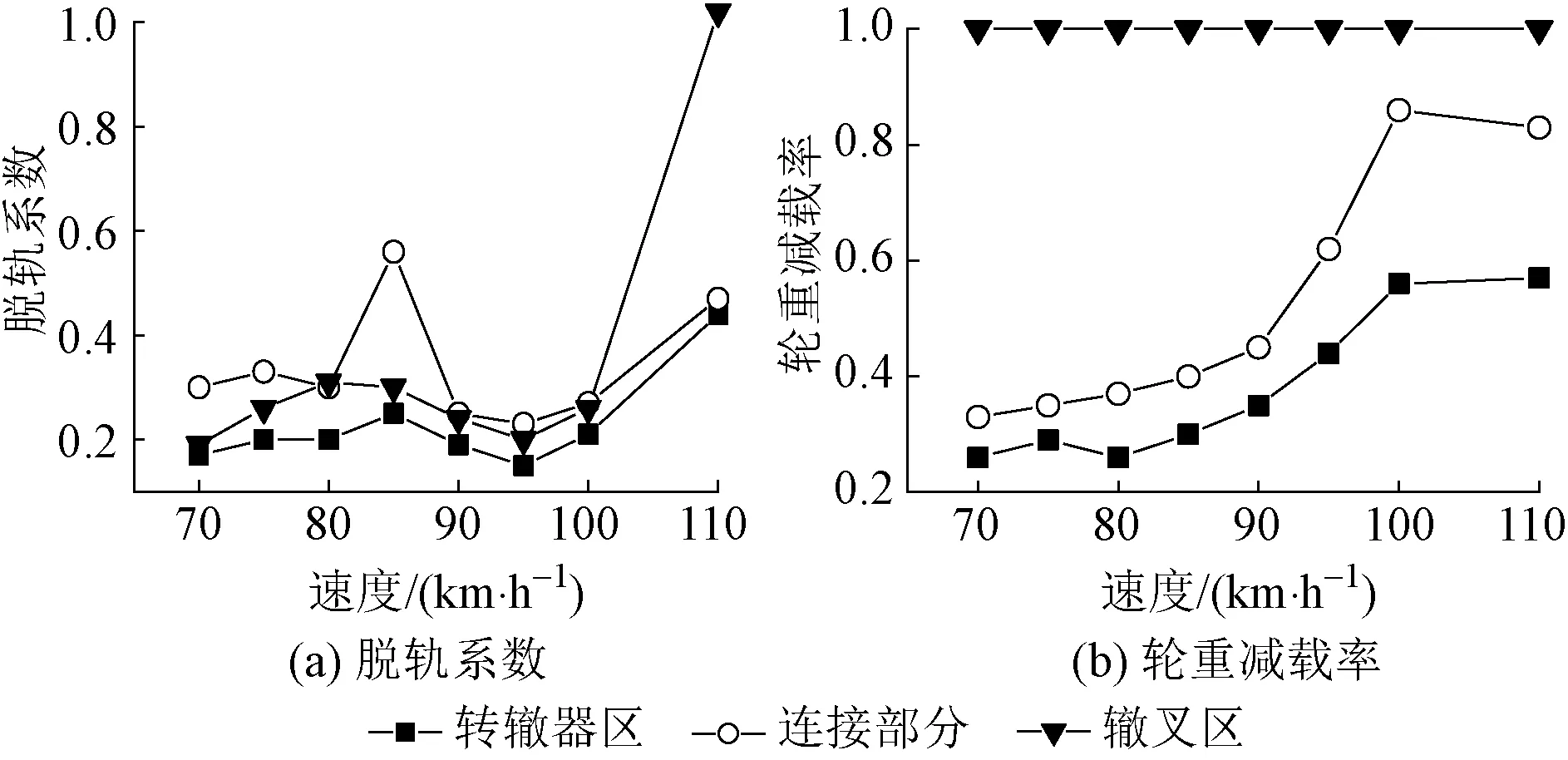
图9 不同速度下货车直向过岔时安全性指标变化曲线
由图8可知:货车侧向通过标准轨距铁路道岔时,脱轨系数与轮重减载率均呈现波动状态,但波动幅度不大。脱轨系数受过岔速度的影响相对较小。安全性指标的最大值均出现在辙叉区,其中,脱轨系数最大值为0.37,未超过安全限值;轮重减载率最大值均为1.00。这是由于辙叉区存在有害空间,车轮在经过有害空间时处于瞬间悬空状态,导致轮重减载率偏大。
由图9可知:货车直向通过米轨铁路道岔时,脱轨系数最大值出现在轨道连接部分,且随着速度增大而增大;轮重减载率在转辙器区、连接部分、辙叉区均呈增大趋势,且最大值出现在辙叉区。速度为110 km/h时,脱轨系数为1.12,超过了安全限值。因此,货车直向通过速度应小于110 km/h。
综上,货车侧向过岔时,速度不应超过65 km/h;货车直向过岔时,可以适当提高过岔速度,但不应超过105 km/h。
4 结论
1)货车侧向通过标准轨距铁路道岔时,轮轨横向力、轮轨垂向力、脱轨系数、轮重减载率、车体垂向加速度最大值出现在转辙区,车体横向加速度最大值出现在连接部分;货车直向通过米轨铁路道岔时,各项安全评价指标的最大值均出现在辙叉区。
2)过岔速度会对货车通过套轨铁路道岔的动力学响应产生影响。货车在以不同速度侧向通过标准轨距铁路道岔和直向通过米轨铁路道岔时,其轮轨力、振动加速度、脱轨系数及轮重减载率并非随着速度增大而单调递增,而是呈现波动状态。
3)货车侧向通过标准轨距铁路道岔,行车速度在45 ~ 70 km/h时,轮轨力、脱轨系数会存在较大波动;货车直向通过米轨铁路道岔时,速度超过95 km/h后动力学响应明显增大。
4)为使货车能够在满足安全限值的条件下侧向通过标准轨距铁路道岔、直向通过米轨铁路道岔,侧向过岔速度不应高于65 km/h,直向过岔速度不应高于105 km/h。
5)在辙叉区存在有害空间,货车经过辙叉区的变截面轨道时会出现瞬间悬空状态。

