从高考题中探究比较大小的方法
——以2022年新高考Ⅰ卷第7题为例
周福运
(南京体育学院附属学校,江苏 南京 210014)
比较大小是高考中常考常新的一类问题,近几年常以选择题压轴题呈现.这类问题往往将指、对、幂形数等混在一起,进行排序.通常具有题干简洁,立意新、角度新、解法灵活多样等特点,能多方面多角度考查考生分析问题、解决问题的能力.
1 试题再现
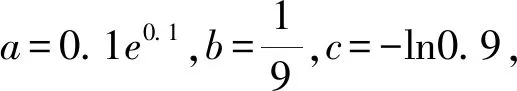
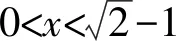
A.a 分析比较大小一直是一个热门的考查形式.因为条件简单,只需要三个数字,但是能很好地考查考生对于函数和不等式的理解.处理这类型问题的方法有:单调性法、作差(商)法、中间值法等.但对于不同类型(如指数、对数、三角函数)且数值大小差距较小并且数值也较小的比较,常规的方法就不能很好地解决了.因此我们需要寻求一些其他方法来解决这类问题,比如构造函数、放缩、泰勒展开等. 纯数字比大小问题一般带有函数背景,需要找寻数字间的关系,利用构造函数解决此类问题是我们常用的方法. 2.1.1比较a,b的大小 则u3(x)在x∈(0,1)上单调递减,u3(x) 评析本解法同思路1的解法.这里的变形仅提取x,剩下的函数求导分析单调性虽然相对较麻烦,需要进行两次求导,但是处理的方法也是通性通法,需要考生掌握,熟练运用导数对函数进行分析. 2.1.2比较b,c的大小 所以u(t)在(0,1)上单调递减. 则u(t)>u(1)=0. 所以当x∈(0,1)时G(x)=g(x)-h(x)>0. 2.1.3比较a,c的大小 解析设H(x)=f(x)-h(x)=xex+ln(1-x)(0 所以a>c. 本题虽然是构造函数的常规处理,但考场上需要三次构造函数,并且需要多次求导,对考生的要求很高.今后备考中,仍需要求学生注重函数解决不等式问题的处理方法,并且在运算过程中注重等价变形,往往变形会得到奇效[1]. 上述构造函数求解时,会发现a,c的大小比较求导一次是不能处理的,需要二次求导,很多同学可能就没有了勇气.而这个问题对于积累了很多经典不等关系的同学来说,可能会简单一些,这里利用一些关于指数对数的经典不等式也可以求解,但这就对同学们的复习质量提出了更高要求. ③ex≥x+1,当x=0时取等; 综上所述,c 评析此解法中对于①④不等式,一般考生不是太熟悉,下面给出简单解释. c 对于不同类型指数、对数、三角函数等的数值,当比较大小差距特别小的数值时,单调性法、中间值等常规的方法就不太够用,通过构造函数一般可以解决,但是技巧性要求相对较高,并且运算量也较大.那么在考生学有余力的情况下,就可以让学生掌握像泰勒展开这种高精度大小的方法.泰勒展开式的作用之一就是估算,通过估算比较相近数的大小.近几年高考题中都有出现比较大小的题目,在人教版和苏教版新教材的三角函数章末习题中都介绍了泰勒展开式,并给出了sinx,cosx的展开式.因此,对于部分考生来说,有必要了解泰勒展开式及其应用. 为了方便记忆,可以把上述公式记为: 常见的麦克劳林展开式: 综上,c 有没有不需要记忆泰勒展开公式的估算方法可以解决此题呢?由此,我们对三个数值的大小比较进行适当变形,发现数的高次幂,从而想到可以用二项式定理进行估算. 因此可得c 评析本解法主要是把数的大小比较进行等价变形,发现变形后的数值可以使用二项式定理进行估算,从而找出数的大小关系.遗憾的是此法对于a,c的大小关系不适用.但是此法仍然给考生以后的解题提供了一个方向[2]. 在新高考、新课标、新教材、新评价的全新理念下,国家要选拔适应社会发展的高素质、高质量人才,对学生素养要求越来越高.开展学科素养教学与跨学科教学,让学生深度学习,在运用数学知识与方法发现、提出、分析和解决问题的能力上真正地提高.本题的构造函数法就是最好的体现. 泰勒展开方法的应用则突出了新高考的选拔要求,试题要适度关注高中与高校关联的课程内容,体现高中教育与高等教育的过渡和衔接.学有余力的考生,可以适当理解掌握,更好地为高层次人才选拔服务.2方法探究
2.1 构造函数








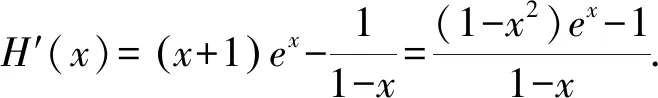



2.2 常见不等式放缩
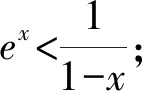
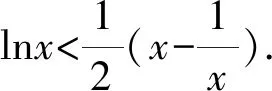
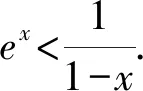



2.3 泰勒展开
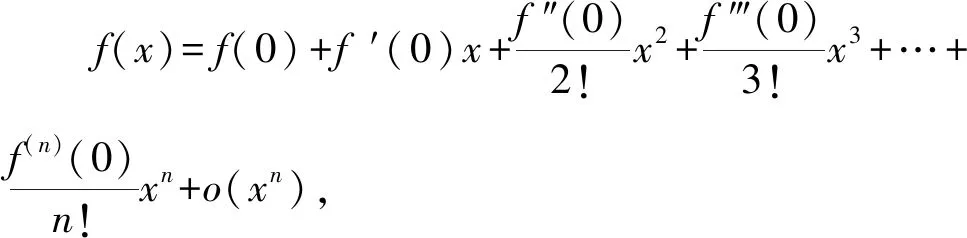
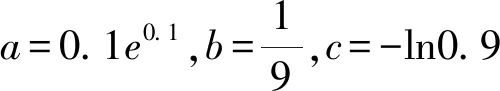


2.4 二项式定理




