工业机器人三重增量式模糊控制及其虚拟验证

孙亦劼,蒋文萍*,闵 军,汪凌阳

(1. 上海应用技术大学电气与电子工程学院,上海 201418;2. 同济大学电子与信息工程学院,上海 201804)

1 引言

随着现代工业机器人技术的不断发展,越来越多的高性能算法被广泛地应用到工业机器人的生产、教育与科研中,同时,也对我国的工业机器人算法领域的创新和验证提出了更高的要求[1]。

文献[2]提出利用极限学习机(ELM)算法对工业机器人定位误差规律及其补偿问题进行分析,得出采用ELM算法建模的补偿速度快,泛化性能好的结论。文献[3]提出了一种计算简便,并且能够有效地反映双臂协调运动灵活性性能指标的方法,提高了双臂冗余度机器人在其交互工作空间中的协调运动能力。文献[4]采用模糊神经PID算法对机械臂进行运动学/动力学控制,并证明了其控制策略的有效性和实用性。

上述文献方法虽然在一定程度上提升了机器人控制效果,但是很难预测工业机器人在实际工业环境下即将面临的问题,且无法有效地对工业场景进行真实还原。基于上述问题,提出了一种将三重增量式模糊PID控制方法与工业机器人虚拟验证相结合的研究方法。三重增量式模糊PID控制方法根据工业机器人在三维笛卡尔坐标系(空间三轴上的)末端实时位置、速度与期望位置、速度间的误差,使用三个独立的模糊控制器分别对末端三轴位置进行跟踪,经过机器人运动学计算,推导出各个关节角;而机器人虚拟仿真技术则最大程度上还原了真实工业场景,可有效避免碰撞、轴超限、奇异点等报错情况的发生。并以工业机器人喷漆操作为例,有效验证控制算法投入工业应用的可行性。

2 机械臂及其运动学建模

2.1 机械臂机械模型及其连杆参数

研究对象为三自由度串联工业机械臂,其模型的搭建由CAD软件SOLIDWORKS 2019完成。从机械臂的基座底部,到第一个左右旋转关节几何中心的距离0.6m;机械臂两个上下俯仰关节之间的机械臂称为大臂,大臂的长度为0.6m;从机械臂的第二个俯仰关节,到机械臂末端顶端的距离,即小臂加上末端的长度为0.4m[5]。机械模型如图1所示,连杆参数如表1所示。

表1 三自由度机械臂D-H参数

图1 机械臂机械模型

2.2 机械臂运动学建模

根据表1中的三自由度机械臂D-H参数,以及机器人正运动学连杆变换,得到该机械臂的总变换矩阵[6]。总变换矩阵可以描述为

0T3=A1A2A3

(1)

式中,A1、A2、A3分别为机械臂从基座到旋转关节、从旋转关节到俯仰关节、从俯仰关节到机械手末端的三个变换矩阵。其中,变换矩阵为

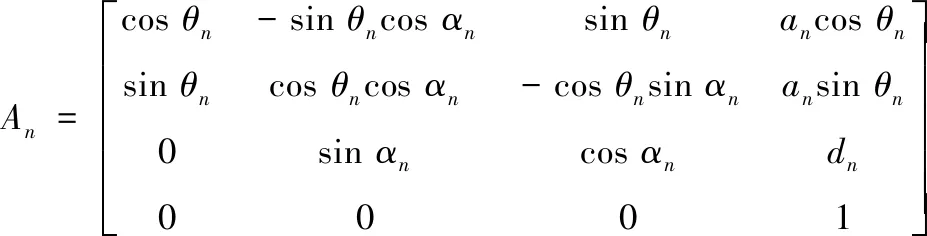
(2)

将表1中的连杆参数代入到式(2)中,得到

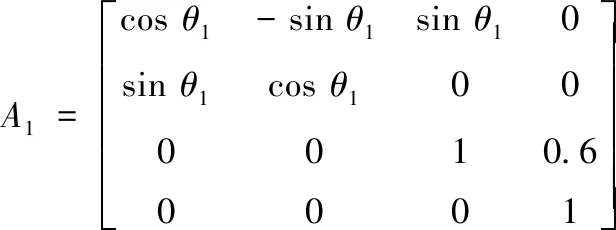
(3)

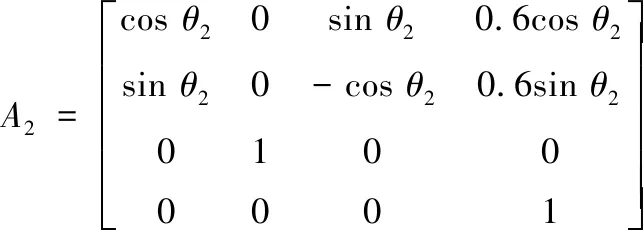
(4)

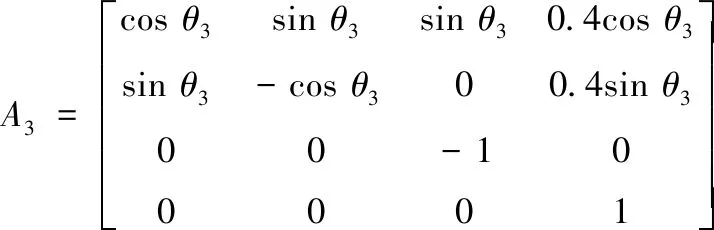
(5)

将式(3)、(4)、(5)分别代入到式(1)中,得到三自由度机械臂的总变换矩阵。

设a1为机器人的旋转机械臂,a2和a3为机器人的俯仰机械臂。过机器人末端点P(X,Y,Z)作XY平面的法线,过基座与第一旋转轴几何中心点作法线的垂线。L1、L2、L3分别为第一旋转轴到法线、末端到第一旋转轴所在平面、第一旋转轴到末端的距离[7],则有

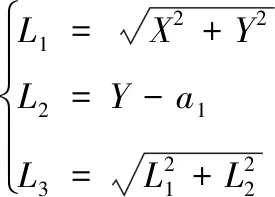
(6)

L1、L2、L3的长度已知,可以计算出q、w、e三个角度值

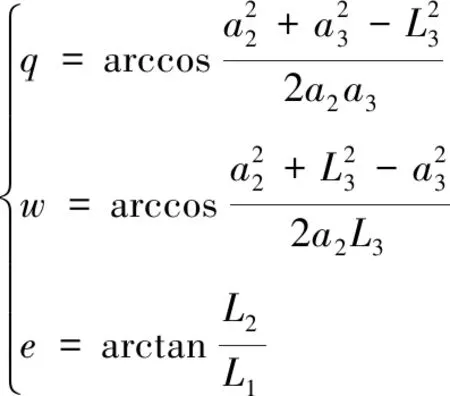
(7)

根据机器人逆运动学,θ1、θ2、θ3角度值可由式(6)(7)进行描述

(8)

3 机械臂控制器设计

机械臂三重增量式模糊PID控制器由机械臂运动控制器、机械臂三重增量式模糊PID控制器、机械臂被控系统三个模块组成。其中:机械臂运动控制器负责由期望位置Rx、Ry、Rz,末端期望速度Vx、Vy、Vz以及实际位置RX、RY、RZ,实际末端速度VX、VY、VZ,计算得到三维矩阵[8]。三重增量式模糊PID控制器将轨迹误差e以及速度误差de作为输入,结合隶属度函数,输出对应的三组Kp、Ki、Kd参数,分别控制机械臂末端在三维环境下X、Y、Z轴上的位置和速度;机械臂被控对象模块负责将三组Kp、Ki、Kd参数以及轨迹误差e通过积分环节后的累计误差E,利用雅可比矩阵以及机器人运动学,计算末端的实际位置位置RX、RY、RZ以及末端实时速度VX、VY、VZ。

3.1 机械臂运动控制器

首先,输入机械臂末端X、Y、Z轴上关于时间的期望运动轨迹

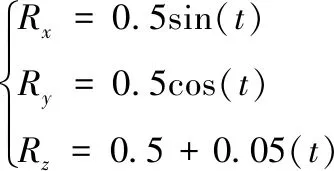
(9)

对期望轨迹求导,得到机械臂末端在X、Y、Z轴上关于时间的期望运动速度

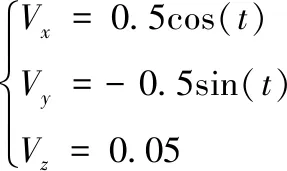
(10)

根据在2.1节中定义的机械臂臂长,由机器人运动学,得到机械臂三关节的期望角度qd1、qd2、qd3

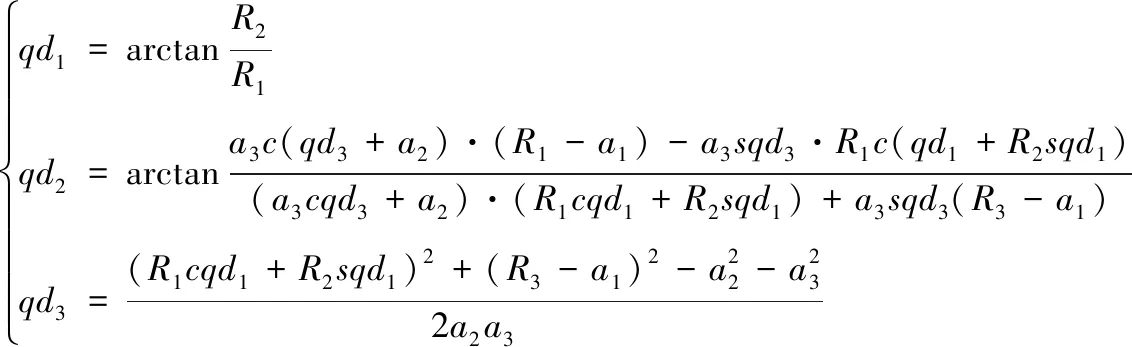
(11)

式中,c代表cos,s代表sin。

根据运动控制器的输入和被控系统的反馈输出得到三个矩阵,分别是实际轨迹与期望轨迹的误差矩阵e,位置变化量(速度)误差矩阵de,以及轨迹误差矩阵经过积分后得到的累积误差矩阵E

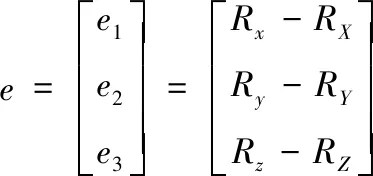
(12)

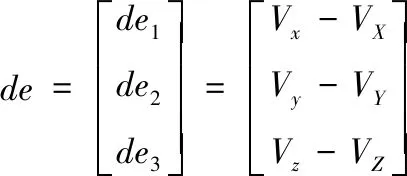
(13)

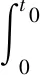
(14)

3.2 三重增量式模糊PID控制器设计

三重增量式模糊PID控制器由3个独立的模糊PID控制器组成,每个模糊PID控制器分别负责对每个空间维度上的位置和速度进行控制[9,10]。输入中,负大和正大的隶属度函数是论域为[-3,3]的高斯隶属度函数,分别为

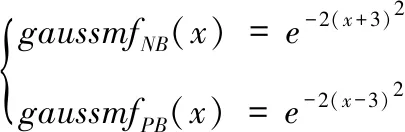
(15)

输入中负中,负小,零,正小,正中的隶属度函数是论域为[-3,3]的三角形隶属度函数,其参数分别为

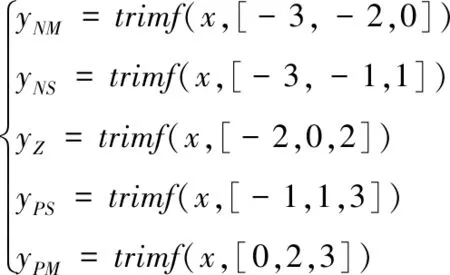
(16)

输出Kp的隶属度函数可以描述为

(17)

输出Ki的隶属度函数可以描述为

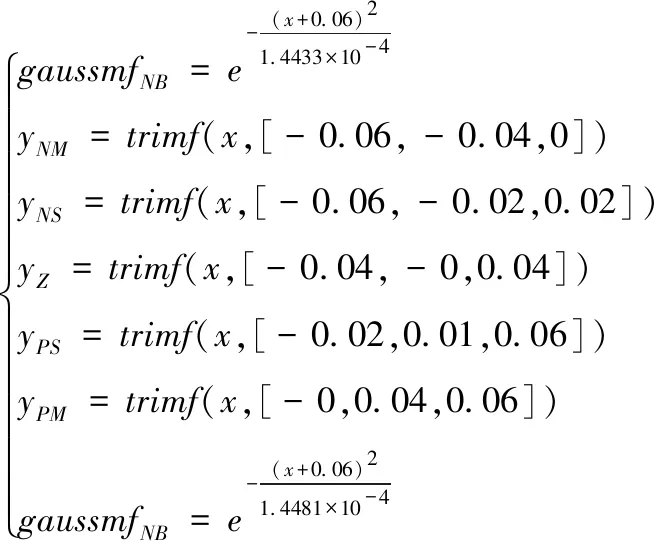
(18)

输出Kd的隶属度函数可以描述为

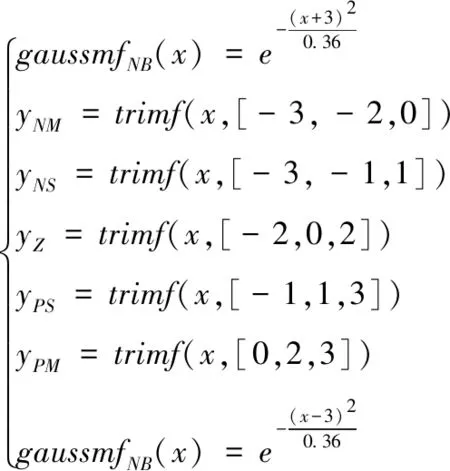
(19)

3.3 机械臂被控系统

根据上文提到的隶属度函数,得到实际机械臂被控系统中三关节的KP、KI、KD参数[11],可用三维矩阵描述为

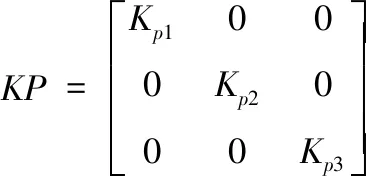
(20)

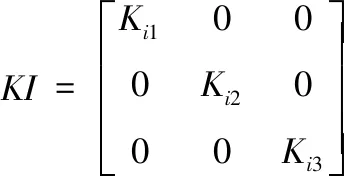
(21)

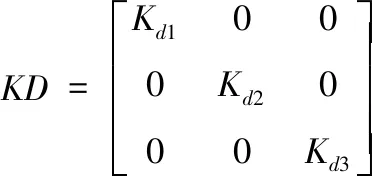
(22)

联合式(12)、(13)、(14)和式(20)、(21)、(22),可以得到一个三维矩阵

dq=KP·e+KI·E+KD·de

(23)

根据式(11)和式(23),得出机械臂关节实际角度为机械臂关节的期望角度与关节控制量之和[12,13]

(24)

由式(24)以及机械臂长度,得到机器人的雅可比矩阵J

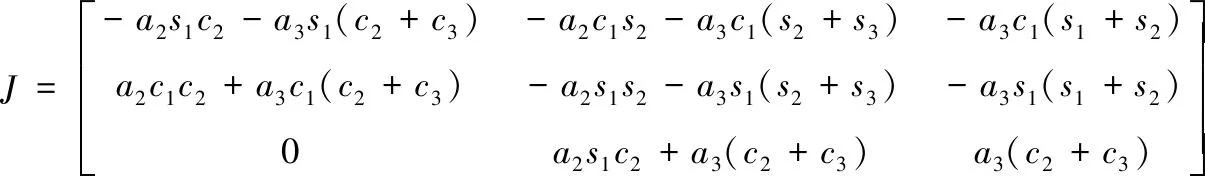
(25)

由式(23)和(25),得到机械臂末端线速度为机器人的雅可比矩阵点乘机械臂三关节控制量

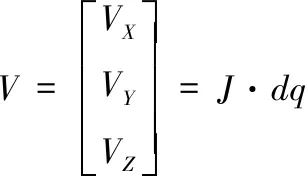
(26)

由式(24)、机械臂三臂长度以及机器人运动学,可得到机械臂末端随时间的实际运动轨迹[14,15]：

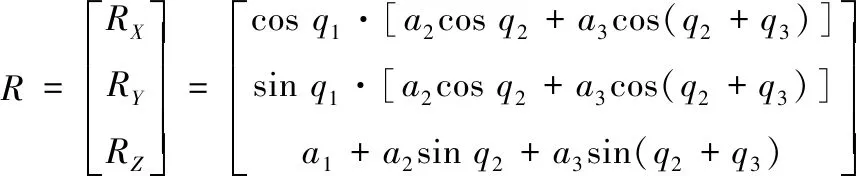
(27)

4 仿真与实验

4.1 算法仿真

根据机械臂控制器,通过计算机械臂三关节的实时角度,以及雅可比矩阵,可以得到机械臂末端的位置以及线速度,从而计算出机械臂的轨迹误差以及位置变化量误差,结合三重增量式模糊控制器,得到机械臂三个坐标下的KP、KI以及KD。将这个过程如此循环,得到定步长为0.1s下的机械臂跟踪曲线。

由式(9)和式(27),得到机械臂末端的期望轨迹及由机械臂控制器得到的实际跟踪轨迹,并将其文献[2]方法与文献[3]方法得到的跟踪轨迹进行了比较,如图2所示。

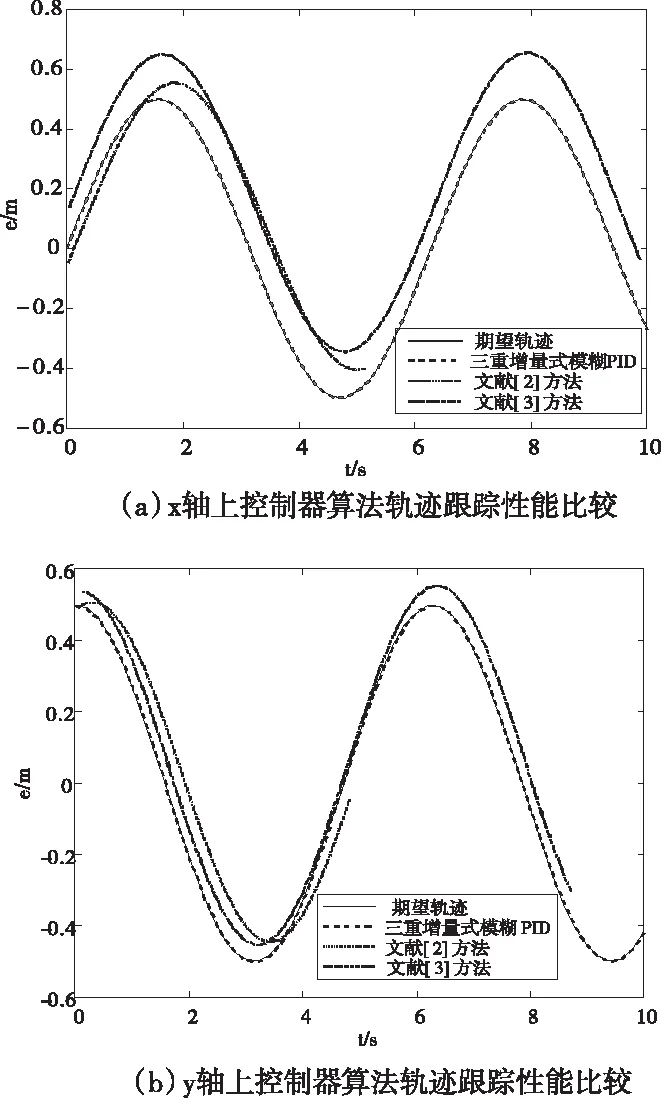
图2 轨迹跟踪性能比较

如图2所示:三重增量式模糊PID控制器在X、Y、Z轴上的跟踪表现良好,其跟踪轨迹与期望轨迹间的平均误差绝对值分别为6.421×10-5m、2.942×10-4m、1.300×10-3m,其性能远优于文献[2]和文献[3]方法的跟踪误差。

4.2 工业机器人控制算法虚拟仿真验证

验证可以分为四个阶段,依次是导入模型、定义机构、导入轨迹以及虚拟仿真。其中,导入模型阶段即将CAD中绘制的机械臂模型,导入到机器人虚拟仿真软件中;定义机构阶段包括定义机械臂自由度、定义机械臂关节以及定义机械臂限位。

导入轨迹阶段即将由三重增量式模糊PID算法输出的轨迹,导入到机器人虚拟仿真软件中,对算法输出轨迹进行验证。将控制算法得到的每一个步长点,依次输入至机器人虚拟仿真软件中(从0s-10s,步长为0.1s)。在导入轨迹工作完成后,根据输入每个步长的轨迹点,虚拟仿真软件会根据其机器人逆运动学,推导出对应位置时其各关节的角度。以对螺旋管进行喷漆为例,通过虚拟仿真,实时观察机械臂在虚拟环境下的运动情况,如图3所示。

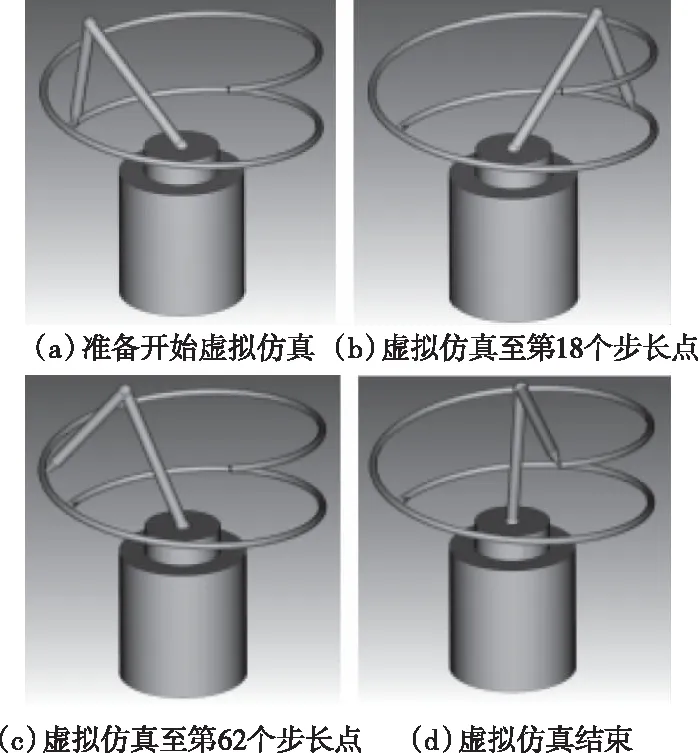
图3 对螺旋管进行虚拟仿真喷漆

5 结束语

对三自由度机械臂进行运动学建模,设计三自由度机械臂三重增量式模糊PID控制器,并将输出的机械臂运动轨迹导入到虚拟仿真软件中对控制算法进行验证。实验得出以下结论:

1)三重增量式模糊PID控制器对机械臂的期望轨迹有很好的跟踪效果,且相比于传统方法,运算速率更快,跟踪性能更优,其平均误差仅为1.300×10-3m。

2)在虚拟仿真验证算法的过程中,所有的步长点均可达,各个关节角均在轴限范围内,顺利对螺旋管完成喷漆操作。

综上,验证了该算法在实际工业情况下的可行性。