基于校正环节与改进LADRC的并网电压控制

袁昌盛,程度煦,周雪松

(1. 中国电子科技集团公司第十六研究所,安徽 合肥 230000;2. 天津理工大学电气电子工程学院,天津 300384)

1 引言

随着全球经济发展,对化石能源的需求量在不断增加,但随着时间推移化石能源会不断的枯竭,而风能是用之不竭的,因此发展风力发电是一种趋势[1-3]。在风力发电系统中并网逆变器有着广泛的应用,但其耦合性强,易受内外扰动影响,甚至导致系统失稳,需采取相应的控制策略加以抑制。因此分析并网逆变器的控制策略,抑制扰动对电网稳定的影响,保证风电并网逆变器在多种工况下的稳定运行,对风电系统在正常条件下工作有非凡的意义。

目前用于稳定网侧直流母线电压的方法较多。各种控制策略各有优点和适用限制:主从控制策略加强直流母线电压的稳定性,但是在技术上的设计比较困难,主要是由于网侧与机侧在控制系统方面相互耦合[4];下垂控制可实现有功与无功的无互联控制,并且控制的模式较为灵便,但是较难实现电网电压的安稳定运行[5]。文献[6,7]应用LADRC策略对网侧直流母线电压进行了控制,提高了信号的跟踪与抗干扰能力,但是参数添加了一倍,调参较为繁琐,且控制器的结构较为复杂。

综上所述,已有一些文献利用LADRC稳定并网直流母线电压,但都未考虑到参数众多与结构简便的问题。本文提出的策略是在传统LADRC基础上简化,并参照超前滞后的思想将LESO中的参数改进,且将其微分环节引入总扰动支路中。通过上述的改善不但使LADRC的结构得到简化,且很好的提高了LADRC扰动观测能力与抗干扰性能。

2 网侧逆变器的数学模型

图1是网侧逆变器结构图,Rg为网侧等效电阻,Lg为网侧滤波器电感,Cg为网侧滤波器电容。

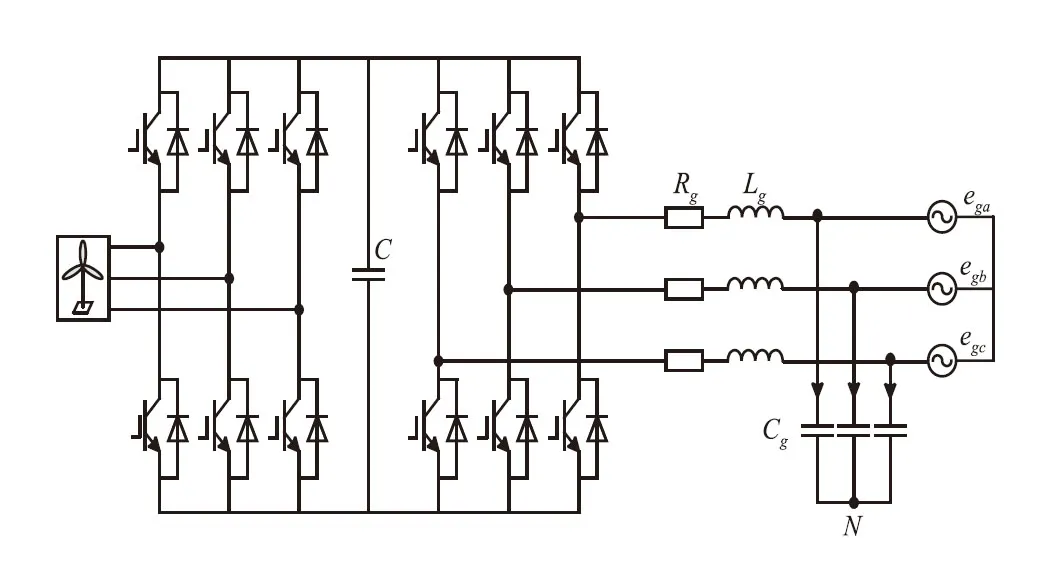
图1 网侧风电逆变器的结构图

根据风电系统的拓扑结构,得到KVL三相电压方程为

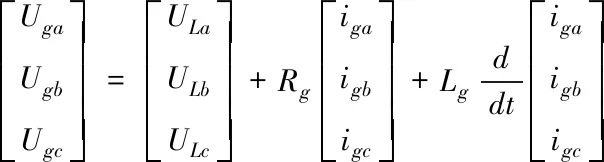
(1)

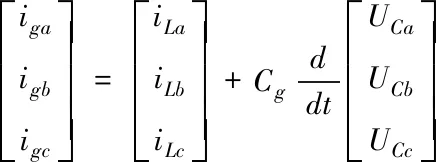
(2)

式中:Uga、Ugb、Ugc、iga、igb、igc是三相网侧逆变器的电压与电流;ULa、ULb、ULc、iLa、iLb、iLc分别为输出电压与电流。

经坐标变换转换后,可知

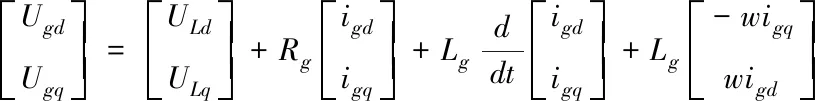
(3)

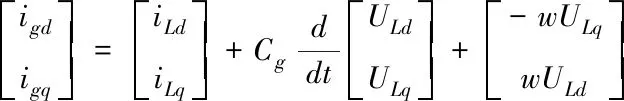
(4)

式中:Ugd、Uqd、igd、igq分别为网侧逆变器电压与电流在d、q轴上的分量;ULd、ULq、iLd、iLq分别为d、q轴上的输出电压分量与电流分量,w为电角速度。

对(3)式进行求导化简,并且将(2)式代入其中可得

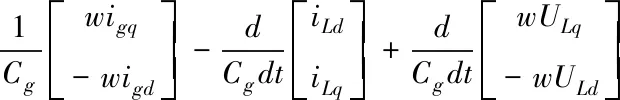
(5)

由式(5)知,风电网侧逆变器是一个多变量和耦合性较强的系统,因此应用传统控制策略不能很好达到工业要求的控制标准。

3 改进LADRC的设计

LESO是LADRC主要组成部分,由于其扰动观测性能是LADRC发挥作用的关键,因此在传统LESO的基础上进行相应的改进。

根据文献[8]可得传统LESO中扰动传递函数

(6)

由于高阶系统与二阶系统在中低频的频率特性是类似的,故上述三阶系统可以近似作为二阶系统来研究。

由上式(6)三阶系统可得二阶系统为

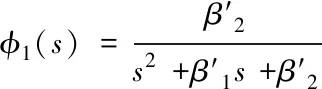
(7)

通过上式扰动观测传递函数表达式分析可知,传统的LESO在快速性与无超调上存在着矛盾,此特征表明传统的LESO在扰动观测方面表现的不够优越。

由上式(7)和典型二阶系统相对比可知

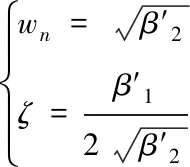
(8)

式(8)中,wn是标准二阶系统中角频率,ζ是阻尼比。

二阶系统中的上升时间和超调量等因素主要取决于wn和ζ。而参数β′2的变化可同时影响wn和ζ。即β′2参数对系统动态与稳态性能作用是最大的。

本文根据上述分析对传统LESO中的β′2进行改进,其主要是参考超前滞后的思想。

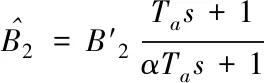
(9)

式(9)中Ta为时间常数;a是0～1中的系数,则新型LESO的扰动观测传递函数为

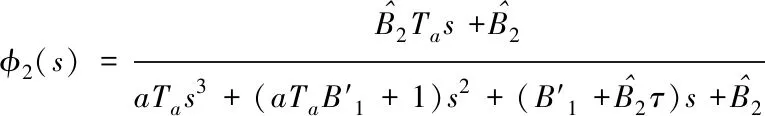
(10)

式(7)和式(10)相比,多了一个左半平面的零点,系统的根轨迹向左偏移,加强了系统的稳态与动态特性能。

为进一步提高扰动观测性能,在总扰动支路中引入超前滞后环节,则改进LESO扰动观测传递函数为

(11)

图2是三种LESO在Bode图上的性能对比;综合分析了解改进LESO观测器带宽得到更大程度增加,提高了扰动观测能力显著,且在中频段的时候,相位滞后的现象得到解决。

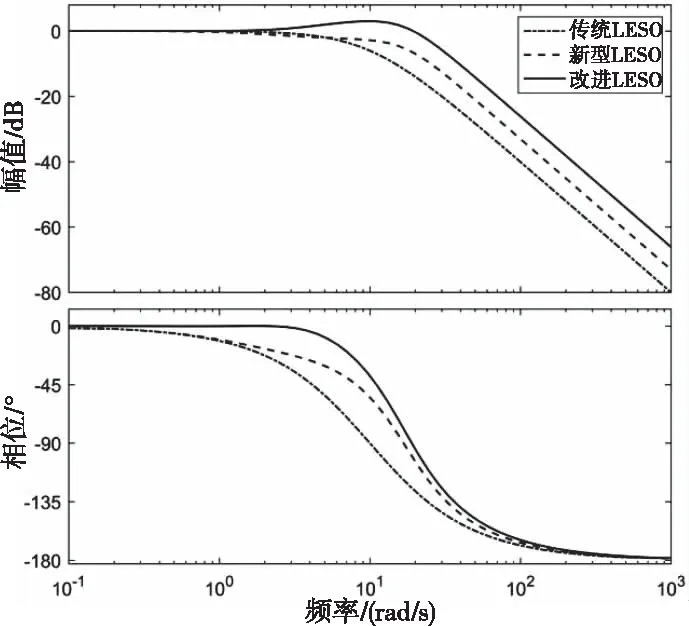
图2 三种LESO频域特性曲线

4 稳定性分析

针对本文所提的模型,证明其稳定性。

由文献[9]可知LESO表达式为

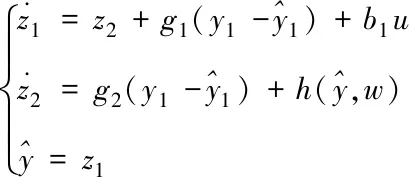
(12)

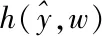
(13)

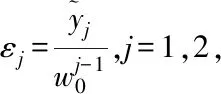
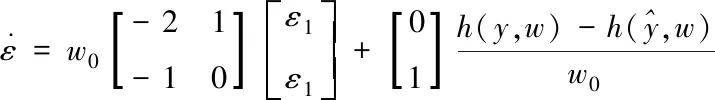
(14)

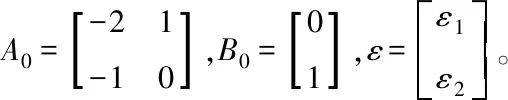
定义李雅普诺夫函数V(ε)=εTNε,则

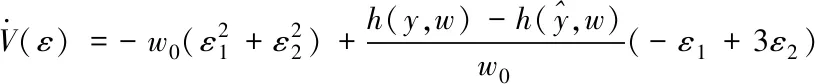
(15)

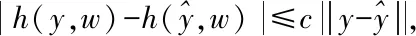
(16)

又由-ε1+3ε2=2εTNB0,式(16)可化为

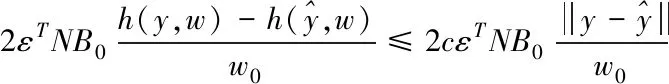
(17)

(18)

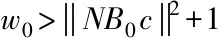
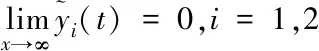
(19)

由文献[9]可知:

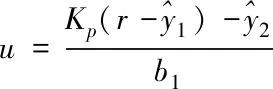
(20)

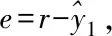
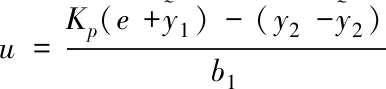
(21)

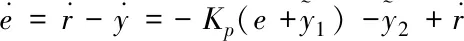
(22)

利用最值误差的控制信号使被控对象得到激励,可将输出信号快速流出去。则系统变成

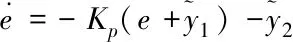
(23)

将式(23)写成状态空间形式为

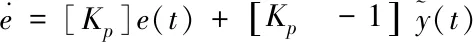
(24)

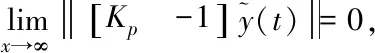
5 仿真与分析

为验证本文所设计的控制系统的性能效果,在MATLAB/Simulink平台上展开相关的仿真分析,1.5MW永磁风电机组控制模型如下图3所示。在仿真分析当中,本文和文献[10]中提出的传统LADRC进行对比分析,利用文献[10]的参数进行仿真验证。

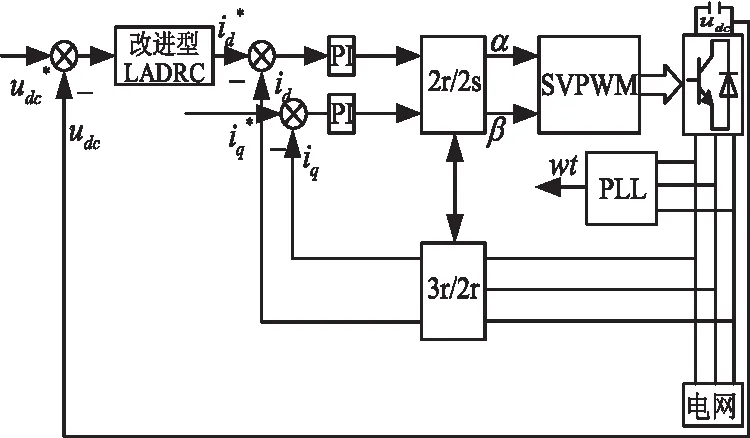
图3 改进型LADRC控制仿真图

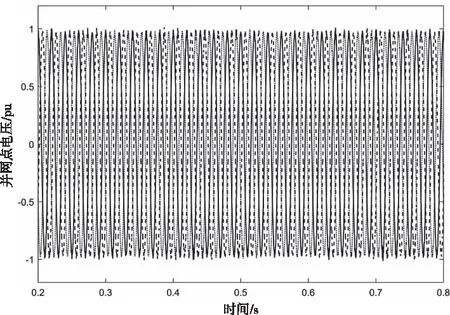
图4 对称工况下的并网电压波形

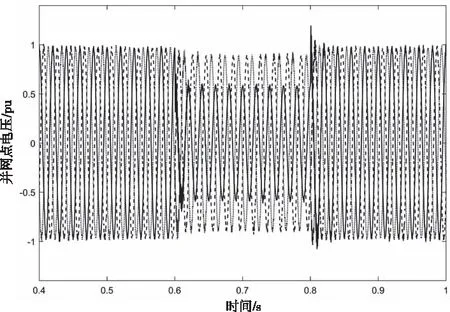
图5 不对称工况下的并网电压波形

选用的并网逆变器与控制器参数分别为:PN=1.5MW,U网侧线电压=690V,U直流母线电压=1070V,C=240μF,L=20μH,R=0.942Ω;wc=2500rad/s,w0=700rad/s,b0=12000。

1) 设置工况开始时间为1.0s,结束时间为1.2s;则加载60%工况下的直流母线电压如图6所示。

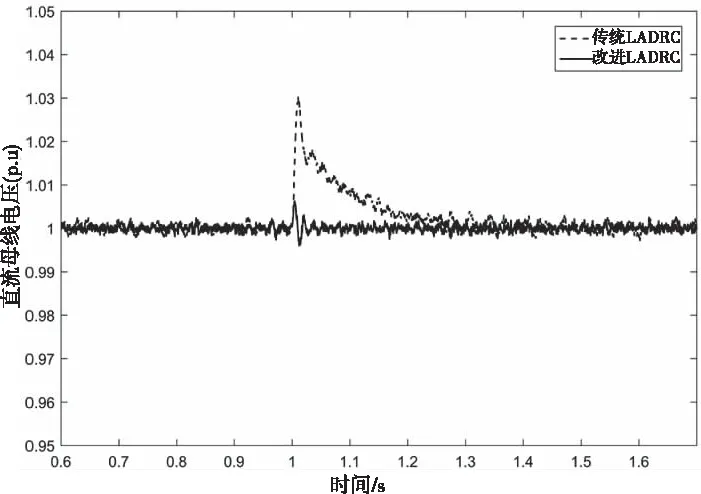
图6 加载60%工况下的直流母线电压

2) 设置工况开始时间为1.0s,结束时间为1.2s;则减载60%工况下的直流母线电压如图7所示。

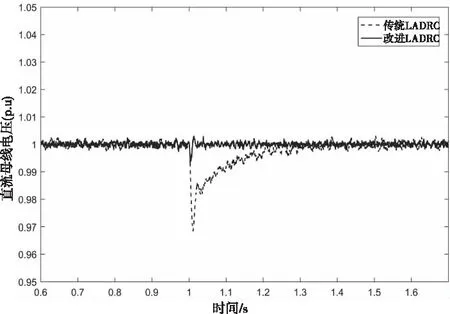
图7 减载60%工况下的直流母线电压

3) 设置工况开始时间为0.6s,结束时间为0.8s;则对称跌落40%工况下的直流母线电压如图8所示。

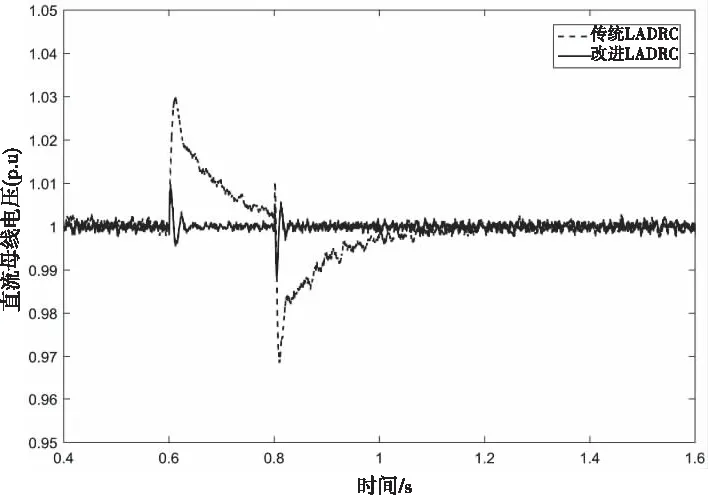
图8 对称跌落40%工况下的直流母线电压

4) 设置工况开始时间为0.6s,结束时间为0.8s;则不对称跌落40%工况下的直流母线电压如图9所示。

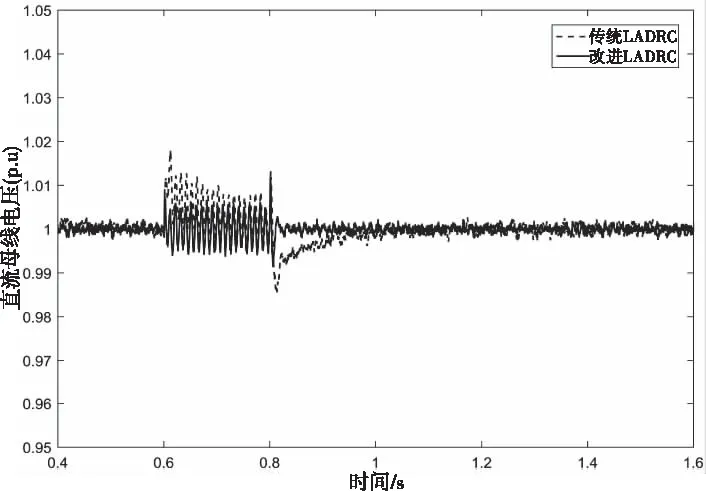
图9 不对称跌落40%工况下的直流母线电压

图6与图7分别是加载和减载工况下的直流母线电压波形,传统LADRC加载工况下超调量为0.03pu,改进LADRC超调量为0.01pu;在减载工况下传统LADRC的超调量为0.03pu,改进LADRC的超调量为0.01pu。图8与图9分别是对称与不对称跌落40%下的直流母线电压,在对称跌落工况下传统LADRC超调量为0.022pu,改进LADRC超调量为0.008pu;在不对称跌落工况下传统LADRC超调量为0.015pu,改进LADRC超调量为0.001pu。通过上述多种工况结果对比分析可知,改进LADRC具有可行性和先进性。

6 结论

本文针对风电并网逆变器输出的直流母线电压稳定性易受外部干扰的问题,设计了超前滞后的微分环节与传统LADRC相结合的改进型LADRC,最后通过理论与仿真对改进型LADRC控制策略展开分析。其得出的结果如下:①改进的LADRC有更好的抗扰与稳定性能;②由于实验条件有限,没有进行实物仿真,仅在仿真软件上进行验证,可能在细节上出现些许误差。