分数“量”含义的学习路径研究

金晶 周琪 孙瑞 巩子坤

【摘   要】在利用“个”情境模型初步认识分数“量”含义的基础上，探讨了利用“米”“时”情境模型巩固分数“量”含义的学习路径：复习“个”情境模型—引入“米”“时”情境模型—巩固分数“量”含义—应用分数“量”含义。结果表明，基于“米”“时”情境模型的分数“量”含义的学习路径有效巩固了学生对分数“量”含义的理解。可见，研究设计的学习路径有助于学生体会分数产生的必要性，感受分数的本质，加深对分数“量”含义的理解。

【关键词】分数；“量”含义；情境模型；学习路径

一、引言

前文《分数“量”含义的学习路径研究——基于“个”情境模型认识分数“量”含义》［1］通过三次教学设计、两次教学实践以及多次教学研讨，最终得到了完善的学习路径。在该学习路径中，教师基于“个”情境模型，引领学生感受分数产生的必要性，体会分数本质，初步认识分数“量”含义。

学生对分数“量”含义的理解并非一蹴而就的，单纯地通过“个”情境模型并不能让学生深刻理解分数“量”含义。因此，本研究将在“个”情境模型的基础上，开展分数“量”含义第二课时的教学。

整数知识是分数概念习得的基础，是学生学习、理解分数概念的支撑，也是重要的认知“固着点”［2-4］。本研究充分发挥整数知识对分数学习的促进作用，选取与学生生活紧密相连、具有可操作性的“米”“时”情境模型，促进学生对分数“量”含义的进一步理解。具体而言，主要围绕以下两个问题展开：（1）如何利用“米”“时”情境模型，构建有效的学习路径，从而促进学生对分数“量”含义的进一步理解；（2）如何在两课时的分数“量”含义教学后，验证本研究重构的学习路径的整体效果。

二、研究設计

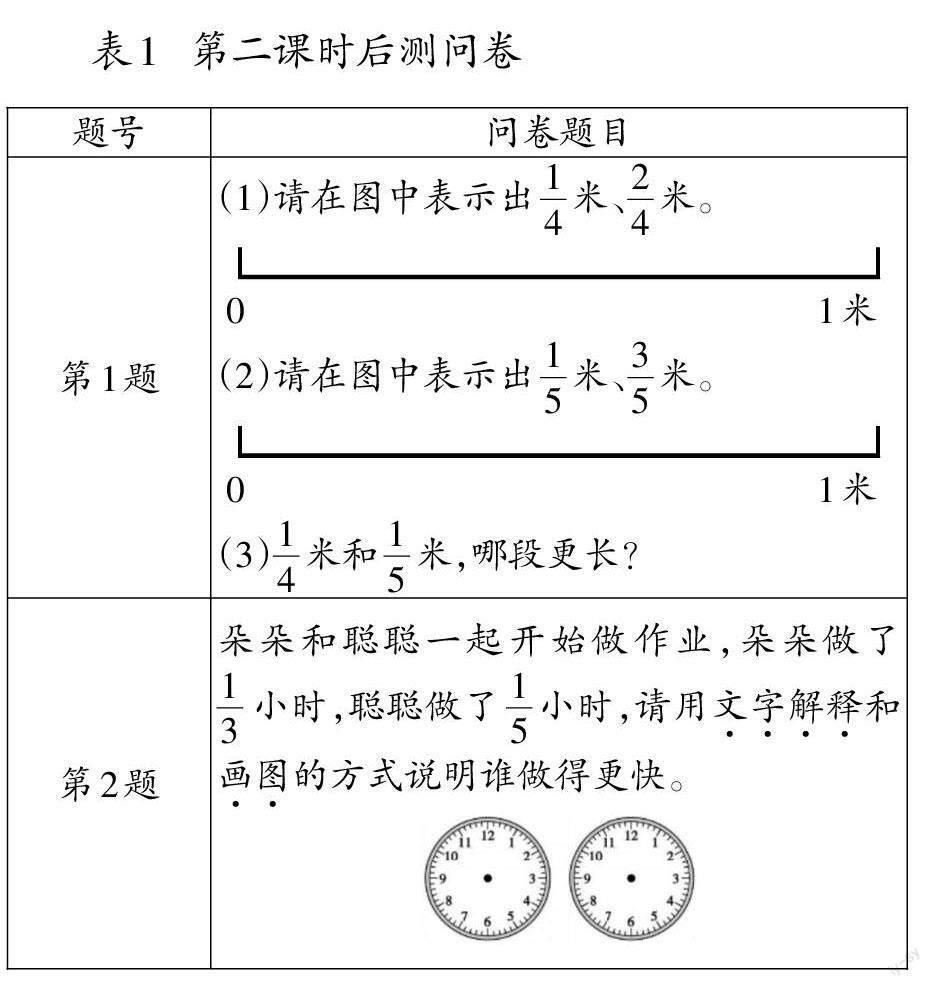
为了回答上述问题，继续在杭州市YH小学三年级甲、乙班开展研究，SH小学的丙、丁班仍按正常教学进度开展教学。相关研究流程和分数概念理解类型［5］如前文，第二课时后测问卷如表1所示。

具体评分标准如下：画图正确得1分（直观理解），其中第1题第（1）（2）小题画图正确各2分，第2题画图正确2分，共6分；大小比较正确得1分（符号理解），对应第1题第（3）小题；文字解释合理得1分（抽象理解），对应第2题。总分为8分。依此给学生问卷赋分，并分别统计学生在直观理解、符号理解、抽象理解上的得分。

三、研究结果与分析

（一）假想的学习路径B1

1.路径呈现

基于相关研究与前测结果，拟定假想的学习路径B1，如图1所示。

任务1从[12]个、[13]个比萨入手，复习巩固“个”情境模型在分数“量”含义中的运用。

任务2分别以“米”“时”情境模型拓展学生对“量”含义的认识，让学生感受到分数不仅出现在“个”情境中，在其他情境中也有“量”含义的分数。

任务3为了更好发挥整数知识作为认知固着点的作用，借助米尺和时钟两种教具，给予学生充分的机会和充足的时间去操作、体验。具体教学片段如下，其中T是教师，S是学生。

T：我们请选择米尺的同学来汇报一下，说一说他是怎么找到[12]米和[13]米的。

S：把米尺像这样对折一下，就可以找到[12]米，在50厘米处（如图2）。把米尺折成3段，就可以找到[13]米，大约在33厘米处。

由此可见，随着米尺的引入，学生能够通过折米尺找到[12]米、[13]米，并看着尺子说出50厘米、33厘米，而不是简单地通过换算单位再作除法来解决问题。这不仅保证了学生能够以整数知识为认知固着点来充分认识分数“量”含义，也有助于学生在后续学习任务中正确比较单位分数以及同分母分数的大小。

任务4承接任务3中的“对米尺和时钟进行操作”这一任务，要求学生观察自己所操作的材料，找到非单位分数并进行大小比较。

2.存在问题与改进建议

（1）学生自主思考时间较少

综观整个教学过程，不论是“米”“时”情境模型的引入，还是活动性任务的开展，都没有给予学生太多思考时间。例如，“米”“时”情境模型都是由教师直接告知学生，而并非学生自己想到的，学生没能很好地体会到分数“量”含义可以出现在多个情境之中。此外，学生在动手操作的过程中不仅能发现单位分数，也能找到非单位分数，但教师仅要求学生找到[12]米和[13]米、[12]时和[13]时，这在某种程度上束缚了学生的思维。

为此，教师可以只介绍“米”情境模型，并鼓励学生以此为范例，思考还有什么单位也可以用[12]进行描述，进而聚焦到“时”情境模型。此外，教师设计活动性任务时可以更加开放，鼓励学生以独立思考、组内交流的形式，通过折一折、画一画、剪一剪，发现新的分数。

（2）任务无趣，课堂思维含量不高

尽管教学模型由“个”转化为了“米”和“时”，但从学生的角度来看，只是换了个学习材料，略显枯燥无趣。在课后访谈环节，许多学生反馈，分数的大小比较在上一堂课已经学过了，并不具有挑战性。可见，本课时的思维含量并不高。

为了提高课堂思维含量，专家团队建议教师在带领学生比较单位分数以及同分母分数的大小后，鼓励学生总结分数大小比较的规律。同时，可以增加应用思考题“1只猫和1只狗比，谁重”（如图3），为学生提供将新的知识学以致用的机会。应用题能够有效激起学生的好胜心，引导学生在通过分数解决并“说清楚”问题的过程中感悟分数的魅力，从而增强学生对分数“量”含义的理解。

（二）优化的学习路径B2

1.路径呈现

团队经过研讨，对学习路径进行了优化，优化后的路径如图4所示。

与路径B1相比，路径B2的教学逻辑更加清晰，教学环节更加合理，学生的课堂表现也更加活跃，但仍存在可完善之处。例如，在小组汇报展示“时”情境模型时（任务3.1），有学生说：分针走一圈表示12个小时，将一圈平均分成12段，1段就是[112]小时。很显然，这是不对的。这说明学生一开始就未明确“分针转一圈表示1小时”，且教师并未纠正这一点。具体教学片段如下，其中T是教师，S是学生。

T：这个小组完成得很好，其他小组有找到不一样的分数吗？

S：我找到了[112]时。

S：分针转一圈表示12时，一圈可以平均分成12段，1段就是[112]时。

为此，教师应当在“时”情境模型出现伊始，便强调“分针转一圈表示1小时”，从而在学生心中牢固树立这一观点。

最终完善的学习路径B3与学习路径B2大致相同，不再详述。

2.路径效果检验

在路径B1和路径B2实施后，依次对甲、乙班学生进行后测，统计学生三种理解类型的得分率和班级平均分，其中乙班学生的班级平均分（6.87分）明显高于甲班（4.80分）。独立样本t检验结果显示，学生的直观理解得分（t=1.355，p=0.182）不存在显著性差异，符号理解得分（t=1.868，p<.05）、抽象理解得分（t=2.4766，p<.05）及班级平均分（t=-2.995，p<.05）存在显著性差异。可见，路径B2的效果优于B1，更有利于学生巩固对分数“量”含义的理解。

四、学习路径总体效果

为检验本研究重构的两条学习路径的总体效果，在实验班授课结束两周后，教师组织学生进行了综合测试（题目来源于第一课时、第二课时后测，由5道大题组成，满分17分）。其中3题来源于第一课时后测，共9分；2题来源于第二课时后测，共8分。同时进行了综合测试分析和对照分析。其中，综合测试分析是为了探查实验班学生在后测与综合测试中的得分变化情况，对照分析是为了探查实验班学生和对照班学生在综合测试中的差异。

（一）综合测试分析

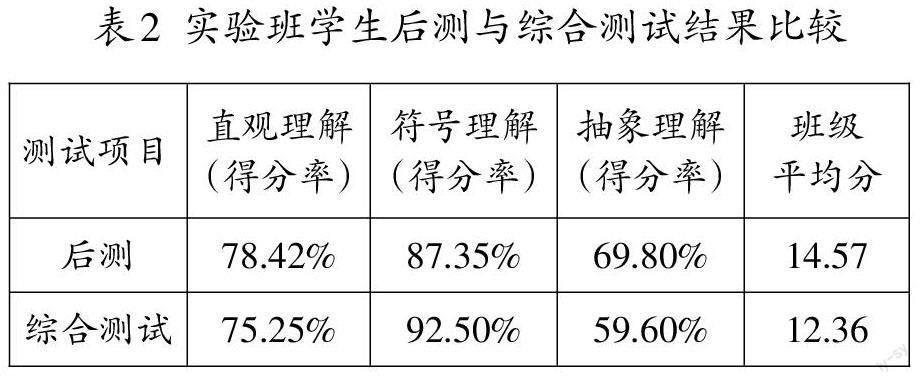
对实验班学生的后测与综合测试的得分进行配对样本t检验（如表2），结果显示，班级平均分（t=0.091，p=0.926）、直观理解得分（t=1.201，p=0.232）与符号理解得分（t=0.933，p=0.968）均不存在显著性差异，抽象理解得分（t=-1.867，p<.05）存在显著性差异。

在这期间，实验班学生未针对分数“量”含义进行作业巩固，对上课内容会有一定程度的遗忘，因而测试得分会略低于学生最初学习分数“量”含义时的水平。即便如此，学生的直观理解得分也并没有出现明显的退步，甚至符号理解的得分率还有所提升。相较而言，学生抽象理解的得分率出现了显著性差异，这或许是因为学生在日常学习中，鲜少用抽象表征来表示分数“量”含义，从而导致得分有所退步。

综上可知，本研究所设计的两条学习路径使学生对分数“量”含义有了深刻的理解，依据此学习路径开展的教学是有效的。

（二）实验班、对照班分析

对实验班和对照班学生的综合测试得分进行独立样本t检验（如表3），结果显示，直观理解得分（t=-1.254，p=0.173）不存在显著性差异，班级平均分（t=3.605，p<.05）、符号理解得分（t=3.734，p<.05）与抽象理解得分（t=3.189，p<.05）存在顯著性差异。

可见，与现行教材设计的学习路径相比，本研究设计的学习路径更侧重于培养学生的符号理解和抽象理解能力，这样的教学有助于加深学生对分数“量”含义的理解。

五、研究结论与建议

（一）研究结论

在教学过程中，教师聚焦“米”“时”情境模型，依次带领学生复习“个”情境模型、认识“米”“时”情境模型、巩固分数“量”含义、应用分数“量”含义，不仅拓宽了学生的视野，发散了学生的思维，也加深了学生对分数“量”含义的理解。除此之外，动手操作环节充分调动了学生的多重感官，既允许学生大胆创造，也促进学生在大小比较中培养自身的语言表达能力，体会分数的本质特征。

第二课时后测结果显示，与路径B1相比，优化后的学习路径B2效果更佳。综合测试分析和对照分析结果显示，实验班学生并没有出现显著退步，且实验班学生的成绩显著高于对照班学生的成绩（当然，这样的结果与实验班注重分数“量”含义的教学直接相关）。这说明本研究重构的两条学习路径在帮助学生理解分数“量”含义方面发挥着重要作用。整体而言，基于“个”“米”“时”情境模型下的两条学习路径，依次带领学生初步认识分数“量”含义、夯实巩固对分数“量”含义的理解，有助于学生体会分数产生的必要性，感受分数的本质，加深对分数“量”含义的理解。

（二）研究建议

1.基于“米”“时”情境模型巩固分数“量”含义

分数“量”含义的学习并非一蹴而就的，单纯依靠“个”情境模型还远远不够。选取贴近学生日常生活、便于学生动手操作的“米”“时”情境模型，有助于学生体会不同情境下分数“量”含义的内涵，巩固对分数“量”含义的理解。

2.充分发挥整数知识作为认知固着点的作用

整数知识能促进学生更好地理解分数含义，是学生习得分数概念的基础及非常重要的固着点。因此，教师应充分利用学生所学的整数知识，引导学生在整数知识的基础上认识分数“量”含义。例如，在动手操作环节的材料选择上，可以选取带有刻度的米尺以及无指针的时钟，并通过直观的、具体的整数，帮助学生运用分数解决问题。

3.关注任务的活动性和提高课堂思维含量

学生的感性经验是不可替代的，教师应尽可能让学生通过动手操作与亲身体会来理解分数“量”含义。例如，教师可以为学生提供米尺和时钟等教具，让学生通过折一折、画一画、剪一剪之类的操作，自主发现单位分数和非单位分数。此外，由于学生在“个”情境模型的学习中已经接触了分数的大小比较，所以在“米”“时”情境模型的学习过程中，可以适当提高课堂的思维含量，如鼓励学生总结分数大小的规律，设置应用思考题，从而引导学生感受分数“量”含义在不同情境中的运用，加深学生对分数“量”含义的理解。

参考文献：

［1］ 巩子坤，金晶，周琪，等.分数“量”含义的学习路径研究：基于“个”情境模型认识分数“量”含义［J］.教学月刊·小学版（数学），2023（3）：52-57.

［2］ 刘春晖，辛自强.五—八年级学生分数概念的发展［J］.数学教育学报，2010，19（5）：59-63.

［3］杨伊生，刘儒德.儿童分数概念发展研究综述［J］.内蒙古师范大学学报（教育科学版），2008，21（6）：130-134．

［4］ 马珂.分数概念的认识及其教学研究［D］.北京：首都师范大学，2014.

［5］ 巩子坤.有理数运算的理解水平及其教与学的策略研究［D］.重庆：西南大学，2006.

（1.杭州师范大学经亨颐教育学院

2.浙江省杭州市观成武林中学

3.浙江省杭州银湖实验小学）