孤立翼尖涡模态演化规律的实验研究
吴奕铭,邱思逸,向阳,刘洪
上海交通大学 航空航天学院,上海 200240
翼尖涡是由机翼上下表面压力差产生的一种大尺度涡结构,在飞机起降阶段,这种典型结构会威胁后续飞机的飞行安全,降低机场的起降频率[1]。为了高效地衰减翼尖涡的强度和持续时间,翼尖涡的主动控制方法逐渐受到重视。然而,对翼尖涡不稳定性认知的不足是导致翼尖涡主动控制技术发展困难的原因之一[2]。在过去翼尖涡不稳定性主动控制研究中,最有价值的研究之一是Edstrand 等[3]在2018 年利用稳定性分析方法指导翼尖涡主动衰减的研究。通过对NACA0012 机翼产生的尾涡流场进行稳定性分析,发现增长速率最小的第5 阶尾迹模态因为其独特的结构提供了激发翼尖涡不稳定性的途径,基于第5 阶模态的控制装置的性能优于基于主扰动模态的装置。但是现象背后的机制尚未表明,需要研究翼尖涡的模态演化规律,揭示次级模态随着流向发展的规律以及对翼尖涡不稳定性的影响。
在翼尖涡的不稳定特征方面,对于更贴近真实飞机飞行的反向翼尖涡对,其不稳定性特征集中在翼尖涡的少量湍流结构促进涡对的正弦形变和自诱导作用[4],根据其周期性特征可分为长波不稳定性[5]和短波不稳定性[6]。而对于一个孤立翼尖涡,其不稳定性特征主要表现为涡在流向截面内的低频振荡,即翼尖涡摇摆运动(Vortex Wandering)。这种现象最初由Baker 等[7]在水槽实验中发现,这种摇摆运动使翼尖涡物理参数的测量与求解产生误差,同时,如何消除这种摇摆运动带来的误差和其内在的物理机制一直是研究的重点。Devenport 等[8]首次通过反卷积修正法对翼尖涡摇摆现象予以修正,同时在施特鲁哈尔数St较小的条件下,观察到翼尖涡摇摆的各向异性现象。Deem 等[9]在此基础上证明翼尖涡的瞬时涡核位置分布满足高斯分布的规律。Bailey和Tavoularis[10]通过热线测量得到雷诺数105的翼尖涡摇摆的主频约在10 Hz 量级;薛栋等[11]使用单点谱分析和模态分解技术得到在雷诺数103量级下,翼尖涡的摇摆运动存在主导频率,主频率约为1 Hz。在此基础上,Edstrand 等[12]通过线性稳定性分析(Linear Stability Analysis,LSA)得到翼尖涡的主扰动模态并和翼尖涡实验数据的本征正交分解(POD)模态对比,证明翼尖涡摇摆来源于其内在不稳定性特征。Cheng 等[13]通过对孤立翼尖涡的体视粒子图像测速技术(SPIV)和线性稳定性分析进一步发现孤立翼尖涡摇摆幅值与翼尖涡的不稳定性放大率存在某种量化关系。
长期以来,翼尖涡不稳定模态的研究主要聚焦于最不稳定模态的结构特征以及最不稳定模态促进扰动增长的内在机制。孤立翼尖涡的最不稳定模态主要分为黏性和非黏性2 种情况,对无黏性的研究可以追溯到Lessen 等[14]在发现与涡旋旋转相反的方位波数为负的螺旋模态在无黏极限下是不稳定的,并且占主导地位。对于黏性情形,孤立涡则会表现出多种不稳定模态,在临界雷诺数(Critical Reynolds Number)较小的情况下,翼尖涡的不稳定性受周向波数m最低的螺旋模态影响较大(m=±1),而周向波数较高的模态(m>1)则在雷诺数较高的情况下占据主导地位[15]。Leibovich 和Stewartson[16]进行了柱状涡旋不稳定性的渐近分析,指出扰动在达到最大增长率的临界半径处的扰动峰值,与扰动的模态结构有关。Gallaire 和Chomaz[17]揭示了旋转射流双螺旋模态的模态选择机制,发现螺旋模态的选择是由离心力决定的,而轴向和方位剪切模态也是促进螺旋模式选择的主要因素。Fabre等[18]描述Lamb-Oseen 涡的Kelvin 模态和奇异本征模态,并从物理角度解释了这些模式是如何产生涡旋的。然而,对于轴向Batchelor 涡扰动增长的物理机制仍然是模糊的,Qiu 等[19]认为Batchelor 涡的扰动增长是翼尖涡最不稳定扰动模态和特征点,特征层波动相互作用的结果,给出关于扰动增长的物理机制的猜想。
翼尖涡的模态演化特征方面,文献[20-22]对孤立涡和同转翼尖涡对的最优扰动模态的结构特征和数值特征给出了详细的描述。随着雷诺数和攻角的变化,翼尖涡的主扰动模态往往也会呈现出不同的结构,这种变化尤其体现在周向波数的变化,随着雷诺数的增加,翼尖涡的主扰动模态会相应出现周向波数较大的结构[23]。同时,孤立翼尖涡的涡摇摆特征与主扰动模态关系较大,其主模态会随着时间进行周期性旋转,与翼尖涡自身的摇摆规律吻合[24]。Fabre 等[18]给出了m=−1~−5 的模态的不稳定性放大率随着雷诺数增加的变化规律,指出在高雷诺数的工况下,周向波数m较高的模态会逐渐占据主导地位,而周向波数较低的模态则会逐渐消散。但关于翼尖涡的主扰动模态随着流向发展如何演化,其演化规律随着来流雷诺数的变化是否具有统一性,仍然是未知的。同时,对次级模态演化规律的认知仍然匮乏,而次级模态对翼尖涡的主动控制也起到指导作用[18]。
综上所述,目前对孤立翼尖涡这种大型客机的翼尖涡典型结构的不稳定性现象和特征已经有了初步认识,但对翼尖涡扰动模态演化规律仍然是未知的,通过对翼尖涡扰动模态演化规律展开研究,可以为翼尖涡主动控制提供物理的理论指导[25]。同时,有关翼尖涡的次级模态随流向的演化以及对翼尖涡本身的影响的认知却一直停滞不前,这阻碍了基于不稳定性的大型翼尖涡快速失稳衰减控制原理与方法的建立,需要进一步研究和分析。因此,本文通过SPIV 测量不同工况下的翼尖涡流场,结合线性稳定性探究翼尖涡主扰动模态和次级扰动模态的结构特征,分析模态对翼尖涡流场的作用;进一步地,研究翼尖涡主扰动模态和次级扰动模态随流向的演化规律和能量增长。在此基础上,提出次级扰动模态对翼尖涡主动控制的指导思路,以期为翼尖涡的主动控制策略提供参考。
1 实验搭建与数据处理
1.1 实验设置
本文实验均在低速回流式风洞中进行。实验段尺寸为1.2 m×0.9 m,长度为7.0 m。通过调节变频器频率可实现风速的实时调整,风速范围可达10~70 m/s。收缩段前安装蜂窝网以降低实验段的湍流度,实验中的湍流度小于1%。机翼及小翼的翼型均采用M6 翼型。等直翼弦长c=0.203 m,展弦比AR=3。机翼模型均使用铝合金材料,经铣床加工并进行表面后处理,以保证曲面准度及表面光滑度。
为了实验比较,在攻角为6°、8°、10°的条件上,测试了自由来流速度U∞=15 m/s 的翼尖涡流场,基于弦长(c=0.203 m)的雷诺数为Rec=0.82×105,尾迹区内翼尖涡流场的测量范围x/c=2~16,每隔1 倍弦长c进行一次采样,其中x为流向坐标,如图1 所示。

图1 SPIV 实验设置Fig.1 Setup of SPIV experiment
1.2 粒子图像测速(PIV)系统设置
本研究中的PIV(Particle Image Velocim‐etry)系统包括风洞系统、激光系统、图像采集系统、同步系统、图像后处理系统,如图2 所示。PIV 示踪粒子需要在保证对激光散射性的基础上,直径尽可能小以满足跟随性,且其密度实验流体保持一致。实验中,通过大小为1~5 μm 的乙二醇小油滴对流动进行示踪。乙二醇小油滴由Fesco 1700 雾化发烟器产生,在实验段上游将粒子油滴通入风洞,并在风洞中循环一定时间使粒子与空气混合均匀。激光系统包括一台镭宝双脉冲Nd:YAG 激光发生器和导光臂,双脉冲能量为2×380 MJ,双脉冲频率为1 Hz,激光波长为532 nm,2 次脉冲间隔为10 μs,片光源的厚度为2 mm 并垂直于来流方向。图像采集系统包括2 台高速高分辨率CCD(Charge coupled Device)相机对激光片光源照射的流场截面进行拍摄,分辨率为2 048 pixel×2 048 pixel,并通过532 nm波长带通滤光镜来提高图像信噪比。同步系统将激光脉冲与相机快门进行同步,由1 台数字延迟信号发生器实现。图像处理系统则使用商业PIV 图像处理软件INSIGHT 4G 对PIV 图像进行互相关处理并计算速度矢量场。初始咨询窗口为72 pixel×72 pixel,有效重叠率为25%。第2 个参考窗口为36 pixel×36 pixel,有效重叠率为50%,未求解的速度向量通过9 pixel×9 pixel的填充算法从周围向量插值求得。这样,在整个测区内测速的良好率在85%以上,测速误差小于1%,满足后续分析的要求[26]。对每个截面采集200 s 流场数据,采样频率为1 Hz,并通过TSI INSIGHT 4G 软件对图像进行配对和解算,其解调范围为24 pixel×24 pixel,得到翼尖涡流场在x、y、z这3 个方向的速度,并计算得到涡量场。

图2 PIV 实验系统组成Fig.2 System composition of PIV experiment
1.3 线性稳定性分析方法
线性稳定性分析是一种通过求解基于Navier-Stokes(N-S)方程的线性化小扰动方程,得到某一基准流动(Base Flow)的各个扰动模态和其对应的不稳定性放大率、扰动频率和波数的一种方法,从而定量化判断该流动的稳定性,以及该流场中小扰动的速度分布、频率特征及其随时间/空间的发展[24]。对于具体的流动,可以对流场进行不同的假设,从而对问题进行适当简化,在减小计算量的同时也可以得到准确的结果。
对于一个给定的基准流动,考察其小扰动的模态行为,根据标准的线性稳定性分析公式,状态变量可以分解为定常基流和非定常扰动
在翼型后部的中间区域,黏性扩散相对于流向而言较为缓慢,产生准平行流动,流向梯度远大于横向梯度。这种关于基流流向变化的准平行假设导致了沿流向具有常系数的扰动方程,并允许波状扰动解的形式[27],脉动量在柱坐标系可写为
将式(4)代入线性化的扰动方程,产生一个广义特征值问题。特征值问题的具体形式取决于稳定性分析的类型。对于时间稳定性分析,假设扰动随时间增长/衰减,并考虑复频率ω=ωr+ωi,产生的特征值问题为
式中:A、B为稳定性矩阵。
通过由时间不稳定性分析得到的特征值谱(ωr,ωi),其中,ωr为扰动模态的扰动频率;ωi为扰动模态的不稳定性增长率。通过特征值谱可以分析基准流动的不稳定性、不稳定性增长率及不同扰动模态对应的频率和波数等特征,脉动压力边界条件则由N-S 方程推导得到的相容性方程确定。考虑到数值精度和收敛速度的要求,方程的离散采用了切比雪夫谱配置点法。关于相应边界条件的信息,本文参考Cheng 等[23]对孤立翼尖涡的局部LSA 所做的工作。稳定性分析中基准流动的速度场均通过自由来流速度U∞无量纲化。
2 翼尖涡特征值谱及模态特征
在进行线性稳定性分析时需要首先获取准确的基准流动,要求基准流动满足N-S 方程并具有一阶小量精度。为此本文采用将实验测量结果向方程解析解拟合的方法,对翼尖涡的切向与轴向速度型按照Q 涡模型进行最小二乘拟合,将实验结果拟合得到的Q 涡作为扰动方程中的基准流动[27]。以x/c=12、机翼攻角AOA=8°、Rec=0.84×105条件下的孤立涡为例,对实验测得的速度型作Batchelor 涡拟合,以此为基准流场进行时间稳定性分析得到的翼尖涡特征值谱如图3 所示。翼尖涡的时间稳定性特征值谱由3 种在复平面(ωr,ωi) 上不同位置的特征值组成。Mack[28]在1976 年针对边界层的时间模态OS 方程(Orr-Sommerfeld Equation)的特征值在复平面上分布位置的不同,将特征值分为A、S、P 族,并指出A、S、P 族分别对应变化剧烈的壁面来流模态、衰减模态和中心流动模态。观察到孤立翼尖涡的3 种不同特征值所对应的扰动模态与Mack 分类出的3 种不同特征值所对应的扰动模态具有相似的拓扑结构,因此此处将翼尖涡的次级扰动模态也相应地分为A、S、P 族[29]。
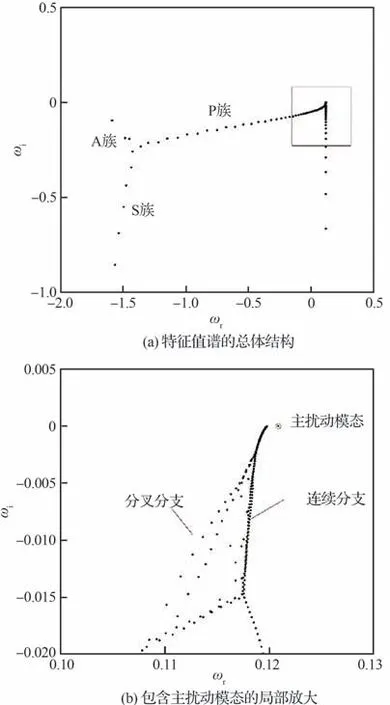
图3 x/c=12、AOA=8°、U∞=15 m/s 条件下孤立翼尖涡的特征值谱Fig.3 Eigenvalue spectrum of wingtip vortex at x/c=12,AOA=8°,U∞=15 m/s
在翼尖涡的稳定性分析中,将不稳定性放大率最大的模态称为主扰动模态,它被包含在P 族扰动模态中,具体位置如图3(b)所示。而在翼尖涡的不稳定扰动模态中,除主扰动模态外,还存在不稳定性放大率较小的模态,称为次级扰动模态。将P 族所在的特征值谱局部放大,此处的时间不稳定性特征值谱包含离散、连续、分叉3 个分支,如图3(b)所示。离散分支即为翼尖涡的主扰动模态。由于流场的扰动是不同频率和波数的扰动模态的叠加,研究次级扰动模态的特征及其演化规律是有积极意义的。与主扰动模态相比,次级扰动模态具有完全不同的扰动结构特征,研究其对翼尖涡不稳定性特征的影响有助于对翼尖涡失稳衰减的深入认知。
2.1 主扰动模态特征
主扰动模态对应图3 所示的特征值谱中虚部最接近正半平面的孤立点,其流向波数α=0.18,不稳定性放大率为ωi=−3.74×10−5。主扰动模态的物理含义为:对于α=0.18 的扰动,在翼尖涡经过长时间演化后,其他特征值点对应的扰动模态均随时间衰减殆尽,此时只有ωi=−3.74×10−5所对应的模态仍然主导着翼尖涡的扰动特征。
图4 显示了翼尖涡的主扰动模态在特征值谱的位置和模态横向速度分布,utr随着流向发展会发生周期旋转,它的几何结构与翼尖涡摇摆的第1 个POD 模态结构一致,是孤立翼尖涡摇摆发生的内在原因[12]。为了更好地比较次级扰动模态与主模态的几何特征,这里给出主模态的3 个坐标轴方向上的扰动速度分布,如图5 所示。对于离散分支的主扰动模态,它的横向速度波动要大于流向速度波动,且v′、w′均在涡核区域存在有较大的扰动幅值,而因为考虑m=−1 的情况,u′呈现出两瓣的结构,检验其他工况下流向截面的情况,均可得到相同的规律。需要注意的是,此处扰动模态的速度场波动u′、v′、w′均为无量纲参数。

图4 翼尖涡主扰动模态特征Fig.4 Characteristics of most unstable perturbation mode of wingtip vortex

图5 翼尖涡主扰动模态的各方向速度场波动Fig.5 Perturbation of velocity field of most unstable per‐turbation mode of wingtip vortex
2.2 P 族次级扰动模态特征
图6 显示了P 族次级扰动模态在特征值谱的位置和横向速度分布。值得注意的是,P 族次级扰动模态与主扰动模态具有相似的扰动结构,而主扰动模态因为具有更高的扰动频率从而在特征值谱中从P 族扰动模态中“分离”出来。为了更好地描述这种变化,引入相速度的概念,其表达式为
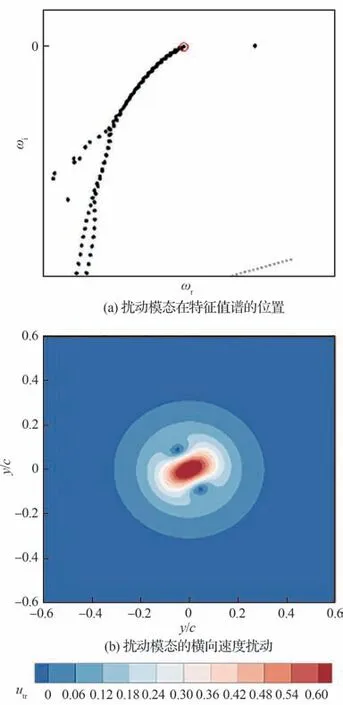
图6 翼尖涡P 族次级扰动模态特征Fig.6 Characteristics of Mode-P of wingtip vortex
相速度的物理意义在于表征扰动模态沿着流向的发展速度,除了翼尖涡的主扰动模态以外,翼尖涡的次级扰动模态的相速度均小于1。P族次级扰动模态具有和主扰动模态相似的扰动结构,而主扰动模态具有明显更高的不稳定性放大率和相速度,但是P 族的次级扰动模态却具有更高的横向速度扰动幅值,以此时的工况为例,主扰动模态的不稳定放大率ωi=−3.74×10−5,横向速度扰动峰值utrmax=0.707 118,而P 族次级扰动模态不稳定放大率ωi=−8.58×10−5,横向速度扰动峰值utrmax=0.741 941,这说明扰动的幅值和不稳定放大率并不存在必然联系,扰动幅值高并不能作为衡量主扰动模态的特征,不稳定放大率是由多方面的因素决定的。
图7 所示为P 族次级扰动模态在3 个方向上的扰动速度分布,次级扰动模态在横向的速度波动会大于主扰动模态的速度波动,且方向相反,这意味着P 族次级扰动模态会抑制主扰动模态带来的速度波动。同时,P 族次级扰动模态在流向上的速度扰动具有相似的结构,但是扰动的幅值较小,这反映了翼尖涡主扰动模态在流向发展上的特质,需要进一步从模态沿着流向的演化规律揭示翼尖涡主扰动模态不稳定性放大率最高的原因。

图7 翼尖涡P 族次级扰动模态的各方向速度场波动Fig.7 Perturbation of velocity field of Mode-P of wing‐tip vortex
无论是P 族次级扰动模态还是翼尖涡的主扰动模态,它们都有类似于Fabre 等[18]在2006 年定义的位移波(Displacement Wave)的结构,当叠加在基流上时,这种扰动的作用是增加一半涡核区域的涡度,减小另一半涡核区域的涡度,从而促进整个涡核的螺旋式位移。
2.3 A 族次级扰动模态特征
A 族次级扰动模态对应相速度cr较小而变化相对剧烈的壁面扰动模态。图8 显示出A 族次级扰动模态在特征值谱的位置以及其横向速度扰动分布。与P 族次级扰动模态相比,A 族次级扰动模态具有更小的扰动作用范围,横向扰动幅值较小且集中在涡核区域。
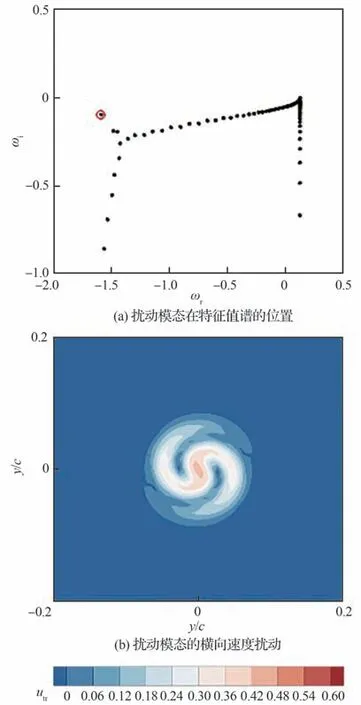
图8 翼尖涡A 族次级扰动模态特征Fig.8 Characteristics of Mode-A of wingtip vortex
图9所示为A族次级扰动模态各方向的速度扰动分布。A 族的次级扰动模态在横向的速度波动v′、w′具有多瓣的扰动结构特征,而流向的扰动幅值u′呈现出两瓣的结构特征。相比于横向速度扰动,A 族扰动模态在流向上具有较高的扰动幅值,这种扰动模态结构与Fabre 等[18]的涡核波动模态结构类似,这种扰动模态会在涡核内诱发出轴向运动,反作用于翼尖涡的基准流场,促进翼尖涡发生垂直于流向方向的旋转运动。

图9 翼尖涡A 族次级扰动模态的各方向速度场波动Fig.9 Perturbation of velocity field of Mode-A of wing‐tip vortex
2.4 S 族次级扰动模态特征
S 族次级扰动模态对应剪切区域外的自由来流扰动模态,其特征函数在无穷远场是振荡而非衰减的。图10 所示为S 族次级扰动模态在特征值谱的位置以及其横向速度扰动分布。尽管S 族次级扰动模态与A 族次级扰动模态具有相速度较小的扰动传播特点,但S 族次级扰动模态具有更高的横向速度扰动幅值,因此,对翼尖涡自身涡量变化的影响会更大。
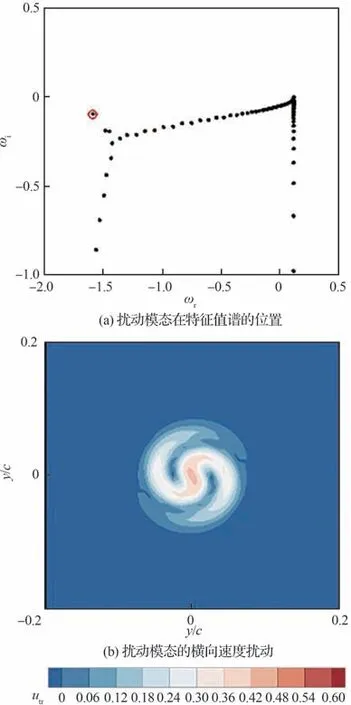
图10 翼尖涡S 族次级扰动模态特征Fig.10 Characteristics of Mode-S of wingtip vortex
图11 所示为S 族次级扰动模态各方向的速度扰动分布。S 族的次级扰动模态在横向的速度波动v′、w′具有多瓣的扰动结构特征以及更大的径向扰动波数,流向的扰动幅值u′呈现出多瓣的结构特征,且具有更高的扰动幅值。这种扰动模态结构与Fabre 等[18]的纯黏性模态结构类似,反映出黏性对翼尖涡速度场波动带来的影响。S 族次级扰动模态的扰动结构是与A 族次级扰动模态类似的中心螺旋扰动模态,不同的是具有更大的作用范围,随着周向波数的增加会逐渐发生螺旋线结构的延伸,且扰动会逐渐扩散到涡核区域。
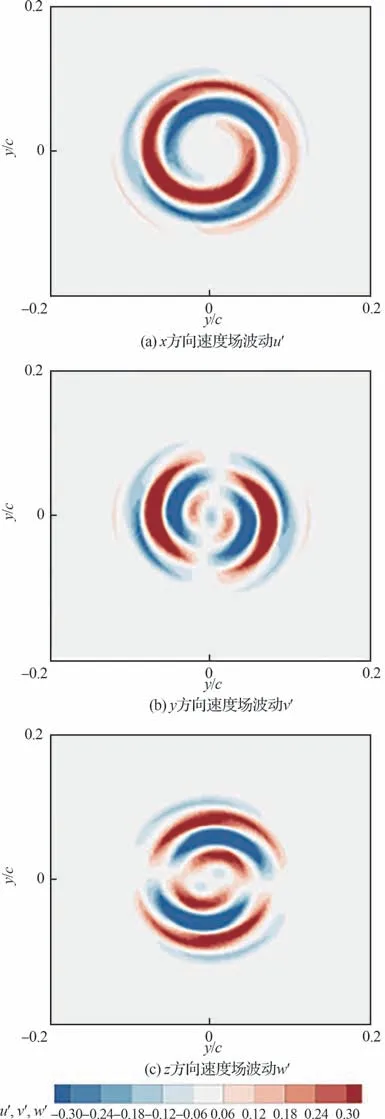
图11 翼尖涡S 族次级扰动模态的各方向速度场波动Fig.11 Perturbation of velocity field of Mode-S of wingtip vortex
综上所述,除主扰动模态以外,翼尖涡的次级扰动模态对整个翼尖涡的不稳定性发展起到一定的作用。次级扰动模态根据其在特征值谱的位置主要分为3 种不同的族群:P 族次级扰动模态,A 族次级扰动模态,S 族次级扰动模态。不同族群的次级扰动模态具有不同的成因和扰动结构,在同一流向截面下会对翼尖涡自身的运动带来不同的影响。由于翼尖涡不稳定性随流向发展变化剧烈,需要从整个流场的演化的角度研究不同族次级扰动模态的流向演化规律,从而进一步明确次级扰动模态对翼尖涡不稳定性特征的影响,这点将在第4 节详细阐述。
3 翼尖涡扰动模态的流向演化规律
3.1 翼尖涡不稳定性随流向的演化规律
在AOA=8°、Rec=0.84×105工况下,分别对x/c=4,8,12,16 这4 个流向位置的孤立翼尖涡进行时间不稳定性分析,提取每个流向截面的主扰动模态,在此基础上进行流向波数的扫略,得到扰动主模态的时间放大率ωi关于α的变化趋势,即不稳定性曲线,图12 显示了不同流向位置的不稳定性曲线,通过曲线顶点可以判断该工况下翼尖涡扰动的最大时间不稳定性增放大ωi及其对应的流向波数α。通过比较不同流向截面的不稳定性曲线可以得到翼尖涡不稳定性随流向的演化规律。随着流向波数的增大,翼尖涡的主扰动模态的不稳定性放大率总是先增大后减小,对于多数工况,流向波数α=0.18 时翼尖涡的不稳定性放大率最大,综合考虑α=0.18 是翼尖涡流场的整体最优解,在图12 中已经用黑色实线标出。同时,随着流向的演化,翼尖涡的不稳定性放大率在流场位置x/c=8 处会有一个不稳定性放大率的突跃,翼尖涡整体流场的不稳定性随着流向不断增加,增速随着流向逐步放缓。这说明翼尖涡流场早期形成的区域是不稳定性充分发展的区域,而翼尖涡的远场是翼尖涡不稳定性特征明显的区域。
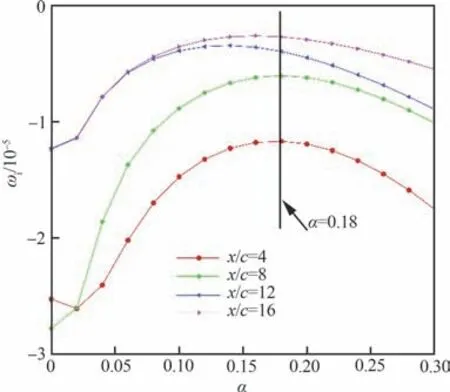
图12 在Rec=0.84×105、AOA=8°工况下不同流向截面的孤立翼尖涡的稳定性曲线Fig.12 Stability curves of wingtip vortex at different lo‐cations under at Rec=0.84×105,AOA=8°
图13 显示了孤立翼尖涡的特征值谱的流向演化规律,不同族的翼尖涡次级扰动模态随着流向发展的变化轨迹是不同的。对于翼尖涡的主扰动模态和P 族次级扰动模态,随着流向位置的变化主要体现在不稳定性放大率ωi,而其相速度cr几乎保持不变,这说明P 族次级扰动模态和主扰动模态随着流向的传播ωi速度无明显变化,而在不同的流向截面处,总有可以被激发的主扰动模态,它随着流向的传播速度甚至超过流场速度,主导着翼尖涡流场的变化。对A 族次级扰动模态和S 族次级扰动模态,随流向的变发展均有明显的速度场波动变化,且在不稳定性增长率ωi和扰动频率ωr均随着流向不断增加,而ωr的增速远超过ωi,同时A 族次级扰动模态和S 族次级扰动模态的相速度在翼尖涡的所有扰动模态里均较小,而随着流向的发展,2 种模态的相速度均逐步增加,随着流向的传播速度逐渐加快,这说明A 族次级扰动模态和S 族次级扰动模态在翼尖涡的远场区域具有更强的扰动影响。
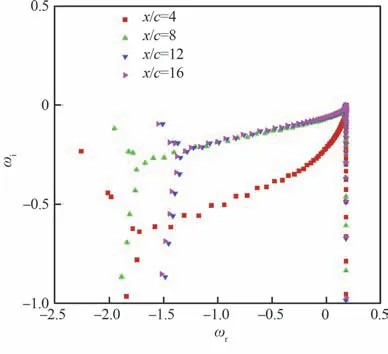
图13 在Rec=0.84×105、AOA=8°工况下不同流向截面的孤立翼尖涡的特征值谱Fig.13 Eigenvalue spectrum of wingtip vortex at differ‐ent flow locations at Rec=0.84×105,AOA=8°
综上所述,翼尖涡的不稳定性特征的流向演化规律是不稳定性放大率逐渐增大,而增速逐渐放缓。同时,在Rec=0.84×105、AOA=8°工况下,孤立翼尖涡的主扰动模态和次级扰动模态上具有不同的流向演化规律。尽管在不同的流向位置翼尖涡的不稳定放大率不同,但几乎都在α=0.18 的位置处于最大值,也就是,在α=0.18 的条件下,翼尖涡的不稳定特征最为明显。基于此结论,接下来的模态演化规律讨论默认在α=0.18 的条件下进行。
3.2 翼尖涡主扰动模态和P 族次级扰动模态的流向演化规律
通过2.1、2.2 节的研究可知,翼尖涡的P 族次级扰动模态和主扰动模态之间的结构是相似的,且P 族次级扰动模态具有更高的横向速度波动。而主扰动模态具有更高的相速度,即随着流向的传播速度较快。结合第3.1 节翼尖涡不稳定性演化规律的研究,将翼尖涡主扰动模态所在的区域局部放大,观察翼尖涡主扰动模态和翼尖涡P 族次级扰动模态的演化规律,如图14、图15所示。
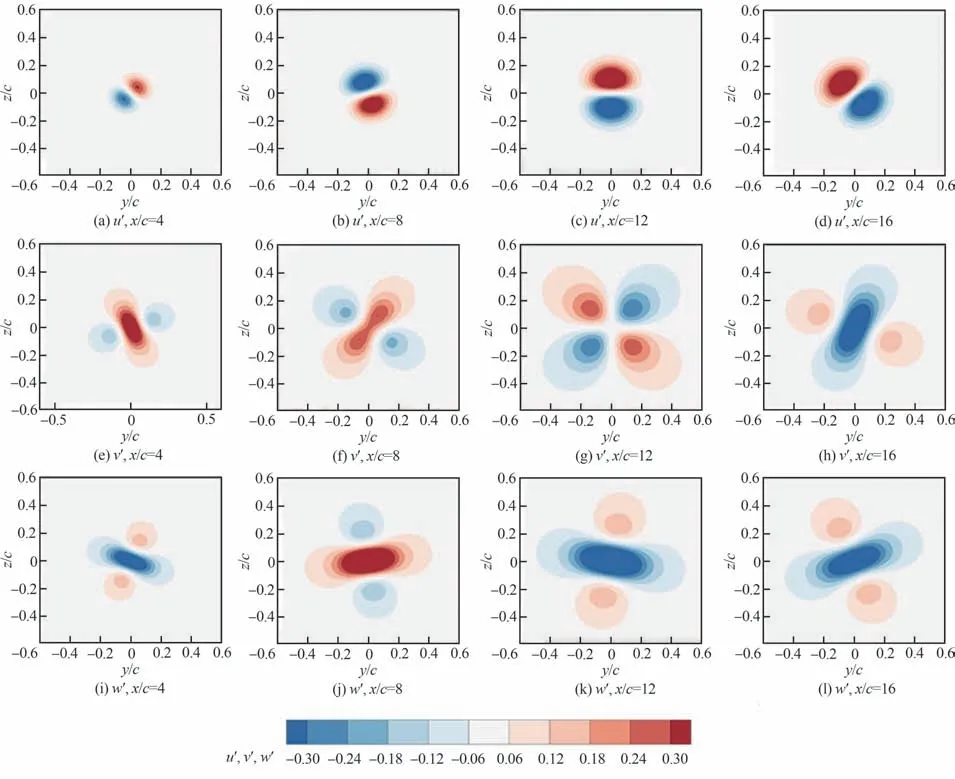
图14 在Rec=0.84×105、AOA=8°工况下不同流向截面的孤立翼尖涡的主扰动模态特征Fig.14 Characteristics of primary mode of isolated wingtip vortex at different flow locations at Rec=0.84×105,AOA=8°
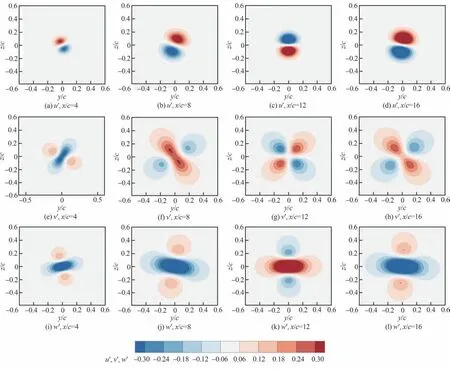
图15 在Rec=0.84×105、AOA=8°工况下不同流向截面的孤立翼尖涡的P 族次级扰动模态特征Fig.15 Characteristics of Mode-P of isolated wingtip vortex at different flow locations at Rec=0.84×105,AOA=8°
图14 展示出翼尖涡主扰动模态随流向的演化规律,翼尖涡主扰动模态的流向速度波动随着流向的发展始终保持着两瓣式的结构并不断旋转,同时,扰动的幅值和范围都在随着流向不断增长,这促进了翼尖涡摇摆运动的加剧。进一步地,观察翼尖涡的主扰动模态在横向截面上的速度扰动,在翼尖涡近场区域,翼尖涡主扰动模态的横向速度扰动幅值v′、w′大于流向速度扰动幅值u′,翼尖涡的主扰动模态作用集中于翼尖涡的横向形变。而随着流向的发展,翼尖涡的主扰动模态的流向速度扰动幅值u′会远远大于v′、w′,主扰动模态逆着涡旋方向旋转并沿着流向发展,进而促进整个涡核的螺旋式位移。
图15 展示出翼尖涡的P 族次级扰动模态的流向演化规律,P 族次级扰动模态的流向演化规律于翼尖涡主扰动模态类似,而在流向的发展演化中,P 族次级扰动模态在各个方向的扰动往往与翼尖涡主扰动模态在同一方向上带来的扰动相反,这说明在流向的发展演化中,P 族次级扰动模态和翼尖涡主扰动模态叠加到基流上时,P 族次级扰动模态往往会抑制翼尖涡主扰动模态带来的种种波动,以x/c=12 的流向截面为例,P 族次级扰动模态与翼尖涡主扰动模态在各个方向上带来的速度波动几乎完全相反。同时,当翼尖涡的主扰动模态在某个方向的速度扰动增大时,相应的P 族次级扰动模态也会增大,这一点在流向速度扰动上显得尤为明显,在x/c=4 的流向位置上,翼尖涡的主模态的流向扰动峰值是0.325 6,而P 族次级扰动模态的流向扰动峰值是0.310 7,而当扰动模态发展到x/c=16 位置时,翼尖涡的主扰动模态的流向扰动峰值是0.530 4,而翼尖涡的次级扰动模态的流向扰动峰值是0.646 7,高于翼尖涡的主扰动模态,在此时的流向截面,P 族的次级扰动模态会带来更大的翼尖涡螺旋式位移。因此,翼尖涡的P 族次级扰动模态在翼尖涡的流向发展过程中会对翼尖涡的摇摆运动带来促进作用,而这种作用效果会随着流向的发展不断的变大。
3.3 翼尖涡A 族次级扰动模态和S 族次级扰动模态的流向演化规律
通过2.3、2.4 节可知,翼尖涡的S 族次级扰动模态和A 族次级扰动模态都具有相速度较小的特征,扰动的传播速度远远落后于流向的发展速度,并随着流向的发展渐渐消逝,同时A 族次级扰动模态和S 族次级扰动模态具有更小的作用范围。因为A 族次级扰动模态和S 族次级扰动模态的成因不同,研究其演化规律反映出孤立翼尖涡不同的物理特征对其翼尖涡不稳定性的影响。A 族次级扰动模态反映了黏性对翼尖涡速度场的影响,而S 族次级扰动模态反映了翼尖涡的瞬态增长特性。结合3.1 节对翼尖涡不稳定性演化规律的研究,观察翼尖涡A 族次级扰动模态和S 族次级扰动模态的演化规律,如图16、图17所示。

图16 在Rec=0.84×105、AOA=8°工况下不同流向截面的孤立翼尖涡的A 族次级扰动模态特征Fig.16 Characteristics of Mode-A of isolated wingtip vortex at different flow locations at Rec=0.84×105,AOA=8°

图17 在Rec=0.84×105、AOA=8°工况下不同流向截面的孤立翼尖涡的S 族次级扰动模态特征Fig.17 Characteristics of Mode-S of isolated wingtip vortex at different flow locations at Rec=0.84×105,AOA=8°
图16 展示出翼尖涡A 族次级扰动模态随流向的演化规律。在2.3 节已经指出,翼尖涡的A族次级扰动模态在流向速度扰动上的扰动较高,与之相比,A 族次级扰动模态在横向截面上的扰动较小。而随着流向的演化发展,A 族次级扰动模态依然保持这种特征,流向的扰动幅值随着流向的发展逐渐增大且影响范围更广,这种流向的扰动呈螺旋状围绕着涡核,并沿着流向逐渐扩散到整个涡核,作用于整个翼尖涡的螺旋式位移。同时,A 族次级扰动模态的横向速度随着流向变动较为复杂,不仅表现在作用方向上的旋转变化,而且表现在作用范围的不规则变化。但是由于横向速度扰动的幅值和幅值的增速远远小于流向扰动幅值,因此A 族次级扰动模态的横向扰动对翼尖涡的作用效果较为有限。
图17 展示了翼尖涡S 族次级扰动模态随流向的演化规律。S 族次级扰动模态的流向扰动一开始围绕在涡核的外侧,流向扰动幅值较小,在流向位置x/c=4 处,流向扰动峰值为0.523 18。而随着翼尖涡的发展演化,S 族次级扰动模态逐渐深入到翼尖涡涡核内部,覆盖住整个涡核,流向速度扰动幅值会逐渐在增大,在流向位置x/c=4 处,流向扰动峰值为0.872 30。而这种变化对于S 族次级扰动模态的横向扰动则是不明显的,以y方向的横向扰动v′为例,在x/c=4 处,扰动幅值为0.580 37,而在x/c=16 处,扰动幅值为0.572 63,并没有明显波动。这从侧面说明S 还与扰动模态相对于涡核的作用范围有关:扰动模态覆盖涡核的范围越大,其流向扰动的幅值变化越剧烈,会加剧对翼尖涡不稳定性特征的影响。
3.4 翼尖涡扰动模态的能量增长
进一步地,引入能量增长的观点描述各族次级扰动模态的特征,指定时间内的初始扰动的最优能量放大G(t)的计算公式[30]为
式中:q0为初始扰动;q(t)为扰动随时间的演化量;Λ为由特征值ω构成的特征值矩阵,该矩阵代表不同的初始条件下可以产生的最大可能的能量放大。在线性稳定性分析中,这种扰动的放大是根据翼尖涡的最不稳定模态来确定的,算子的范数与不稳定放大率最大的主扰动模态直接相关,最优能量扰动的放大率可以写为
式中:ωi‐max为主扰动模态的不稳定性放大率,因为主扰动模态在整个特征值谱中具有更大的扰动能量放大率。
在翼尖涡的次级扰动模态中,除了主扰动模态以外,P 族次级扰动模态和S 族次级扰动模态同样具有较高的不稳定性放大率。2018 年,Ed‐strand 等[3]研究指出,对于基于不稳定性模态的翼尖涡主动控制,或者说激发翼尖涡扰动模态促进翼尖涡速度场变化的主动控制理论而言,扰动模态的结构是不可忽略的因素。比较不同流向截面处扰动模态结构相差较大的主扰动模态和S族次级扰动模态的能量增长随时间的演化规律,如图18 所示。随着翼尖涡的流向演化,主扰动模态和S 族次级扰动模态的扰动能量增长率逐渐增大,尽管主扰动模态的能量增长始终占主导地位,S 族次级扰动模态随着流向演化具有更高的增长速度,与主扰动模态的能量差值随着流向演化不断缩小。

图18 主扰动模态和S 族次级扰动模态在不同流向截面处的扰动能量增长(Rec=0.84×105)Fig.18 Perturbation energy growth of primary pertur‐bation mode and mode-S at different flow sec‐tions(Rec=0.84×105)
对于孤立翼尖涡,其典型两瓣式结构的主扰动模态虽然穿透了涡核边界覆盖整个翼尖涡涡核,但是其扰动切向波数仅为m=−1,Xiang[20]、程泽鹏[20-21]等通过对翼尖涡的稳定性分析,得出较低的切向波数是主扰动模态对翼尖涡的干扰十分低效的原因所在,因此主扰动模态总是处于临界不稳定状态。相比于主扰动模态,S 族次级扰动模态具有更高的切向波数,同时,扰动模态本身也穿透了涡核边界并覆盖整个翼尖涡涡核。从能量角度,S族次级扰动模态的扰动能量增长与主扰动模态的差距随着流向演化逐渐缩小。尽管S 族次级扰动模态随着流向的发展会更快地耗散[31],但通过模态的激发,S 族次级扰动模态能够随着流向发展进一步增强,同时保持高切向波数和大作用范围的特点,有理由相信基于S 族次级扰动模态的翼尖涡主动控制相比于传统的基于主扰动模态的翼尖涡主动控制是更具有吸引力的策略。关于翼尖涡扰动模态的激发,Edstrand 等[3]曾经做过相应的数值模拟,取得了一定的成果,但还需要进一步验证如何通过实验手段激发S 族次级扰动模态的速度场波动,从而促进翼尖涡整体的失稳衰减。
4 结论
通过SPIV 实验获得不同流向截面的孤立翼尖涡流场,通过对实验数据进行拟合计算得到基准流动,在此基础上开展时间不稳定性分析,得到如下主要结论:
1)孤立翼尖涡的扰动模态可以根据其在特征值谱的位置分为主扰动模态、P 族次级扰动模态、A 族次级扰动模态、S 族次级扰动模态4 种。主扰动模态在翼尖涡不稳定性的发展中起主导作用,P 族次级扰动模态具有与主扰动模态相似的扰动结构,共同促进翼尖涡涡核的摇摆运动,A族次级扰动模态的扰动结构反映出黏性对翼尖涡运动的影响,会诱发翼尖涡涡核处的周向运动,S 族次级扰动模态的扰动结构具有更高的切向波数,随着周向波数的增加会逐渐发生螺旋线结构的延伸并扩大扰动的作用范围。
2)分别给出不同族的扰动模态随流向的演化规律,翼尖涡的主扰动模态和P 族扰动模态沿流向发生旋转,并且扰动幅值随着流向逐渐放大,A 族次级扰动模态的流向演化规律主要集中在流向速度上,表现为幅值的增加和作用范围的增大,S 族次级扰动模态随着流向会逐渐覆盖住整个涡核,带来较大的流向速度波动。
3)从基于不稳定性思路的翼尖涡主动控制角度讨论了翼尖涡次级扰动模态的作用,描述了不同翼尖涡扰动模态的扰动能量随流向的演化规律。翼尖涡的主扰动模态具有最高的能量增长,但由于其低切向波数的结构,对翼尖涡的扰动较低效。而S 族扰动模态因为具有更高的切向波数和较大的扰动能量增长,基于S 族次级扰动模态的翼尖涡主动控制是一种更具有吸引力的策略。

