改进速度障碍法的无人机局部路径规划算法

郭华，郭小和

南昌航空大学 飞行器工程学院，南昌 330000

随着航空技术的发展，无人机在现代战争和民用领域中扮演着越来越重要的角色，应用领域不断扩大，航迹规划作为无人机任务规划的核心，是无人机完成任务的关键步骤［1-2］。其中的关键为躲避动态障碍物或威胁需进行的局部路径规划算法，要求具有计算量小、实时性好的特点［3］。常见的局部路径规划算法主要有人工势场法、导引法、速度障碍法、基于机器学习的避障规划算法等［4-5］。人工势场算法虽然计算量小、应答时间短，但是存在不能准确到达目标点、飞行路径波动、路径不可飞等问题，许多学者对人工势场法进行了优化设计［6-8］。导引法借鉴导弹制导律，将导引方法应用于避障算法，但是此算法没有很好考虑无人机避障完成后的运动，也不能很好解决多障碍物入侵问题［9］。常见的机器学习算法有神经网络、强化学习与深度强化学习等，但此类算法复杂耗时。此外一些智能算法，比如遗传算法、粒子群算法和模拟退火算法等，此类算法计算量偏大，多用于基于已知环境信息的无人机全局路径规划之中［10-12］。速度障碍法最开始用于解决移动机器人的自主避障问题［13-14］，现在广泛应用于无人艇和无人机的避障与航迹规划算法中，Durand 和Barnier［15］最早在无人机避免与其他无人机发生冲突的过程中引入速度障碍法。目前很多学者通过降维思想来处理三维空间的路径避障问题，文献［16］通过降维处理避碰障碍锥，利用比例导引法完成三维避碰。文献［17-18］基于平面几何优化处理和最少机动的原则，建立了航空器之间的飞行冲突解脱和航迹恢复模型，并且考虑了无人机在冲突解脱后的航迹恢复问题。文献［19］提出基于时间速度障碍法，为飞行器提供了更大范围的可选避障速度向量范围。文献［20］考虑了二维环境下的动态障碍物运动的不确定性，提高了水下机器人在实际运行中的避撞稳定性。文献［21］提出一种基于三维空间障碍球冠的动态不确定速度障碍模型，并将三维动态不确定无人机自主避障算法应用于Pythagorean Hodograph（PH）曲线的在线路径当中。文献［22-23］将速度障碍法运用到多机同构系统躲避机动障碍物和三维空间内单机躲避障碍物之中。

上述三维速度障碍法为保证安全避障，安全避障距离普遍偏大，降低了原规划航迹的使用率。本文通过建立三维空间障碍物运动不确定性速度障碍锥，分析空间几何模型，求解无人机在三维空间中自主避障的最小速度矢量偏转角，并引入自适应威胁距离，提高了原规划航迹的使用率。

1 三维速度障碍法原理

传统速度障碍法往往只考虑二维平面，根据空中交通管制规则，无人机与障碍物之间应保持一定的安全距离［24］，若将飞机视为质点，障碍物进行相应“膨胀”，则无人机的动态避障过程可简化为一个质点躲避膨胀圆的过程。速度障碍（Velocity Obstacle，VO）是在无人机的速度空间内生成一个圆锥形障碍区间，只要相对速度矢量在锥形区域之外，在将来的一段时间内无人机都不会与障碍物发生碰撞。

在三维空间中，假设无人机的辐射半径为Ru，某动态威胁障碍物的辐射半径为Ro。某时刻无人机与障碍物的位置分别为Pu、Po；无人机速度矢量为Vu；障碍物速度矢量为Vo；无人机的位姿信息(Pu，Vu)和障碍物的位姿信息(Po，Vo)可由式（1）～式（4）表示。

式中：vu、vo分别为无人机与障碍物的速度矢量大小；θu、φu和θo、φo分别为无人机与障碍物的速度矢量方向角（θ为俯仰角，φ为偏航角）。

如图1 所示，以Po为球心，R为半径作球体，以Pu为顶点作锥体与球Po相切，球体可以较好的模拟飞机等具有机动性较强的动态障碍物。其中Vuo为二者相对矢量速度；相对速度的大小为vuo；d为无人机与障碍物之间的欧几里得距离。若矢量Vuo末端在三维空间速度障碍锥内，则动态障碍物对无人机存在威胁。

图1 三维速度障碍法原理Fig.1 Schematic of 3D velocity obstacle method

通常情况下，我们更希望直接通过无人机的速度矢量Vu来判断障碍物与飞机是否存在飞行冲突。将Pu和Po沿向量Vo的方向平移距离‖VoΔt‖，得到Qu、Qo，如式（8）和式（9）所示；Δt为一个单位时间间隔。以Qo为球心、R为半径作球体，建立基于无人机速度矢量Vu的三维空间速度障碍锥模型，如图2 所示。如果Vu的矢量末端在锥体区域内，则障碍物对无人机产生威胁。

图2 三维空间速度障碍锥Fig.2 3D spatial velocity obstacle cone

障碍物对无人机是否造成威胁，还可以通过比较角度α0与α的大小来判定，其中α0为空间速度障碍锥的半顶角；α为相对速度Vuo与空间障碍锥线之间的夹角。若α>α0，障碍物不具有威胁性；若α<α0，障碍物具有威胁性。

2 速度障碍法的改进

2.1 安全距离

无人机的局部路径避障规划过程是在传感器探测到障碍物的尺寸、位置和速度等信息基础上进行的，由于传感器精度问题，可能导致探测到的障碍物信息存在偏差，并且速度障碍法在描述障碍物的信息时采用确定的值，这就可能导致发生碰撞。除此之外，速度障碍法的速度在周期内被认为是不发生变化的，直到下一刻才发生变化，所以速度障碍法要求传感器的刷新频率非常高。由此引入安全距离Rsafe，使膨胀半径再次增大，可提高无人机安全性裕度，此时膨胀半径可优化为R1，如式（12）所示：

2.2 自适应威胁距离

传统速度障碍法存在避障保守的问题，障碍物一旦位于无人机传感器探测范围内，无人机便开始冲突探测过程，若发现威胁便立刻采取避障措施。为消除无人机的这种保守避障策略，避免无人机在非必要情况下提前脱离原路径，引入自适应威胁距离dsafe。当无人机与障碍物之间的相对距离大于威胁距离时，无人机仍以当前速度飞行；相对距离小于或者等于威胁距离时，才开始采取动态避险策略。

经算法计算及结果分析，定义自适应威胁距离dsafe，如式（13）所示。dsafe的数值设定应与无人机、障碍物的速度和辐射半径等相关，dsafe的设定不宜过小，需要保证无人机的航向调整幅度满足无人机本身的约束条件，dsafe的设定可以提高原航迹的利用率。

假设无人机探测到危险到开始避障的时间间隔为tm，tm是无人机以当前速度继续飞行的最大时间，可由式（14）计算得出：

2.3 障碍物动态不确定性处理

无人机执行任务时，需要考虑无人机自身携带的障碍物感知模块在感知动静障碍物时存在一定的测量误差，以及感知到的动态威胁障碍物具有一定机动性等情况。若无人机探测到障碍物速度Vo，且该障碍物存在最大动态不确定度ε，如图3 所示，以Qu为球心，可以确定一个半径为r的机动球，结合机动球截面图，其中A、B两点为临界机动点，设Qu点到AB线段的最短距离为dmin，半径r可由式（17）表示。

图3 机动球Fig.3 Motive ball

在初始三维空间速度障碍的基础上建立三维空间不确定速度障碍锥，如图4 所示，母线l1、l2与机动球相切，此时膨胀圆半径可由R1更新为R2，由式（18）表示。

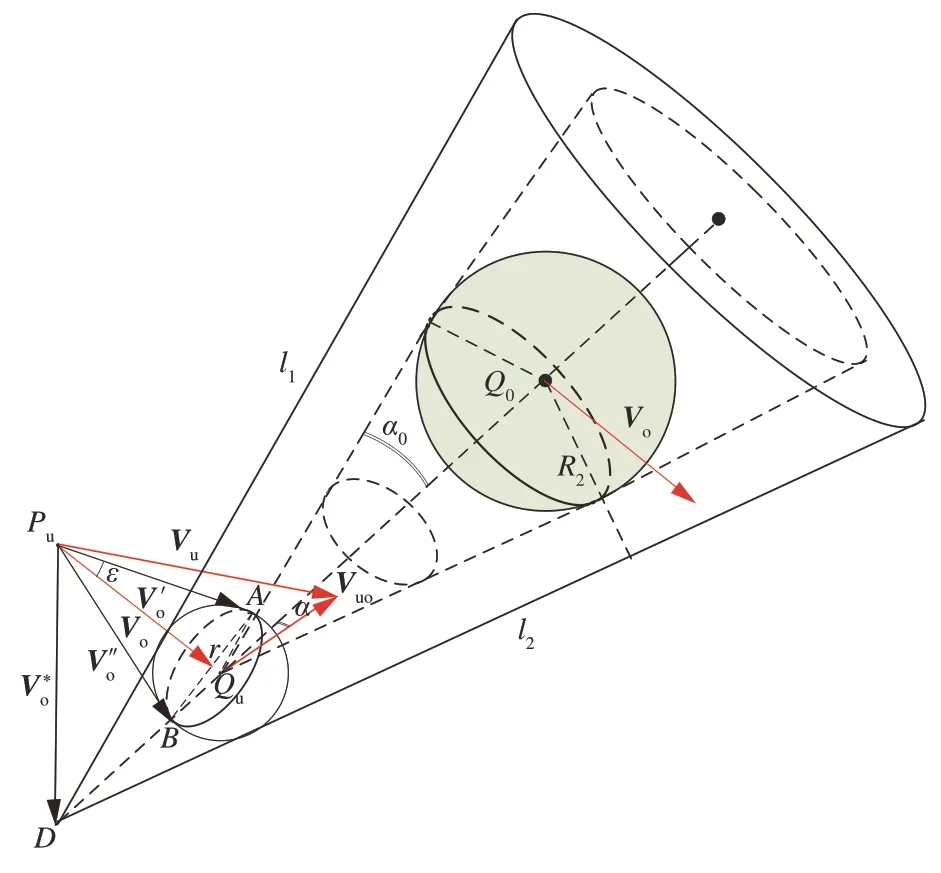
图4 考虑障碍物机动性的速度障碍锥Fig.4 Velocity barrier cone considering obstacle maneuverability

假设空间障碍锥轴线上有一单位向量n，圆锥体顶点D在轴线的延长线上，D点位置可由式（19）～式（21）得出：

3 无人机避障模型

3.1 冲突解脱

无人机在躲避威胁障碍物时，保持速度矢量Vu的大小不变，只改变速度矢量Vu的方向角。为方便研究Vu的偏转方向，以Pu为球心、vu为半径作球体，该球体称为速度球，如图5 所示，其阴影球冠为速度球与空间障碍锥的相交部分。无人机要实现避障，需将Vu的末端偏转出阴影球冠区域。在无人机求解期望速度模型图中，表示无人机的理想期望速度；相对应的期望相对速度分别表示为；E和F为无人机避障的临界状态点。

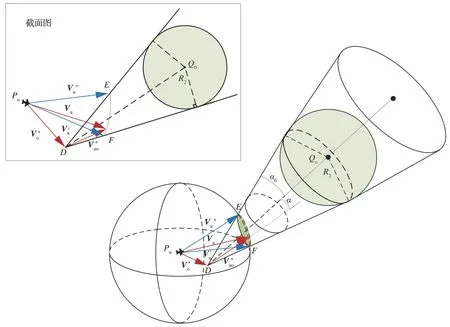
图5 无人机求解期望速度模型Fig.5 Solving expected velocity model for UAVs

通过式（24）～式（26）可以求解出x、y、z的值，进而确定单位向量m。

按照式（24）～式（30）计算方法同样可以求得无人机避障临界点E。通过求解期望矢量速度，进而可得无人机期望速度矢量的方向角为和，如式（31）～式（33）所示：

3.2 航迹恢复

理想状态下，无人机躲避障碍物以后，无人机要逐渐恢复到全局路径上进入正常飞行状态，如图6 所示。为了避免无人机的连续机动而增加风险，采取无人机仍以当前速度飞行，直至无人机与障碍物之间的距离开始增大，再改变航向角的策略。

图6 理想航迹恢复Fig.6 Ideal track recovery

4 仿真实验与分析

根据以上对改进速度障碍法的设计和分析，基于改进速度障碍法的无人机避障步骤如图7 所示。无人机提取自身与障碍物信息后，建立考虑障碍物机动性的速度障碍模型，进行冲突探测，若障碍物具有威胁，为避免无人机保守避障，无人机需继续以当前速度飞行一段时间后再改变速度矢量方向角进行避障；当无人机开始远离障碍物时，无人机可重新调整飞行方向，使无人机朝目标点飞行。

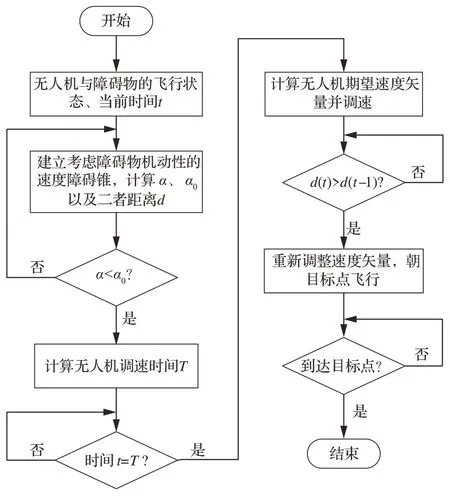
图7 基于改进速度障碍法的无人机避障流程图Fig.7 Flow chart of UAV obstacle avoidance based on improved speed obstacle method

采用MATLAB 软件进行仿真实验。首先设置一些基本初始参数：无人机的任务起点坐标(0，0，0) m；终点坐标(1 000，800，200) m；无人机速度大小vu=20 m/s；无人机辐射半径Ru=25 m；障碍物辐射半径Ro=15 m；安全距离Rsafe=8 m；传感器探测范围dsensor=600 m。为了验证算法的有效性和适用性，设定了3种场景，分别为无人机与障碍物对遇、追击及交叉，依次对应表1的3种场景。

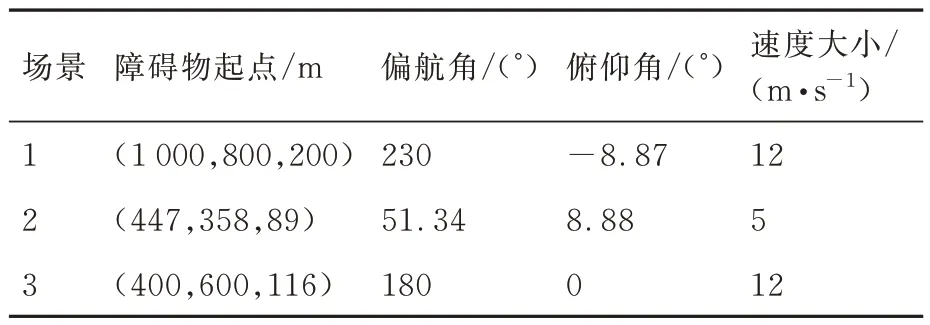
表1 障碍物初始条件参数Table 1 Obstacle initial condition parameters

4.1 机动性障碍物避障

为验证考虑障碍物机动性的避障算法的有效性，假设机动性障碍物的速度方向角的最大不确定度ε=10°，针对表1 所示的3 种场景，通过算法计算，不管是否考虑障碍物的机动性，3 种情景下α始终小于α0，即障碍物具有威胁性，表2 和表3 分别记录了考虑障碍物机动性与未考虑障碍物机动性的无人机避障过程的相关参数。

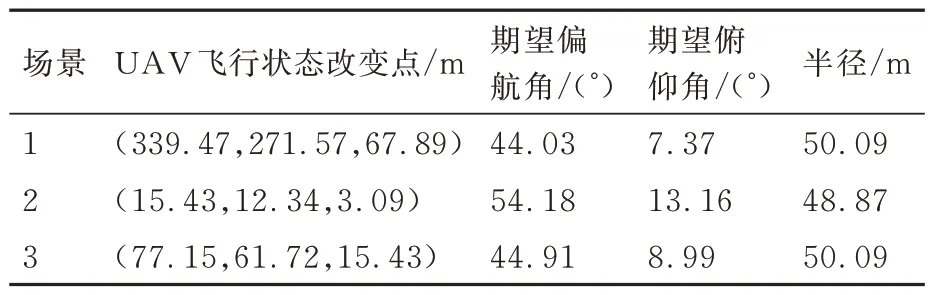
表2 考虑障碍物机动性的无人机避障过程相关参数Table 2 Parameters related to UAV obstacle avoidance process considering obstacle maneuverability

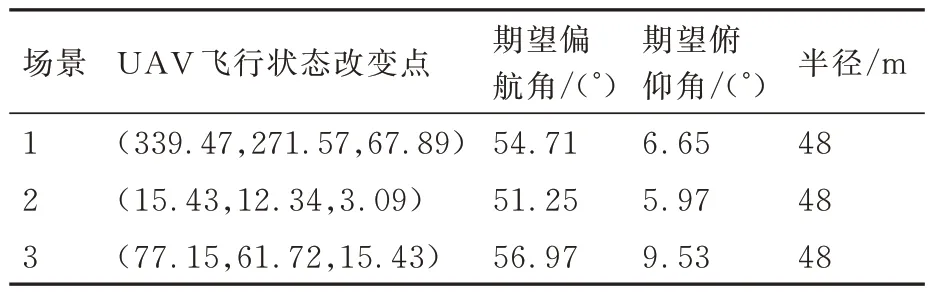
表3 未考虑障碍物机动性的无人机避障过程相关参数Table 3 Parameters related to UAV obstacle avoidance pro⁃cess without considering obstacle maneuverability

图8（a）和图8（b）展示了场景1 下无人机与障碍物的对遇运动过程（蓝色圆圈代表无人机运动轨迹，红色圆圈代表障碍物运动轨迹），可以看出无人机对障碍物都进行了躲避，并达到任务终点。结合表2 和表3，在考虑障碍物机动性的情况下，膨胀辐射半径为50.09 m，无人机在位置（339.47，271.57，67.89）m 处开始改变速度矢量，偏航角和俯仰角分别调整为44.03°和7.37°；在不考虑障碍物机动性的情况下，辐射半径为48 m，无人机在相同位置调整方向角，偏航角和俯仰角分别调整为54.71°和6.65°。图8（c）表示无人机与障碍物之间的距离变化，在考虑障碍物机动性二者达到的最近距离为56.262 7 m，大于对应的膨胀半径，二者没有发生碰撞；而在不考虑障碍物机动性的情况下，二者之间的最近距离为14.913 9 m，小于对应膨胀半径，说明无人机与障碍物发生了碰撞，避障失败。图8（d）记录无人机运动过程中俯仰角与偏航角的变化。

图8 场景1 实验仿真结果Fig.8 Experimental simulation results for Scenario 1

同理分析图9 和图10，无人机采用考虑动态障碍物机动性的算法，可在场景2 和场景3 中顺利完成避障过程，且无人机的偏航角度与俯仰角度都满足无人机的自身约束条件。

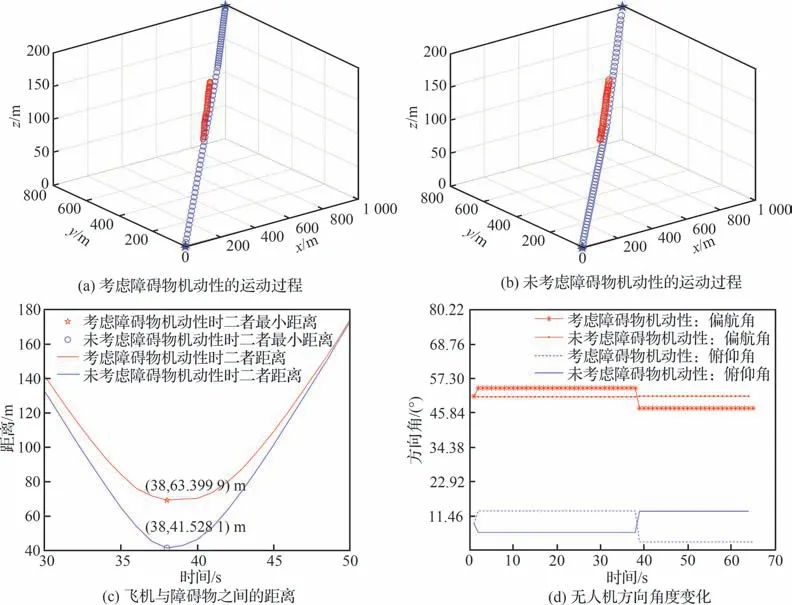
图9 场景2 实验仿真结果Fig.9 Experimental simulation results for Scenario 2

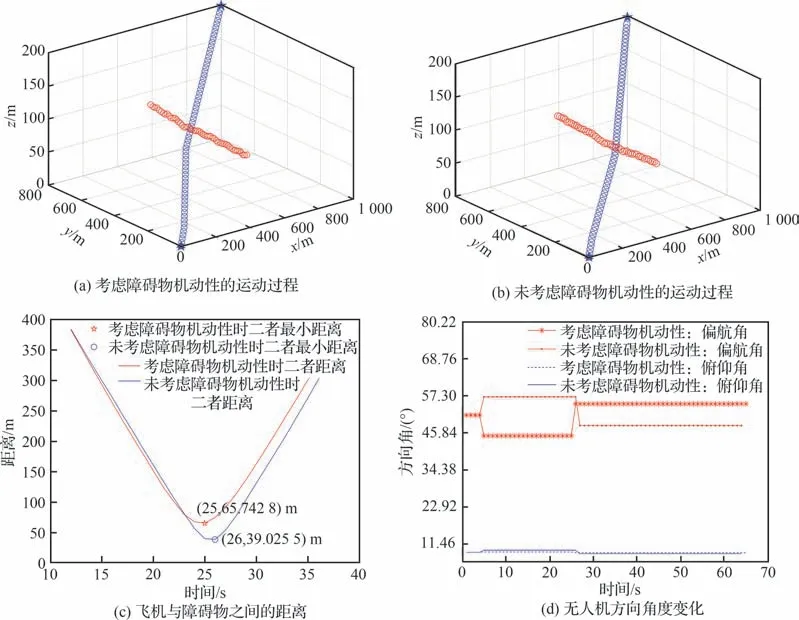
图10 场景3 实验仿真结果Fig.10 Experimental simulation results for Scenario 3

4.2 引入自适应威胁距离的机动性障碍物避障

为验证自适应威胁距离对无人机避障的影响，在考虑动态障碍物机动性的前提下，进行前文中提到的3 种相同场景的仿真实验。

通过表4 中的相关参数可知，在避障算法中引入威胁距离，无人机同样完成了对机动性障碍物的躲避。通过对比表2 与表4 中的UAV 飞行状态改变点的坐标值，可以看出自适应威胁距离的引入，无人机推迟了飞行状态的调整，进而提高了原飞行路径的利用率。图11 记录了无人机在3 种情景下的偏航角与俯仰角的变化过程，均能满足无人机自身的约束条件。

表4 考虑障碍物机动性并引入威胁距离的无人机避障过程相关参数Table 4 Relevant parameters of UAV obstacle avoid⁃ance process considering obstacle maneuver⁃ability but not threat distance m

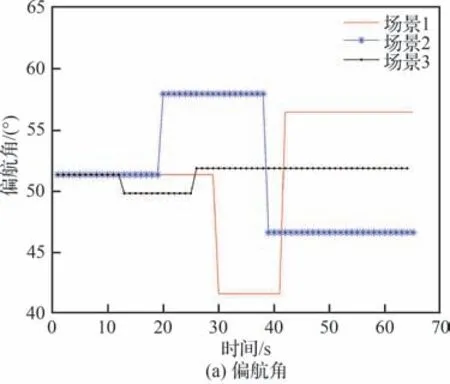
图11 无人机方向角变化Fig.11 Change of UAV direction angle

通过分析图8～图11 并结合仿真计算时间，可得3 种场景下的算法求解耗时、飞行解脱耗时等指标的对比仿真结果如表5～表7 所示，结果表明，虽然引入威胁距离前后的速度障碍算法在3 种场景下的求解耗时均在0.008 s 左右，但引入威胁距离后的优化速度障碍法，由于无人机在保证安全距离的前提下推迟了飞行状态的调整，在距离机动障碍物更近的情况下才开始规避，所以在飞行冲突解脱过程中耗时更短，提高了机动障碍规避的时效性。

表5 场景1 避障算法时效性对比Table 5 Comparison of timeliness of obstacle avoid⁃ance algorithms in Scenario 1

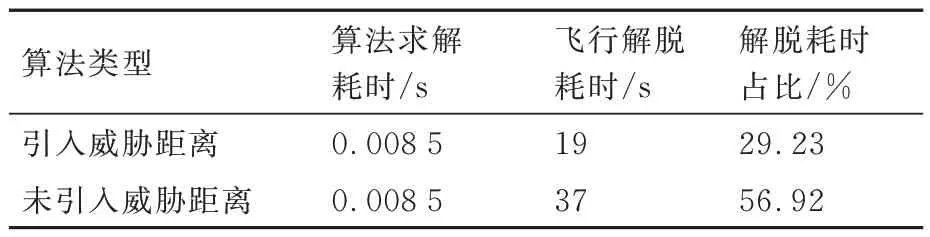
表6 场景2 避障算法时效性对比Table 6 Comparison of timeliness of obstacle avoid⁃ance algorithms in Scenario 2

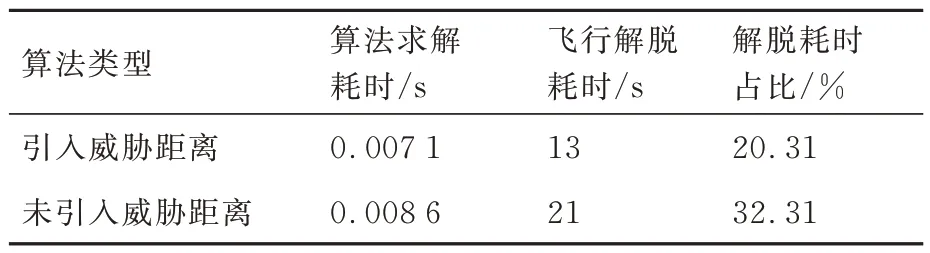
表7 场景3 避障算法时效性对比Table 7 Comparison of timeliness of obstacle avoid⁃ance algorithms in Scenario 3

5 结论

针对无人机基于复杂环境感知进行局部路径再规划的实时与安全性问题，提出一种基于改进速度障碍法的局部路径避障规划算法，算例仿真结果表明：

1）建立动态障碍物的三维速度障碍模型，将机动性动态障碍物在速度空间中的运动不确定转化为位置不确定，克服了传统速度障碍法仅能对匀速障碍物实现良好避障的缺点，提高了避障能力，保证了避障机体的飞行安全。

2）在避障算法中定义和引入自适应威胁距离，保证无人机避障安全性的同时也为无人机提供了更大范围的可选择避障速度向量范围，避免无人机提前脱离任务路径，提高了原航迹的利用率，且算法计算效率满足机动障碍规避的时效性需求。