拦截机动目标的信赖域策略优化制导算法

陈文雪，高长生，荆武兴

哈尔滨工业大学 航天学院，哈尔滨 150001

针对高速性、机动性的临近空间目标拦截制导问题是目前单枚弹道导弹防御中的一个研究热点及难点问题。近些年来，随着航天领域制导技术的发展，古典导引律、现代导引律均得到了快速发展。古典制导控制方法中，比例导引与其各种改进方法因其结构简单、易于实现及有效性得到了广泛应用［1-2］。文献［3］运用比例导引律（Proportional Navigation，PN）研究理想导弹在不同初始条件下对目标的拦截问题，文献［4］基于纯比例导引律（Pure Proportional Navigation，PPN）研究针对有界分段连续时变机动目标的捕获能力，在PPN 的基础上文献［5］考虑拦截碰撞角约束提出一种基于纯比例导引律的拦截碰撞角约束（Pure Proportional Navigation Intercept Angle Constraint Guidance，PPNIACG）制导算法。文献［6］研究扩展真比例导引律（Ture Pro‐portional Navigation，TPN），并将其应用于具有较小航向误差的简单拦截场景。文献［7］在比例导引律的基础上提出一种改进比例导引律，提高了针对大气层外高机动目标的命中精度。由上述研究可知，虽然比例导引及其变结构形式在制导律设计中得到了广泛应用，但其缺陷也在应用过程中逐渐凸显，当拦截机动能力较大的目标时，其拦截效果并不理想，甚至造成脱靶。

针对传统制导律存在的缺陷，随着经典控制理论的发展，将经典控制理论与制导方法相结合的现代制导理论逐渐得到发展。文献［8］考虑导弹三维制导问题中的耦合作用，提出了一种将有限时间控制和非线性干扰观测器相结合的复合制导控制方法，文献［9］运用神经网络对目标加速度进行预测，提出一种最优滑模制导律，并设计自适应开关项来处理执行器饱和误差及预测误差。文献［10］基于弹目相对视线方向与视线法向设计终端滑模双层协同制导律，并针对提出的制导律设计新的自适应律，用以加快滑模面的收敛速度。文献［11］以具有理想动态时滞的自动驾驶仪为前提，提出了滑模制导律，并将其推广到自动驾驶仪具有动态延迟的情况。文献［12］考虑攻击角约束、自动驾驶仪动态特性，设计一种固定时间收敛的新型非奇异终端滑模制导律，并设计固定时间收敛的滑模干扰器用于估计目标机动等干扰。文献［13］提出了一种基于最小控制力和末端位置、速度约束的最优策略，并将其与滑模控制相结合，得到鲁棒最优制导律，最后将此种方法推广至拦截任意时变机动目标。文献［14］提出一种针对机动目标，带有终端虚拟视线角约束、终端视线角约束的最优制导律，旨在以一定的末端攻击角度拦截目标。文献［15］提出了一种具有权重函数的最优制导律，使得导弹在全程制导过程中不需对制导律进行重新设计。文献［16］基于模型静态规划算法提出了一种考虑初制导与中制导的联合规划制导算法，用于解决多阶段、最优拦截制导问题。除此之外，一些新型制导方法也被广泛应用，文献［17］提出一种基于新型几何方法的拦截制导律，文献［18］基于经典微分几何曲线理论与Lyapunov 理论，提出一种新型的鲁棒几何方法制导律。文献［19］中针对高速机动目标，提出一种基于混合策略博弈理论的新型自适应加权微分博弈制导律，其权重依据目标加速度的估计误差进行设计。文献［20］针对非线性动态控制系统在给定时刻的闭环制导问题，提出了一种模糊组合制导律，文献［21］中基于PN 方法提出了一种模糊控制方法，通过模糊逻辑控制器改变等效导航常数值，以达到导弹最好性能。文献［22］基于监督学习，运用具有比例导引律的导弹系统生成大量数据训练深度神经网络得到制导策略。尽管目前诸多算法在拦截非机动目标与机动目标时均具有明显效果，但算法中仍有诸多角度、时间等约束，并且需明确目标运动信息。

在经典制导律与现代制导律存在缺陷的基础上，随着人工智能的快速发展，机器学习被广泛应用于解决决策问题。强化学习（Reinforce‐ment Learning，RL）作为机器学习中的一个重要分支，被引入到制导律设计中，此算法能够将观察到的状态直接映射到动作。在与环境进行交互的过程中，通过不断学习、试错的方式采取动作信息来影响系统的状态，从而最大化所获得的奖励，即随着时间的推移能够不断进行学习寻找最优策略的过程［23］。将强化学习方法与制导、导航与控制领域相结合，能够克服基于模型的传统方法需要系统模型和完整地环境信息的局限性问题［23-24］。在强化学习中通常选用策略函数、价值函数等不同的优化目标以及不同的函数逼近器来近似策略、价值函数或者他们的组合［25］。

文献［26］基于Q 学习方法设计零控脱靶制导律，并在垂直平面上验证算法的有效性。文献［27］设计了一种基于微分对策方法的神经网络制导律，面向二维平面内的追逃问题进行研究。传统的强化学习算法往往采用离散的状态与动作空间，所以“状态-值”函数可以用状态的查找表表示。但在实际复杂任务中往往需要较大的状态空间及连续的动作空间［28］。为避免状态、动作空间过大而造成的维数“灾难”问题，通常使用由神经网络构成的函数逼近器或“动作-评价”智能体结构搭配实现具有连续状态、动作的强化学习算法［24］。文献［29］中将卷积神经网络引入到强化学习算法中，提出了深度Q 学习算法，并提出了深度强化学习（Deep Reinforcement Learn‐ing，DRL）相关概念。深度强化学习算法结合了强化学习中的决策能力与深度学习（Deep Learn‐ing，DL）的特征提取能力。文献［30］应用动作-评价（Actor-Critic，AC）深度强化学习算法研究其在导弹突防问题中的实用性。文献［31］考虑数据运用效率，基于模型预测路径积分控制方法设计基于模型的深度强化学习制导律，文献［32］将元学习与近端策略优化（Proximal Policy Opti‐mization，PPO）算法相结合对制导律进行设计，且所设计的制导律不需目标与拦截器的距离估计。文献［33］基于深度确定性策略梯度（Deep Deterministic Policy Gradient，DDPG）算法设计多智能体深度确定性策略梯度（Multi-Agent Deep Deterministic Policy Gradient，MADDPG）算法解决不同情况下多智能体的防御和攻击问题，文献［34］运用DDPG 算法学习行动策略，将所观察到的状态映射到制导指令中。文献［35］中针对弹道导弹终端拦截问题，设计基于双延迟深度确定性策略梯度（Twin Delayed Deep De‐terministic Policy Gradient，TD3）算法的制导策略。在上述研究中，强化学习算法的学习、训练效率仍然是目前研究的难点问题，本文结合神经网络函数逼近器与“动作-评价”智能体结构的优势，运用深度强化学习中的信赖域策略优化（Trust Region Policy Optimization，TRPO）算法对拦截制导问题进行研究，对训练数据进行充分运用，提高训练效率。

本文研究深度强化学习算法在导弹拦截制导问题中的应用，首先建立拦截弹与目标间的相对运动模型，将其作为深度强化学习智能体的训练环境。其次设计基于TRPO 算法的制导算法，其输入为状态，并将状态直接映射为动作即加速度制导指令，通过对交战训练场景、状态空间、动作空间和奖励函数进行设计，以完成对制导算法的训练。其中奖励函数的设计对强化学习算法的训练尤为关键，好的奖励函数能够加速训练过程的收敛，坏的奖励函数会导致收敛时间加长甚至无法收敛。因此，奖励函数设计结合状态空间中相对距离、相对视线角、相对视线角速度以及能量消耗等因素，能够充分反映拦截弹与目标的系统状态。最终设置不同初始条件完成对环境的训练，主要包含2 种：①特定初始条件下对智能体进行训练；②随机初始条件下对智能体进行训练。

训练完成后，通过仿真验证所设计制导算法的有效性，主要对不同初始状态的学习场景和未学习场景进行测试，测试结果显示所设计的制导算法具有一定鲁棒性、泛化能力。

1 深度强化学习及TRPO 算法

深度强化学习（Deep Reinforcement Learn‐ing，DRL）将强化学习与深度学习进行结合，运用深度神经网络作为函数逼近器。TRPO 算法位于同策略（On-policy）与异策略（Off-policy）强化学习方法的交界处。虽在算法设计过程中使用新、旧2 种策略网络，并运用旧策略（Oldpolicy）进行重要性采样，但真正的异策略算法可以用任意策略网络生成的数据更新目标策略网络，而TRPO 算法新、旧策略比例受到一定约束，并且旧策略权重由新策略软更新得来，此方法保证新策略应用旧策略采样所得到的数据更新参数时更加有效。

在强化学习中，智能体与环境进行不断的交互，在交互过程中试图通过不断试错的方式调整、优化策略来解决系统所存在的问题。在学习过程中，智能体（Agent）产生动作at∈A，传送到环境（Environment）对状态st+1∈S及奖励rt+1(st，at)∈R进行更新，并收集返回到智能体进行经验收集、分析后优化策略π(a|s)，通过最大化收集到的奖励rt+1(st，at)∈R找到一个最优策略π∗(a|s)［36］。其中涉及到马尔可夫决策过程、策略梯度、优势函数等方法。

1.1 马尔可夫决策过程

马尔可夫决策过程（Markov Decision Pro‐cess，MDP）本质为一个随机过程，表示序列决策建模的理论框架，通过此框架强化学习中环境与智能体的交互过程以概率论的形式表现出来。马尔可夫决策过程被定义为M=。

在MDP 中，智能体在时间序列t时观察到环境状态st∈S，并依据状态st采取一个动作at∈A积分得到t+1 时刻状态st+1∈S。同时，为评估状态转换的好坏程度，智能体得到即时奖励rt+1(st，at)∈R，γ表示未来奖励的折扣因子，P表示状态转移概率。交互过程如图1 所示。

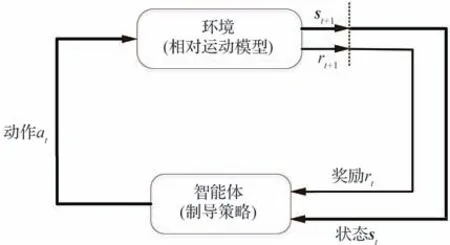
图1 “智能体-环境”交互Fig.1 “Agent-environment” interaction

图1 中“环境”代指所建立的拦截弹-目标相对运动模型，“智能体”代指基于信赖域策略优化算法的制导策略。

MDP 与智能体共同给出了一组序列：

式（1）所示的序列中主要包括2 种状态转换：一是状态到动作的转换由智能体的策略π(a|s)决定；另一种是由环境决定的动作到状态的转换。

智能体在状态st时的动作选择被建模为策略π(at|st)的映射，将环境的状态值st映射到一个动作集合的概率分布或者概率密度函数：

在强化学习中，累积奖励被定义为与时间序列相关的表达式：

“状态-值”函数定义为当我们采取了某一策略π(a|s)后，累计回报在状态st时的期望值：

在马尔可夫决策过程中，拥有各种各样的策略π(a|s)，策略优化过程为得到一个最优策略π∗(a|s)，需获得最大化的折扣奖励：

式中：γ∈(0，1]为奖励函数折扣因子，对未来奖励进行考虑加权，当γ→0 时，更加注重目前的奖励；当γ→1 时，会更优先考虑未来的奖励。

1.2 策略梯度

策略梯度算法的基本思想是通过学习策略π(a|s)对性能函数J(π)=Vπ(s)进行最大化。针对复杂的目标与拦截弹的交战环境，其连续动作空间及状态空间较为庞大，为更好地近似策略函数π(a|s)，其策略网络由带有权重θ的深度神经网络构成，其策略函数参数化可以近似表示为πθ(a|s)。神经网络与强化学习结合为深度强化学习算法。神经网络是依据一系列层组成的输入输出系统，每一层均包含有限个神经元。策略网络内部结构如图2 所示，评价网络内部结构与策略网络内部结构相似。

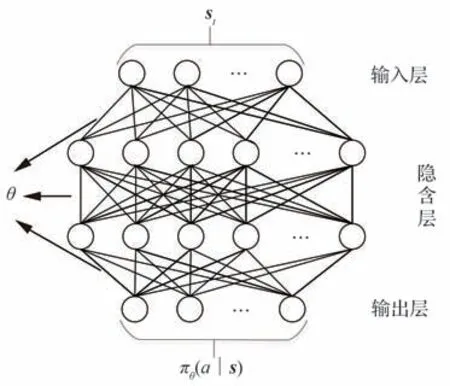
图2 策略（动作）神经网络内部结构Fig.2 Policy（action）neural network interior structure

在神经网络中对权重参数进行更新以最大化性能目标函数J(πθ)：

策略梯度算法主要依据随机梯度上升法对权重参数θ进行更新：

式中：α表示策略网络的学习率，决定了梯度更新的步长。

由策略梯度定理得知，估计策略函数的梯度表示为

式中：b(st)表示基准函数。

将式（8）改写为策略梯度的损失函数［37］：

利用式（9）损失函数进行参数优化将会导致参数空间中出现多种相似的轨迹，且所提出的∇θ J(θ)前面的每一次更新都会对后续更新产生影响，并最终影响训练效果。为解决上述缺陷，采用信赖域策略优化（TRPO）算法设计制导策略。

1.3 优势函数

本节中，基于“状态-值”函数式（4）引入“状态-动作-值”函数，并通过两者定义优势函数。

“状态-动作-值”函数表示当状态st与动作at均确定时长期期望奖励：

“状态-值”函数与“状态-动作-值”函数均表示为长期期望奖励，当对所有动作的“状态-动作-值”函数求期望便可以得到“状态-值”函数表达式，具体表示为［23］

基于“状态-值”函数式（4）与“状态-动作-值”函数式（10），可得到优势函数表达式：

1.4 信赖域策略优化算法

在信赖域策略优化（TRPO）算法中，通过设置Kullback-Leibler（KL）散度值来约束新、旧策略比例，使梯度步骤更新后的新策略与旧策略间差别减小，但同时TRPO 方法又采取了较大的更新步长来更新策略参数，目的为提高算法的性能。其中散度为新旧策略概率分布间的量度。

在信赖域策略优化函数中，为最大化目标状态的期望回报，引入一个新的函数定义η(π)，将期望折扣奖励式（4）进一步表示为

基于式（12）与式（13），策略πθ的预期回报为

针对式（16）等号右端第2 项，所有动作的选择均是由旧策略进行采样，因此当状态st时，运用文献［39］所介绍的重要性采样及式（15）对其进行改进：

为保证式（20）更好地逼近、替代预期回报式（14），应限制策略更新幅度，因此为避免局限性，信赖域策略优化算法引入KL 散度衡量新策略与旧策略概率分布间差异，其被定义为所有状态中最大动作分布的总变差散度DTV，表示为

若直接对上述目标函数进行优化，由式（23）可得，惩罚系数ε较大，导致KL 散度较小，最终导致在策略优化过程中，对策略更新幅度较小，即式（23）中惩罚系数ε在一定程度上限制步长，为增大步长将惩罚系数变为约束项：

式中：δ定义为约束因子。

在策略优化的过程中，需对式（24）所示的目标函数最大化以得到下一步参数θ。为进一步优化目标函数，将约束项KL 散度用其期望代替，且权重为旧策略稳定状态分布表示为

最终目标函数为

目标函数优化过程中，依据式（13）和式（20）可得知旧策略下的期望折扣奖励与新策略参数πθ是相互独立的，因此依据式（23）针对目标函数的优化可进一步简化为

本文中信赖域策略优化算法是依据“动作-评价”网络架构进行设计的，在训练过程中评价网络针对策略网络产生的策略进行评估，并运用TD-error 设计评价网络目标函数：

因此依据策略网络目标函数式（27）与评价网络目标函数式（28）运用优化器与梯度上升方法对网络参数进行更新：

式中：k和k+1 分别表示当前训练集与下一训练集；α和β分别为策略网络与评价网络的学习率；并设计Ke限制每次更新频率，提高训练效率。旧策略网络的参数则由新策略网络参数软更新得到。

2 基于深度强化学习的制导问题描述

本文主要考虑拦截弹与目标相对运动模型，暂时不考虑拦截弹、目标绕质心转动的姿态运动，并将其应用于深度强化学习制导策略设计中。首先提出以下3 个假设［35，41］：

假设1将地球视为均值的球体，对末制导进行设计，因时间较短，忽略掉地球自身的旋转角速度。

假设2将拦截弹视为理想刚体状态，不考虑拦截弹所存在的可能性弹性形变，并将拦截弹与目标视为常值速度的质点运动。

假设3将拦截弹系统状态视为理想制导状态，暂不考虑执行结构的动态特性。

2.1 交战环境

使用一个简洁的拦截弹与目标相对运动场景，并且主要针对拦截弹与目标二维垂直平面内的制导问题进行研究，但研究结论可以推广到三维空间。两者纵向平面内相对运动场景如图3所示。

图3 拦截弹-目标相对运动环境Fig.3 Interceptor-target relative motion environment

图中：M和T分别表示拦截弹与目标质点。在双方交战过程中，当目标飞行器T进入到探测范围后，发射拦截弹M运用所设计的制导策略拦截目标T，同时目标T采取相应的策略进行规避，直至拦截成功或失败。坐标系OXY为惯性坐标系；q表示弹目相对视线角；瞬时相对距离表示为R；Vm和Vt分别为拦截弹与目标的运动速度；φm和φt为拦截弹与目标之间的弹道倾角；am和at分别表示拦截弹与目标垂直于速度方向的法向加速度。

根据图3 交战场景，我们给出拦截弹与目标在二维平面内运动学模型：

描述拦截弹与目标相对运动的方程为

拦截弹与目标垂直于速度方向的加速度与速度间的关系可表示为

直接应用拦截弹与目标相对运动方程作为深度强化学习环境，以便于更加直观的计算、观测系统各状态变量。

2.2 制导算法设计

在本节中，提出一种基于信赖域策略优化（TRPO）算法的制导算法设计方法，在智能体训练过程中将状态直接映射到拦截弹的制导指令，并通过不断地学习得到最优策略。本文所设计制导算法具体结构如图4 所示，详细描述制导算法的内部结构。为顺利训练TRPO 制导算法，对制导算法中作战训练场景、状态空间、动作空间、奖励函数及网络结构五方面进行详细设计。

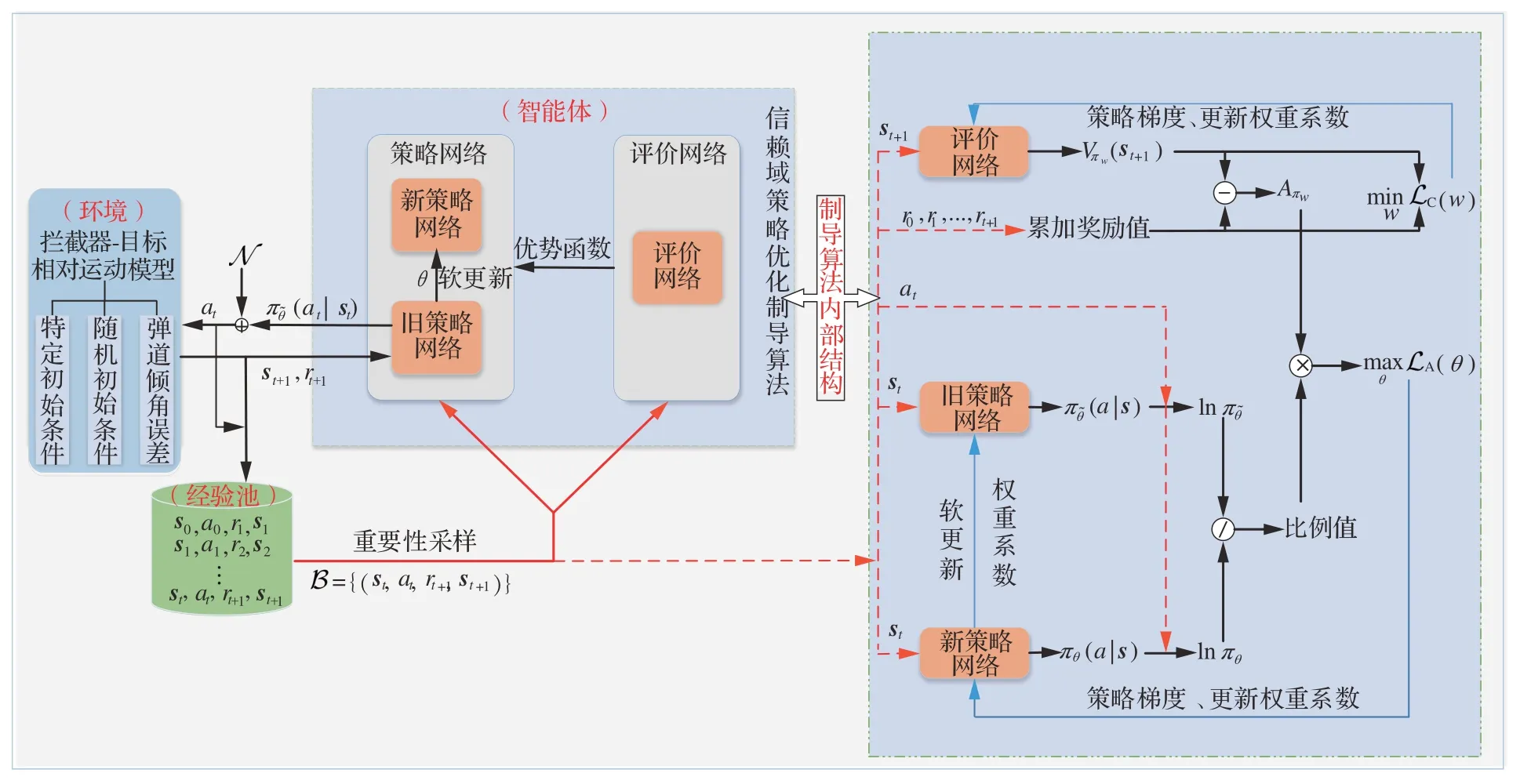
图4 信赖域策略优化制导算法全结构Fig.4 Trust region policy optimization guidance algorithm full structure

2.2.1 训练场景

本文所研究的深度强化学习制导算法训练场景是基于所建立的拦截弹与目标在二维垂直平面内的相对运动模型构建的，其在训练过程中与智能体直接进行交互，为更好地对模型进行训练，获得最优策略。为降低训练算法的随机性，设定随机初始条件范围，其初始条件设置包括拦截弹与目标的初始位置、速度等，相应初始相对视线角及初始弹道倾角由初始条件推导可得，训练交战环境如图5 所示。图5 中φmmax、φmmin、φtmax和φtmin分别表示拦截弹与目标弹道倾角最大值与最小值；qmax和qmin分别表示相对视线角的最大值与最小值；ximax、ximin、yimax和yimin(i=m，t)分别表示拦截弹和目标的初始位置边界。设置环境各参数在训练过程中的约束条件如表1所示。

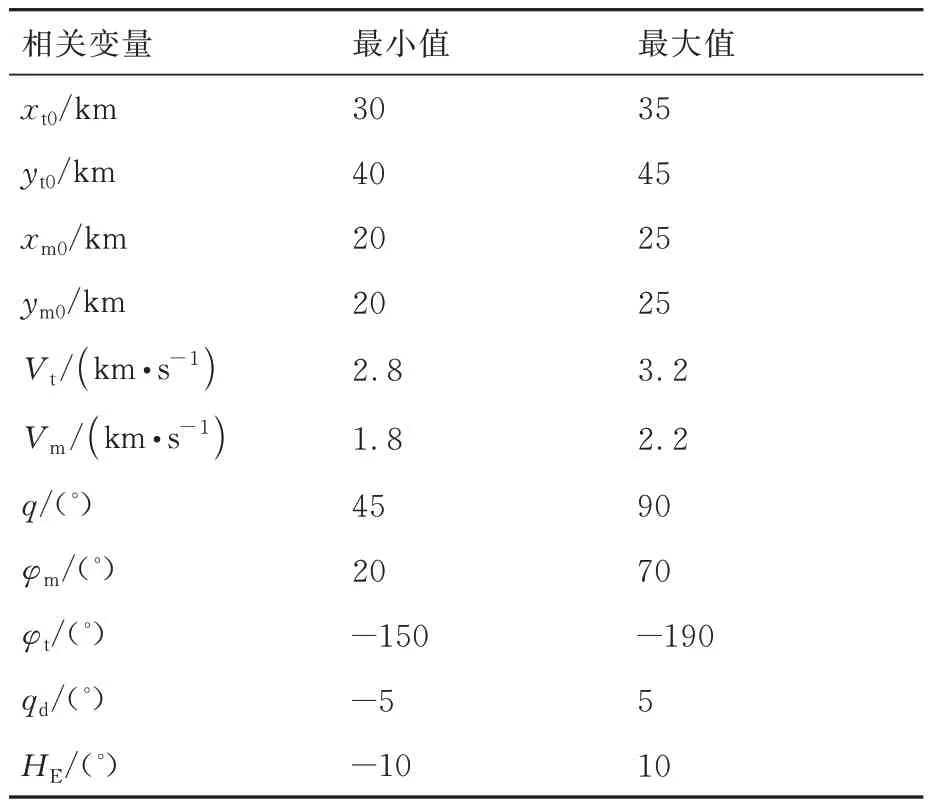
表1 训练场景参数边界Table 1 Training scenario parameters constraints

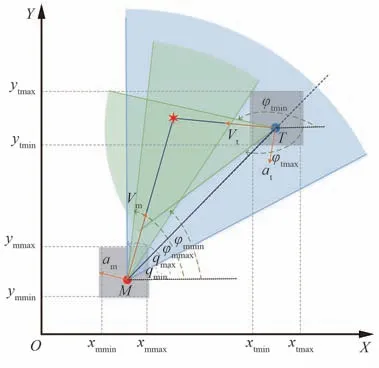
图5 训练交战场景Fig.5 Training engagement scenario

在拦截弹与目标位置、速度通过随机初始化确定后，两者初始相对距离与初始相对视线角可表示为

式中：(xm0，ym0)与(xt0，yt0)分别表示为拦截弹与目标的初始位置；qd表示初始视线角误差，初始化时对其在设定范围内进行随机初始化。

在相对视线角基础上，目标初始弹道倾角可表示为

式中：HE表示拦截弹与目标的初始弹道倾角误差，当HE=0 时表示目标速度指向拦截弹方向，但训练过程中每一训练集开始时均在表1 所设定的范围内对HE进行随机初始化，即HE并不为0，目标速度并不直接指向拦截弹，更加符合实际任务需求。

拦截弹初始弹道倾角表示为

式中：q0表示为拦截弹与目标间的初始相对视线角，由式（34）确定；等号右端第2 项考虑目标速度垂直于初始视线角的分量对拦截弹初始弹道倾角的影响；等号右端第3 项与目标初始弹道倾角计算同理，当HE=0 时拦截弹速度指向目标，但同样在每一训练集中进行随机初始化，使HE≠0。

当式（35）与式（36）中初始弹道倾角误差HE均为0 时，目标与拦截弹满足不机动情况下的碰撞三角形如图5 所示。但实际训练过程中，在每一训练集开始对两式中的初始弹道倾角误差HE分别进行随机初始化，且两者取值并不一致，使目标与拦截弹速度均不指向对方，更加贴合实际需求。

训练过程中，目标飞行器采用方波机动：

式中：nt表示目标最大机动过载；g表示重力加速度；ωf表示方波机动频率；Δt表示为机动持续时间；Rtm表示目标开始机动时拦截弹与目标的临界距离；ΔT为机动所持续的最大时间。

2.2.2 状态空间

为了更好地训练所设计的TRPO 制导算法，在构造状态空间时，既要考虑到拦截弹与目标交战系统变量的多样性，又要考虑智能体能够更好提取状态变量的关键信息，运用神经网络进行非线性拟合。因此状态变量的选择应尽可能反应系统重要信息，并尽可能简洁，以减小智能体所需要搜索的状态空间，加快智能体的训练速度。基于式（32）所示的拦截弹与目标二维交战运动方程，将环境状态空间设为

选定拦截弹与目标相对距离、相对视线角、相对距离变化率和相对视线角速度4 个元素作为环境状态量，其能够充分反应拦截弹与目标相对位置信息，且相对视线角应尽可能变化小，以尽可能的满足平行接近。

2.2.3 动作空间

深度强化学习中，根据特定任务需要，动作空间需设计为离散动作空间或连续动作空间。设计的TRPO 制导算法作为生成制导指令的策略，依据拦截任务需要采用连续动作空间进行描述。制导指令由相关状态变量进行直接映射：

式中：ft(⋅)表示非线性函数，由神经网络拟合而成。

制导指令设置在最大过载范围内：

式中：nm表示为拦截弹最大的法向过载。

2.2.4 奖励函数

奖励函数作为TRPO 制导算法中最重要的一部分，合适的奖励函数能够更好地辅助训练智能体。在拦截弹与目标相对运动过程中，系统需要针对每一步返回一个即时奖励到智能体，更直观地反映系统状态好坏。设计的制导算法需要使拦截弹能够不断地接近目标最终成功拦截。奖励函数的具体形式为

式中：rp表示为拦截弹与目标相互接近过程中奖励函数，即为过程奖励函数；re表示拦截弹是否成功拦截目标的终端奖励，若成功拦截则给出一个正奖励。

rp和re的具体形式可表示为

式中：过程奖励函数等号右端第1 项为拦截弹与目标相对距离的直观奖励，当拦截弹不断接近目标时则给出正奖励，距离越近奖励值越高，kr表示相对距离权重系数；等号右端第2 项对拦截弹能量消耗进行考虑，使拦截弹在拦截目标的同时尽量保证较少的能量消耗，ka表示能耗权重系数；等号右端第3 项与第4 项均与相对视线角有关，使拦截弹在不断接近目标的同时保证相对视线角的变化量与变化率尽可能小，以保证拦截弹尽可能以平行接近的方式拦截目标，ks1和ks2表示相对视线角及视线角变化率权重系数；re表示终端拦截成功时直接加入一个正值奖励a1，用于区别普通过程奖励，使本文所设计的制导算法在训练过程中朝此方向优化；Rm表示拦截成功时最小脱靶量。

2.2.5 网络结构

信赖域策略优化（TRPO）算法属于强化学习中“动作-评价”算法，其中包括策略（动作）与评价2 种网络结构。2 种网络均由4 层全连接神经网络构成，其中包含一个输入层，2 个隐含层与一个输出层，其网络结构均如图2 所示。4 层全连接神经网络中每层具体单元数、激活函数如表2 所示。

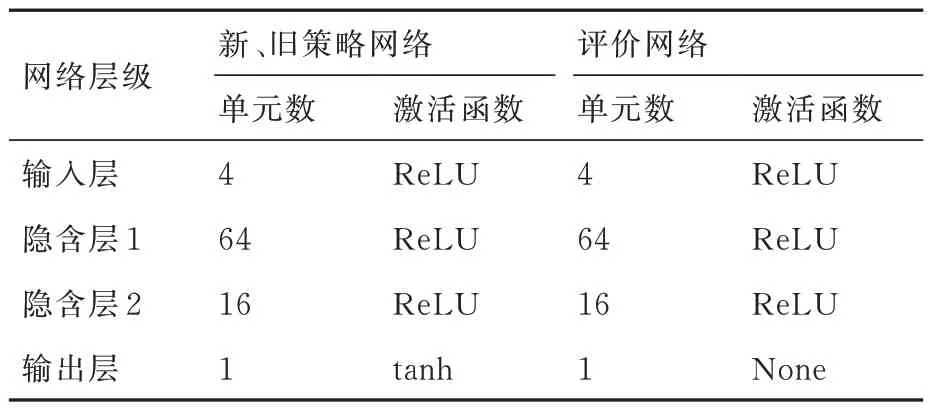
表2 策略与评价网络结构Table 2 Policy and critic network structure

策略网络与评价网络中输入层、隐含层的激活函数均为ReLU 函数，此种激活函数比其他非线性激活函数具有更快的处理速度，并在一定程度上缓解梯度消失的问题，其具体表达形式为

动作网络为将动作范围限制在［−1，1］内，其输出层激活函数为tanh 函数，既能够防止制导机构饱和，又便于对制导指令按照最大过载nm进行精确缩放，其具体表达式为

式中：z表示激活函数的输入变量。

2.2.6 训练流程

针对2.2.1～2.2.5 节所建立的拦截弹与目标相对运动交战环境与基于信赖域策略优化算法的制导算法进行交互训练。在介绍具体流程前首先进行变量初始化：一是相关超参数初始化包括折扣系数γ，约束因子δ，更新频率Ke，经验池大小|D|，最小批量大小|B|，训练集数nepisodes，每集训练最大步长nsteps，策略网络学习率α及评价网络学习率β；二是交战环境参数边界初始化包括拦截弹与目标初始位置(xm0，ym0)、(xt0，yt0)，初始速度Vt、Vm，初始弹道倾角误差HE，初始视线角误差qd，初始弹道倾角φt0、φm0，初始视线角q0等。后续具体训练流程如算法1 所示。

3 仿真校验

3.1 训练超参数

深度强化学习中各超参数的取值对训练效果有明显的影响，实际训练过程中针对不同环境、不同任务需求，其调参过程、最终参数取值并不唯一。针对2.2 节给出的拦截弹与目标的正面接触场景及所设计的状态空间、动作空间、网络结构及奖励函数等，通过多次调参试错，给出训练中最佳效果的超参数值，如表3 所示。

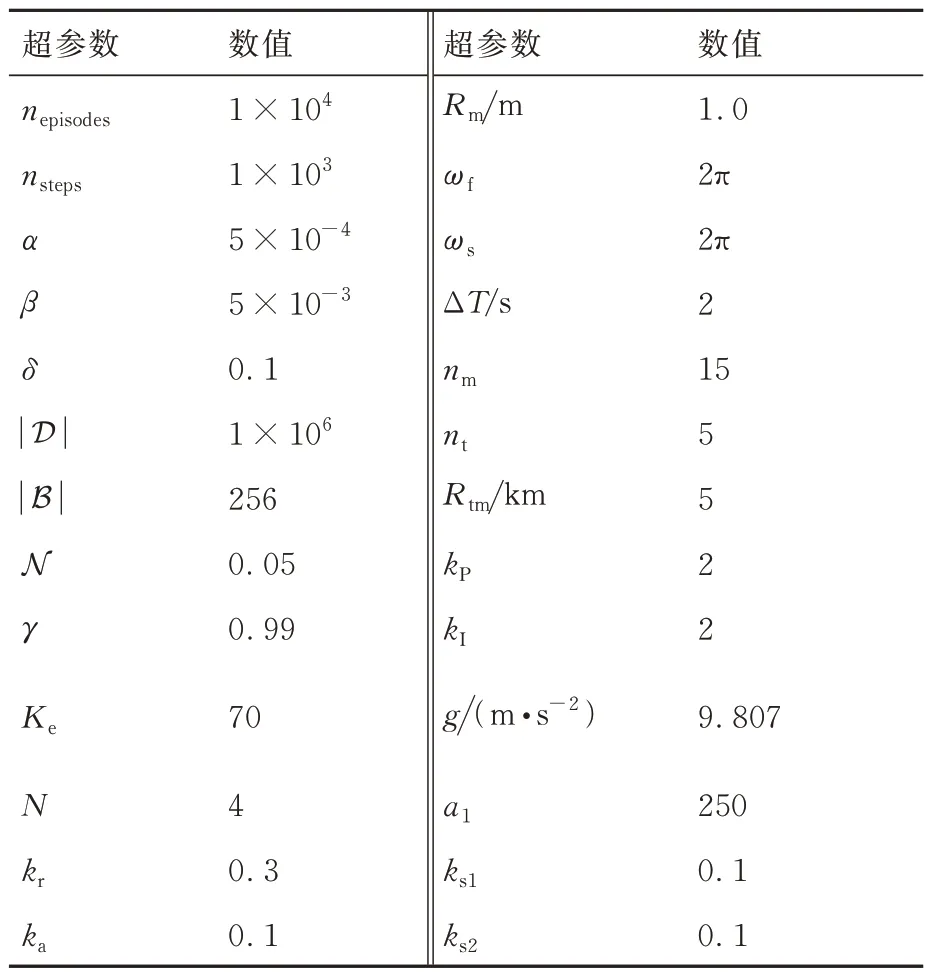
表3 训练超参数设计Table 3 Training hyper-parameters design

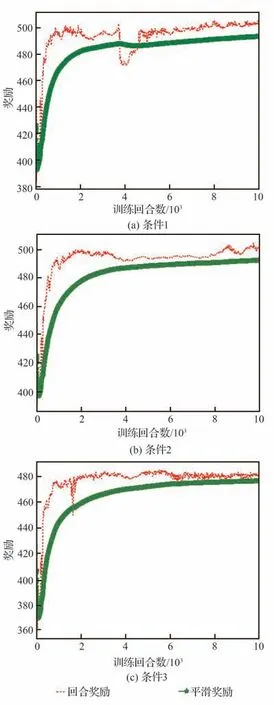
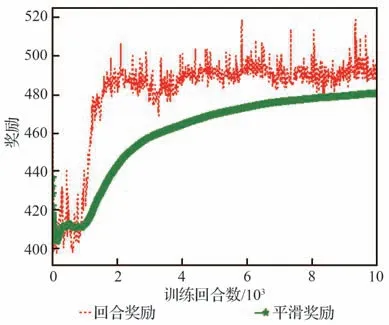
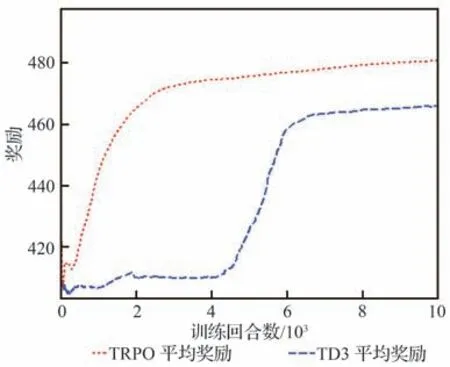
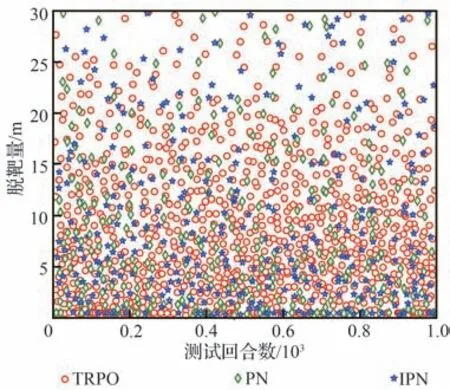
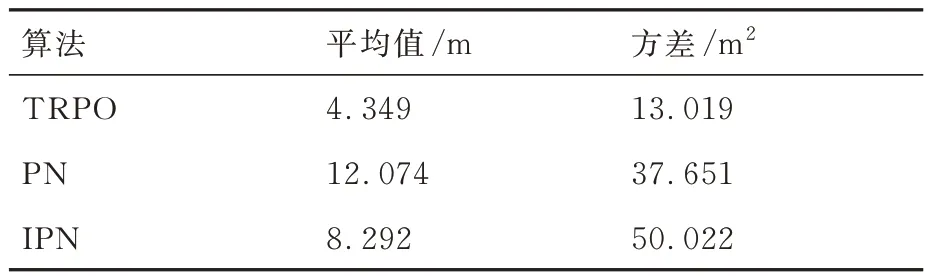
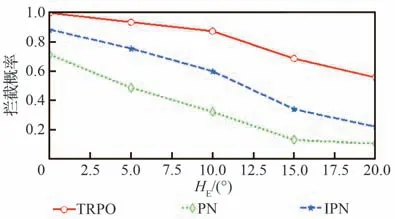
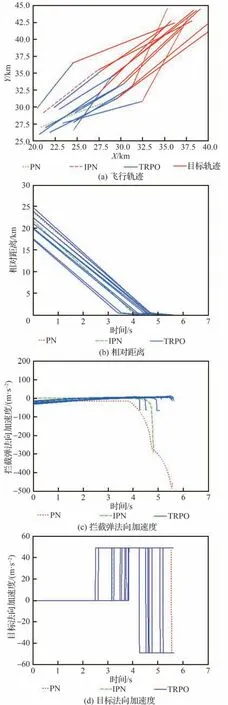
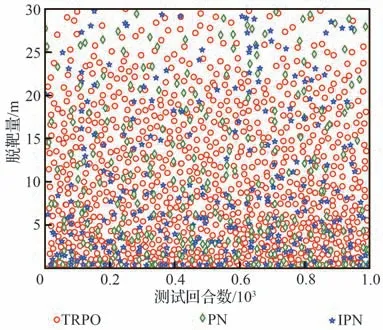
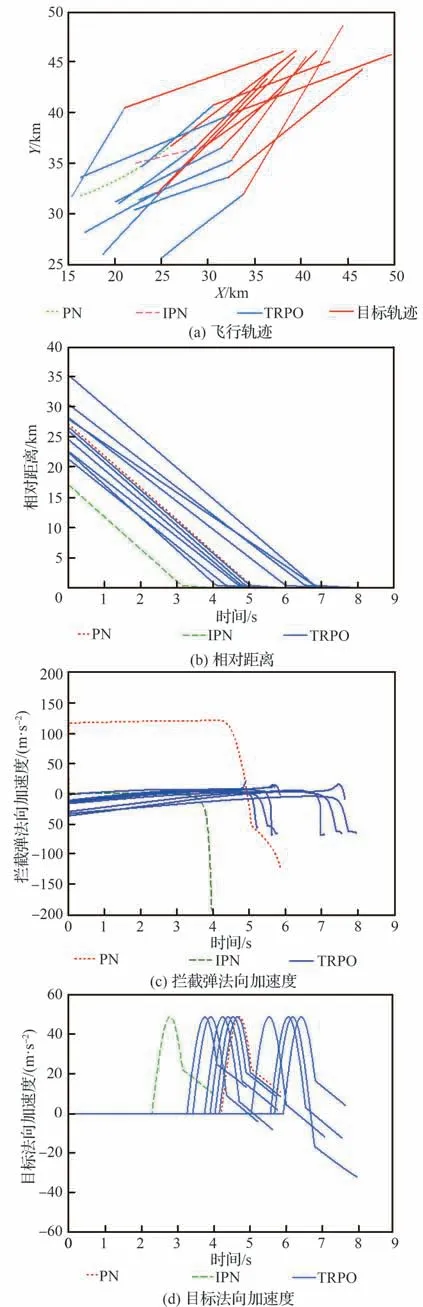
表3 中训练集数nepisodes与每集最大训练步长nsteps取值依据弹目相对距离、两者速度大小，保证每集最大训练步长内能够成功拦截，且多次训练中保证算法能够在训练集数内收敛。策略网络与评价网络学习率α和β依据训练经验评价网络学习率设计比策略网络高一数量级。依据拦截任务中数据量经验池大小|D|一般选为1×106～5×106，最小批量数据|B|通常选为128∼512，约束因子δ一般设为0.1～0.3，更新频率Ke取值限制网络参数更新频率，通常选为60 ∼90，奖励折扣系数γ通常选为0.99～0.999，合适的参数能够在训练过程中使训练更加高效的同时，尽量减小计算量。过程奖励函数中弹目相对距离系数kr，能耗系数ka，相对视线角及视线角速度系数ks1和ks2为使奖励不会过大导致计算量增加，又能够在弹目相对运动中给出明显的正负奖励，取值范围选定为0.1～1，且在本文算法设计中更加注重相对距离因素，故弹目相对距离权重系数取值相对较大。脱靶量Rm表示弹目距离

3.2 训练过程

训练、测试仿真验证均依托于Python 3.8 和PyTorch 1.10.2 框架，计算机硬件信息为 i5-10400F CPU @ 2.90GHz，32G DDR3，1T SSD，NVIDIA GeForce GTX 1650。

在训练过程中，最大训练集被设定为1×104，每一集中最大训练步长为1 000。在每一训练集开始首先对拦截弹-目标相对运动环境进行特定或随机初始化，得到初始化观测状态s0，而后智能体依据此状态得到相对应的动作a0，环境得到动作指示后，依据动作运用四阶龙格库塔积分得到下一步状态st+1，起始积分步长选定为0.01，当相对距离R<500 m 时积分步长选为0.001，并获得奖励值rt+1，而后将状态输入到智能体，循环此过程，直到拦截目标或步长达到最大值后进入下一训练集。最终直到获得最佳的制导策略。同时将一系列状态、动作、奖励等值存入经验池，每5 次循环对智能体进行一次训练并运用优化器、梯度算法更新网络参数，每次更新中依据参数δ与Ke对网络参数更新幅度及频率进行控制，且在动作选择时加入随机噪声N 用以估计执行结构等引起的误差。

训练过程中，为保证所设计制导算法具有应对多种初始情况的能力，主要针对2 种场景进行训练：一种为特定初始条件下拦截弹-目标相对运动环境，对拦截弹与目标初始位置、初始速度进行设定，并列举3 种具有代表性初始特征点如表4 所示，相应的学习曲线如图6 所示；另一种是随机初始条件下拦截弹-目标相对运动环境，使拦截弹与目标初始位置、初始速度每集训练时在表1 设定范围内进行随机选择，其学习曲线如图7 所示。

表4 训练初始条件Table 4 Training initial condition

图6 特定初始条件下学习过程Fig.6 Learning process with fixed initial conditions

图7 随机初始条件下学习过程Fig.7 Learning process with random initial conditions

学习曲线图6（a）可看出条件1 时，在1 000 训练集内奖励得到有效提升，并在4 000 集左右有明显波动，5 000 集后训练曲线能够基本保持稳定，奖励值最终在500 左右波动。图6（b）可看出条件2 学习曲线在1 000 集内得到提升，且最终能够基本稳定在490～500 之间。由图6（c）可以看出条件3 学习曲线在训练集2 000 以内提升、波动，最终奖励值在5 000 集后能够稳定在480 左右。由3 组特定条件下学习曲线可得出，虽然因为初始条件的差异，奖励曲线最终稳定值不同，但均有较好的学习效果，证明所设计的制导策略针对不同初始条件，具有一定的鲁棒性。

根据图7 随机初始条件下的学习曲线可看出，奖励在2 000 集以内得到快速的提升，且在2 000 集后维持在480～500 间波动，由学习曲线可得知在随机初始条件下虽比特定初始条件下波动明显，但仍然能够得到理想的训练效果，且随机初始条件的训练更加符合现实任务需要。经上述训练曲线分析表明所设计的TRPO 制导算法针对不同特定初始条件、随机初始条件的训练场景均具有一定的稳定性，能够及时收敛。

为进一步对TRPO 制导算法训练效率提升效果进行验证，运用本文所设计的TRPO 制导算法与文献［35］提出的双延迟深度确定性策略梯度（TD3）制导算法对随机条件下拦截弹与目标相对运动环境进行训练，图8 显示训练过程中平均奖励对比曲线。由图8 中可得知TRPO 制导算法在2 000 集以内得到收敛，而TD3 方法在4 000～6 000 集间进行收敛。表明本文提出的TRPO 制导算法比TD3 制导算法收敛更快速，且最终平稳奖励值更高，由此验证TRPO 制导算法对训练数据利用率更高，提高了训练效率。

图8 奖励函数对比曲线Fig.8 Reward function comparison curves

3.3 测试过程

为验证3.2 节训练的TRPO 制导算法的有效性、鲁棒性及在不同初始条件下拦截不同机动模式目标的泛化性，对所设计的TRPO 制导算法进行2 种场景下的测试验证：一是在学习场景下进行测试；二是在未知场景下进行测试。测试过程中考虑拦截弹在临近空间环境的复杂性，易受到风场等干扰，在测试中对弹道倾角φm加入5%实时误差，验证本文所设计的深度强化学习算法在拦截目标时具有应对干扰的能力。并将测试结果与传统的比例导引律（PN）及改进比例导引律（IPN）结果相比较，验证算法的高效性。

PN 和IPN 具体形式为［42］

3.3.1 学习场景下测试

本节基于上文建立的拦截弹-目标交战环境，运用随机初始条件下训练的制导算法，并与随机初始条件下训练过程采用相同的参数，具体取值如表3 所示，同时目标进行方波机动如式（37）所示。在学习场景下采用蒙特卡洛打靶法进行1 000 次打靶仿真对所设计的制导算法进行测试，并将结果与PN、IPN 仿真结果相比较，验证算法的优越性，脱靶量散点分布如图9 所示。

图9 学习场景下脱靶量分布Fig.9 Miss distances distribution in learned scenarios

由图9 可得知在15 m 处脱靶量分布逐渐密集，且越靠近0 m 分布越密集。统计不同导引律脱靶量平均值及方差特性如表5 所示。由表5 中数据可得知与传统的PN、IPN 相比，所提出的深度强化学习制导算法脱靶量具有明显的减小，平均值基本能够维持在4.5 m 以内，由方差值大小可得出TRPO 制导算法相较于PN、IPN 脱靶量波动更小，拦截效果更加平稳，验证提出的深度强化学习制导算法具有一定的优越性。

表5 脱靶量统计Table 5 Statistics of miss distances

为进一步测试提出的深度强化学习制导算法在不同初始弹道倾角误差下的性能，针对不同初始弹道倾角误差分别进行1 000 次蒙特卡洛仿真实验，并分别记录不同弹道倾角误差下的拦截概率，其性能对比如图10 所示。由图10 可得知，TRPO 制导算法在不同弹道倾角误差下性能均优于传统PN、IPN 制导律，且随着初始弹道倾角误差的增大，优势更为明显，表明所设计的制导算法对中末交班条件要求更低，初始弹道倾角误差容错率更高，能够一定程度上对拦截弹中制导误差进行修正。另一方面在测试过程中所设计的弹道倾角基础上增加5%实时误差，用于模拟外部环境干扰，拦截结果表明所设计的深度强化学习制导算法具有应对外部干扰的能力。

图10 学习场景下拦截性能对比Fig.10 Comparison of interception probability in learned scenarios

拦截过程中，为更加直观的展现所设计的TRPO 制导算法针对不同位置、速度来袭目标的拦截效果，选取学习场景下10 组拦截弹与目标运动状态与1 组传统PN、IPN 拦截过程进行记录绘图，拦截测试中拦截弹与目标运动轨迹、相对运动距离、拦截弹法向加速度及目标法向加速度如图11 所示，由图11（a）可更加直观的得到不同初始条件下的拦截效果，运用本文提出的TRPO 算法能够对不同初始位置、速度的目标进行有效拦截。由图11（b）可得出拦截弹与目标相对距离呈线性减小，当目标与拦截弹相对距离减小到一定程度时，本文设定为500 m，为了更加精确对目标进行拦截，积分步长减小，相对距离缩减变缓。由图11（c）拦截弹法向加速度曲线可得出TRPO 制导算法与传统PN、IPN 算法相比，法向加速度后期变化更为平缓。在接近目标时，拦截弹法向加速度增加是由于目标进行机动导致，与图11（d）中目标法向加速度变化曲线相对应，且由图可得知目标进行方波机动。但两者法向加速度均在所设计的加速度范围内，满足拦截要求。而由图11（c）可得知传统PN、IPN 算法的法向加速度不在所设定的范围内，易造成执行机构的饱和。

图11 学习场景下测试结果Fig.11 Test results in learned scenarios

3.3.2 未知场景下测试

为验证所设计的深度强化学习制导算法针对未知环境的适应能力，本小节中运用随机初始条件下训练的模型对未知场景进行测试，且在拦截测试过程中采用与随机初始条件下训练过程相同的超参数，具体取值如表3 所示，仿真仍然采用1 000 次蒙特卡洛打靶实验。其初始条件改变主要包括目标的机动方式、目标与拦截弹初始位置、速度变化等。其初始位置与速度主要针对超出随机初始条件范围的部分进行测试，具体位置、速度范围如表6 所示，其他训练场景参数边界值如表1 所示。目标机动方式选为正弦机动，进一步验证制导算法的泛化性。

表6 未知场景参数边界Table 6 Unlearned scenario parameters constraints

正弦机动具体形式表示为

式中：ωs表示正弦机动频率。

在正弦机动模式下，测试过程中脱靶量分布与传统PN 和IPN 算法对比如图12 所示，由图可知TRPO 制导算法脱靶量在20 m 以内分布逐渐密集，表明TRPO 制导算法对不同位置、速度及机动模式的来袭目标均具有较好的拦截效果。

图12 未知场景下脱靶量分布Fig.12 Miss distances distribution in unlearned scenarios

不同初始弹道倾角误差下的性能对比如图13 所示，由图得知TRPO 制导算法相较于传统制导律在不同初始弹道倾角误差时均具有更高的拦截概率，但在初始弹道倾角误差较大时，其拦截效果提升有轻微减小，后续研究中可对未知场景初始弹道倾角误差较大的情况进行改进。

图13 未知场景下拦截概率对比Fig.13 Comparison of interception probability in unlearned scenarios

为进一步直观的展现本文所设计的TRPO制导算法针对目标速度、位置超过训练过程中所设定范围、且机动模式改变时的拦截效果，同时记录不同制导算法在拦截过程中制导参数的变化情况，在未知场景下选取10 组TRPO 制导算法与传统PN 和IPN 算法拦截过程进行对比。详细拦截过程、弹目相对距离变化曲线及拦截弹、目标法向加速度如图14 所示。由图14（a）可知，当拦截弹与目标位置、速度位于所设定范围以外时，TRPO 制导算法仍具有很好的拦截效果，更加说明TRPO 制导算法的泛化性，可应用于多种拦截场景。由图14（c）可得知传统PN、IPN 制导律与所设计的TRPO 制导算法相比，法向加速度变化剧烈，且不在所规定范围内，容易造成执行机构饱和，消耗更多的能量。由图14（d）目标法向加速度变化曲线可看出目标在拦截过程后半程进行正弦机动。

图14 未知场景下测试结果Fig.14 Test results in unlearned scenarios

依据上述学习场景和未知场景下的测试仿真分析可得知，运用所设计的TRPO 制导算法针对不同位置、速度及不同机动模式的目标均具有较好的拦截效果，证实TRPO 制导算法具有泛化性，并具有一定的鲁棒性及应对外部干扰的能力，且相较于2 种传统制导律性能优势明显。在拦截过程中，深度强化学习制导算法运用神经网络对4 种状态变量进行拟合得到指令加速度，其计算量较小，经过在不同配置计算机上进行训练测试，均具有较快的收敛速度，且单次拦截测试均保持在1 s 内，表明所设计的TRPO 制导算法可应用于多种配置计算机。

4 结论

提出了一种拦截临近空间高超声速飞行器的信赖域策略优化（TRPO）制导算法。建立了拦截弹与目标相对运动交战模型，并与制导算法共同构建马尔可夫决策框架，依据实际任务需求设计状态空间、动作空间和深度强化学习制导算法中的网络结构以及结合相对距离、相对视线角及能量消耗等因素的奖励函数，并在算法训练过程中针对状态空间、奖励运用归一化方法加快学习速度。最终在学习场景和未知场景下运用蒙特卡洛打靶法对制导算法进行仿真验证，仿真结果表明：本文所提出的深度强化学习制导算法相较于传统比例导引律（PN）及改进比例导引律（IPN）具有更好地拦截效果，更小的脱靶量，更稳定的性能，在多种场景下具有一定的鲁棒性、抗干扰性及泛化性，并可适应于多种不同配置计算机。