雷诺应力与涡黏性模型的分离流预测对比分析

赵雅甜，邵志远，阎超，向星皓

1.中南大学 交通运输工程学院，长沙 410083

2.北京航空航天大学 航空科学与工程学院，北京 100191

3.中国空气动力研究与发展中心，绵阳 621000

流动分离与翼型和机翼气动特性息息相关，飞行包线也时刻受到流动分离的影响。现代飞行器愈发苛刻和复杂的飞行条件使得设计过程中对分离流动的准确预测愈发关键。然而，对于较大逆压梯度下的分离流动，精确的CFD（Com‐putational Fluid Dynamics）模拟仍十分困难［1-2］。包含展向流动的三维边界层分离和高速下激波诱导边界层分离等典型复杂流动现象对预测模型的精度提出了更高要求［3-4］。

湍流模型作为RANS（Reynalds Averaged Navier-Stokes Equations）方法的核心之一，对流场计算结果影响显著。第2 次阻力预测会议（The Second DPW）的分析结果显示，湍流模型对CFD 计算结果的影响最大，占到约15%［5］。湍流场中各参数脉动几乎均与几何边界相关，因此，当前尚不存在某种湍流模型可适用于全部流场。被广泛使用的涡黏性模型由于Boussinesq假设的“先天缺陷”，导致对分离流动预测失准［6］。不同于涡黏性模型，雷诺应力模型从雷诺应力输运方程出发，对雷诺应力直接求解，考虑了雷诺应力的对流和扩散和流动历史效应［7］。因此该模型被认为是最自然、最符合逻辑的模型［8］。NASA（National Aeronautics and Space Admin‐istration）在CFD 2030 远景中也将雷诺应力模型作为主要发展的RANS 方法之一［9］。基于该类模型，Rumsey 等［10］通过对亚声速驼峰算例和ONERA M6 机翼算例进行计算后，发现雷诺应力模型存在再附点附近流线后弯，但预测精度优于涡黏性模型。对于小攻角来流下的三维机翼激波位置预测较为准确。王圣业等［11］利用基于雷诺应力模型的分离涡模拟方法对 24.6°迎角钝前缘三角翼进行数值仿真，发现模拟结果明显好于传统基于线性涡黏模型的分离涡模拟方法。舒博文等［12］发现雷诺应力模型可在翼身接合区角区流动和三维强激波诱导分离等问题中得到正确的流动特征。

然而，雷诺应力模型当前也存在诸多问题。熊莉芳等［13］研究发现，雷诺应力模型对边界条件十分敏感，对计算网格要求苛刻，数值稳定性较差。为解决数值刚性和边界条件奇性问题，Men‐ter 和Egorov［14］提出Stress-BSL 模型，兼顾了计算效率，在常规流动预测中表现良好，但缺乏在强逆压梯度下分离流动的具体研究及其与涡黏性模型的对比。本文基于Stress-BSL 模型，分析雷诺应力模型在二维驼峰（Hump）逆压梯度分离、跨声速凸块（Bump）激波-边界层干扰分离、M6 跨声速机翼三维边界层分离中的预测表现。基于模型所反映的物理现象和数学构造，对预测分离流动时出现误差的原因及机制进行分析探究。通过与涡黏性模型进行对比，预测其性能优势，为未来湍流模型的改进和优化提供参考。

1 湍流模型与算法介绍

雷诺应力模型直接求解雷诺应力输运方程，本文选取 Stress-BSL 模型作为雷诺应力模型的代表，将长度尺度ε与长度尺度ω进行混合，该模型的构造为

雷诺应力输运方程为

式中：ρ为密度；为平均速度；Reij为雷诺应力；μ为分子黏度性；μt为涡黏性系数。雷诺应力再分配项作为输运方程的重中之重，该项的构造为

式中：k为湍动能；δij为克罗内克符号；C1、α、β、γ为模式常数；Sij为平均应变率；Wij为角速度；aij为各向异性张量。Sij、Wij、aij3个参数的计算公式为

耗散项采用各向同性假设进行模化，可表示为

ω输运方程为

本文空间离散方法针对有限体积法求解采用二阶中心差分格式，针对黏性通量插值算法采用二阶迎风 MUSCL（Monotone Upstreamcentred Schemes for Conservation Laws）重构格式，无黏通量采用 HLLC（Harten-Lax-van Leer-Contact）格式。时间离散格式采用隐式LU-SGS（Lower-Upper Symmetric Gauss-Seidel）方法［15］。

2 数值计算与结果分析

2.1 二维驼峰（Hump）逆压梯度分离

二维驼峰（Hump）模型［16-17］的前半部分上凸，流道收缩，流体在此处加速，压强减小，后半部分突然下凹，流道扩张，出现较强的逆压梯度，边界层发生分离。由于驼峰下游的压力梯度接近于0，因此边界层可以再附于下壁面，分离区位于驼峰后半部分下凹位置。

图1 给出了Hump 模型的计算网格，对边界层和驼峰后半部分进行了网格加密，网格分辨率为1 633×433（流向×法向）。来流马赫数为0.1，来流总温与参考温度的比值为1.007，来流总压与参考压强的比值为1.002；出口静压与参考压强的比值为0.999 62。

图1 Hump 模型计算网格Fig.1 Calculation grids of hump

图2 给出了2 种模型计算的驼峰后缘流线和无量纲流向速度（U/U∞）分布，其中，U为当前位置流速；U∞为自由来流速度；X、Y方向位置采用弦长（c）无量纲化。可以发现分离区上缘流动存在明显的剪切，Stress-BSL 模型预测结果误差更小，具体的流动分离和再附位置如表1。但是在再附点附近可以明显地发现，Stress-BSL 模型预测的流线出现了不符合物理规律的向前弯曲，其他雷诺应力模型也被发现存在类似的问题［4］。这可能是由于雷诺应力模型在此处预测的湍流长度尺度增长率过大，导致剪切区域本应向下游发展的流线受到分离区剪切影响突然增大，出现流线弯曲。

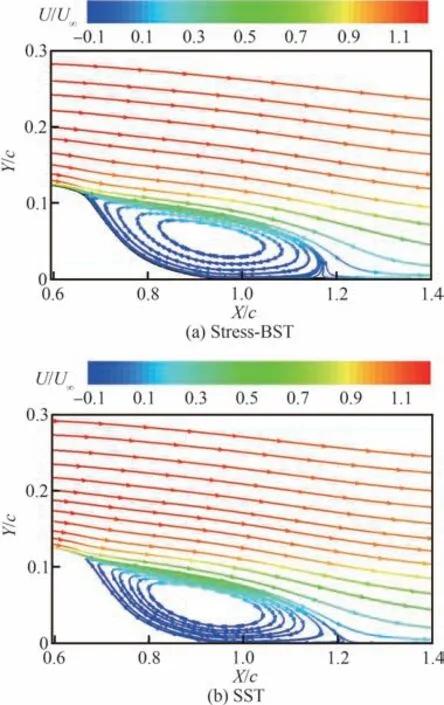
图2 Hump 模型后缘无量纲流向速度与流线图Fig.2 Nondimensional velocity and streamline behind hump

2.2 跨声速凸块（Bump）激波诱导边界层分离

跨声速凸块（Bump）流动模型［18］由一个环形圆弧凸起构成，气体流经凸起速度增加产生激波，在凸起的后半部分发生激波诱导分离，随后边界层再附并在凸起后缘产生分离区。图3 给出了轴对称跨声速凸块的计算网格，对边界层、激波和环形凸块后缘部分进行了网格加密，网格分辨率为721×321（流向×法向）。为模拟轴对称条件，需将二维平面网格绕X轴旋转1°，并将横向边界面设置为周期边界。来流马赫数为0.875，来流单位雷诺数为2.76×106m−1。

图3 Bump 模型计算网格Fig.3 Calculation grids of bump

图4 Bump 模型后缘无量纲流向速度与流线图Fig.4 Nondimensional velocity and streamline behind bump

2 种模型预测所得流场流线和无量纲流向速度（U/U∞）分布见图 4，可以明显地发现 SST 模型预测的流动再附点位置过于靠后，分离区过长，具体的流动分离点和再附点位置见表2。2 种模型的计算结果均出现了流动分离点提前，但Stress-BSL 模型的误差更小。对于再附点，SST 模型预测的结果靠后，而Stress-BSL 模型的结果则较实验值靠前。由于凸块模型高度较小，再附点附近流线曲率很小，因此前述的原因导致流线向前弯曲，易使流动提前再附。整体来看 Stress-BSL 模型预测效果更好。

表2 Bump 模型分离、再附点位置Table 2 Separation and reattachment points of bump

表3 网格无关性验证Table 3 Grid independence verification

2.3 跨声速 M6 机翼三维边界层分离

ONERA M6 机翼是跨声速三维激波诱导边界层分离的经典算例［19］。在跨声速来流条件下，机翼的上表面会出现激波，并且由于三维边界层存在展向流动，在靠近翼尖的区域激波增强并出现激波诱导分离。研究表明，2 种湍流模型对于小攻角下的流动预测均与实验吻合良好，因此本文采用大攻角6.06°进行强激波诱导分离的预测能力对比，来流马赫数为0.84，来流单位雷诺数为1.46×107m−1。

图5 给出了跨声速三维 ONERA M6 机翼模型的计算网格，采用 O-H 型拓扑，由于没有侧滑角，故采用半模进行计算，并对边界层、机翼前缘部分和机翼翼尖段进行了网格加密，总共设计了粗、中、细、极细4 种网格，半模网格量分别约为133 万、265 万、530 万、795 万，网格细节见表 3。

图5 M6 计算网格Fig.5 Calculation grids of M6

图6 为采用 Stress-BSL 湍流模型计算的4 套 ONERA M6 机翼网格在6.06°攻角下20%展长位置处的压力系数（Cp）分布计算结果与实验值的对比结果。发现细网格和极细网格对激波位置的捕捉基本一致，且与实验值误差较小，为节省计算资源，后续均采用细网格进行数值模拟。

图6 网格无关性验证Fig.6 Grid independence verification

图7、表4 给出了2 种湍流模型的计算结果对比。由图7（a）、图7（b）可以发现，在机翼的背风面存在明显的“λ”型激波。对比2 种模型的预测结果，Stress-BSL 模型预测的激波结构更为合理。对于激波诱导边界层分离而言，波后高压前传导致波前边界层增厚，流动受阻进一步导致了激波的增强，因此流动分离的位置与激波位置几乎重合。随着逐渐靠近翼尖，激波增强，Stress-BSL 模型预测的结果始终与实验值符合较好，而 SST 模型预测的激波位置开始前移，分离区过大（见图7（c）），与实验值的误差增大。过大的分离区导致流动再附受阻，在机翼尾缘附近压力系数明显偏大（见图8）。需要注意的是，图8（a）、图8（b）中Stress-BSL 模型预测的激波位置反而较SST 模型误差偏大。这是由于风洞实验中翼根平面并不是对称面，而CFD 计算中将翼根平面设置为对称面，因此产生了边界条件干扰，使得激波预测位置较实验值后移。但由于SST 模型预测的激波位置靠前，因此导致了图8（a）、图8（b）的SST 模型预测激波位置更准的巧合性结果。这种边界条件干扰会随着逐渐远离翼根平面而消失。Rumsey［4］研究也提到了这一点。

表4 升力系数与阻力系数对比Table 4 Comparison of lift and drag coefficient

图7 不同湍流模型计算结果对比Fig.7 Comparison of simulation results with different turbulence models

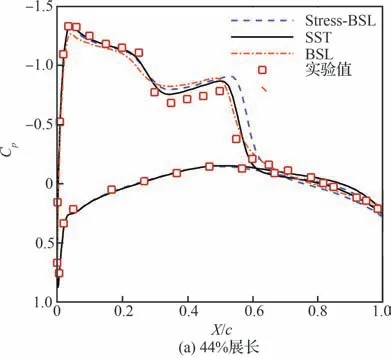
图8 不同站位压力系数Fig.8 Pressure coefficient at different stations

另外，由于Stress-BSL 模型预测的流动分离更加准确，分离区更小，背风面后缘的压力系数较SST 模型的预测结果更小，使得机翼上下表面间的压强差更大，且压差阻力更大，因此相较于SST 模型的预测结果，升力系数和阻力系数均更大（见表4）。

3 湍流模型性能机制

基于计算结果，本节着手从湍流模型的构造机制出发，探明预测分离点提前、再附点滞后、分离区过大的具体原因。雷诺应力的物理含义为流体微元表面上脉动动量输运的平均值，可以认为对于湍流边界层而言，更小的雷诺应力意味着边界层抵抗逆压梯度的能力越差，越容易出现流动分离。因此，湍流模型对雷诺应力的预测能力直接决定了对分离流动预测的准确性。

3.1 Stress-BSL 模型

图9 给出了Hump 模型、Bump 模型特点站位的Stress-BSL 模型雷诺应力计算值与风洞实验值对比。可以发现，Stress-BSL 模型的预测值较实验值偏低，导致了预测分离提前和再附滞后。虽然通过直接描述雷诺应力的输运过程避免了引入假设的误差，但雷诺应力输运方程中难以实验观测和模化的项，给建模带来了未知性和误差，使得 Stress-BSL 模型虽然具有优势，但仍存在较大误差。分析雷诺应力输运方程中的各项，可以得到 Stress-BSL 模型预测不准的原因。

图9 Stress-BSL 模型雷诺应力计算结果与实验值对比Fig.9 Comparison of stress-BSL and experimental Reynolds stress

1）生成项

由于雷诺应力模型直接求解雷诺应力输运方程，因此可以对生成项精确求解。但精确并不是绝对准确，在求解雷诺应力时由于模型建模误差导致的计算误差会发生累积。因而，所谓的精确是指在生成项求解过程中没有引入新的变量和假设，不会产生新的误差。

2）扩散项

Stress-BSL 模型中扩散项将雷诺应力的扩散速率与其在流场中的梯度表示为正比。De‐muren 和Sarkar［20］通过对平面通道湍流研究后发现：扩散项在对数层对雷诺正应力的计算结果影响不大，但可以对边界层外层湍流转化为各向同性产生影响。这一项并不是雷诺应力模型预测带有强烈剪切的分离流动准确与否的决定性因素，绝大多数文献并未对其影响进行专门研究。

3）耗散项

湍流耗散的情况十分复杂，包括由大涡和小涡拉伸、压强作用、湍流输运、分子扩散造成的耗散作用，以及湍动能耗散自身的耗散作用。由于耗散作用基本发生在湍流的最小尺度中，此时的耗散作用除近壁区等特殊区域外，可以认为是各向同性的。Stress-BSL 模型中扩散项采用了各向同性的耗散模型［21］。由图9 也可以发现，在近壁区雷诺应力的计算值和实验误差很小，因此该假设基本合理。但需要注意的是，耗散项中的模式封闭参数事实上需要根据雷诺数不同进行经验修正，在不同的流动区域内取值不同，且耗散项与湍流长度尺度息息相关，对雷诺应力模型的预测能力影响较大。

4）再分配项

雷诺应力再分配项是脉动压强和应变率张量相关的平均值［22-24］。由于湍动能输运方程中并不存在再分配项，说明再分配项对于湍动能的产生没有贡献，而只是在湍流脉动速度的各个分量之间进行调节。不同于扩散作用依赖于明确的梯度，再分配项是一种能量转移，通过将量值较大的速度分量转移给量值较小的速度分量，以达到各方向分量的平衡。为明确其作用，给出二维湍流场的雷诺应力输运方程

可以发现，Y方向的雷诺正应力生成项为0。假设在均匀剪切场中初始时只有正应力，没有切应力。由于流场的剪切作用，雷诺切应力开始增长，导致X方向正应力的生成项大于0，X方向正应力开始增长。但Y方向的雷诺正应力生成项为0，这将使得Y方向正应力被耗散进而导致切应力生成项消失。再分配项则可以将X方向分量的一部分能量转移给Y方向，使其保持一定强度，从而保持了切应力的生成和强度，形成了一个维持湍流场的闭环机制。由于再分配项的重要作用，同时与生成项有相同的量级，且缺乏模化依据，因此是预测误差的主要来源。Stress-BSL 模型将其表示为快速和慢速项之和。快速项中包含平均速度梯度，这说明雷诺应力再分配不是局部过程，不能仅取决于当地一点的参数。但模型构造却基于同一物理位置的湍流波动量的相关性完成模型闭合，这会导致一部分湍流信息的丢失，使得快速项的建模失准，在速度梯度越大的区域，误差也会越大。图9 的结果证明，在边界层内剪切最强烈（速度梯度大）的区域，雷诺应力计算值与实验值误差最大。其中，图中纵坐标Y−Y0、Z−Z0分别为Hump 模型和Bump 模型的当地壁面法向距离，并使用弦长进行无量纲化。由于边界层外侧的速度梯度小于内侧，因此边界层内侧的雷诺应力预测误差远大于外侧。另外，当前快速项的模化是基于快速畸变近似，非线性模型可认为是利用张量函数性质在原线性模型中添加了各项异性张量的二次项［25］，而不是在物理现象层面的对流动信息的补充。

3.2 SST 模型

相较于雷诺应力模型，涡黏性模型对雷诺应力的求解是基于Boussinesq 假设，通过涡黏性系数（μt）完成的，因此SST 与Stress-BSL 模型对分离流动预测失准的原因大相径庭。SST 湍流模型的具体构造细节可参见文献［26］。

1）流动分离

起初的两方程模型（k-ε模型、k-ω模型）对于逆压梯度的预测能力很大程度上局限于边界层对数区域［27-29］，预测效果并不好。Menter 和Egorov［14］发现边界层尾迹区域的涡黏性水平最终决定了涡黏性模型对逆压梯度流动的预测能力，因此在构造SST 模型时引入了 Bradshaw 假设，在涡黏性系数表达式中强制保证湍流剪切应力与边界层尾迹区的湍动能成正比，从而获得了很好的附着流和弱逆压梯度流动的预测结果。其中涡黏性系数表达式为

对于存在很大速度梯度剪切很强的边界层内，涡黏性系数的表达式中分母则由平均应变率（S）代替，使得湍动能生成项保持与耗散项相等，这也对应了Bradshaw 假设中包含的湍流能量平衡。但对比雷诺应力计算结果与实验值（见图10），显然模型对于雷诺应力的限制过度了，导致雷诺应力预测值较实际情况偏小。这是由于Bradshaw 假设是通过Klebanoff 零压力梯度平板边界层试验数据总结得出的［30］，其基础为无压力梯度的附着流动，当逆压梯度非常大时，流动的平均应变率很高，使得湍动能生成项明显大于耗散项，但 SST 模型中的控制器限制其生成项仍等于耗散项，使得湍动能和涡黏性系数小于真实值，造成了预测的雷诺应力偏小。

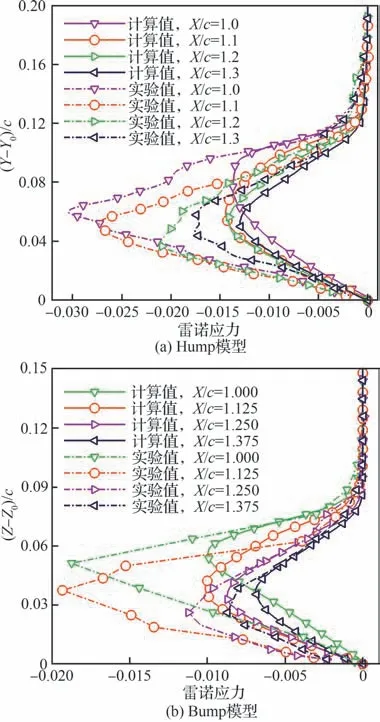
图10 SST 模型雷诺应力计算结果与实验值对比Fig.10 Comparison of SST and experimental Reyn‐olds stress

还需要注意的是，基于二维平板边界层数据提出的Bradshaw 假设在推广到三维边界层时引入了“主雷诺应力”的概念，将三维边界层内雷诺应力张量其他各向分量的变化描述为对主雷诺应力的变化的贡献。但在强逆压梯度下，雷诺切应力各方向分量（UV、VW、UW Stress）间的差值很小，雷诺正应力（UU、VV、WW Stress）与切应力达到同一量级（见图11）。显然主雷诺应力的的概念不再成立。

图11 雷诺应力对比Fig.11 Reynolds stress comparison

考虑到BSL 模型与SST 模型的构造基本相同，唯一区别在于BSL 模型未对湍动能生成项进行限制，因此可以通过BSL 模型，对基于Brad‐shaw 假设的控制器所带来的影响进行对比分析。通过BSL 模型与SST 模型的计算结果对比（见图8、图12），发现 BSL 模型的计算结果不同程度上抑制了流动分离的提前，证实了上述分析的SST 模型预测失准的原因。

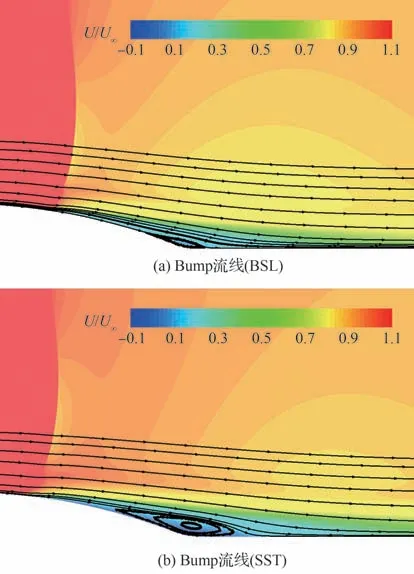
图12 BSL 与SST 模型计算结果对比Fig.12 Comparison of BSL and SST models

究其原因，是因为涡黏性模型所基于的Boussinesq 假设包含的线性关系、各向同性等“先天缺陷”，导致了涡黏性模型在预测存在突然的平均应变率变化、额外应变率和明显的各向异性等特征的流动时出现失准。

2）流动再附

如上所述，SST 模型对边界层雷诺应力的低估导致了流动分离的提前。相应的，湍流模型对分离区上缘与主流之间的雷诺应力的预测则影响了流动的再附位置的计算结果［31］。由于雷诺应力表征脉动动量的输运，因此在分离区上缘预测的雷诺应力越大，动量输运越多，湍流能量越高，流动再附位置越靠前。相反地，预测的雷诺应力越小，则流动再附位置的计算结果越靠后。考虑到SST 模型中雷诺切应力主要由涡黏性系数（μt）和平均应变率（S）决定。因此希望通过对比 Stress-BSL 模型与 SST 模型的计算结果找出主要影响因素（见图13、图14）。

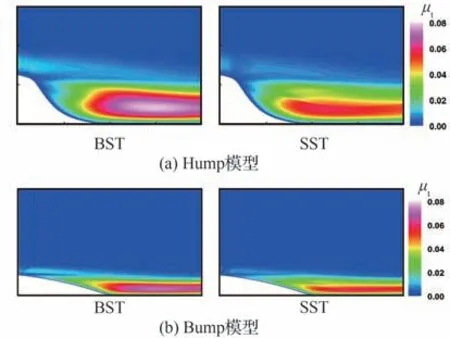
图13 涡黏性系数对比Fig.13 Comparison of eddy viscosity coefficient

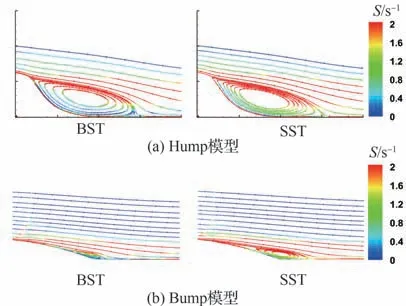
图14 平均应变率对比Fig.14 Comparison of mean strain rate

发现相较于Stress-BSL 模型，SST 模型预测的μt偏小，S则偏大，但图9、图10 的结果表明SST 模型预测的雷诺应力更小。据此推测，相较于S，μt的计算结果对于雷诺应力的预测影响更大。考察计算μt的SST 模型输运方程，由于雷诺应力被低估，导致湍动能输运方程的生成项被低估，扩散项同样偏小，上述共同作用使得湍动能k偏小，但表达式为隐式，影响较为复杂。对于比耗散率ω，利用量纲分析，可以得到湍流特征长度尺度δl的表达式

发现δl与ω之间为倒数关系。由于雷诺应力表征湍流内的动量输运，因此雷诺应力的预测与湍流能量紧密相关，而湍流能量又与湍流长度尺度直接相关。因此雷诺应力被低估，说明湍流能量和长度尺度被低估，则ω被高估。考虑ω输运方程，则耗散项同样会被高估，这就要求生成项偏高更多，由于已经分析过湍动能生成项被低估，因此可以认为几乎完全由位于分母位置的μt导致了ω生成项被高估。这说明，虽然k、ω输运方程相互耦合，且均与μt相关，但显然μt、ω的相互影响更为直接。据此推测，与ω相关的模型长度尺度的建模失准、忽略耗散过程的各向异性特征是造成μt预测结果偏小的主要原因。

3）关键参数再标定

基于Bradshaw 假设的限制器强制湍动能生成项与耗散项相等，使得SST 模型低估了雷诺应力，但该假设丰富了模型的物理信息，因此并不能直接摒弃该假设。Zhao 等［32］研究后发现，系数a1对于分离激波具有很高的敏感度，并且a1是激波诱导分离的分离区内压力系数不确定性的主要来源，因此可以通过增大a1放宽对雷诺应力的限制。经过试算，发现a1=0.35 可以取得相对满意的结果。

由图15 可以发现，对a1进行调整可以在一定程度上取得更加接近实验数据的结果，再标定后的模型对于M6 机翼的背风面激波预测更加合理，两道激波合并为一道的位置向翼尖移动，且合成后的强激波的位置向下游移动。由壁面流线可以发现再标定后模型预测的分离区更小，没有出现分离起始位置过于靠近翼根位置的现象，整体对激波位置的捕捉和激波后区域的压力系数的预测均更为准确。

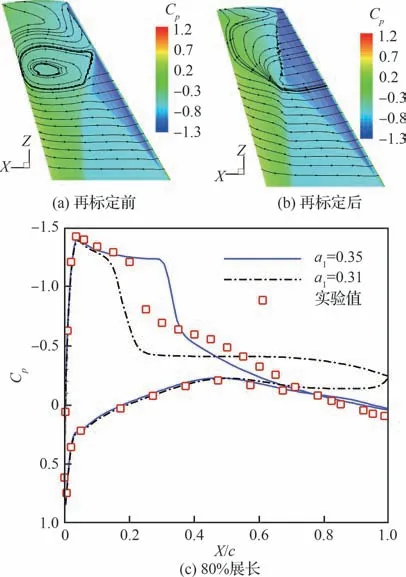
图15 a1标定前后压力对比Fig.15 Comparison of pressure with different a1

4 结论

经过试算，对比筛选后选用了SST 模型、Stress-BSL 模型作为涡黏性模型和雷诺应力模型的代表对湍流分离流动进行了计算。选取了NACA4412 翼型、二维驼峰、二维跨声速凸块、跨声速三维ONERA M6 机翼，从数学构造和物理现象等方面入手对这2 个湍流模型的分离流动的预测性能进行了对比，给出了较为深入的机制分析，并基于分析所得原因对模型进行了常数再标定，提出了改进方向，得到如下主要结论：

1）对于强逆压梯度下的分离流动，Stress-BSL 模型和SST 模型均出现预测失准，但Stress-BSL 模型的预测结果与实验值误差更小、性能更好。在激波诱导边界层分离的复杂流动中，Stress-BSL 模型预测的激波特征和压力系数均与实验值吻合较好，而SST 模型则明显预测分离区过大。在三维边界层分离中，物理基础更加可靠的Stress-BSL 模型的计算结果与实验值误差很小，而SST 模型计算的压力系数与雷诺应力则与实验值偏差较大。

2）Stress-BSL 模型对分离流动预测的结果存在误差，主要是由于雷诺应力再分配项的模化不准确，其基于快速畸变近似和张量函数性质，缺乏与实际物理过程的联系。雷诺应力输运方程中耗散项同样复杂，影响重要但程度不如再分配项。其他如扩散项等对雷诺应力计算的影响不大。另外，计算中发现，数值稳定性仍是雷诺应力模型亟待解决的问题，对条件要求较为苛刻，需根据其特点开发相应的数值方法。

3）SST 模型对分离流动预测的结果取决于对雷诺应力的模化。分离提前是因为基于Brad‐shaw 假设的控制器，使得本应远大于耗散项的湍动能生成项被限制，导致雷诺应力预测偏低。而耗散尺度建模失准导致的主导雷诺应力预测结果的涡黏性系数被低估则是再附滞后的主要原因。

4）对于流动分离提前的问题，本文通过对湍动能生成项限制放宽后，预测结果得到改善。另外，涡黏性模型对分离流动计算不准的问题很大程度上可以通过对湍流尺度的建模进行改善。对于湍流各向异性特性的补充，则应聚焦于对雷诺应力本构关系添加非线性项进行修改。

5）模型的长度尺度对预测准确性起到关键作用，可以在消除边界奇性的基础上，补充对长度尺度的控制，以获得更好的预测结果。