美式蝶形期权期望的半参数界

艾晓辉 白瑞杰 刘宗昊

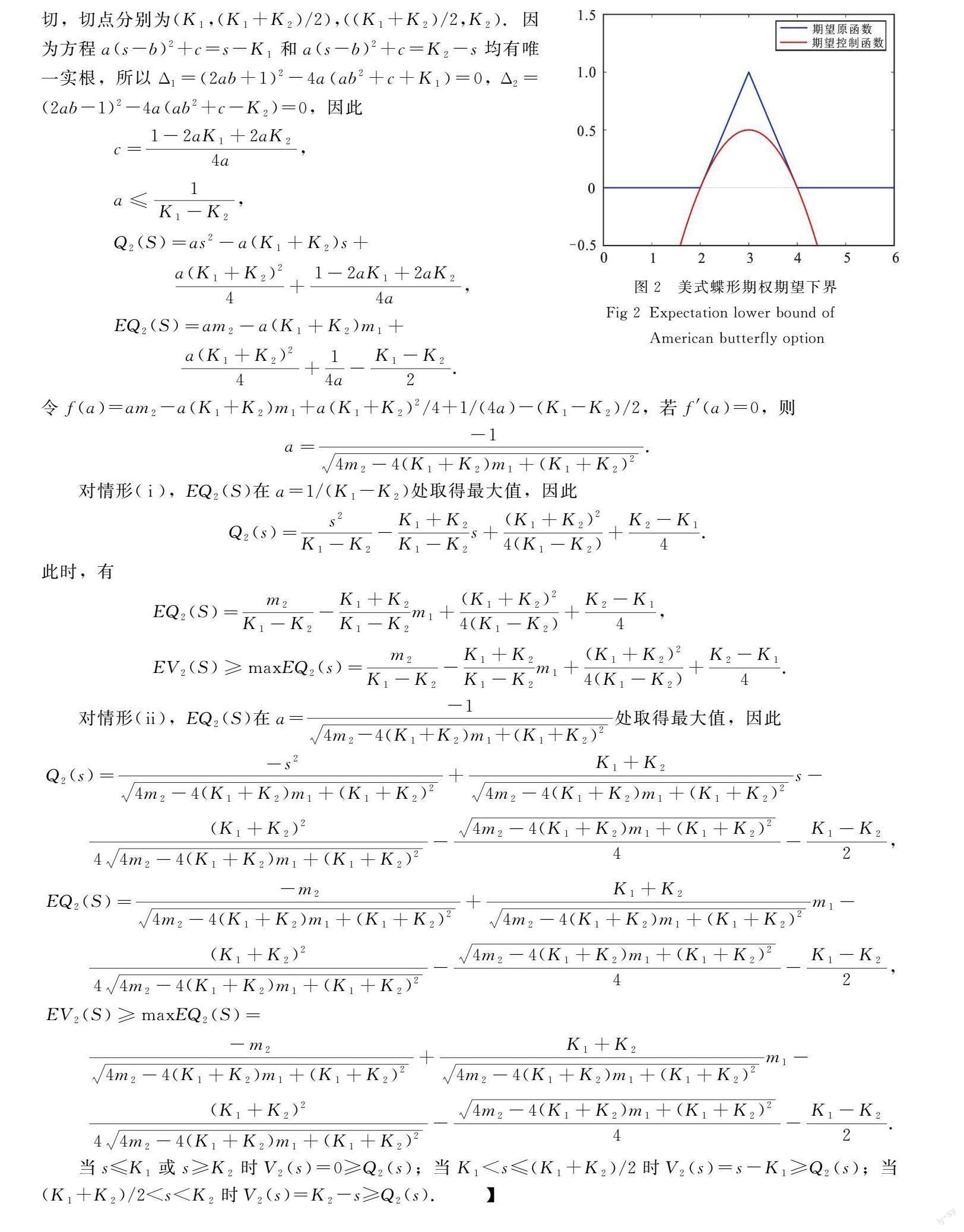
摘要：研究美式蝶形期權均值的半参数界估计问题.在给定风险资产（股票）价格的某些矩信息条件下，通过对偶方法得到美式蝶形期权的上、下矩界；利用对偶原理、测度变换和控制函数分别估计了单峰和双峰情形下美式蝶形期权期望的上界.

关键词：单峰分布；对偶原理；控制函数；半参数界；美式蝶形期权；矩问题

中图分类号：O 211.5 文献标志码：A 文章编号：1001-988Ⅹ（2023）04-0035-10

矩问题是指在给定随机变量的一定矩信息条件下，求得随机变量函数期望、方差和协方差的最优上下界问题.矩界的研究是由经济学、运筹学、概率论、统计学、期权定价、医学影像分析等领域自然产生的实际问题驱动的.矩问题可以用来估计随机规划的误差界，提供对于欧式期权、稳健估计和股票价格等金融产品的风险评估［1，2］.矩问题在现实中有广泛的应用［3-9］.

随机变量的矩估计有着悠久的历史.在不完全市场条件下的期权价格上、下界的估计问题是一类特殊的切比雪夫不等式问题.1995年，Scarf［10］研究成本控制问题时得出了一类切比雪夫型不等式，Lo［11］将Scarf的方法应用于欧式期权的收益函数;1995年，Smith［12］用Lo的上界做决策分析时提出了一类广义切比雪夫不等式.1996年，Pintelon等［13］证明了多参数模型的最小方差估计.之后，Rao等［14］提出了切比雪夫不等式在二阶矩研究中的应用，Ageel［15］从离散的α－单模态分布中得到了概率不等式的估计和二阶矩的一个上界.2008年，Zuluaga等［16］研究了欧式期权在给定的三阶矩条件下的上、下界.2010年，Sharma等［17］给出了有限维空间方差的界估计.

4 结论

本文利用对偶方法和测度变换研究了美式蝶形期权的矩界，得到了期权期望的上、下界，同时给出了期望上界的可达结果.另外，分别给出了单峰和双峰情形下美式蝶形期权期望的上界.

参考文献：

［1］ DOKOV S P，MORTON D P.Second-order lower bounds on the expectation of a convex function［J］.Mathematics of Operations Research，2005，30（3）：662.

［2］ MALLIAVIN P.Integration and Probability［M］.New York：Springer Science and Business Media，1995.

［3］ DASPREMONT A，GHAOUI L E.Static arbitrage bounds on basket option prices［J］.Mathematical Programming，2006，106（3）：467.

［4］ BERGER B.The fourth moment method［J］.SIAM Journal on Computing，1997，26（4）：1188.

［5］ CHUNG K L，FARID A.Elementary Probability Theory［M］.New York：Springer，2010.

［6］ COURTOIS C，DENUIT M.Moment bounds on discrete expected stop-loss transforms，with applications［J］.Methodology and Computing in Applied Probability，2009，11（3）：307.

［7］ PACHPATTE B G.New bounds on certain fundamental integral inequalities［J］.Journal of Mathematical Incqualitics，2010，4（3）：405.

［8］ POPESCU I.A semidefinite programming approach to optimal-moment bounds for convex classes of distributions［J］.Mathematics of Operations Research，2005，30（3）：632.

［9］ SCOTT A，FRANCOIS W.Goal achieving probabilities of constrained mean-variance strategies［J］.Statistics and Probability Letters，2011，81（8）：1021.

［10］ SCARF H.A Min Max solution of an inventory problem［J］.Proceedings of the Fujihara Memorial Faculty of Engineering Keio University，1959，12：114.

［11］ LO A W.Semi-parametric upper bounds for option prices and expected payoffs［J］.Journal of Financial Economics，1987，19（2）：373.

［12］ SMITH J E.Generalized Chebychev inequalities：theory and applica tions in decision analysis［J］.Operations Research，1995，43（5）：807.

［13］ PINTELON R，SCHOUKENS J，MCKELVEY T，et al.Minimum variance bounds for overparameterized models［J］.IEEE Transactions on Automatic Control，1996，41（5）：719.

［14］ RAO B P，SREEHARI M.Chernoff-type inequality and variance bounds［J］.Journal of Statistical Planning and Inference，1997，63（2）：325.

［15］ AGEEL M.Variance upper bounds and a probability inequality for discrete α－unimodality［J］.Applicationes Mathematicae，2000，27（4）：403.

［16］ ZULUAGA L F，PEA J，DU D.Third-order extensions of Los semiparametric bound for European call options［J］.European Journal of Operational Research，2009，198（2）：557.

［17］ SHARMA R，GUPTA M，KAPOOR G.Some better bounds on the variance with applications［J］.Journal of Mathematical Inequalities，2010，4（3）：355.

［18］ KHINTCHINE A Y.On unimodal  distributions［J］.Izv Nauchno-Isled Inst，1938，2：3.

［19］ ROBERTSON C A，FRYER J G.Some descriptive properties of normal mixtures［J］.Scand Actuar Tidskr，1969，52：137.

（責任编辑 马宇鸿）