改进D*算法下的无人机三维路径规划

汪小帅,朱其新,朱永红

(1.苏州科技大学 电子与信息工程学院,江苏 苏州 215009;2.苏州科技大学 机械工程学院/建筑智慧节能江苏省重点实验室/苏州市共融机器人技术重点实验室,江苏 苏州 215009;3.景德镇陶瓷大学 机电工程学院,江西 景德镇 333001)

0 引 言

近年来,随着无人机在军事、工业和生活等多个领域内的广泛应用,无人机的自主飞行能力要求越来越高。路径规划作为无人机飞行高效、稳定、安全和自主地完成任务的关键技术,一直是国内外相关技术领域学者的重点研究对象之一。

无人机路径规划[1-2]问题的本质在于根据先验知识和无人机所需完成的任务,在三维环境下找到一条从起始点到目标点的安全无障碍路径。目前,三维路径规划算法可分为传统算法和智能算法2大类。传统算法包括RRT算法[3-4]、人工势场法[5-6]、A*算法[7-8]等;智能算法有遗传算法[9-10]、蚁群算法[11-13]、神经网络算法[14]、粒子群算法[15]等。文献[3]在RRT算法中引入目标点为导引点的启发函数,同时设置动态扩展步长,解决了算法用作三维路径规划时易出现效率低下以及路径冗长、不平滑等问题。文献[7]结合无人机物理约束和环境威胁约束建立数学模型,并以此提出一种基于模型约束的改进A*算法。文献[9]在遗传算法中引入差分进化变异策略,并结合模拟退火算法,加强遗传算法变异的多样性,避免陷入局部最优。文献[11]结合蚁群算法和人工势场法,提出一种新的信息素更新机制,并改进启发函数,算法收敛速度显著提高。文献[14]应用传统算法规划路径,同时采用强化学习训练无人机避障,无人机动态避障能力得到显著提高。

相较于上述算法,D*算法在面对动态障碍物以及寻找安全路径方面一直有着良好表现,尤其与基于强化学习、深度学习的智能算法相比,D*算法不需要庞大的训练数据和漫长的训练时间,且不必担心所得路径会受训练数据的影响。但传统D*算法在用作路径规划时也经常出现搜索效率低以及路径复杂性高等问题。文献[16-18]将全局地图环境分解为多个局部环境,优化子节点的选取方式,同时改进代价函数并引入平滑函数,所得路径复杂性有所降低。文献[19-20]改进有向D*算法,引入关键节点逐级搜索,改善移动机器人路径规划的性能。但这些方法一般运用在二维环境中。针对三维环境中遇到的问题, 文献[21]先采用卡尔曼滤波算法预测目标位置,然后使用算法完成路径规划,虽然有效缩短航程,但路径复杂性依旧很高。文献[22-23]结合遗传算法提出一种不同的改进方案,根据特定策略从D*算法规划的初始航迹中提取特征点路径,并以此生成初始种群,设计适应度函数。但在方向约束下的D*算法会产生大量无用节点。

以上方法在一定程度上改进了传统D*算法的搜索效率和规划路径。但传统D*算法在实际用作路径规划时依然存在一些弊端:①规划阶段计算量大,算法效率不高;②所得路径总是长于实际可到达目标点的路径,冗余节点过多。针对这些问题,本文提出一种改进的D*算法,该算法采用变步长的方式扩展节点,同时利用切比雪夫距离和曼哈顿距离的融合式(切-曼融合式)作为代价值,并对算法所得路径进行优化处理,保存关键节点,删除冗余、不必要的路径点。

1 D*算法理论

D*算法的核心代价函数[24]:

F(n)=G(n)+H(n)

(1)

式中:n为当前节点;G(n)为当前所在节点到起始点的实际代价值;H(n)为当前所在节点到目标点的代价估计值。

D*算法的代价估计值H(n)可以具体表达为

式中:Succ(n)为当前节点n的扩展节点集合;n′为当前所在节点n的扩展节点;T为目标节点;H(n′)为n′的代价估计值;C(n,n′)为2个相邻节点的代价值。

D*算法在三维环境下进行路径规划时,会创建OPEN表和CLOSED表来完成扩展节点和选取最优节点的任务。从目标点栅格开始,对目标点栅格周围的26个栅格节点进行搜索并存入OPEN表,然后计算它们的代价值和代价估计值,选取最优的栅格节点(代价值最小的栅格节点)继续扩展,被扩展过的点从OPEN表中删除,存入CLOSED表中。重复上述操作,依次扩展节点,直到起始点从OPEN表中删除,执行过程如图1所示。

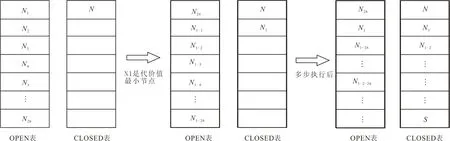
图 1 OPEN和CLOSED表执行过程Fig.1 The execution of the list OPEN and list CLOSED

图1中,当遍历到当前栅格节点N时,将节点N存入CLOSED表,遍历该栅格周围的26个栅格并存入OPEN表;经过代价函数计算,将代价值最小的栅格节点N1从OPEN表中删除,存入CLOSED表中。然后遍历节点N1周围的26个栅格节点,计算出最小的代价值节点N1-2从OPEN表中删除,存入CLOSED表中。之后继续向前遍历,直到起始点S存入CLOSED表中。

2 D*算法的改进

传统D*算法在搜寻无障碍路径时,通常因为规划阶段的庞大计算量以及生成路径复杂性高等问题导致算法效率低下,本文对传统D*算法提出以下改进。

2.1 扩展节点选取

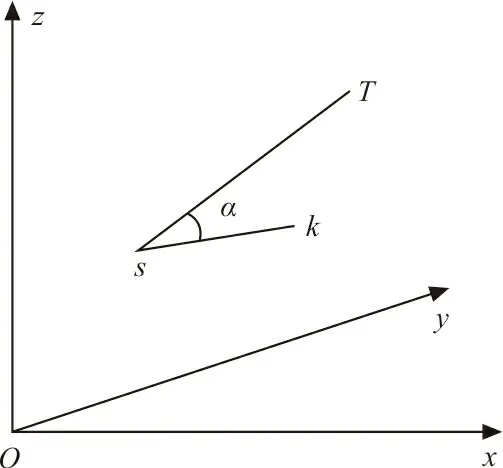
在三维环境下,传统D*算法以当前栅格为基准,选择其相邻的26个栅格作为扩展节点。本质是从当前栅格出发向,以步长为1,向x、y、z方向(可以反方向)进行遍历。当地图模型较大,起始点和目标点跨越整个地图时,需要耗费大量的时间去遍历节点选取路径。本文采用变步长的方式,根据扩展栅格节点(xR,yR,zR)和目标点栅格(xT,yT,zT)的位置关系定义步长h,当扩展节点栅格未到目标点栅格时,加快遍历速度,步长较大;当扩展节点栅格超过目标节点栅格,则选取较小的步长;以x方向为例,具体实施如下:

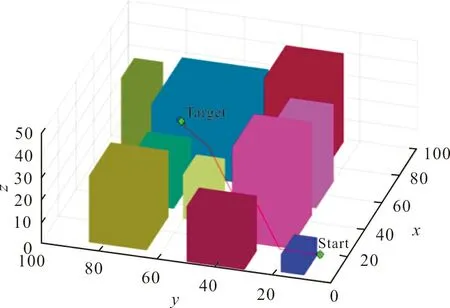
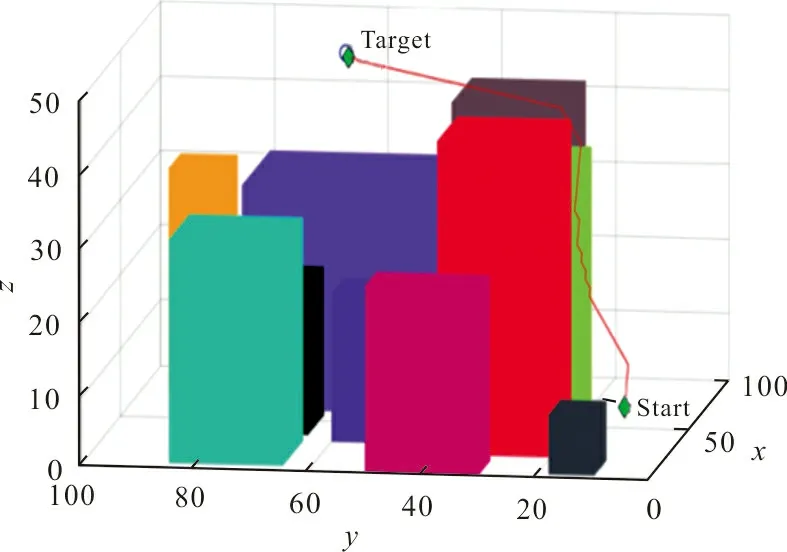
①当xR

(3)

②当xR>xT时,步长h为-1。

同理,y方向与z方向也采用同样的方法。这样的方式在加快遍历速度的同时,保证路径的精确性、安全性。

2.2 代价函数优化

传统D*算法采用欧氏距离作为代价值的计算需要进行开方运算,使得算法整体的计算量较大,在规划阶段选取代价值最小节点时,这一特点会导致算法效率低下。尤其在三维环境下,还需要考虑高度因素,从而使欧氏距离的计算复杂度成倍增加。

综上所述,本文对代价函数中代价值的评判依据做出了优化,用切-曼融合式替代了传统欧氏距离。将当前节点、目标点所在直线与当前节点、扩展节点所在直线的夹角值定为α,如图2所示,并将sin α作为切比雪夫距离和曼哈顿距离融合的权重值,得到距离融合式如下:

d=sin α·dc+(1-sin α)·dm

(4)

式中:dc为三维空间内两点间切比雪夫距离;dm为三维空间内两点间曼哈顿距离。

图 2 权重夹角Fig.2 Weight angle

图2中,s为当前节点,k为扩展节点,T为目标点,直线sT与直线sk夹角为α∈(0°,90°)。当夹角α趋向于0°时,s、k、T应三点共线,代价距离近似于曼哈顿距离较为精确;当夹角α接近直角时,代价距离近似于切比雪夫距离为最优。

2.3 路径优化

传统D*算法找到的无障碍路径常常会存在不必要的拐点,这会导致生成的路径长于实际可到达目标点的路径。为提高无人机的效率,本文对已生成的路径进行优化处理,将一些冗余的拐点剪除。

路径优化过程从目标点开始,将目标点设置为第1个判断点,依次遍历前面的路径节点并判断当前遍历的节点与判断点之间的连线是否穿过障碍物,如果不穿过障碍物则继续向前遍历路径节点;如果穿过障碍物,则将当前遍历到的节点的后一个节点更新为判断点,继续向前遍历判断,直到判断点与起始点的连线不穿过障碍物,如图3所示。

图 3 路径优化过程Fig.3 Path optimization process

从图3可以看出,从目标点T开始向前优化路径,将目标点T作为第一个判断点。目标点T与点p1之间的连线不会穿过障碍物;继续向前遍历路径点,发现目标点T与点p2连线发现也不会穿过障碍物,此处可以删除多余路径点p1;继续向前遍历路径点,目标点T与点p3连线穿过了障碍物,所以不能优化出目标点T直达点p3的路径,将点p3的后一点p2更新为判断点,从点p2开始继续向前遍历判断,优化整条路径。

上述优化路径的过程中,如何在三维环境下判断两点之间的连线是否穿过障碍物是问题的关键,其本质是判断空间内两点间线段是否与立方体有交点。如果采用在三维空间内直接判断的方式,计算量较大且在栅格边缘处难以判断清楚。本文采用投影法,将三维路径及三维障碍物地图投影到二维平面上,然后根据路径段投影与障碍物投影间的关系判断路径段是否穿过障碍物,如图4所示。

(a) 路径与障碍物的二维投影

由此可得,路径段p5p6所在直线与平面的夹角θ的正切值为

另一方面，组织与组织之间操作化为组织与媒体、组织嵌入方式和组织与国家、民间、企业三个方面。媒体的介入起到的效果是双方面的，大众传媒有利于整个社工行业的宣传和监管，而在整个社会对社工职业的认知都尚处于初级阶段，社工组织自身的能力仍需不断提升的情况下，是需要谨慎看待媒体的介入，例如双方在理念上差异而导致服务对象的权益受到损害。后两者可以从影响力来看，即目前外界给予社工职业的影响力量较强，而反之社工对于外界的影响力较弱。

路径段p5p6上任意一点q的高度qq′为

若qq′小于z,则说明在三维环境下,路径段p5p6穿过障碍物O1。

2.4 改进D*算法的实现

改进D*算法的执行过程如图5所示。

3 仿真实验和结果分析

3.1 环境模型和无人机动力学模型

本文使用MATLAB作为实验平台进行仿真实验。为验证算法改进结果的有效性,将传统D*算法和改进后的D*算法进行对比仿真实验。三维城区场景设置如图6所示。

图6中,Start所在位置为起始点,Target所在位置为目标点,其余立方体表示城区楼房建筑,属于障碍物,白色区域表示无人机可以自由行驶的区域。从起始点出发,选择一条到达目标点的无障碍路径,从而完成路径规划。

本文主要研究四旋翼无人机的动力学模型[25]。在无人机的飞行过程中,可以将动力学系统划分为3个子系统,即高度子系统、偏航子系统和水平位置子系统。针对这3个子系统,本文建立如下动力学模型,以验证改进后的D*算法是否符合无人机的动力学要求。

式中:子系统∏1主要控制无人机的升降运动;子系统∏2负责控制无人机的朝向和转向运动,子系统∏1和∏2均属于全驱动系统;子系统∏3则主要负责控制无人机的水平飞行运动,属于欠驱动系统。由于系统存在建模不确定性,本文假设无人机转动惯量J1、J2、J3、空气动力学参数Ki(i=1,2,…,6),无人机重心与螺旋桨轴心之间的距离l以及力-力矩比例常数c均为未知常数。

由于四旋翼无人机在飞行过程中不会做出过大机动动作,本文提出如下合理假设:四旋翼无人机的俯仰角θ(t)和滚转角φ(t)满足以下不等式

-π/2<θ(t)<π/2,-π/2<φ(t)<π/2

(10)

3.2 仿真实验

为验证本文采用切-曼融合式作为代价值的优越性,将改进后D*算法与使用切比雪夫距离或曼哈顿距离作为代价值的D*算法进行对比实验,结果如图7所示。

(a) 切比雪夫距离作为代价值的D*算法

从图7可以看出,采用切-曼融合式有效避免了使用切比雪夫距离作为代价值时路径拐点多、波动幅度大和精确度低的现象,还解决了使用曼哈顿距离作为代价值时路径拐点多且紧贴障碍物边缘的问题。本文采用切-曼融合式作为代价值不仅在算法规划阶段降低了计算量,提高了算法效率,并且加强了算法生成路径的精确性、安全性。

另外,为验证改进后D*算法的优越性,并且保证仿真实验结果的真实性、普遍性,避免特殊环境的影响,传统D*算法、改进后的D*算法以及蚁群算法将在同一三维环境下、同一台计算机上分别进行多组不同目标点的仿真实验。实验起始点固定为(5,5,10),而在选取目标点时,应该重视环境因素对算法效率的影响。为了达到更好的效果,选择跨越整个地图的目标点和地图的不同部位,包括前、中、后段位置。作为具体示例,考虑使用坐标(83,90,45)、(45,65,35)和(86,65,45)分别代表地图上的这些位置。这3组仿真实验结果对比如图8～10所示。

(a) 传统D*算法规划的无障碍路径

(a) 传统D*算法规划的无障碍路径

(a) 传统D*算法规划的无障碍路径

从图8～10可以看出,传统D*算法的主要缺陷体现在以下几点,即:具有较高的转弯频率,且转弯路径总是紧贴障碍物边缘,不具备较高的安全性。如图9(b)所示,对于改进后D*算法生成的路径进行优化处理,上述问题有了明显改进,路径转弯频率显著降低,路径安全性得到提高。对比蚁群算法容易陷入局部最优,所得路径拐点数过多、复杂性高的问题,改进后D*算法减少了冗余拐点,路径更加简单。同时,观察改进后D*算法得出的图像结果,优化路径中拐点的转角均符合无人机动力学模型的假设,符合无人机飞行任务要求。

改进后D*算法在三维实验环境中的表现比传统D*算法更加高效。这是因为采用了变步长的方法扩展节点,并且使用切-曼融合式作为代价值,从而明显降低了算法规划阶段的计算量。此外,将生成路径投影到二维平面上进行了优化处理,减少了路径转弯频率、缩短了路径长度并降低了路径复杂性。值得注意的是,在算法总规划时间中,仅有0.12%被用于优化路径的计算判断,所以不会抵消其他优化带来的好处。

相比于使用蚁群算法的方案,改进后D*算法在规划时间和路径复杂度方面具有显著优势。更重要的是,改进后D*算法克服了传统算法转弯次数太多的缺陷,提高了无人机的飞行安全性,当路径没有过多转向的要求时,可以有效地保护发动机。在复杂的地图环境或更长的任务距离下,改进后D*算法优越性更加明显,能够更好地满足无人机飞行任务的需求,提升整体的飞行效率。

4 结 语

本文针对无人机使用传统D*算法进行三维路径规划过程中,存在效率低、拐点多,路径复杂等问题,提出一种改进D*算法。首先在扩展节点时,采用变步长的方式,根据当前节点与目标节点的远近,选择不同的步长,这样可以提高D*算法在规划阶段搜索空间的效率;同时在代价函数方面,算法利用切-曼融合式代替传统欧式距离作为代价值,在保证路径精确性的前提下使得算法计算量进一步减少,D*算法效率低下的问题得到有效解决;最后对算法所得路径进行优化处理,保存关键节点,删除冗余、不必要的路径点,优化后的路径更符合无人机飞行任务的要求,无人机的飞行效率显著提高。