基于FLAC 3D数值模拟的抗滑桩土拱效应研究

张济斌，侯付闯

(1.山西省交通环境保护中心站(有限公司)，山西 太原 030032；2.陕西中凯恒瑞工程项目管理有限公司，陕西 西安 710000)

0 引言

滑坡是全球范围内广泛发育的一种地质灾害。由于规模大、分布广泛和危害性大的特点，容易造成较大的社会影响。通常实际滑坡治理方法种类较多，如抗滑桩、截排水措施、削方减载、锚索以及格构等。其中抗滑桩方案由于布置灵活和治理效果好的原因，被广泛应用于各类滑坡的治理工程中。研究发现，抗滑桩的受力特性是极为复杂的，桩通过锚入/嵌入稳定滑床一定深度，通过桩的抗弯和桩侧摩擦阻力形成土拱共同抵抗滑坡推力。

边坡治理工程中，大多数的抗滑桩设计均无法考虑桩的土拱效应，在一定程度上造成了材料浪费。针对桩的土拱效应，秦浩锋[1]基于离心机试验和数值模拟研究了桩间净间距对不同截面抗滑桩土拱效应。结果表明，矩形桩的土拱效应比圆形桩更明显，且圆形桩的土拱极限承载力是矩形桩的73%～84%。王国田和罗雪贵[2]基于理论分析和数值模拟研究了滑坡-抗滑桩土拱效应。研究表明，端承桩的土拱效应主要体现为小主应力拱，其土拱形态为M形，土拱效应承担的荷载与土拱厚度和分布范围呈正比。韩同春[3]基于YADE离散元软件研究了的抗滑桩土拱效应。结果表明，土体深层的土拱效应比浅层更为明显，土颗粒的分布对桩后土拱效应影响极为显著。申龙[4]基于FLAC3D数值模拟研究了桩型双排抗滑桩对桩后土拱效应的影响。结果表明，矩型抗滑桩比圆型抗滑桩的遮拦效果更好，但圆形桩的受力更加均衡。向先超等[5]基于颗粒流数值模拟研究了抗滑桩土拱效应。结果表明，拱的极限承载力随桩间距与桩宽比例增大而减小，随桩土之间的相对速度的增大而增大。付厚利等[6]依托某抗滑桩治理工程，系统分析了某边坡抗滑桩的土拱效应及影响因素。结果表明，土拱效应随土体内摩擦角的增大而增大，随直径的增大而减弱，实际抗滑桩设计时要综合考虑土拱效应和地基参数等因素。

本文采用数值模拟，建立FLAC3D数值计算模型，系统的研究了抗滑桩桩后土拱的形成机理及影响因素，为滑坡治理中的抗滑桩优化设计提供工程参考。

1 抗滑桩的受力机制

抗滑桩与桩土的相互作用是典型的三维问题，在分析过程中考虑桩土的变形协调，忽略桩的位移，可简化计算过程，机损结果的相对误差也在可控范围之内。因此分析中可简化为二维问题。具体简化形式如图1所示。分析时取一定厚度的土层作为研究对象，假定土的位移沿水平方向，桩的水平位移为0。

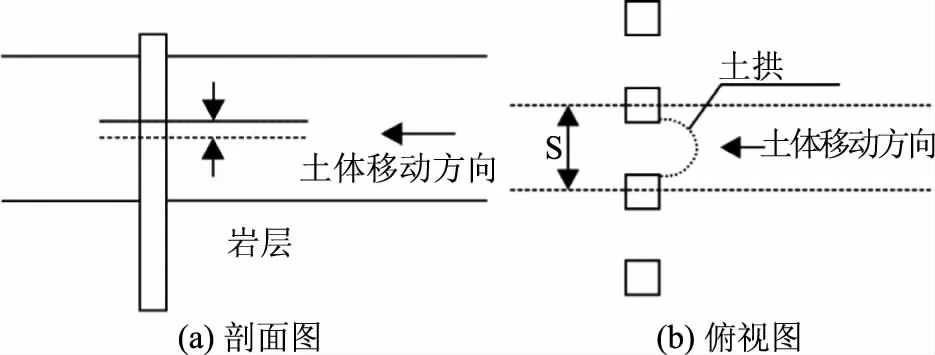
图1 抗滑桩土拱效应问题简化

抗滑桩桩后土拱形成主要是由于桩土之间的土颗粒产生不均位移，进一步导致土颗粒被压密实，形成一定范围的“土拱”。抗滑桩土拱受力分析如图2所示。其中P为抗滑桩所受的滑坡推力。P1和P2为微单元的滑坡推力和抵抗力。q1和q2为桩的侧向压力，f1和f2为桩受的剪应力。其中滑坡推力可由传递系数法确定，由于受到众多因素的影响，其他参数确定比较困难。为了获得这些参数本文采用数值模拟进行计算，分析土拱形成条件及形成过程[7-8]。

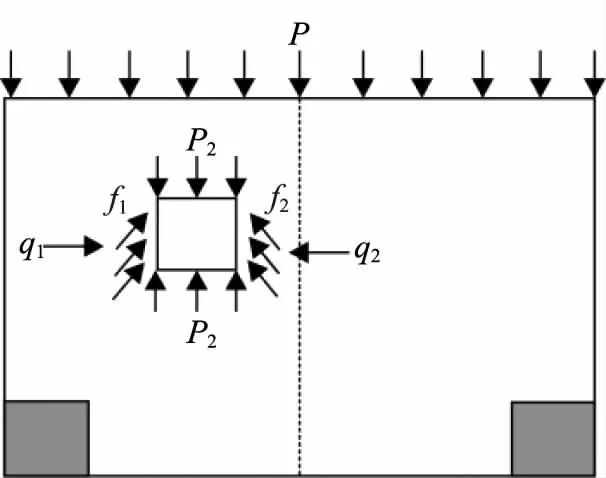
图2 抗滑桩土拱形成机理

2 数值模型与计算参数

建立典型的桩土数值计算模型如图3所示。模型高度为24m，宽度为12m，桩的宽高比为2∶3，桩间距为4m。模型的边界条件为对称边界，约束模型左右的水平位移，底部约束水平和竖向位移。网格采用4节点平面单元模型。假定滑坡推力为为3320kN/m。模型所采用的的土体和桩的物理力学参数见表1。土体采用摩尔库伦本构模型，桩采用线弹性模型。

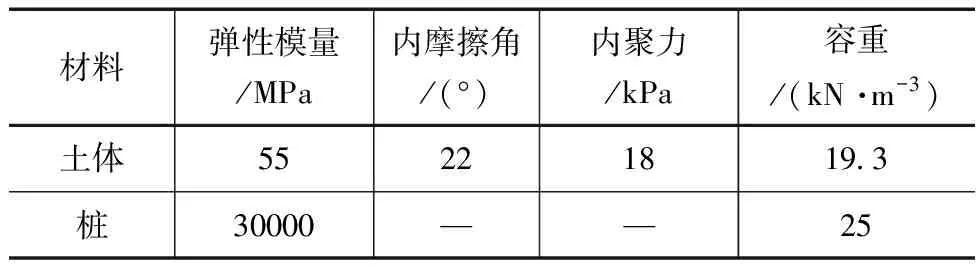
表1 材料物理力学参数取值

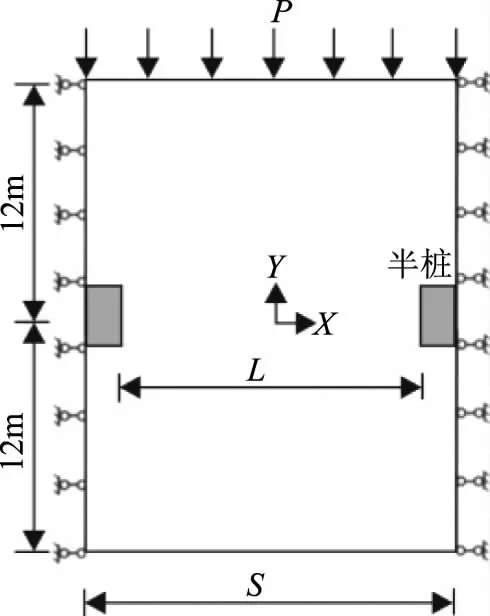
图3 数值计算模型

3 结果与分析

3.1 位移变化规律

不同滑坡推力下桩在y方向的位移如图4所示。结果表明，当滑坡推力小于3320kN/m时，桩后的位移量比较小，证明此时无土拱形成，当滑坡推力增大至1290kN/m时，土体开始发生不均匀变形。此时，土体的土拱开始形成并发挥作用。当滑坡推力进一步增大至3320kN/m时，位移迅速增大，土拱效应明显增大。根据图4，可将桩后土拱的形成分为4个阶段：①桩土相对位移较小，且土体位移有增大趋势，此时没有形成土拱；②随着位移增大，抗滑桩开始发挥作用，当土体位移达到极值时，土拱效应最明显；③随着荷载进一步增大，土拱效应减弱；④土拱效应完全消失，此时摩擦阻力是抗滑力的主要组成部分。

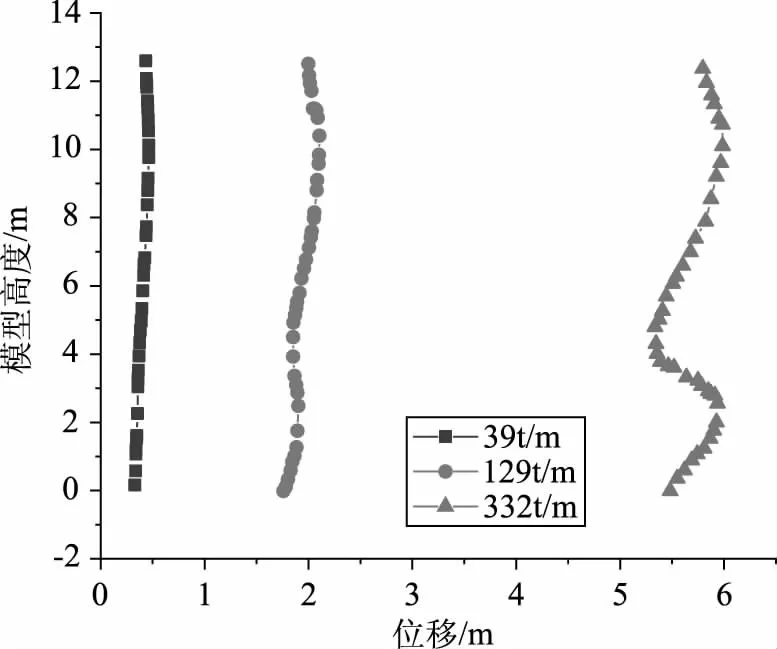
图4 滑坡推力对桩的位移影响

3.2 桩间距对土拱效应的影响

为了研究桩间距对土拱效应的影响。本文计算了在其他条件相同的情况下，不同桩间距对土拱效应的影响如图5所示。结果表明，当桩间距小于12m时，桩的位移随桩间距的减小而减小，桩土没有形成土拱。此时，桩土摩擦力是主要的承载力提供部分。当桩间距减小到8m时，土拱效应开始形成，但不明显，桩土之间的摩擦力仍占主要比例。进一步减小桩间距至6m时，桩后土拱效应明显，具体表现为桩后土体的变形趋势相同。当桩间距为4m时，土拱效应最为明显。因此实际工程设计中桩间距采用桩宽的3倍最为合理。

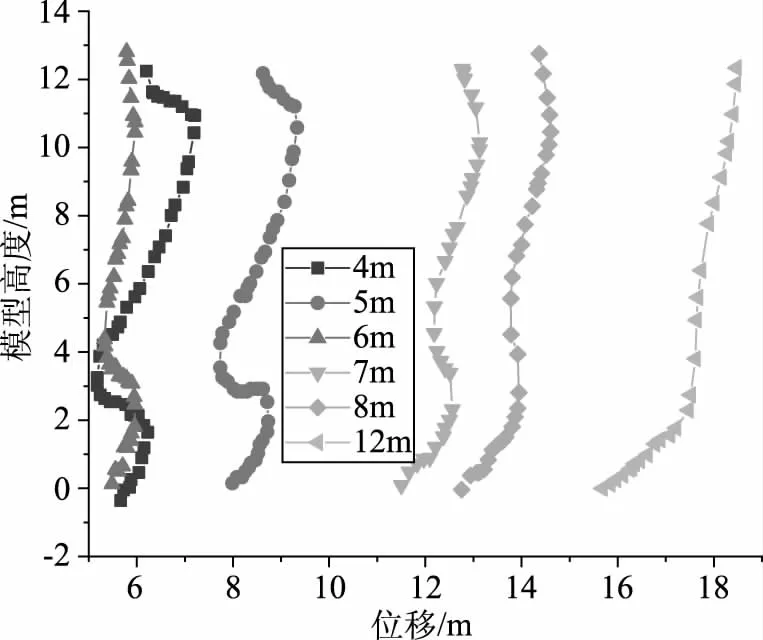
图5 桩间距对桩的位移影响

桩间距对桩土荷载分担比影响如图6所示。结果表明，桩荷载分担比随桩间距的增大而减小，而土荷载分担比随桩间距的增大而增大，在桩间距为9m时，两者的分担比相同。当桩间距为16m时，桩荷载分担比例为30%，土荷载分担比例为70%；当桩间距为4m时，桩荷载分担比例为85%，土荷载分担比例为15%。实际工程中利用该分担比可确定桩身所受滑坡推力的大小[9]。

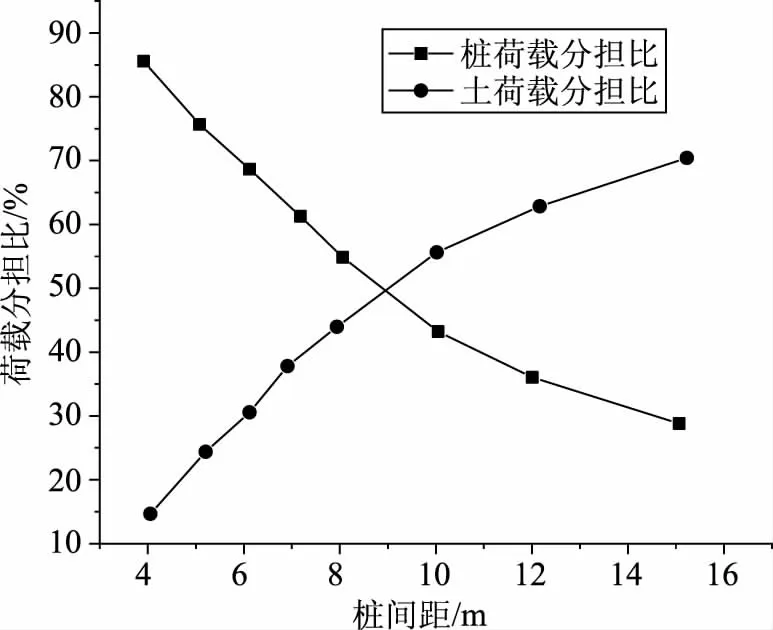
图6 桩间距对桩土荷载分担比影响

3.3 内摩擦角对土拱效应的影响

既有研究表明，土拱效应不仅受桩间距的影响，还受到内摩擦角和内聚力的影响。不同内摩擦角对桩土荷载分担比的影响如图7所示。其中固定桩间距为6m，滑坡推力为33200kN/m。结果表明，当内聚力保持不变时，桩荷载的分担比随内摩擦角的增大而增大，证明增大内摩擦角可以有效的增大土拱效应。当内摩擦角为10°，内聚力分别为4、8、12kPa时，对应的桩荷载分担比例分别为52%、53.6%、56%；当内摩擦角为30°，内聚力分别为4、8、12kPa时，对应的桩荷载分担比例分别为79.5%、81%、8.3%。因此，当内聚力较小时，土拱效应更为明显，即更多的荷载可以转移到桩上。

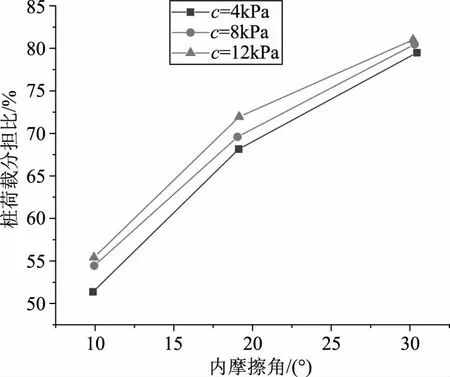
图7 土体内摩擦角对土拱效应的影响

3.4 内聚力对土拱效应的影响

如图8所示，其中固定桩间距为6m，滑坡推力为33200kN/m。结果表明，当内摩擦角保持不变时，桩荷载的分担比随内聚力的增大基本保持不变，证明增大内聚力对增大土拱效应不明显。当内聚力为4kPa，内聚力分别为10°、20°、30°时，对应的桩荷载分担比例分别为51%、68%、80%；当内聚力为12kPa，内聚力分别为10°、20°、30°时，对应的桩荷载分担比例分别为53%、70%、80%。因此，内摩擦角比粘聚力对土拱效应的影响更显著。

4 结论

本文采用FLAC3D数值计算软件研究了抗滑桩桩后土拱效应的形成机理和影响因素。结果显示当桩间距小于12m时，桩的位移随桩间距的减小而减小，桩土没有形成土拱，桩土摩擦力是主要的承载力提供部分；当桩间距为4m时，土拱效应最为明显。工程设计中，桩间距采用桩宽的3倍最为合理；当内聚力保持不变时，桩荷载的分担比随内摩擦角的增大而增大，增大内摩擦角可以有效的增大土拱效应；当内聚力4kPa，内摩擦角由10°增大至30°时，对应的桩荷载分担比例由50%提高至80%。内聚力对土拱效应的影响不显著。本文在分析过程中简化计算过程，忽略桩的位移，与实际情况可能存在偏差，需要进一步分析研究。