基于逆投影的多椭圆联合快速高精度定位算法
刘传凯,雷俊雄,刘茜,孙军,苏建华,胡晓东,李东升
1.江西理工大学 电气工程与自动化学院,赣州 341000
2.北京航天飞行控制中心,北京 100190
3.航天飞行动力学技术重点实验室,北京 100190
4.中国科学院 自动化研究所,北京 100194
在工业与航天领域,靶标作为一种辅助工具,常用于工件或目标位姿的精确测量,目前使用最为广泛的靶标类型有2 种,圆形类靶标与棋盘格类靶标。因圆形目标自身具有平移、旋转和缩放不变性,易于识别与定位,所以常选用圆形作为靶标模板,在圆上添加几何要素来构成圆形靶标;棋盘格靶标一般是由大小相等交错排列的黑白两色矩形组成,具有中心对称、角点特征易于获取等优点,所以棋盘格靶标在视觉测量领域也经常作为一种辅助测量手段。为实现工件或目标的精确位姿获取,首先对靶标在图像中的位置进行精准识别与计算,然后采用PNP(Perspective-N-Point)或 者 EPNP(Efficient Perspective-N-Point)等测量算法实现目标位姿求解,然而受不确定环境和复杂光照影响,靶标点提取的准确性一直是难以完全解决的问题,也是提升目标定位精度的关键。
与棋盘格靶标通过检测梯度极值点来提取相比,圆形靶标通过检测和筛选椭圆轮廓来提取的方式具有更好的稳定性和准确度。圆形靶标提取根据基本处理单元的不同,主要采用基于Hough 变换的椭圆检测与基于弧段的椭圆检测2 类算法。Hough 变换法使用较为广泛[1],其实现思想是通过边缘提取得到像素点并通过聚类算法来实现圆形目标的检测,但受限于计算复杂度随椭圆参数维度指数增长的性质,对存储空间和计算时间耗费较大[2],因此有学者通过椭圆自身几何特性[3-4]、多对一映射[5-6]等方式来降低Hough 变换的参数空间维度从而在一定程度上改善算法性能。基于弧段的椭圆检测算法是由Kim 等[7]提出,通过对多个像素连接的短直线组合特征的检测来确定弧段特征,进一步将多个弧段特征组合来检测椭圆。与Hough变换相比,基于弧段的椭圆检测算法无需大量的内存空间、计算效率较高,但由于弧段特性与多弧段组合为同一椭圆的约束检验不多,容易出现不同弧段错误组合形成假椭圆的情况。近年 来,Lu[8]和Meng[9]等 通 过 改 变 弧 段 提 取 方法、构造邻接弧段组合矩阵等手段提升椭圆检测的准确率,但也使得弧段匹配算法复杂,降低了算法效率。
为克服椭圆检测对靶标定位的影响,期望构建基于特征的空间映射关系来测量目标位姿,减少算法复杂度、提高计算效率的同时保持测量精度。目前较为典型的位姿测量方法是PNP 及其拓展改进方法。其基本思想是通过构建图像中靶标点与实际空间中靶标真实尺寸的对应关系,实现对目标位姿的计算。根据使用特征点数的不同可以将PNP 算法分为2 种情况[10]:一是在特征点数较少时,使用固定特征点数的特定求解方法;二是在特征点数较多时,使用任意数量特征点进行求解的通用求解方法。对特定求解方法的研究主要集中于P3P(Perspective-3-Point)、P4P(Perspective-4-Point)问题上[11-12],此类方法实现原理简单且能得到闭式解,但因使用到的特征点信息较少,对噪声极其敏感,求解的相机位姿精度不高;通用求解方法利用靶标的冗余信息来提升位姿估计的精度和鲁棒性,但计算所需时间也会随着使用特征点数目的增加而增加。使用较为广泛的通用求解方法有直接线性变换法(Direct Linear Transformation,DLT)[13]、正交迭代法(Orthogonal Iteration,OI)[14]、 EPNP 算 法[15]和 直接最小 二乘法[16]等,在处理冗余点数较多情况取得良好的效果。然而在处理合作靶标冗余量较少的情况时[17],也难以避免背景噪声与干扰点仍能对位姿解算精度的影响。
针对上述问题,本文提出了基于逆投影变换的圆形合作靶标相对位姿测量算法,在提取圆形靶标轮廓离散点的基础上,无需进行椭圆检测与拟合,将圆形靶标轮廓离散点逆向投影到三维空间中形成过光心和椭圆轮廓点的多个空间射线簇,直接在三维空间中利用射线簇构建描述靶标位姿误差的残差函数,建立对多圆形靶标位姿的整体约束与联合优化求解模型,从而实现对空间目标相对位姿的低复杂度快速求解,如图1 所示。第一,该方法避免因椭圆拟合和复杂投影距离计算导致的过程误差,提高位姿计算效率和求解精度;第二,相较传统的基于透视投影成像的多特征联合像素残差计算模型,复杂度得到极大简化;最后,通过在空间中对多个圆形靶标轮廓点集的联合平差,提升算法对投影误差和错误点的抗扰能力,使得定位性能明显改善。
1 圆形靶标逆投影位姿测量
针对利用少量圆形靶标测量空间目标位姿中存在的计算过程复杂、易受噪声干扰等问题,本节设计了基于成像光束逆投影的多圆形靶标联合平差测量框架,首先利用圆形靶标轮廓点的逆投影方程构建空间射线簇,然后在空间中构建距离残差函数和目标位姿优化模型,分析模型收敛初始域并设计迭代优化算法实现位姿优化求解,具体过程详述如下。
1. 1 空间圆成像投影模型
假设世界坐标系原点为Ow,靶标坐标系原点Ot,相机坐标系原点Oc位于相机光心,靶标坐标系及相机坐标系相对于世界坐标系的变换矩阵wΤt和wΤc分别表示为
式中:wRt∈R3×3和wRc∈R3×3分别表示圆形靶标和相机的姿态变换矩阵;wXt∈R3×1和wXc∈R3×1分别表示靶标和相机的位置向量。
对于多圆形靶标上第i 个圆形目标轮廓上第j 个空间点P(i,j),其在世界坐标系和相机坐标系下的位置向量分别表示为wX(i,j)∈R3×1和cX(i,j)∈R3×1。则 空 间 点P(i,j)通 过 透 视 投 影 成 像原理投影到相机图像中对应的像素坐标u(i,j)为
式中:δM ∈R3×3和pM(i,j)∈R3×3分别表示相机的畸变参数矩阵和空间点P(i,j)到 相 机 图 像 的 透 视投影变换矩阵。
令Δu=[Δu,Δv,0]表示相机镜头畸变造成的投影点偏移;fu和fv表示相机焦距,单位为像素;u0=[u0,v0,0]T表示图像主点坐标。畸变修正后空间圆的投影像素坐标为
式中:diag( fu,fv,1)表示对角矩阵;cz(i,j)表示空间点在相机坐标系下的Z 坐标,即cz(i,j)=;n 表示法向量,有n=[0,0,1]T。
1. 2 空间圆轮廓点位姿表示形式
多圆形靶标上第i 个圆形目标轮廓上第j 个空间点P(i,j)的逆投影成像如图2 所示。其中,wXti表示第i个圆形目标圆心的世界坐标,有wXti=坐标系原点Ot的相对位置关系;wnt表示靶标法向量在世界坐标系下的表示,有wnt=wRtn;wTttXti,式中tXti表示第i个圆形目标圆心与靶标wv(i,j)表示相机指向空间点P(i,j)的单位方向向量,且方向向量穿过空间点P(i,j)在相机图像上经修正后的投影像素坐标,有
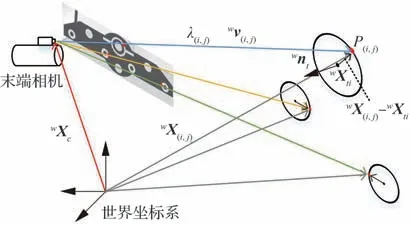
图2 空间圆轮廓点的逆投影成像示意图Fig.2 Diagram of inverse projection imaging of circular contour points
式中:cv(i,j)表示相机指向空间点P(i,j)的 单 位 方 向向量在相机坐标系的表示。
圆形目标平面任意向量与靶标坐标系法向量wnt垂直,则第i 个圆形目标圆心wXti到空间点P(i,j)的 向 量(wXc+λ(i,j)wv(i,j)-wXti)与wnt垂直,根据正交向量的内积为零,即,得到直线距离λ(i,j)为
因此,空间点P(i,j)的位姿可通过空间机械臂末端相机坐标系表示为
1. 3 位姿优化模型的构建及收敛性
设多圆形靶标第i 个圆形目标的半径为ri,利用目标圆心到空间圆形目标轮廓上任一空间点P(i,j)的距离等于半径长度,构建空间点P(i,j)的 非线性残差函数为
与前期工作[18]不同,多圆形靶标的残差函数利用多目标在二维图像平面与三维空间中的信息计算尺度一致的空间距离作为因变量,充分利用靶标的几何要素并据此提升残差函数的稳定性。
为分析残差函数在一定范围内的收敛性质,通过MATLAB 平台构建多圆离散轮廓点与相机,模拟相机位姿Ω=[x,y,z,θx,θy,θz]T分别发生(-1 m,1 m)的位置偏移与(-10°,10°)的姿态偏移时对误差函数e(i,j)造成 的影响,如图3 所 示,其中θx、θy、θz为相机的三个姿态角。

图3 误差函数随相机位姿误差的变化Fig.3 Surface of error function with changes of camera position and pose
从图3 中可以看出,当相机存在(-1 m,1 m)范围内的位置误差或(-10°,10°)范围内的姿态误差时,误差函数的形状为碗状,具有很好的收敛性,并且收敛点位于相机位姿真值附近,说明本文提出的优化模型在相机位姿单独存在较大的位置误差或姿态误差时仍能保证误差函数收敛到真值,并不会出现收敛到局部最小值、错误真值的情况。
进一步探讨相机位置与姿态同时存在误差时对误差函数产生的影响,将相机姿态同时加上1°或10°,画出相机xy、xz 位置组合在一定范围内变化时误差函数的变化情况,如图4 所示。
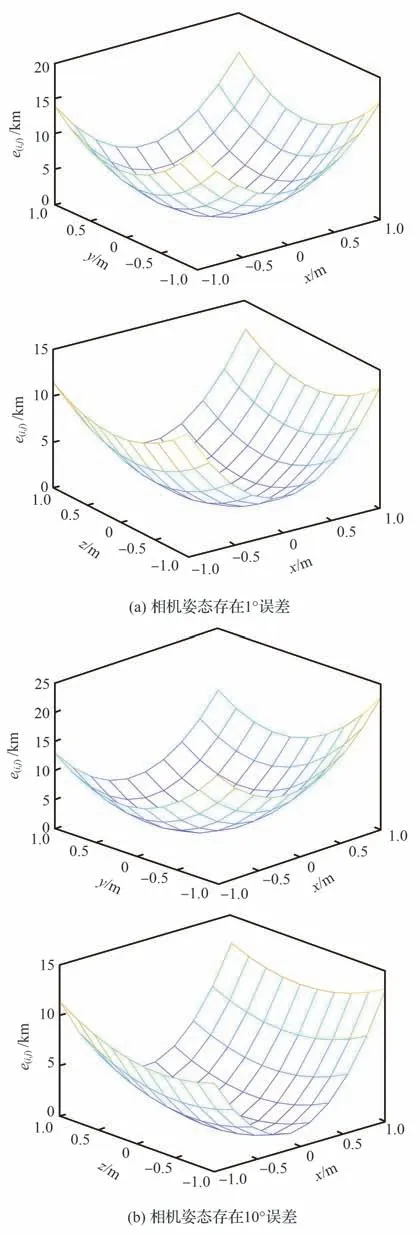
图4 相机姿态存在误差时误差函数随相机位置误差的变化Fig.4 Surface of error function with changes of camera position when camera pose error is existed
从图4 中可以看出,当相机姿态存在较小误差时,相机位置在一定范围内变化并不影响误差函数的收敛性,而当姿态误差增大时,会使得误差函数的碗状变得更加平滑,收敛性变弱,虽然仍能保持一定的收敛性,但收敛点已经发生偏移,不再收敛到相机位姿真值。
综上所述,相机位置误差对误差函数收敛性的影响较小,而姿态误差对误差函数收敛性的影响较大,会增加位置变化对误差函数造成的影响,并且使收敛性变差、收敛点发生偏移,所以在使用本文算法解算相机与目标之间的相对位姿时,应尽量保证相机姿态初值的准确。
1. 4 位姿优化模型的求解
通过对模型的收敛性分析可知位姿优化模型在一定范围内满足凸函数条件,因此可将基于多圆形靶标测量末端相机位姿问题归纳为关于上述非线性残差函数的非线性最小二乘问题,最小化空间圆圆心到轮廓点的距离与圆形半径之间的误差,即
式中:Ω=[x,y,z,θx,θy,θz]T分别表示优化过程中末端相机的位置和姿态参数;N 表示多圆形靶标中圆形目标的个数;Mi表示第i个圆形目标的轮廓点的个数。
上述典型的非线性最小二乘问题可通过Levenberg-Marquardt(L-M)法迭代求解,考虑到优化模型对相机姿态误差更加敏感,因此需要在迭代过程中增加对姿态误差的惩罚权重,以保证相机姿态收敛的准确性。L-M 法求解流程如算法1所示。其中,L-M 法第k次迭代的残差函数矩阵定义 为;第k 次的残差函数矩阵对Ω 中6个变量求偏导的雅可比矩阵定义为,即

算法1 L-M 法求解流程输入步骤1步骤2步骤3基于机械臂当前关节构型和基座位姿经正运动学结算得到末端相机初始迭代值 Ω0=[x0,y0,z0,θx0,θy0,θz0]T、常量β、σ ∈(0,1),当前迭代步数k=0、收敛阈值ε 取非常小的值,s 表示Ω 的长度,即s=6。取Ω=Ωk 计算残差函数矩阵ek(Ωk)及其雅可比矩阵Jk(Ωk)。计算gk=Jk·ek,如果norm(gk)≤ε,迭代结束并返回Ω=Ωk,否则进入步骤3。计算残差函数矩阵下降方向dk=-(JT k ·Jk+muk Es×s)-1·gk,其中muk=norm(ek)。步骤4采用Armijo 算法线性搜索合适的下降步长hk,满足ek(Ωk+β∧h·dk)≤ek(Ωk)+σβ∧hg-1 k dk 的 最 小h 值。步骤5输出更新自变量Ωk+1=Ωk+βhk dk,返回步骤2。末端相机精确位姿解Ω。
优化模型的求解中最重要的一步就是相机初始迭代值的选取,从1.3 节的收敛性分析可知,优化模型的收敛性与相机位置误差关联不大,所以当初始迭代值的姿态与相机姿态真值相差不多时,可以利用L-M 法求取末端相机的精确位姿,从中国空间技术研究院给出的数据显示[19],中国空间站机械臂的位置精度与姿态精度分别为45 mm、1°,位姿精度在优化模型的收敛域内,所以可以在相机位姿真值基础上,将相机位置在(-45 mm,45 mm)范围内偏移,姿态在(-1°,1°)范围内偏移得到的新相机位姿作为基于机械臂当前关节构型和基座位姿经正运动学结算得到末端相机初始迭代值。
2 实验验证与分析
为验证本文算法的有效性,本节首先采用MATLAB 仿真的方式对算法定位精确性和抗扰能力进行验证,然后通过虚拟仿真平台获取靶标仿真图像开展空间目标测量定位实验,通过与PNP 算法等靶标定位方法比较,验证本文算法有效性和优越性。
2. 1 仿真合成图像
此节选用空间站机械臂适配器上安装的2 类典型靶标[20-21]进行仿真实验,2类靶标如图5所示。

图5 中国空间站上所使用的2 款靶标[20-21]Fig.5 Two types of targets used on China space station[20-21]
在MATLAB 软件中开展仿真实验,首先定义靶标坐标系,靶标坐标系相对于世界坐标系的平 移向量wXt设 为[7 700 mm,-846.6 mm,-1 209.1 mm]T,靶标平面相对于世界坐标系的滚 转 角ψ、俯 仰 角γ 与 偏 航 角φ 分 别 设 为0°、-55°、90°,然 后 分 别 构 建2 组 离 散 点 序 列 组 成2 个合作靶标,2 个靶标中各圆形目标与靶标坐标系原点的相对位置tXti、圆形目标半径ri按照一定比例设置。定义Ω=[x,y,z,θx,θy,θz]T为相机在世界坐标系下的位姿参数,K 为仿真相机的内参矩阵,设置如下:
根据透视投影关系将靶标轮廓点变换到像平面上得到靶标轮廓像素坐标,相机位姿初始迭代值的选取依据1.4 节所述,将经迭代求解出的相机位姿精确解与设置的相机位姿真值Ω 作误差分析,定义相机光心位置误差为Δepose=|x-姿 态 误 差 为Δeori=|θx-,将相机的x 坐标固定在7 660 mm 不动,然后控制相机在y-z 方向从[-1 625 mm,-1 860 mm]逐渐向后移动2 m 以模拟相机在不同距离环境下对2 种靶标的识别与定位,取-200 mm 为每次测试的递增距离,对于每组测试,取100 次独立实验的位置和姿态误差均值作为实验结果,如图6和图7所示。

图6 相机在y-z 方向移动时相机位置和姿态的误差(第1 种靶标)Fig.6 Camera position and pose errors when camera moves in y-z direction(the first target)
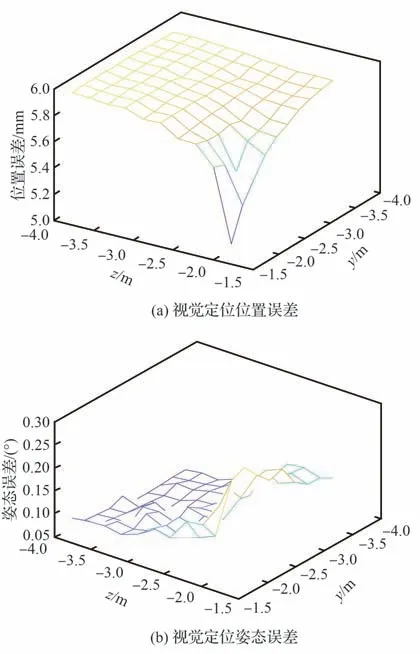
图7 相机在y-z 方向移动时相机位置和姿态的误差(第2 种靶标)Fig.7 Camera position and pose errors when camera moves in y-z direction(the second target)
从图6 和图7 中可知,当相机与靶标的距离逐渐增大时,利用本文提出算法解算出的相机位置误差也逐渐增大,但姿态误差却逐渐减小,结合残差函数收敛性对此原因进行分析,这是因为远距离时,姿态存在较小的误差会引起更大的位置误差,所以迭代过程中为保证位置的精度,姿态误差会略微减小,并且y-z 方向的位置误差增长近似对称,是因为相机光轴方向指向y-z 之间,当相机在y-z 方向移动时可以近似为在光轴方向移动,即在两方向产生的误差相近。另外通过实验比对分析可知,因第1 种靶标使用的圆个数(4 个)比第2 种靶标(9 个)少,所以第1 种靶标的位置误差较大,但针对上述2 种靶标,当在相机光轴方向且相机和靶标相距2 m 以内时,相机位置与姿态的平均误差分别<6 mm、0.4°,具有较高的测量精度。
为验证本文算法对强背景噪声等干扰的抵抗能力,下面仿真实验中引入高斯白噪声,与PNP 算法比对定位精度情况。首先构造第1种合作靶标空间离散点在相机图像上经修正后的投影像素坐标归一化前分别加入标准差为1~5 的高斯白噪声,用于模拟不同干扰情况下对目标透视投影过程产生的影响,然后将带有噪声的像素坐标代入本文算法与椭圆拟合+EPNP 算法分别求解相机位姿,其中椭圆拟合部分是用拟合靶标离散圆环点来代替,EPNP 算法则是通过第1种靶标的4 个圆形目标的拟合圆心进行计算。为分析不同方法的位姿测量误差,每种噪声环境下进行100 次独立的实验,求取100 次的平均位置误差平均姿态误差,其中[ x,y,z,θx,θy,θz]T=[7 660 mm,-1 825 mm ,-1 860 mm,0°,-55°,90°]T实验结果如图8所示。
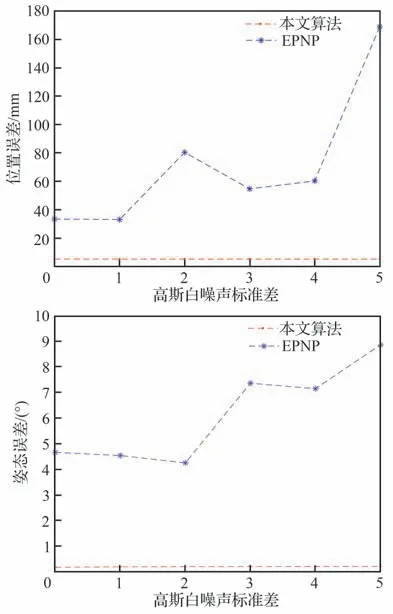
图8 本文算法与EPNP 算法在不同噪声环境下的位置误差与姿态误差比较(第1 种靶标)Fig.8 Comparison of position error and pose error between proposed algorithm and EPNP algorithm in different noise environments (the first target)
从图8 中可以看出,在计算四圆靶标与相机的相对位姿时,本文算法的抗干扰性要远远强于EPNP 算法。同样地,针对第2 种靶标,在相同噪声环境下使用本文算法以及椭圆拟合+PNP 算法分别对相机位姿进行求解,因第2 种靶标的圆数量更多,所以PNP 算法分别使用基于最小二乘优化重投影误差的Iterative 迭代法与EPNP 算法。在解算相机位姿时,因EPNP 算法可以使用任意数量的特征点来估计位姿,所以本文算法和EPNP 算法使用9 个圆形目标,而Iterative 迭代法仅使用共面的4 个特征点,实验结果如图9所示。
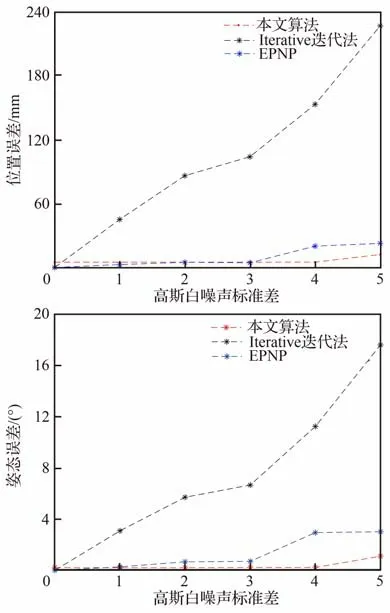
图9 本文算法与2 种PNP 算法在不同噪声环境下的位置误差与姿态误差比较(第2种靶标)Fig.9 Comparison of position error and pose error between proposed algorithm and two types of PNP algorithms in different noise environments (the second target)
从图9 中可以看出,当空间点透视投影到图像平面不存在噪声或存在很小的噪声干扰时,本文算法与EPNP 算法解算的相机位姿均具有较高精度,而Iterative 迭代法表现不佳;随着噪声的不断增大,Iterative 迭代法的位置误差与姿态误差急剧上升,在标准差=5 时的位置与姿态误差分别达到230 mm 与17°,抗干扰性最差;使用更多的冗余信息的EPNP 法抗干扰性优于Iterative迭代法,但是当加入的噪声标准差≥3 时,求取的位姿误差也在大幅增加;与2 种PNP 算法相比,本文算法在弱噪声环境下有着较高精度,在噪声逐步增强的情况下误差曲线平稳上升,在标准差=5 时3 个方向的位置与姿态误差分别<15 mm 与1.8°,即单方向位置误差≤5 mm,单方向姿态误差≤0.6°,具有极强的抗干扰性。
结合图8 与图9 分析,EPNP 算法在使用不同数量的特征点时,计算精度有所不同,其中对于特征点数目更多的第2 靶标,EPNP 算法的抗干扰性得到一定提升,而本文算法在2 种靶标下计算得到的位姿均具有较高的精度。根据以上实验可以得出结论,在无噪声或噪声较小的情况下,使用四圆靶标、九圆靶标计算得出的位姿精度相当,且均略高于同实验条件下的PNP 算法,而在噪声较大的环境下,使用四圆靶标计算出的位姿精度最高、抗扰性最强,九圆靶标的精度稍差,但也强于PNP 算法。
2. 2 虚拟仿真平台
为更好地验证本文算法的有效性与精度,搭建了虚拟仿真平台,构建与空间站核心舱机械臂适配器上相似的合作靶标,靶标及编号如图10 所示,其中1 号圆的白色外圈半径最大,中间白色圆形外圈半径最小,其他2~8 号的白色外圈半径一致,合作靶标安装在适配器左上角,且靶标上的每个圆形目标与适配器之间的相对位姿关系已知,如表1 所示。
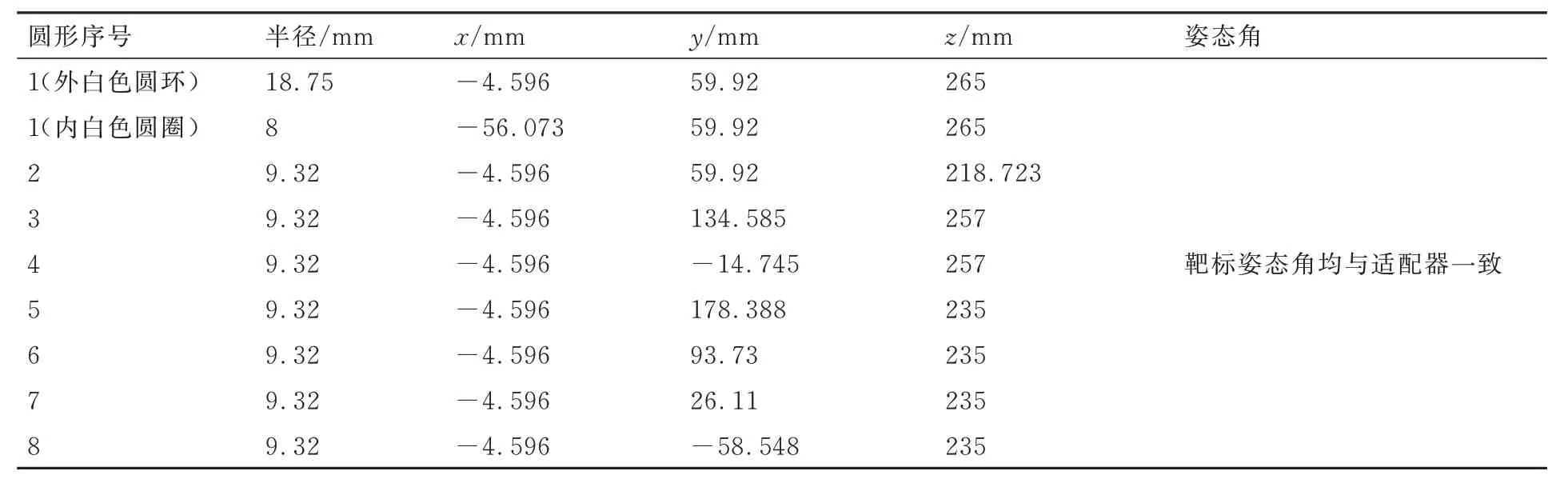
表1 靶标各圆形目标尺寸及与适配器之间的相对位姿关系Table 1 Dimensions of each circular target and relative positional relationship between target and adapter
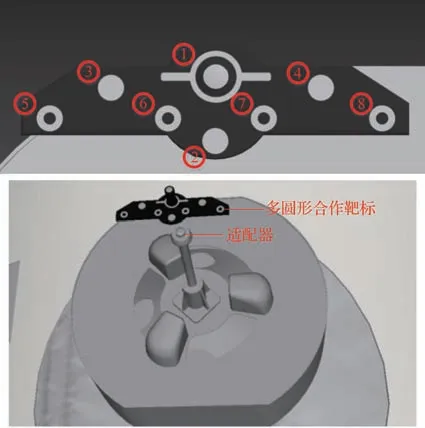
图10 多圆形合作靶标与适配器样式Fig.10 Type of multi-circular cooperative target and adapter
然后创建内参fu和fv已知的相机仿真模型,为模拟真实情况下相机对合作靶标的拍摄情况,利用相机从9 个不同方位由远及近地对靶标区域进行拍摄,每个方向获取2 张距离不一的合作靶标图像总计18 张图像,如图11 所示。

图11 从不同方位、不同距离获取的合作靶标图像Fig.11 Images of cooperative targets acquired from different orientations and distances
为精确获取图像中靶标的所在区域,减少合作靶标检测的无效干扰,使用Halcon 形状匹配算法[22]来识别图像中的合作靶标并对其最小外接矩形进行截取,如图12 所示。Halcon 形状匹配的原理是结合合作靶标的边缘特征与灰度信息来创建模板,然后在待匹配图像的图像金字塔中逐层搜索模板图像至最底层或得到确定的匹配结果为止。

图12 多圆形靶标区域提取结果Fig.12 Multi-circular target area extraction results
在得到裁剪过的靶标区域后,使用Canny 边缘检测算法来提取合作靶标上圆形目标的轮廓像素点u(i,j)(i=1,2,…,8)并通过人工分组的方式将所有检测到的轮廓点分别归入到9 个圆形目标,在靶标被遮挡或在视角范围外时,提取剩余圆形目标的轮廓像素。在仿真平台中,将适配器设为靶标坐标系原点,其在世界坐标系下的位姿设置与 2.1 节仿真实验一致,即wXt=[7 700 mm,-846.6 mm,-1 209.1 mm ]T,适配器相对于世界坐标系旋转的三角度为[ψ,γ,φ]T=[0°,-55°,90°]T。各圆环圆心的世界坐标wXti由表2 与wTt计算可得。
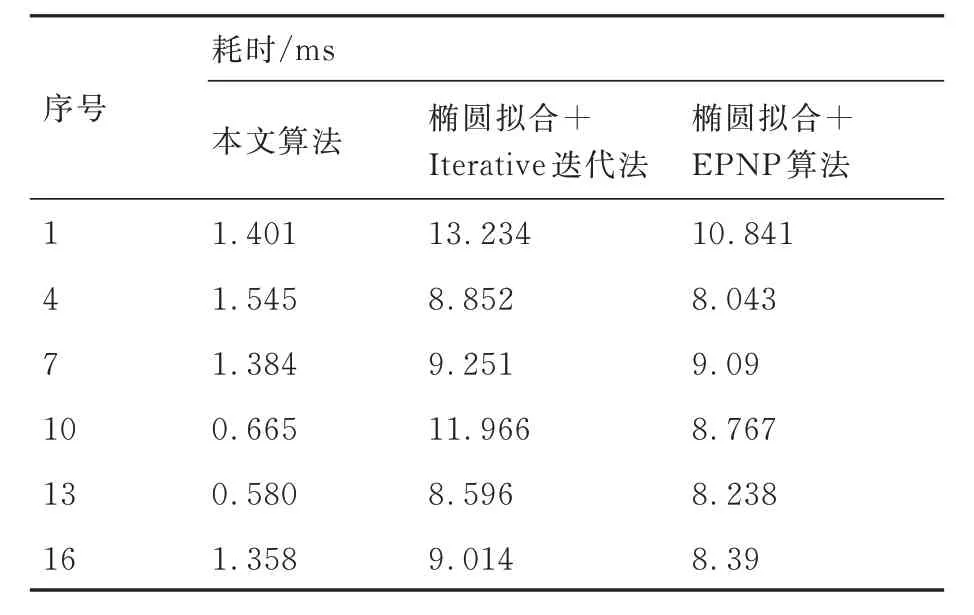
表2 视觉定位部分实验中本算法与2 类PNP 算法的耗时比较Table 2 Comparison of time consumption between our algorithm and two types of PNP algorithms in part of visual localization experiment
图13 为针对上述18 张合作靶标图像使用本文算法解算的世界坐标系下的相机位姿与真值之间的误差。其中位置误差由x 方向误差Δx、y 方向误差Δy 与z 方向误差Δz 表示,姿态误差由滚转角误差Δθx、俯仰角误差Δθy与偏航角误差Δθz表示。
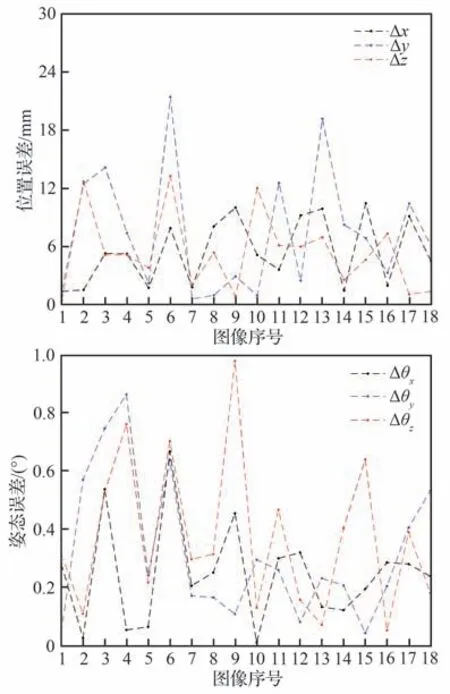
图13 利用本文提出算法计算的相机位姿误差Fig.13 Camera position error and pose error calculated using our algorithm
从仿真实验结果可知,本文算法解算的不同距离相机位姿均具有较高精度,其中单方向的位置误差≤25 mm,姿态误差≤1°,因仿真平台中拍摄的图像存在一定的图像噪声与轮廓像素提取误差,即使是使用相机真值代入到优化模型中计算出的残差也不为0,所以将迭代收敛阈值ε 设为10 mm,此情况下则会导致相机距离目标更远情况下的定位精度可能略高于相机距离目标更近情况下的精度。
为验证改进算法在精度与性能上的优势,同样使用椭圆拟合+PNP 算法对这18 组图像的相机位姿进行解算并与本文算法进行比较,其中椭圆拟合使用的是最小二乘法来对离散轮廓点进行拟合,PNP 方法使用的是Iterative 迭代法与EPNP 算法。实验采用QT 5.9.0 编译器,边缘检测、椭圆拟合、2 种PNP 算法与本文算法均用C++语言编程,其中Iterative 迭代法与EPNP 算法采用OpenCV 3.2.0 版本的内置函数,本文算法基于Eigen 矩阵运算库实现,程序运行计算机配置为Intel(R) Core(TM) i7-5500U CPU @ 2.40 GHz,8G RAM。
图14 为针对上述18 张合作靶标图像数据使用本算法、Iterative 迭代法与EPNP 算法分别解算的世界坐标系下的相机位姿与相机位姿真值之间的误差。由于存在靶标圆环被遮挡、靶标位于相机视角外等情况,所以Iterative 迭代法使用的是经边缘检测算法成功提取到的前4 个共面圆环轮廓点拟合圆心,EPNP 算法使用的是经边缘检测算法成功提取到的所有圆环轮廓点拟合圆心。

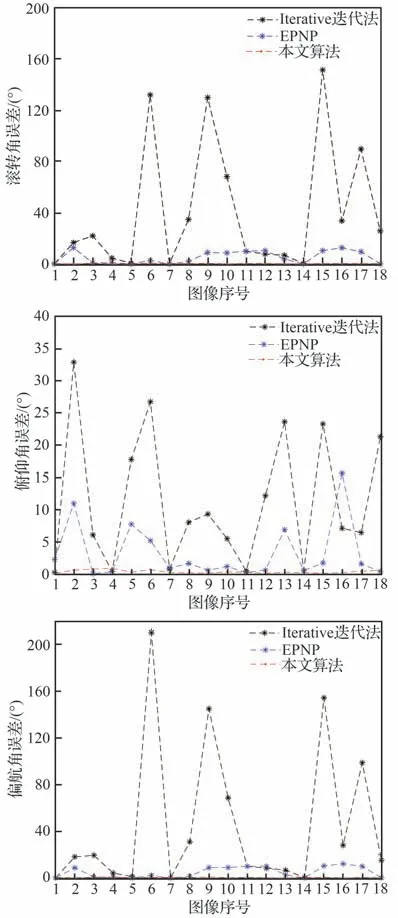
图14 本文算法与2 种PNP 算法的相机位姿误差比较Fig.14 Comparison of position error and pose error between proposed algorithm and two types of PNP algorithms
从图14 中可以看出,本文算法在相机从不同视角、不同距离拍摄合作靶标的情况下均取得较高精度,也比相同条件下的PNP 算法表现更佳,PNP 算法在靶标距离相机较近且相对相机角度偏移不大的情况下才可能取得较高的精度,并且因本算法使用更多冗余点信息,在PNP 算法表现不佳的情况仍能求取高精度的相机位姿,普适性更强。位置误差中,x 方向的位置平均误差比其他2 个方向的平均误差小,这是因为相机光轴指向世界坐标系y、z 轴之间,而相机在光轴方向移动时会直接造成目标与相机之间深度的变化,误差会更大。与2.1 节MATLAB 仿真合成图像的第2 种靶标实验相比,虚拟仿真平台下各算法的精度都有降低,这是因为数字虚拟平台中需要考虑的误差因素更多,例如图像噪声、相机标定误差、边缘提取与椭圆拟合的误差等,与实际任务场景更为接近。
进一步对本文算法与PNP 算法的时效性进行比较。图15 为上述18 次实验中本算法与椭圆拟合+两种PNP 算法的耗时比较。
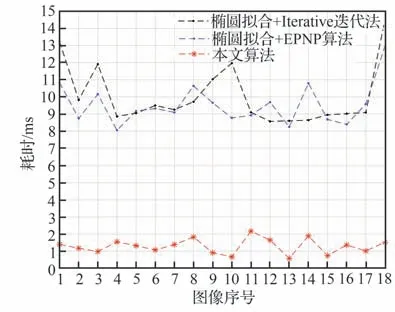
图15 18 次实验中本文算法与椭圆拟合+2 种PNP 算法的耗时比较Fig.15 Comparison of time consumption between proposed algorithm and ellipse fitting + two types of PNP algorithms in 18 experiments
由于Iterative 迭代法与EPNP 算法所需拟合的圆心数量不同,所以椭圆拟合步骤的耗时也不相同,图15 中的椭圆拟合+2 类PNP 算法耗时是由Iterative 迭代法或EPNP 算法对应的椭圆拟合耗时再加上其本身耗时得到。为更直观地给出视觉定位流程中本文算法与椭圆拟合+PNP 算法定位策略时间的差异情况,每隔3 组抽取1 组实验数据,即第1、4、7、10、13、16 次实验数据的比对如表2 所示。
从图15 和表2 中可以看出,椭圆拟合+Iterative 迭代法的耗时与椭圆拟合+EPNP 算法的耗时相当,而本文算法耗时远小于椭圆拟合+2 种PNP 算法的耗时。此次实验重点比较靶标定位最简步骤的所需时间,假定靶标已经完成识别提取,所以在对2 种PNP 算法计算位姿的过程中采用简单的轮廓拟合+定位的方式。而在实际应用中,PNP 算法使用前为了提取更加准确的靶标椭圆轮廓,往往采用更为复杂的椭圆检测算法,时间耗费会更大,因此本文算法较2种PNP 算法的时效性能方面有显著提升。该算法在中国空间站机械臂抓捕适配器的地面监视与实时测量任务中得到应用,在精度、稳定性和时效性方面表现良好。
3 结 论
本文针对目前基于合作靶标的视觉定位中存在的靶标点提取运算复杂、易受干扰而导致时效性、稳定性和精确性不高等问题,设计了基于多圆形合作靶标的视觉定位方法,将提取到的圆形靶标轮廓离散点逆投影至三维空间中形成多个空间射线簇,在空间中构建残差函数实现目标位姿的精确求解。通过2 类实验验证了提出算法的有效性:
1)仿真合成图像实验。在MATLAB 仿真平台上设计2 种靶标测试本文算法在不同距离、不同噪声下的定位性能,取得较PNP 算法更好的定位精度和抗干扰性。
2)虚拟仿真平台实验。在虚拟仿真平台中模拟空间机械臂在轨抓捕目标适配器的过程,利用相机从不同方位对合作靶标进行提取与定位,对不同视角拍摄的靶标图像使用本文算法与PNP 算法对相机位姿进行解算,本文算法计算得到的相机位置与姿态均取得了较高精度,满足中国空间站机械臂末端的视觉定位精度要求与实时性要求,验证了本文算法的精确性及时效性。
本文算法在空间站机械臂抓捕适配器的地面监视过程中得到应用,其精度、稳定性和时效性均取得良好的效果。该方法可应用于星舰对接环抓捕、机械臂对光学舱抓捕等多类合作与非合作任务场景中,实现对单个或多个圆形目标的快速稳定精确视觉测量,为中国航天任务的相对视觉测量能力的提升提供有力的理论与技术支撑。
致 谢
论文在北京航天飞行控制中心空间遥操作团队的通力协助下得以顺利完成,在此深表感谢。

