物理化学模型对流场电磁散射特性的影响

陈伟芳，孙精华，田得阳，陈烨斯

1.浙江大学 航空航天学院，杭州 310027

2.中国运载火箭技术研究院 空间物理重点实验室，北京 100076

3.中国空气动力研究与发展中心 超高速空气动力研究所，绵阳 621000

高超声速飞行器在飞行过程中产生的等离子体鞘套对入射电磁波的反射、折射与吸收效应会显著改变飞行器的目标电磁散射特性，导致等离子体包裹的高超声速流场对雷达入射波呈现出的频率响应是动态起伏的，其反射波与散射波具有与飞行器本体目标不同的雷达特征信息，给雷达系统进行飞行器识别、探测以及实时定位带来了障碍［1-2］，因此计算和分析不同情况下高超声速飞行器等离子体流场的电磁散射特性十分重要。

国外的研究起步较早，Rusch 和Yeh［3］采用解析的方法分析了一种无限长非均匀等离子体圆柱的电磁散射特性，并归纳了外加磁场、等离子体鞘套厚度等对散射波的影响。Swift 等［4］研究了任意入射角度的电磁波在非均匀等离子体中的传播问题，得到了散射特性的典型解。Laroussi 和Roth［5］在此基础上分析了任意入射角度的电磁波在等离子体中的散射，讨论了衰减系数、相位系数等随等离子体密度和碰撞频率的变化规律。20 世纪90 年代后，学者借助数值仿真对等离子体鞘套和电磁波的相互作用有了深入的研究。Usui 等［6］研究了包覆飞行器的等离子体鞘套的雷达散射截面积（Radar Cross-Section， RCS）空间分布特性，并采用粒子网格 （Particle in Cell，PIC）方法研 究了外磁 场 的影响。Luebbers 等［7］运用时域有限差分（Finite-Difference Time-Domain， FDTD）方法研究时变等离子体的三维散射特性。Sotnikov 等［8］对飞行器湍流引起的电磁散射特性进行了分析。Schuler 等［9］利用射线追踪方法对高超声速飞行器目标的电磁散射特性做了相关研究。

中国在这方面起步较晚，于哲峰等［10-12］首次系统地对升力体外形临近空间飞行器雷达散射截面特性开展了研究，主要研究了本体及绕流RCS特性，亚密湍流尾迹RCS 特性和层流尾迹的RCS特性等内容。马平［13-15］和吴明兴［16］等利用弹道靶实验对球模型和高超声速飞行器模型本体及绕流RCS 特性进行了分析和研究。聂亮等［17］采用空气七组元化学反应方程，数值模拟了高超声速等离子体流场，利用分段线性电流密度递归卷积时域有限差分（Piecewise Linear JE Recursive Convolution Finite-Difference Time-Domain，PLJERC-FDTD）方法计算了P 波段和L 波段后向雷达散射截面。莫锦军［18］针对低频、宽带雷达在反隐身中的可能应用，从理论预估和实验测量方面研究隐身目标的低频、宽带电磁散射特性。周超等［19］利用FEKO 软件和物理光学方法研究了等离子体对电磁波的衰减机理，并在此基础上分析了再入段弹头包覆等离子体对RCS 的影响。梁世昌等［20］采用数值仿真和实验相结合的方法，用FDTD 方法对等离子体鞘套包覆的目标组合体的电磁散射特性进行了数值仿真，将仿真的RCS 与气动物理靶实验得到的实验数据对比，验证了FDTD 方法计算等离子体电磁散射的有效性。孟贵平［21］对等离子体鞘套包覆的再入体电磁散射特性进行了深入的研究和分析。赵泽康［22］研究了高超声速目标在湍流等离子体中的电磁散射特性，分析不同入射条件以及飞行场景对电磁散射结果的影响。牛戈钊等［23］利用电流密度卷积时域有限差分法模拟了线极化平面电磁波与高超声速飞行器之间的相互作用过程，分析了等离子体鞘套包覆高超声速目标的双站极化散射特性。

目前的研究尚未充分考虑不同物理化学模型对等离子体流场电磁散射特性的影响，本文针对高超声速类HTV-2 飞行器外形，基于考虑不同化学反应动力学模型和湍流模型计算得到的高超声速等离子体流场数据，采用三维时变等离子体PLJERC-FDTD 数值计算方法，探索不同物理化学模型对高超声速飞行器等离子体流场电磁散射特性的影响，研究等离子体流场与电磁波相互作用的机理性问题。

1 理论算法

1. 1 时域有限差分方法

时域有限差分方法（FDTD）是求解Maxwell微分方程的直接时域方法，经过多年来的发展已经成为一种成熟的数值方法，在电磁散射、电磁兼容、微波电路、非线性器件、天线设计、遥感、光学技术等领域都得到了迅速发展和广泛的应用［24-25］。本文主要采用分段线性电流密度递归卷积时域有限差分（PLJERC-FDTD）方法进行电磁散射特性的研究。

在非磁化、冷等离子体中，Maxwell 方程组及相关联立方程可表示为［26］

式中：E 为电场强度；H 为磁场强度；J 为极化电流密度；ε0和μ0分别为真空中的介电常数和磁导率；ne为电子数密度；ue为电子平均速度；v 为等离子体碰撞频率；e 和me分别为电子的电量和质量。

在时间步nΔt，电流密度J 分量表达式为

式中：i=x，y，z，且有

由式（5）可得

式中：Ψni为卷积项，其表达式为

递归卷积项Ψni可写成迭代式：

电场迭代方程和磁场迭代方程分别为

1. 2 激励源

用FDTD 方法处理电磁场问题时，激励源有很多类型，从时间分布来看有时谐源和脉冲源，从空间分布来看有面源、线源、点源等。本文选用的是高斯脉冲：

式中：Ei为入射波电场强度的大小；w 为常数，决定高斯脉冲的宽度。脉冲峰值出现在t=t0时刻，高斯脉冲及频谱如图1 所示。

图1 高斯脉冲及频谱Fig.1 Gaussian pulse and its spectrum

1. 3 算法有效性验证

根据文献［27］，采用PLJERC-FDTD 算法计算半径r=1.0 m 的非磁化等离子体圆球后向雷达散射截面。入射波频率上限为400 MHz，等离子体特征频率为28.7 GHz，碰撞频率为20.0 GHz，3 个方向的空间步长均为5 cm，图2 所示为计算结果与文献［27］结果对比。从图中可以看出，本文计算结果与文献结果吻合较好，说明本文的PLJERC-FDTD 算法是有效的。

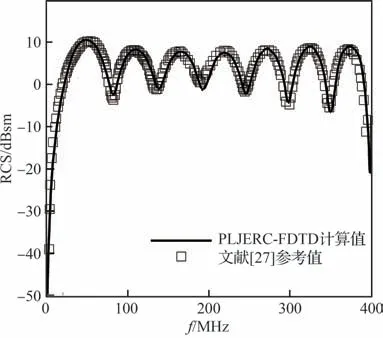
图2 计算值与参考值对比Fig.2 Comparison of calculated values with reference

2 化学反应动力学模型对等离子体流场电磁散射特性的影响

本节针对如图3 所示的类HTV-2 飞行器外形进行化学反应动力学模型影响研究，飞行器尺寸为：长2 m，尾部最大宽度0.91 m，法向最大厚度0.275 m，球头半径r=0.022 5 m。

图3 类HTV-2 飞行器外形及计算域示意图Fig. 3 Schematic diagram of HTV-2-like shape and computational domain

本节的类HTV-2 计算状态如表1 所示，PLJERC-FDTD 计算采用正方体网格对物体及流场进行划分，正方体边长为最小入射波波长的1/20，总网格数量为600 万，采用高斯脉冲波束作为入射激励源，时间步长Δt=Δ/(2c)，Δ 为网格长度，c 为真空中光速，高斯脉冲系数w=30Δt，所得RCS 数据为共极化结果。距离目标R 处的RCS 计算式为

表1 不同化学反应动力学模型下类HTV-2 飞行器计算状态Table 1 Calculation state of HTV-2-like vehicle with different chemical reaction dynamics models

式中：Ei( f )为入射波电场强度；Es( f )为散射波电场强度。

图4～图6 给出了在不同高度、马赫数、攻角和化学反应动力学模型条件下类HTV-2 本体与等离子体流场后向RCS 随频率变化曲线。

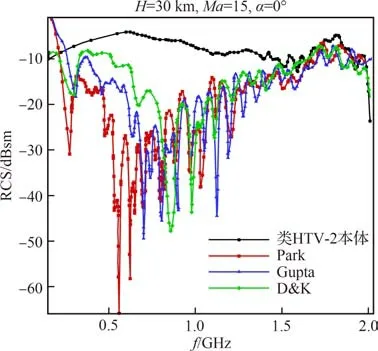
图4 30 km 类HTV-2本体与等离子体流场后向RCS 曲线Fig.4 Backward RCS curves of HTV-2-like vehicle itself and plasma flow field at 30 km

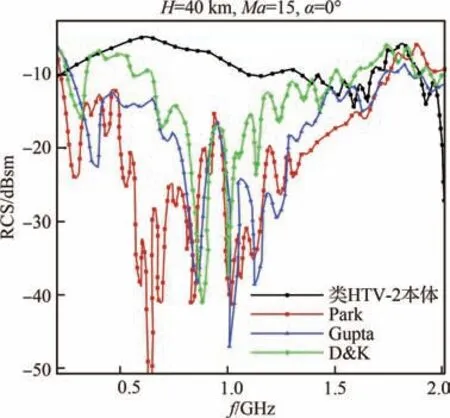
图5 40 km 类HTV-2本体与等离子体流场后向RCS 曲线Fig.5 Backward RCS curves of HTV-2-like vehicle itself and plasma flow field at 40 km

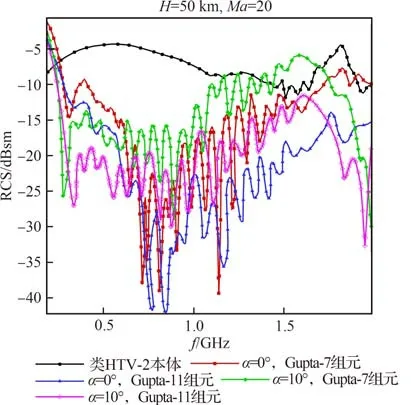
图6 50 km 类HTV-2本体与等离子体流场后向RCS 曲线Fig.6 Backward RCS curves of HTV-2-like vehicle itself and plasma flow field at 50 km

从图4～图6 可以看出，类HTV-2 飞行器的等离子体鞘套在一定程度上削弱了电磁波的传播，使得等离子体流场的后向RCS 比本体后向RCS 要小。在入射电磁波频率较低时，等离子体流场的目标RCS 大于本体RCS，等离子体鞘套对电磁波主要表现为反射作用，把目标和等离子体鞘套作为一个整体看，其反射面积增大了。随着入射波频率的增加，等离子体鞘套对电磁波的吸收作用增强，等离子体流场目标后向RCS 不断减小，并小于本体RCS。30 km 高度在入射波为0.5～0.6 GHz 左 右 时，目 标RCS 衰 减 最 大；40 km 高度在入射波为0.6～0.7 GHz 左右时，目标RCS 衰减最大；50 km 高度在入射波为0.7～0.8 GHz 左右时，目标RCS 衰减最大。入射频率继续增大，电磁波对等离子体鞘套的穿透力增强，流场的RCS 值开始上升，逐渐接近于本体RCS 值。此 外，由 于 相 对 于D&K 模 型，Park 和Gupta 模型对流场温度的预测更为准确，得到的电子数密度精度更高，因此Park 模型计算得到的电子数密度与Gupta 模型较为接近，二者均小于D&K 模型的计算结果，Park 模型和Gupta 模型得到的等离子体流场的后向RCS 值较为接近，且均小于D&K 模型的计算结果。

从图6 可得，50 km 带10°攻角状态的RCS 值略大于无攻角状态的RCS，在计算频率范围内表现为无攻角状态的RCS 值在中间频率波段相对较小，在两端较大，而等离子体流场RCS 在总体上基本均小于本体RCS。在入射波频率较低时，等离子体鞘套对电磁波主要表现为反射作用，而11 组元模型较7 组元模型对流场温度的预测偏高，11 组元化学反应动力学模型计算的电子数密度也要高于7 组元化学反应动力学模型的结果，从而7 组元模型计算的等离子体流场后向RCS要略小于11 组元模型计算的流场后向RCS。

随着入射波频率的增加，等离子体鞘套对电磁波的吸收作用增强，7 组元模型计算的等离子体流场后向RCS 大于11 组元模型计算的等离子体流场后向RCS。

图7 和图8 分别给出了不同高度和不同攻角下在入射波频率为1 GHz 时类HTV-2 飞行器本体与等离子体流场双站RCS 变化曲线。可以看出，对于180°（前向）和0°（后向）2 个双站角，类HTV-2 飞行器本体RCS 都大于等离子体流场的RCS 值，在1 GHz 频率时等离子体流场对电磁波仍然主要表现为吸收作用，在其他双站角处飞行器本体RCS 和流场RCS 交替变化，无明显规律。由图7 可以看出，前向和后向RCS 变化随高度的变化趋势相反，对于等离子体流场前向RCS，30 km 高度处最小，50 km 高度处最大；对于等离子体流场后向RCS，30 km 高度处最大，50 km 高度处最小。由图8 可以看出，有攻角状态下的等离子体流场前向RCS 要小于无攻角状态下的等离子体流场前向RCS，而有攻角状态下的等离子体流场后向RCS 要大于无攻角状态下的等离子体流场后向RCS。

图7 不同高度下类HTV-2 本体与等离子体流场双站RCS 变化曲线Fig.7 Bistatic RCS curves of HTV-2-like vehicle itself and plasma flow field at different altitudes

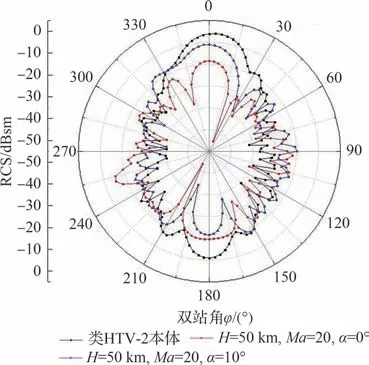
图8 不同攻角下类HTV-2 本体和等离子体流场双站RCS 变化曲线Fig.8 Bistatic RCS curves of HTV-2-like vehicle itself and plasma flow field at different angles of attack

3 湍流模型对等离子体流场电磁散射特性的影响

为考察湍流效应下高超声速等离子体流场对目标电磁散射特性的影响，本节基于由Laminar 模 型、SST（Shear Stress Transport）模 型、DES（Detached Eddy Simulation）模型和DDES（Delayed Detached Eddy Simulation）模型得到的高超声速等离子体流场数据，研究类HTV-2等离子体流场后向RCS 特性，计算状态如表2所示。

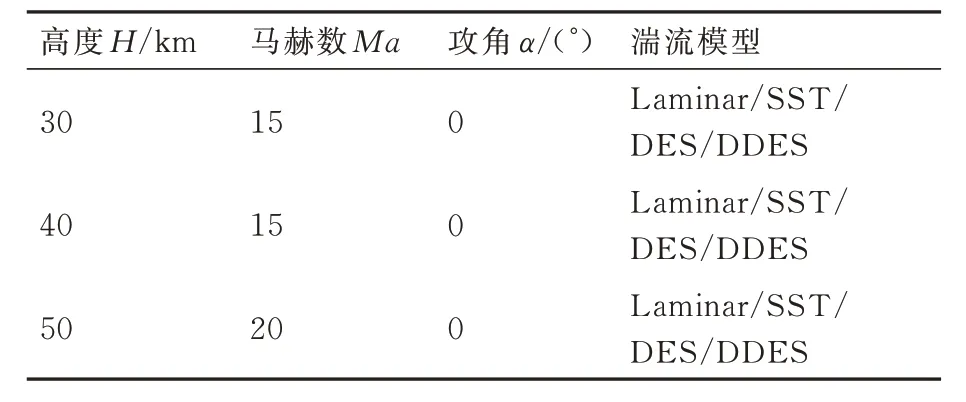
表2 不同湍流模型下类HTV-2 飞行器计算状态Table 2 Calculation state of HTV-2-like vehicle with different turbulence models

图9～图11 为不同湍流模型下类HTV-2 飞行器高超声速等离子体流场后向RCS 的变化曲线。由图可知，考虑湍流效应的高超声速等离子体流场后向RCS 基本上均小于本体后向RCS，这一点和层流流场计算结果保持一致。从后向RCS 随频率的变化来看，湍流模型影响下的高超声速等离子体流场后向RCS 随频率变化要比层流模型的结果更为剧烈，反映了高超声速等离子体湍流流场在空间结构上是不稳定的，且随着高度的增加这种特性呈减弱趋势，说明了单纯由湍流引起的不稳定性减弱，这和来流雷诺数随高度减小相符合。

图9 30 km 不同湍流模型下类HTV-2 本体与等离子体流场后向RCS 变化曲线Fig.9 Backward RCS curves of HTV-2-like vehicle itself and plasma flow field with different turbulence models at 30 km

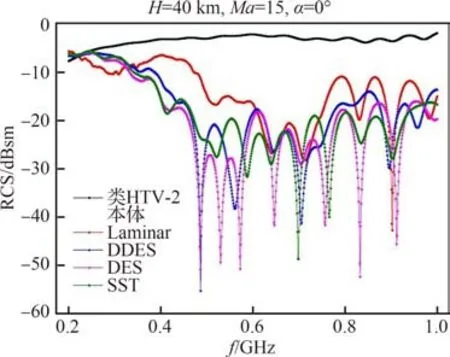
图10 40 km 不同湍流模型下类HTV-2 本体与等离子体流场后向RCS 变化曲线Fig.10 Backward RCS curves of HTV-2 vehicle itself and plasma flow field with different turbulence models at 40 km

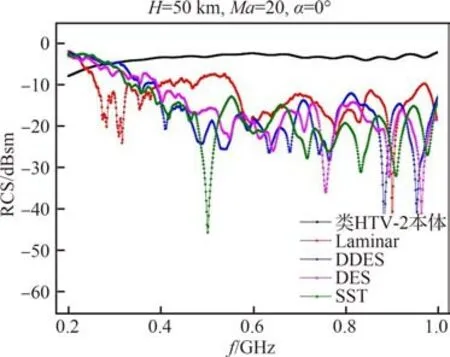
图11 50 km 不同湍流模型下类HTV-2 本体与等离子体流场后向RCS 变化曲线Fig.11 Backward RCS curves of HTV-2 vehicle itself and plasma flow field with different turbulence models at 50 km

由图9～图11 可知，在入射波频率较低时，等离子体鞘套对电磁波主要是反射作用，使得等离子体流场的目标RCS 大于类HTV-2 飞行器本体RCS，随着入射波频率的增加，等离子体鞘套对电磁波的吸收作用增强，使等离子体流场目标RCS 小于飞行器本体RCS。Laminar 模型计算的等离子体流场的后向RCS 呈现先减小后增大然后趋于稳定的趋势，这和入射电磁波随着频率增加穿透等离子鞘套的能力增强有关；而湍流等离子体流场的后向RCS 则是先减小，然后剧烈振荡，并出现一极小值后再增大并趋于平稳。此外，基于DDES 模型和DES 模型计算的等离子体流场后向RCS 较为接近，且振荡较其他模型更为剧烈，这是因为DES 模型和DDES 模型通过一个衔接函数将RANS（Reynolds Averaged Navier-Stokes equation）方法和LES（Large Eddy Simulation）方法结合，用高效的RANS 方法模拟高频小尺度运动主导的近壁面区域，而在低频大尺度运动占优的非定常分离流动区域则采用高精度的LES 方法，因此相对于Laminar 模型和SST 模型，DES 模型和DDES 模型能更精确地逼近真实物理解。SST 模型计算的等离子体流场后向RCS 略 大 于DDES 模 型 和DES 模 型，且RCS 涨落幅度较小；Laminar 模型计算的等离子体流场后向RCS 在几种模型中最大，说明层流模型不能很好地刻画高超声速等离子体流场，使得计算得到的电子数密度跟其他几个模型差异较大，从而影响了等离子体频率和等离子体碰撞频率等关键参数的计算精度，导致等离子体流场的后向RCS 结果差异很大。总的来说，考虑湍流模型的化学非平衡流场的雷达散射特性更为复杂，其后向RCS 随频率变化更加剧烈，这在一定程度上和湍流流动的不稳定性有关。

4 结 论

本文选取高超声速类HTV-2 飞行器为研究对象，基于考虑不同化学反应动力学模型和湍流模型得到的等离子体流场数据，采用PLJERCFDTD 数值计算方法，探索不同物理化学模型对高超声速飞行器等离子体流场电磁散射特性的影响，得到以下结论：

1） 在计算频率范围内，飞行器等离子体鞘套流场的后向RCS 和飞行器本体的后向RCS 随频率的增大而上下振荡变化，在入射电磁波频率较低时，等离子体鞘套对电磁波主要表现为反射作用，等离子体流场的目标RCS 大于本体RCS；随着入射波频率的增加，等离子体鞘套对电磁波的吸收作用增强，等离子体流场目标后向RCS 逐渐减小，并小于本体RCS；随着入射频率继续增大，电磁波对等离子体鞘套的穿透力增强，流场的RCS 值开始上升，逐渐接近于本体RCS 值。

2） 对于不同的化学反应动力模型，Park 模型和Gupta 模型计算得到的等离子体流场的后向RCS 值较为接近，且均小于D&K 模型计算的等离子体流场的后向RCS；在入射电磁波频率较低时，7 组元模型计算的等离子体流场后向RCS 要略小于11 组元模型计算的等离子体流场后向RCS，随着入射波频率的增加，7 组元模型计算的等离子体流场后向RCS 大于11 组元模型计算的等离子体流场后向RCS。

3） 对于不同的湍流模型，基于DDES 模型和DES 模型计算的等离子体流场后向RCS 较为接近；SST 模型计算的等离子体流场后向RCS 略大于DDES 模型和DES 模型，且RCS 涨落幅度较小；Laminar 模型计算的等离子体流场后向RCS在几种模型中最大，不能很好地刻画高超声速等离子体流场，导致等离子体流场的后向RCS 结果差异很大。考虑湍流效应的电磁散射特性较层流流场更为复杂，其后向RCS 随频率变化更加剧烈，这在一定程度上和湍流流动的不稳定性有关，且随着高度增加，湍流效应对电磁散射特性的影响逐渐减弱。