泡沫铜多孔材料的液体渗透特性研究

张晨阳 贾志海 黄宝罗 康学良

摘 要：目前对波形板汽?水分离装置的研究多集中于结构参数和入口参数的分析，而从其材料特性角度探讨提高分离效果的研究鲜有报道。以去离子水为介质，探讨了泡沫铜多孔材料孔隙率、有效半径以及浸润性对其渗透特性的影响。将修正后的弯毛细管模型与达西定律相结合，建立了泡沫铜渗透率、孔隙率以及有效半径之间的定性关系，即随着泡沫铜孔隙率和有效半径的增加，其渗透性能逐渐增强，这一结论与实验结果符合良好。此外，通过对泡沫铜材料进行浸润改性，分析了浸润性对其渗透性能的影响，结果发现，随着表面能的提高，泡沫铜的渗透性能逐渐增强。

关键词：多孔材料；渗透；孔隙率；有效半径；浸润性

中图分类号： TK124   文献标志码： A

Study on the fluid permeability of porous foam copper materials

ZHANG Chenyang，JIA Zhihai，HUANG Baoluo ，KANG Xueliang

（School of Energy and Power Engineering， University of Shanghai for Science and Technology， Shanghai 200093， China）

Abstract：Previous studies on the steam-water separator with corrugated plates usually focused on the analysis of structural parameters and inlet parameters， and there were few reports on the improvement of separation performance in terms of the material characteristics. The permeability of porous foam copper materials was investigated. The effect of porosity， effective radius and wettability on the permeability was analyzed using deionized water as the medium. Combining the modified curved capillary model with Darcy's law， a qualitative relationship among the permeability， porosity and effective radius was proposed. The permeability of foam copper gradually increases with the increment of porosity and effective radius， which is consistent with the experimental results. In addition， wetting modification changes the surface energy of foam copper. It is found that with the increase of surface energy， the permeability of foam copper ascendsgradually.

Keywords：porous material; permeation; porosity; effective radius; wettability

波形板汽?水分离器作为一种常见的汽水分离装置，由于其分离效率较高、阻力小、破膜速度高等特点，广泛应用于化工、能源以及核动力装置中。然而，研究发现，在气流扰动下，分离的液体会在波形板后端逐渐汇集成一定厚度的液膜，且随着液膜厚度的增加，临界破膜速度减小，当气流流速高于临界破膜速度时，液滴会从液膜处撕裂分离，形成二次分离液滴，使得波形板汽?水分离器分离效率显著降低［1–4］。

为了提高汽水分离效率，目前研究人员主要通过改变波形板的结构参数，如波形板的屈折角、节距、间距、单双钩等［5–7］来防止二次分离现象的产生，并取得了一定成效，但分離效率总体偏低。近年来，随着金属多孔材料的发展，越来越多性能优异的金属多孔材料被应用到超焓燃烧［8］、无光催化降解［9］以及强化导热［10］等领域。泡沫铜多孔材料由于具有孔隙率高、性质稳定、渗吸性和渗透性高等特点［11–13］，尤其适用于汽水分离领域［14–15］。为此，本文对泡沫铜多孔材料的渗透性能进行探讨，分析其结构和浸润性对液体渗透特性的影响，以期为泡沫铜多孔材料在汽?水分离领域的应用提供参考。

1 实验装置及材料

1.1 实验装置

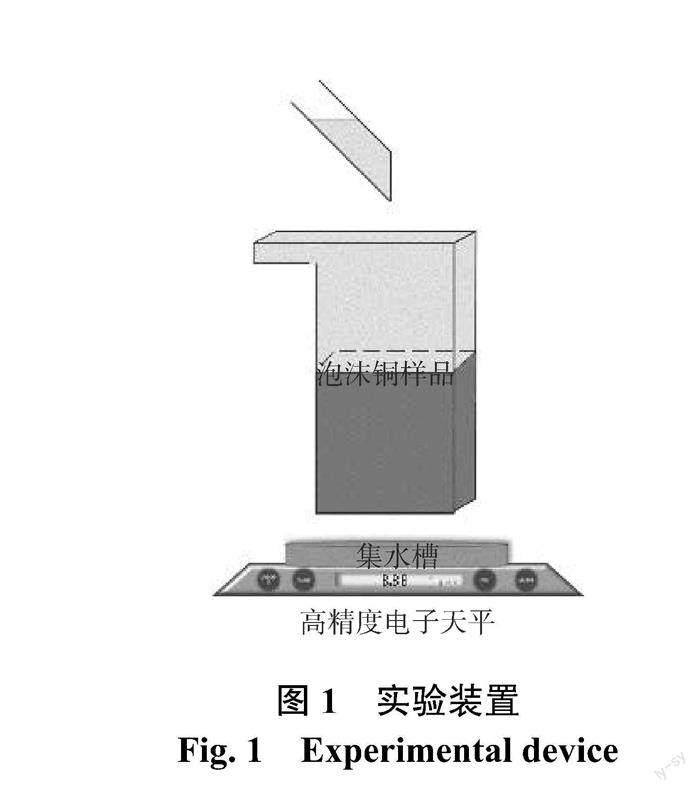
实验装置如图1所示。利用3D 打印技术得到渗流实验所需结构件，在结构件上部设置导流槽，以便将未能渗流的液体及时排走，从而保证液面高度的稳定。将泡沫铜样品从结构件底部放入并固定。通过铁架台将含有泡沫铜的结构件竖直固定，将电子天平和集水槽放置于结构件下方。电子天平最大量程为3 kg，最小精度为0.1 g。利用可调节水泵将水以合适的流量从结构件上部输入，结构件上部采用过滤网包裹，以避免流速对渗透过程产生影响。在实验过程中每隔10 s 记录渗流质量。

1.2 泡沫铜样品

为探究孔隙率Φ及孔隙有效半径 r0对泡沫铜渗透性能的影响，将样品分为4组。表1为泡沫铜样品结构参数，样品尺寸均为50 mm ×50 mm ×2 mm 。图2为利用 DinoAM7915相机获得的样品显微结构，放大倍数为100倍。可见，该泡沫铜样品为由相互贯通的五边形孔洞构成的网络结构。

2 物理模型

泡沫铜简化模型示意图如图3所示。通常采用等径毛细管模型来简化其过于复杂的内部结构。

将泡沫铜内部孔隙体积等效为 n 根半径为 r 的直毛细管体积，即用一束平行直毛细管代替真实的泡沫铜的孔隙结构。由 Hagen?Poiseuille 方程可知，通过单根直毛细管模型的流量 ql 为

式中：μ为液体动力黏度，Pa · s；L0为直毛细管长度， m ；Δp 为沿毛细管压降， Pa。

由于简化模型与实际情况相差很大，泡沫铜多孔材料中液体流道通常是非圆形且曲折的，因此，需对 Hagen?Poiseuille 方程进行修正，引入形状修正因子以及弯曲通道长度。修正后通道毛细管流量 qs 为

式中：α为形状修正因子；r0为等效弯毛细管半径，即有效半径，m；La 为弯毛细管的实际长度，m。

假设实际泡沫铜样品中孔隙通道可等价为由 n0根有效半径为 r0、长度为 La 的弯曲毛细管构成，且已知渗流过程中泡沫铜的流通横截面积为 A1，单根等效毛细管的流通横截面积为 S0=π（αr0）2，则毛细管数 n0近似为 A1/[π（αr0）2]。这样，通过泡沫铜的渗透总流量 q 为

根据达西定律，有

式中： Kd 为渗透系数，m · s?1；L 为泡沫铜上、下流经截面的距离， m ；A2为过水断面面积， m2；Δh 为上、下水头距离， m。

已知 A1=A2，将式（3）代入式（4）可得

式中：ρ为液体密度， kg ·m?3；g 为重力加速度， m · s?2；τs=La/L0为泡沫铜迂曲度。

已知渗透系数 Kd 和渗透率 k 的关系为

将式（5）代入式（6）可得

由于多孔泡沫铜的孔隙均为五边形结构，因此其形状修正因子α保持不变，且已知τs 是关于孔隙率Φ的函数，两者呈负相关，即随着Φ增大，τs 逐渐减小［16–17］，因此，式（7）简化为

式中， C 为方程常数。

由式（8）可知，泡沫铜的渗透率 k 与有效半径 r0、孔隙率Φ均正相关。

3 結果与讨论

3.1 孔隙率的影响

图4为泡沫铜的渗透质量 m 和时间的关系。从图中可知，不同孔隙率下第一组、第二组泡沫铜的渗透质量和时间均成正比，即单位时间内渗透流量的增量均保持恒定。同时，各曲线斜率不同，说明孔隙率Φ显著影响泡沫铜的渗透性能，且Φ越大，泡沫铜的渗透性能越好。

通过图4中的的数据可计算得到不同结构参数下泡沫铜的渗透流量 q，结合式（4）和式（6）得到第一组、第二组泡沫铜的渗透率 k，结果如图5所示。从图中可知：对于两组泡沫铜，当Φ为85%时， k 为1.32×10?12 m2，最小；当Φ为98%时， k 为5.31×10?12 m2，最大； k 均随着Φ的增大而增大。

对于有效半径相同的泡沫铜，孔隙率Φ的增加将导致其内部迂曲度τs 减小，从而使弯曲毛细管的实际长度 La 减小。根据式（3）可知，此时渗透流量 q 将增大，这与图4中的结果一致。随着渗透流量的增大，由式（4）可知泡沫铜的渗透系数将增加，这与式（8）的结果一致，即随着泡沫铜孔隙率的增大，渗透率也增大。

从流动阻力损失的角度进行分析，有

式中：hf 为沿程阻力损失，Pa；hj 为局部阻力损失， Pa；λf 为沿程阻力系数； l 为沿程长度， m ；d 为通道直径， m ；u 为流速， m · s?1；ξj 为局部阻力系数。

由式（9）可知，沿程阻力损失与沿程长度成正比。当泡沫铜有效半径 r0一定时，随着孔隙率Φ的增大，迂曲度τs 逐渐减小，导致沿程长度 l 变小，沿程阻力损失减小。同时，通道越趋向于竖直，局部阻力损失系数越小。由式（10）可知，局部损失减小，液体可以更加顺畅地流过，导致渗透率 k 逐渐增大。

边界层理论认为，在固体壁面附近的液体薄层中黏性力的影响不能忽略，沿壁面法线方向存在相当大的速度梯度，从固体壁面到约等于99%的外部流动速度处的垂直距离被定义为边界层厚度。边界层的产生降低了多孔材料的渗透率，边界层不易参与液体流动，只有当驱替压差达到一定程度时这部分液体才能克服黏性力参与流动。第一组、第二组泡沫铜有效半径一致，可见边界层不是影响这两组泡沫铜渗透性能的主要因素。但从图4（b）中可见，孔隙率相同时第二组泡沫铜的渗透曲线在第一组的上方。这是由于第二组泡沫铜的有效半径大于第一组，导致流体的流动阻力损失更小，且边界层对液体流动的影响也更小。

3.2 有效半径的影响

图6为不同有效半径泡沫铜的渗透质量和时间的关系。从图中可知，第三组、第四组泡沫铜的渗透质量和时间仍均成正比，即单位时间内渗透质量的增量保持恒定。同时，3条曲线斜率不同，说明有效半径会显著影响泡沫铜的渗透性能，且有效半径越大，泡沫铜的渗透性能越好。

通过图6的数据，并结合式（4）和式（6）可得到第三组、第四组泡沫铜的渗透率 k，结果如图7所示。当有效半径为0.14 mm 时，渗透率最小，为1.87×10?12 m2；当有效半径为0.50 mm 时，渗透率最大，为7.15×10?12 m2；渗透率均随着有效半径的增大而增大。

对于孔隙率相同的泡沫铜，随着其有效半径 r0增加，根据式（3）可知，此时渗透流量 q 将增大，这与图6中的结果一致。随着渗透流量 q 的增大，由式（4）可知泡沫铜的渗透系数增加，这与式（8）的结果相符，即随着泡沫铜有效半径的增大，其渗透率也增大。

从流动阻力损失的角度进行分析，由式（9）可知沿程阻力损失和直径成反比，当孔隙率Φ一定时，随着有效半径 r0的增大，流动沿程阻力损失逐渐减小，同时局部阻力损失也越小，导致渗透率 k 逐渐增大。

吸附理论认为，物质的比表面积越大，其固体表面与液体间的分子力越强，即吸附力越强，导致流动阻力增大，渗透率减小。由图2可知，当孔隙率不变时有效半径越小，构成泡沫铜孔隙的微通道越细，通道数目越多，导致其比表面积越大，液体与泡沫铜表面间的分子力也越大，这将阻碍液体的流动，导致其渗透率减小。

从边界层角度进行分析，第三组和第四组泡沫铜的孔隙率基本保持一致，但有效半径存在较大差别。泡沫铜的有效半径越小，边界层对液体流动的影响越明显，因此渗透率越小。

3.3 浸润性的影响

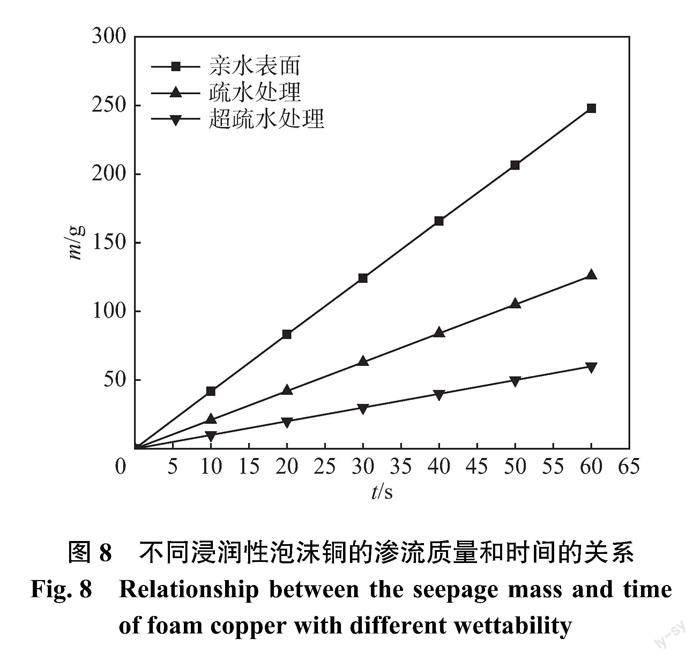
对Φ=92%、r0=0.19 mm 的泡沫铜表面进行浸润改性，测试亲水表面（原表面）、疏水表面（经稀 HCl 多次处理）和超疏水表面（经 GLACO 含氟防雨剂多次处理）的渗透特性，结果如图8所示。从图中可知，亲水表面的渗透流量最大，即渗透特性最好，其次是疏水处理的表面，而超疏水处理的表面渗透特性最差。

实验中通过浸润改性方法，改变泡沫铜表面的表面能大小，其中亲水表面的表面能最大，其次是经稀 HCl 疏水处理的表面能，而经超疏水处理的表面能最小。根据吸附理论可知，表面能越大，液体与泡沫铜表面的分子间作用力就越大，在泡沫铜结构以及比表面积不变的情况下，亲水表面（原表面）的渗透性能最好，而超疏水表面的渗透性能最差，这与实验结果完全一致。

进一步分析可知，当泡沫铜进行超疏水改性后其表面能最小，此时液体与泡沫铜表面之间的界面张力差最大，而界面张力是影响液体界面形状的关键因素，当外界施以压力梯度时，界面张力的大小决定液滴能否形变到足以通过弯曲的孔道，而刚好能使液体通过孔道的压力梯度称为启动压力梯度。因此，通过浸润改性后，超疏水泡沫铜的启动压力梯度最大，导致一部分微孔道无法被液体渗入，使其渗透性能最差。

4 结论

以去离子水为介质研究了泡沫铜多孔材料结构参数和浸润性对渗透性能的影响。主要结论为：

（1）随着泡沫铜孔隙率的增加，液体流动过 程中的流动阻力损失变小，导致泡沫铜的渗透率 从孔隙率为85%时的1.32×10?12 m2增加到孔隙 率为98%时的5.31×10?12 m2，渗透性能逐渐增强。

（2）随着泡沫铜有效半径的增加，液体流动过程中的流动阻力损失变小，同时比表面积减小，吸附力随之减小，且边界层对液体流动的影响也越小，导致泡沫铜的渗透率从有效半径为0.14 mm 的1.87×10?12 m2增加到有效半径为0.50 mm 的7.15×10?12 m2，渗透性能逐渐增强。

（3）泡沫铜多孔材料的表面能越小，所需的启动压力梯度越大，液体越难渗入孔道。经过疏水、超疏水处理过的材料与原亲水泡沫铜材料渗透性能的对比实验表明，超疏水处理的泡沫铜渗透性能最差，而原亲水表面渗透性能最好。

参考文献：

［1］臧丽叶， 田瑞峰， 孙兰昕， 等.横掠气流作用下波形板壁降膜破裂分析[J].化工学报， 2014， 65（3）：862-869.

［2］沈俊杰， 童小忠， 乔宗良， 等.折流板除雾器内液滴运动和分离特性的数值研究[J].热能动力工程， 2020， 35（3）：173-180.

［3］毛峰， 田瑞峰， 陈怡炫.波形板干燥器内壁面液膜破裂临界条件的实验研究[J].原子能科学技术 ， 2018， 52（5）：855-861.

［4］ WANG B， TIAN R F. Investigation on flow and breakdown characteristics of water film on vertical corrugated plate wall[J]. Annals of Nuclear Energy， 2019， 127：120-129.

［5］朱雁凌， 王啸宇， 游尔胜， 等.双钩波形板汽水分离器 疏水钩优化研究[J].原子能科學技术， 2021， 55（10）：1780-1787.

［6］王进卿， 池作和， 张光学， 等.双钩波形板分离器的冷态试验研究[J].流体机械， 2012， 40（3）：8-11.

［7］张恩实， 王飞飞.冷却塔折流板除雾器叶片折角优化数值模拟[J].流体机械， 2018， 46（7）：69-75， 53.

［8］舒文静 ， 郭雪岩.多入口多孔介质燃烧器的数值模拟[J].能源研究与信息， 2017， 33（2）：112-117.

［9］张熙， 李生娟， 索路路， 等. ZnO/Zn/CNT 三维多孔复合结构的制备及对甲基橙的无光催化降解[J].上海理工大学学报， 2016， 38（4）：335-340.

［10］孙金祥 ， 杨丽红.等温容器内多孔介质强化导热研究[J].能源研究与信息， 2013， 29（1）：53-56.

［11］赖展程， 胡海涛， 庄大伟， 等.泡沫金属结构对排水性能的影响[J].化工学报， 2016， 67（7）：2756-2760.

［12］黄豆， 贾力.烧结铜粉吸液芯毛细性能研究[J].工程热物理学报， 2021， 42（2）：494-503.

［13］蒋玉婷， 张鹏， 吕凤勇.采用易挥发工质对超亲水泡沫铜的毛细性能表征[J].上海交通大学学报 ， 2019， 53（11）：1294-1301.

［14］ XU Y C， YANG Z M， ZHANG J S. Study on performance of wave-plate mist eliminator with porousfoam layer as enhanced structure. Part I： Numerical simulation[J]. Chemical Engineering Science， 2017， 171：650-661.

［15］ XU Y C， YANG Z M， ZHANG J S. Study on performance of wave-plate mist eliminator with porous foam  layer  as enhanced structure.  Part  II： Experiments[J]. Chemical Engineering Science， 2017， 171：662-671.

［16］ FU J L， THOMAS H R， LI C F. Tortuosity of porous media： image analysis and physical simulation[J]. Earth-Science Reviews， 2021， 212：103439.

［17］ XU P， YU B M. Developing a new form of permeability and Kozeny– Carman constant for homogeneous porous media by means of fractal geometry[J]. Advances in Water Resources， 2008， 31（1）：74-81.