培养提问能力 发展推理意识——“有关0的运算”教学实践与思考

文|张国梅 俞 杰

与0 有关的运算，在人教版数学教材里，三年级及之前的学习中，学生就已多次遇到过。“一个数加（减）0 等于原数”“0 和任何数相乘都得0”“0 除以任何不是0 的数都得0”，这些结论（运算规则），借助具体情境的支撑，学生较容易接受和理解。但学习第三个结论时，学生心中是有疑问的：除数为什么要“任何不是0 的数”呢？

学生有这样的疑问是好事情，是批判性思维的萌芽。但是，课堂上学生不见得有机会提出来，即使提出来，教师也往往会以“这是规定”或“以后你就会知道原因”等理由来应对，并再次强调“要记住，0 不能作除数”。

教师“屏蔽”学生的问题也并非没有道理，因为学生的思维水平还未到合适时机，教材也是因为如此考虑，而将相关内容设置在了四年级下册“四则运算”单元，且特意编制一道例题教学“有关0 的运算”。（如下图）

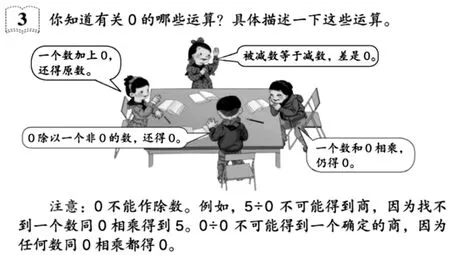
该题对0 的四则运算作了集中呈现，并指出了“0 不能作除数”的两个原因。仔细阅读例题图文后，我们意识到，这个例题是一个绝好的教学契机，既可激发学生提出有意义的数学问题，得到提问能力的培养，又可借此引发高质量的数学思考，获得推理意识的发展。

为何该题会有如此功效？从图中可见，与0 有关的结论，加减乘除中都有，且不止这四个。之前这些结论，都是单个单个学的，没有相互比较的机会，而如今，四个结论一起呈现了，那么它们表述上的明显差异，就一定会促使学生自觉地进行比较。比较之后，从差异处引发的丰富问题一定会自然产生，包括之前曾经疑惑过的“除数为什么不能是0”。要理解此结论，学生不能再依托生活情境来分析，而是要从数学的角度，借助被除数、除数、商之间的关系，运用假设法来反推出商的具体情况，这样才能获得深度理解。

【教学实践】

一、教学引入

1.直接揭题，口算热身

板书课题“有关0 的运算”，逐题板书题目，引导学生边口算边理解课题含义。

3+0=0+99=5-0=

17-0=4×0=0×7=

0÷4=0÷3=

2.回忆旧知，唤醒经验

（1）经验分享

师：同学们都算得非常快！那么做这些题目，你有什么经验能介绍吗？

根据学生回答，教师在算式右边相对应位置，板贴逐条呈现学生的经验：一个数加0 等于原数；一个数减0 等于原数；一个数乘0 等于0；0 除以一个不为0 的数等于0。

（2）原理解释

师：为什么一个数加0 等于原数？

生1：0 表示没有，所以加0还是原数。

生2：0 表示没有，一个数减0，也就是没减，当然也等于原数。

师：那为什么一个数乘0 等于0？你能不能选一个算式为例来说明？

生1：因为0 就是没有，比如4×0 就是4 个0 相加，还是等于0。

生2：4×0 也可以想成0 个4，那也是等于0。

师：除法呢？

生：比如0÷4，表示0 个物体平均分成4 份，结果肯定还是0。

师：这些规则其实原来我们都已经学过，大家也明白这些规则背后的道理，这节课就让我们更深入地来思考新的问题吧。

二、新知探索

1.学生提问

师：请同学们仔细观察黑板上这四条运算规则和四组算式。关于0 的运算，你心中有没有产生一些疑惑或者感兴趣的问题？

生：为什么0 只能除以一个不为0 的数，而不能除以0 呢？

师：好问题！这位同学敢于质疑结论，对这句话中的关键词提出了自己的疑问。

生：为什么是0 除以一个不为0 的数而不是一个不为0 的数除以0 呢？

师：你能举个例子吗？

生：比如说，0÷3 倒过来变成3÷0，这样可以吗？

师：能够倒过来想，这是逆向思维，非常棒！

师：有的同学对结论提出质疑，有的同学从算式里面发现问题。有了问题，我们就有了研究的方向，接下来让我们一起来研究这些问题吧。

2.探究释疑

（1）研究3÷0

①猜想结果

让学生猜测计算结果，大部分同学认为是0，也有认为是3，或者认为算式不成立，没有答案。

②自主探究

组织学生根据各自的结果，画一画、写一写，想办法说明。

③汇报方法

生1：有0 元钱，要平均分给3 个人，每人分到0 元，所以答案是0。

生2：3÷0 就是把3 平均分成0 份，就是相当于不分，所以答案是3。

生3：3÷0 没有答案，因为除法可以用乘法来解答，但是0 乘任何数都等于0，所以这道题没有答案，算式不成立。

师：请大家讨论一下，谁的理由正确，谁的理由不对呢？

生：第一位同学说“0 元钱平均分给3 个人，每人0 元”，如果按照他的意思，算式应该是0÷3而不是3÷0。

师：那么第二位同学的说法是不是就对了？

（有的学生认为对，但有的学生反对“3”这个答案，但是又觉得没有反驳生2 的理由）

师：那我们一起做个小游戏，边玩边思考吧。

教师拿出3 支粉笔，请3 位同学协作表演。3 支粉笔，平均分给3 个人，3÷3，每人1 支；如果平均分给2 个人，3÷2，每人1 支半；如果分给1 个人，3÷1，可得3 支；最后，没有人了……

师：如果没有人，就根本无法分，更不存在每人拿到几支的说法。所以，答案是3 是不对的。

师：那我们再来讨论第三位同学的说法吧。赞成他观点的同学能不能再来详细说明一下？

学生上黑板写了：3÷0=⎰。并解释道“商乘除数等于被除数，⎰中不存在这样的一个数，乘0后得3”。教师借助板书，将商和除数连线示意（强调“假设”），并写出假设后进行思考的算式（如图）。师生对话，引导其他学生看懂如此推理的过程，并请所有学生在本子上像这样自己写一写、说一说。

师：的确，通过推理，我们发现找不到一个数乘0 等于3，所以3÷0 这个算式根本没有答案，我们也可以说这个算式没有意义。

（2）研究0÷0

①自主尝试

师：现在我们来研究第二个问题。0÷0，你能不能借用刚才这样的思考方法，先假设，再推理，试着研究研究。

学生探究，同桌交流。

②汇报展示

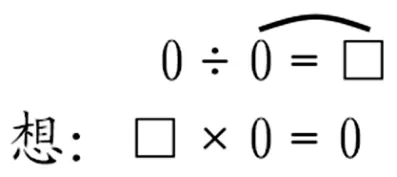
通过反馈，学生理解到此题的情况很特别：任何数乘0 都得0，所以这个算式的答案不唯一。

③教师引领

师：是的，一个除法算式，却有无数个答案，结果不确定，那这样的算式同样没有意义。

④归纳小结

教师引导学生回顾3÷0 和0÷0，使学生看到两个算式“无意义”的不同情况，同时归纳提炼出“0不能作除数”。

三、课堂总结

回顾“发现和提出问题，分析和解决问题”的过程，强调“推理”的重要意义。再次引导学生提出新的问题，感受提问的价值，适度研讨问题。

【课后思考】

非常简单的数学内容，却展现出了出人意料的教学效果。分析其原因，那就是课前所预想的“培养提问能力、发展推理意识”两大素养目标的较好达成。

1.材料精设，点拨恰当

有意义的数学问题往往藏在现实或数学的情境中，需要学生以敏锐的眼光或个性的思维才能“看”出来。因此，设计好的学习情境，本质上是在训练学生用“数学的眼光”发现问题的能力。在本课中，我们精心设计了学习材料（四组口算题、四条运算规则及其呈现方式），有意将很多可比较、可质疑、可联想的元素蕴藏其中，以此“诱发”学生萌生批判性思维、创造性思维、发散性思维，自主发现有意义的数学问题。

学生发现了问题，还需要以勇气和智慧，清晰准确地表达出问题（即提出问题）。对学生提问的回应，是提问能力培养的重要契机。在本课中，学生提出了好问题，教师并没有止步，而是以一系列行为予以跟进：让其他学生再来表述这个问题，以指向精准的评价语表扬学生的提问，用简单的文字和符号记录下问题，鼓励学生再提其他的问题。这样的做法，就是在点拨其他学生感受好问题的特征，引导更多学生明晰提问的方向和方法，大胆积极地提问。如此做法，使学生对提问方法获得了深刻感悟，提问能力得到了切实提升。

2.过程合理，指导到位

发展小学生的推理意识，需要借助具体的推理活动，需要依托合适的学习过程和教师的精心指导。本课中学生所提的问题（主要是3÷0 和0÷0），都是富含推理元素的好素材，问题的解决直接指向推理意识的发展。但是，这两个问题虽形式相似，内涵上却有区别（一个是没有答案，一个是有无数个答案），从推理的角度来说有难易之分。因此，课堂上有意设计成两个过程：先是抽象度略低一点的3÷0，并且分两个层次展开（先用以前的方法解释，再用“假设”的方法分析）；再是抽象度更高的0÷0。如此过程，从“旧经验说理→感受推理→运用推理”，学生的思维活动（推理）是真实发生、拾阶而上的。

在两次推理活动中，教师及时讲解、示范和帮助，促使每一位学生真理解、能运用。如当学生提出3÷0=⎰来作解释时，为让更多学生进入这样的思维模式，教师及时用板书将商和除数连线示意，强调“假设”并写出假设后进行思考的算式；然后通过师生对话，引导其他学生看懂如此推理的过程，并请所有学生在本子上像这样再写一写、说一说……正因为有如此到位的指导，所以当学生面对0÷0 时，他们就能够自己开展清晰的推理并作出准确的解释。学生推理意识的发展，也在这样的学习活动中显露无遗。

一个极简单的教学内容，却因内涵的彰显而焕发亮丽色彩，这再次让我们意识到：在新课程强调核心素养的背景下，我们要更深入地挖掘教材，更科学地设计教学，更好地服务于学生核心素养的发展。