小学高年级发展数学建模三部曲
——以《钉子板上的多边形》教学为例
文|相 辉
《数学课程标准(2022 年版)》明确指出:“模型意识主要是指对数学模型普适性的初步感悟。知道数学模型可以用来解决一类问题,是数学应用的基本途径;模型意识有助于开展跨学科学习主题,增强对数学的应用意识,是形成模型观念的经验基础。”挖掘教材中蕴含的数学模型,引导学生经历模型建立和求解的过程,能够发展学生的模型意识,增强学生对数学学习的兴趣,提高应用意识和实践能力。
苏教版教材中蕴含着丰富的建模内容,其中五年级上册《钉子板上的多边形》一课具有独特的价值。小学高年级阶段,学生遇到的数学问题相对比较“规范”,建模的过程往往比较顺畅。但是,钉子板上多边形的面积却大有不同。它不仅涉及图形的面积和边上钉子数这两种数量,还与图形内部的钉子数有关,关系相对复杂、比较隐蔽,在初建结构时学生很难完整把握,需要对模型进行修正、优化。这在小学阶段的建模教学中比较少见,对发展学生的科学探究精神、理解模型假设和模型检验的价值,获得较为完整的建模经验具有重要的意义。
基于以上认识,笔者认为,在教学《钉子板上的多边形》一课时,教师要抓住模型的初建、修正、优化三个阶段,精心设计教学活动,丰富学生的感知和思维体验,将这节课对发展模型思想的价值发挥到最大。
一、引导学生合情猜测,初步建立模型
小学生在建构数学模型时,通常需要经历“观察猜测,推理验证”的探究过程。观察猜测是建模的第一步。学生的猜测是基于已有的认知或直觉做出的“合情假设”。教师要给予学生观察、操作、数据的收集与比较的空间和时间,在此基础上,激发学生依据目前已有的资料和分析做出合情猜测,这种初步构建的数学结构才可能更为接近准确的模型。
师:以前在认识图形时,我们用钉子板围过一些图形,今天用点子图代替钉子板。我们约定:每个小正方形的边长都看作1 厘米。你能在点子图上画一个多边形吗?这个多边形的面积是多少?你是怎样得到的?
学生画图并交流多边形的面积计算方法,明确计算多边形的面积时可以数一数,也可以算一算。
师:今天,我们要研究钉子板上的多边形面积的规律。想一想,钉子板上的多边形面积可能会与什么有关呢?
生:我觉得可能会和图形边上的钉子数有关。我们在钉子板上围图形,感觉经过的钉子数越多,图形内部就越大。
师:有一定道理,是不是与钉子数有关?有什么关系?下面我们来一起研究。
学习活动一
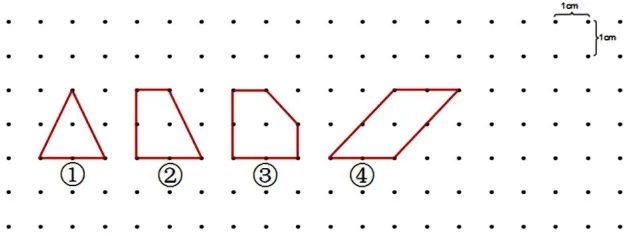
学习提示:
1.独立填写:上图中4 个多边形的面积各是多少平方厘米?每个多边形边上的钉子各有多少枚?填写在下表中。
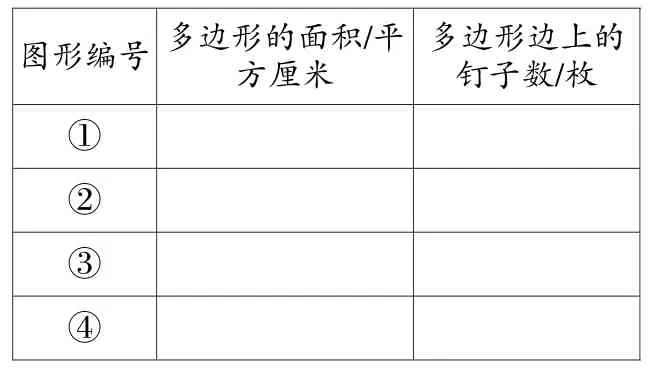
图形编号多边形的面积/平方厘米多边形边上的钉子数/枚①②③④
2.独立观察并思考:表中多边形面积的大小和多边形边上的钉子数,你有什么发现?
3.小组交流:核对表中数据,讲明是怎么得到的,并说一说你的发现。
生:我们组发现,多边形边上的钉子数越多,围成图形的面积越大。
生:我们组还发现,多边形面积的平方厘米数是多边形边上的钉子数的一半。
师:谁和他们有同样的发现?真了不起,数学讲究简洁,有什么更简洁的方法表示这个规律吗?
生:可以用字母表示。
师:用字母表示是个好方法。若用字母n 表示多边形边上的钉子数,用字母S 表示多边形的面积,那么这个关系应该表示为S=n÷2。
上面这一环节,教师先后引导学生进行两次猜想。第一次猜想建立在学生过去围多边形、计算多边形面积的经验和空间直觉的基础上,让学生猜一猜“你认为钉子板上多边形的面积会与什么有关”。教师不但鼓励学生大胆猜想,还要求学生适当做出解释,使学生初步感悟猜想也要有所依据。第二次猜想,学生数或计算出所给图形的面积,完成第一次数据收集,然后通过观察、比较发现现有数据之间的关系:多边形的面积=边上钉子数的一半,形成了初步的数学模型。
二、鼓励学生大胆质疑,在“回望”中修正模型
观察猜想,虽然基于一定的材料和经验,但往往是通过举例、观察、实验等直观而不严谨的方法得出的,导致有的猜想正确,有的猜想错误,因此猜想之后还要验证。只有检验的结果比较符合实际,满足问题所需要的精度,才能认为所建模型可以使用。否则,还需要回到建模的最初环节,重新进行模型假设和检验。
师:规律这么快就被同学们发现了,还有什么疑问吗?
生:我们是从上面4 个图形发现的结论,所有钉子板上围出的多边形都符合这个结论吗?
师:是不是所有的多边形都符合这个规律?其实,仅从4 个多边形得出结论是远远不够的,需要通过大量的多边形来验证。下面我们就来研究:这个规律对于你刚才所画的多边形适用吗?
学习活动二
学习提示:
1.研究自己画的多边形。
S=( )cm2,n=( )枚,是否符合规律?符合( )不符合( )
2.再次观察多边形①②③④,它们有什么共同点?在小组内进行交流。
生1:我画的图形符合规律,我发现只要图形内部只有一枚钉子,就符合规律。
师:大家同意吗?还有谁画的多边形也符合这一规律?内部有几枚钉子?
师:当围成多边形的内部只有1 枚钉子时都符合。当内部不是1 枚钉子时,是不是都不符合这个规律呢?
师:我们发现:钉子板上围成的多边形面积不仅与多边形边上的钉子数有关,还与围成的多边形内部的钉子数有关。看来,我们刚才发现的规律不够准确,需要修改一下,怎样修改呢?
生:当内部只有一枚钉子时,S=n÷2。
师:能更简洁吗?
生:用a 表示内部钉子枚数,当a=1 时,S=n÷2。
这一环节,教师通过提问,引导学生大胆质疑。刚才我们仅仅通过4 个实例就总结出了规律,是不是所有的多边形都符合这个规律?从而激发学生举更多的实例来验证的欲望,然后顺其自然引出活动二“研究自己画的多边形”,这时只要有学生举出反例,通过对比就可发现这一规律仅在内部有一枚钉子时成立,进而发现刚才找到的规律需要修正。
过去的学习中,学生虽然已经多次经历“猜想—验证”的过程,但验证的猜想都是正确的,导致学生误认为验证可有可无。教师充分用好前期初建的数学模型,引导学生大胆质疑,审慎帮助学生深刻体会验证的意义,理解“模型假设—模型检验”的必要性。
三、启发学生异中求同,在抽象概括中优化模型
数学模型反映的是一类问题在数量关系和空间形式上的共同规律。模型思想要求我们从解决一个问题,拓展为解决一类问题。也就是在建模的过程中,尽可能引导学生从具体情况出发,分析概括共同要素,将具体的量的关系概括在一个数学公式之中,使模型更具有一般性和统摄性。
师:看来,多边形的面积不仅与边上的钉子数有关,还与图形内部钉子数有关。当内部钉子枚数为1 时,多边形的面积S=n÷2。当内部钉子数不为1 时,这个表达式就不能用了。我们该怎么办?
生:我们还要分别研究当内部钉子数是2 枚、3 枚……时,图形面积又会与边上钉子数有什么关系?
生:我们可以看看它们是不是有什么共同的规律。
学生依次得出:
当a=2 时,S=n÷2+1,也和边上钉子数的一半有关。
当a=3 时,S=n÷2+2。
当a=4 时,S=n÷2+3。
在老师启发下得出:当a=0时,S=n÷2-1。
师:通过刚才的研究,我们发现内部钉子数是2、3、4 甚至内部没有钉子时,多边形面积与钉子数之间的关系。这些规律看起来不同,但有没有共同的地方呢(提示:既要竖向比一比,也要横向进行比较)?
学生经过讨论发现:求多边形的面积都需要用边上的钉子数÷2 再加上一个数,加上的这个数总比内部的钉子数少1。
师:如果假设多边形内部的钉子数为b,能用一个式子表示出刚才的规律吗?
学生通过讨论得出:S=n÷2+b-1。
师:这个公式,就是著名的皮克定理。大家太厉害了,和奥地利著名数学家皮克的发现完全一样。
学生通过举例验证,运用不完全归纳的方法发现了当内部钉子数分别为0、1、2、3、4 时,多边形面积与相关钉子数之间的关系,得到了不同的公式。然而本节课的探究学习并没有止步于此,教师又根据班级学生的实际情况,大胆引导学生进行进一步的探索:这些不同的公式有什么相同的地方?学生通过观察、比较、分析、讨论,发现了不同公式的共同特点,得到了更具一般意义的“通用公式”。
对学生而言,探索钉子板上多边形面积奥秘的历程,是一次体验丰富的建模过程。通过对模型的三次建构,深刻体会到“模型假设—模型建立—模型检验”的必要性,最终获得简洁而又更具一般化的数学模型,让学生忍不住感叹数学的精妙,自然流淌出对模型力量的叹服,模型思想在经历与反思中不断拔节生长!

