两种交换排序算法的分析比较

李家宏，孙庆英

(1.淮阴师范学院，江苏 淮安 223300；2.淮阴师范学院，淮安市大数据智能计算与分析重点实验室，江苏 淮安 223300)

0 引言

1 排序的定义及分类

排序(sort)就是把一组杂乱无章的数据记录或元素，按照一定的关键码重新排列成有序的序列。假定给定记录序列有n个记录(R1,R2,...,Rn) ,它们的关键码分别为(Ks1,Ks2,...,Ksn) ,排序的过程就是将这些记录排列成顺序为(Rs1,Rs2,...,Rsn) 的序列，使得相应的关键码满足Ks1≤Ks2≤... ≤Ksn（升序或非降序）或Ks1≥Ks2≥... ≥Ksn（降序或非升序）[1-2]。

排序按照数据存储的介质分为内部排序和外部排序。内部排序是数据元素全部放在内存中的排序。外部排序是数据元素太多无法同时存放在内存中，根据排序过程的要求，在内存和外存之间多次交换移动数据的排序。在本文中，主要涉及的排序算法均为内部排序算法[3]。

对于内部排序依据不同的排序原则，一般分为插入排序、选择排序、交换排序、归并排序四大类，结合目前比较经典的7大排序算法：直接插入排序、希尔排序、起泡排序、快速排序、简单选择排序、堆排序、二路归并排序[4]。具体分类如图1所示。

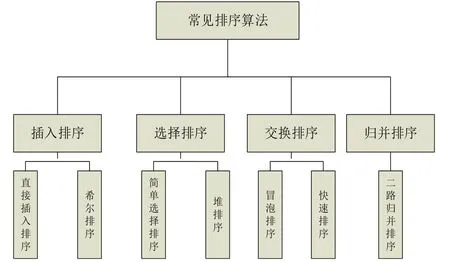
图1 常用排序算法分类

由于排序的类别较多，各种排序的原理原则不尽相同，本文主要以交换排序为例来简单分析一下排序算法。

2 交换排序的算法及实现

交换排序，顾名思义就是基于“交换”思想的排序。即通过对序列中元素进行两两比较来判断是否符合排序要求，如果不符合就交换他们之间的位置来达到满足排序的目的。假定在待排序序列中选取两个元素Ri和Rj，若满足i＜j且Ri＞Rj则通过交换Ri和Rj的位置来实现满足排序要求实现Ri＜Rj，完成排序过程。交换排序的主要方法有冒泡排序和快速排序。

2.1 冒泡排序

冒泡排序就是在排序交换过程中，类似水冒泡。较大的数往下沉、较小的数类似气泡一样往上冒，小（大）的元素数据经过不断的交换，整个过程就像冒泡一样，最小值元素一直往上“冒泡”，所以称为冒泡排序(Bubble Sort) 。

冒泡排序算法的基本思想：对序列中相邻的两个元素进行比较，如果符合排序要求就保持不变，如果不符合排序要求，就进行位置交换。通过重复循环访问序列，直到没有可交换的元素为止，整个序列排序完成。冒泡排序每一趟排序结果只能确定将一个数归位，即第一次排序的结果将序列的末位上的数确定，第二次排序的结果将序列的倒数第二位上的数确定，以此类推，假设有n个数进行排序，则需要进行n-1 次的排序操作。第1 次排序，通过“冒泡”，将前n个元素中最大的值移动到序列的最后一位，这轮排序结束后就剩下前n- 1个元素未排序。第i次排序，此时剩余前n-i+ 1个元素未排序，通过“冒泡”，将前n-i+ 1个元素中最大的值移动到剩余序列的最后一位。最后第n- 1 次排序，只剩余2 个元素未排序，将其中较大的值移动到后一位，整个排序完毕[5]。冒泡排序的基础算法如图2。

图2 冒泡排序的基础算法

通过对上述程序算法分析不难发现，对于有些排序序列在经历过几次遍历之后就达到了排序要求，但程序还继续执行，继续进行遍历，从而浪费了计算机资源。从冒泡排序算法交换排序思想中，不难发现判断冒泡排序的结束条件应该是一趟排序过程中有无进行交换的操作。为此，为了优化冒泡排序，很多时候我们在每趟排序开始前设置标志，用来记录每轮遍历过程中是否有数据交换发生，如果有交换发生继续执行下一次，如果没有发生数据交换直接可以判断整个冒泡排序已经完成。改进的冒泡排序算法如图3。

图3 改进冒泡排序算法

2.2 快速排序

快速排序(quick sort) 是对冒泡排序的一种改进。冒泡排序中每次比较相邻的两个数据，每次交换只能移动一个位置，导致在程序的执行过程中比较次数和移动的次数均较多。为了减少比较和移动的次数，快速排序中采取了比较和移动从两端向中间进行，值较大的数据一次就能从前面移动到后面，反之值较小的数据也能一次从后面移动到前面[6]。

导致华盛顿没有积极因应缅甸提出的各种安全、军援诉求，首先是当时美国的东南亚政策目标所致。鲁塞尔·法菲尔德认为，1899—1954年，美国在东南亚的政治经济利益是有限的。美国只是对东南亚的事件做出反应，而不是主动地影响这个地区的发展，美国在东南亚的目的以促进各国内部稳定和集体安全为中心。[35]美国在缅甸的政策目标是，援助缅甸，帮助其实现国内的稳定和社会经济发展，倒向美国，防止其成为一个共产党国家。1954年之前，美国在东南亚区域和缅甸的政策目标决定其对缅甸的各种援助诉求反应有限。

快速排序采用的是分治思想，即在一个无序的序列中选取一个任意的基准元素pivot（一般为该序列的第一个元素或者中间元素），利用pivot 将待排序的序列分成两部分，前面部分元素均小于或等于基准元素，后面部分均大于或等于基准元素，然后采用递归的方法分别对前后两部分重复上述操作，直到将无序序列排列成有序序列。

假设有一待排序序列R，设数据元素序列最低为first,最高位为last，其中first＜=last，则该序列可以将数据元素存储在R[first]～R[last]中。选取第一个元素作为基准元素 即pivot=R[first],设置区域划分令i=first,j=last。开始右侧遍历，找到小于等于pivot的数，如果找到R[i]和R[j]交换，i++;开始左侧遍历，找到大于pivot 的数，如果找到R[i]和R[j]交换，j--。重复执行上述操作，直到i与j重合，返回该位置的数正好是基准元素pivot 元素。经典快速排序的算法如图4。

图4 经典快速排序算法

经典快速排序算法由于每次总是固定选取第一个元素作为基准元素，这样会导致每次依据基准元素划分出来的两个序列极其的不平衡，尤其对于完全有序序列，快速排序每趟结束后，基准元素pivot 处于边缘，形成一个为空，一个只比上次少一个元素的子序列，最终使得快速排序算法退化为冒泡算法。为了避免这种情况的发生，对经典排序算法做了一定的改进，目前常用的有以下三种方法。

随机选择法即在序列的下标第一位first和最后一位last之间的所有元素中随机选取一位元素作为基准元素pivot。这种方法最大限度地避免了选到序列中最大或最小元素作为基准元素，但由于随机选取，这与排序数据的分布和运气有关，不易控制。

三数取中法即取序列的下标第一位first、最后一位last及下标为(first + last)/2这三元素的中间值作为基准元素pivot。由于此法取到的中值不是最值，虽然不能保证每次划分的完全平衡，但基本上避免了出现极度不平衡。

还有一种不常用的九数取中法即从序列中分3次随机取样，每次取样3个，从每次取样的3个中选取中间数，然后再从这3个中间数中取出中间数作为基准元素pivot。这种取法大概率能保证每次划分的平衡，但由于多次使用随机函数增加系统开销。

3 两种交换排序算法的比较

排序算法的性能取决于算法中比较和交换的次数以及是否需要额外的空间用于存放临时值，也就是算法的时间复杂度和空间复杂度。

冒泡排序算法的时间复杂度由执行排序过程中的遍历数决定，即外循环和内循环以及判断和交换元素的时间开销。最优的情况是排序序列为正序序列，只需要遍历不需要数据交换，正常的比较次数为[n*(n- 1) ]2,则时间复杂度为O(n2),但优化后的冒泡排序设置了标志位来判断是否排序好，则此时只需要进行n- 1 次比较，则时间复杂度为O(n)。反之如果排序序列为反序序列，每一次都要交换两个元素，时间花费为[3*n*(n- 1) ]2 ,则时间复杂度为O(n2),由于在冒泡排序中涉及交换的操作肯定多，所有冒泡排序的平均时间复杂度为O(n2)。冒泡算法的空间复杂度主要是元素交换过程中所用的临时变量所占用的空间，如果是正序序列不需要交换数据则空间复杂度为0,如逆序则为O(n),平均空间复杂度为O( 1)。

快速排序算法的时间复杂度由执行的递归算法的复杂度决定，即递归深度决定。最优的情况是基准元素pivot 每一次划分后，左右两侧的序列长度相同，此时采用递归算法的时间复杂度计算公式为：T[n]=2T[n2 ]+f(n),其中T[n2 ]为平分后序列的时间复杂度，f[n]为平分这个序列所花的时间。采用迭代法依此推算，平分到最后不能再平分，已迭代完得到了T[n/(2m)]=T[1] (T[1]为常量）即n= 2m，计算得到T[n]= 2(logn)T[1]+mn=nT[1]+nlogn。最后得出最优时间复杂度为O(nlogn)。最差的情况是基准元素pivot是序列中最大或最小的元素，这种情况就是冒泡排序了，时间复杂度为O(n2) 。正常的情况下基准元素pivot是待排序序列中的记录，快速排序的平均时间复杂度也是O(nlogn)。快速排序的空间复杂度比较复杂，主要为递归调用消耗的空间，最优情况即每次都平分的情况下为O(logn)，最差情况即退化为冒泡排序的情况下为O(n) 。排序算法的稳定性主要在排序比较过程中，关键字相同的两个元素之间是否发生交换。判断排序算法稳定性的方法很简单，即排序在相邻的两个元素之间进行，就不可能发生相同元素的交换，这个算法就是稳定的，如果是间隔的排序，就会发生交换，这个算法就是不稳定的。根据前面冒泡排序和快速排序的算法排序思想，可以判断冒泡排序的稳定性是稳定的，快速排序的稳定性是不稳定的。

综上分析冒泡排序及快速排序两种算法的时间复杂度、空间复杂度和稳定性比较如表1所示。

表1 算法的复杂度及稳定性

综上对冒泡排序和快速排序的分析，不难发现冒泡排序算法作为基本交换排序算法易懂，原理简单易学，成为很多初学排序人员的入门排序算法。但由于使用双重循环，时间复杂度较高，对于大数据量处理实用价值不大。快速排序作为冒泡排序的改进和优化，结合了分治与递归的思想，也极易理解，运行也比冒泡快，但它的不稳定性也带来一定的限制。

4 结束语

本文对交换排序中冒泡排序和快速排序进行了研究比较，阐述了两种排序算法的基本思想和执行过程，并对两种算法的时间复杂度、空间复杂度和稳定性做了比较，为程序开发者选择交换排序算法提供一定参考。在实际运用中，针对冒泡排序和快速排序两种排序算法的选择，要根据排序序列的具体情况具体分析，数据量增大时，快速排序比冒泡排序效率高出很多，如果数据规模较小，两者效率相差不大。