基于VAD的块稀疏自适应滤波切换算法

魏丹丹，李念念，毛海峰

（遵义师范学院 信息工程学院，贵州 遵义 563002)

0 引言

免提语音通信系统、音频会议系统和助听器等回声消除应用场景中，由于扬声器和麦克风耦合产生回波是一个亟须解决的问题[1]。自适应滤波器为此提供了很好的解决方案，方案包括算法和结构两方面。其中，自适应滤波算法主要用于更新滤波器权重系数，使滤波器可以在不断变化的外部环境中稳定工作[2-3]。基于NLMS 或LMS 的横向自适应滤波器具有均方误差小、计算成本低、实现简单、鲁棒性强等优点，成为最优选择。但由于语音信号具有高相关性和非稳态特点，算法收敛速度较慢。同时由于声波回波路径的时变性，需要通过不断更新自适应滤波器系数[4]来跟踪其变化。为了解决这一问题，文献[5-6]中提出了几种NLMS的改进方法。其中一类得到广泛应用的改进算法是稀疏类自适应滤波算法，该类充分利用声学回声路径的稀疏先验性来提高算法收敛速度。所谓稀疏先验性，是指滤波器权重系数大多数都是零或者较小的系数，很少有非零或大系数。根据非零系数的分布，常见系统有单一簇状稀疏系统或多簇稀疏系统[7-8]。

在对相关稀疏算法进一步研究的基础上，提出一种更具有工程实践意义的切换算法，该算法利用语音活动检测(VAD)技术引入一个阈值来区分输入语音信号是高电平还是低电平。利用快、慢包络计算边际的最大功率值作为阈值，构造一个稳定变量。将阈值与输入信号功率值进行比较后，算法在NLMS 和BSNLMS 之间进行切换。利用BS-NLMS 作为输入激励在高电平时增强收敛性，当NLMS 作为语音在低电平时增强收敛性。

1 AEC的实现及其算法

1.1 AEC 框架模型

声学回声消除(Acoustic Echo Cancellation，AEC)的系统框架结构如图1 所示[9]，远端语音信号x(n)经过声学回声路径w(n)产生回波信号d(n)，传递函数w(n)通过对远端语音信号x(n)滤波产生回声信号的复制信号y(n)。应用最广泛的是基于负梯度瞬时均方误差最陡下降方法的NLMS 算法，横向滤波器的权重矢量更新公式归纳如下：

图1 声学回声消除系统框架图

上述NLMS 算法中，x(n)Tx(n)是正则化因子，步长因子取值范围：0 ＜μ＜2，起着决定稳态误差和收敛速度的重要作用，抽头系数在时刻n的值：

M是滤波器长度。输出信号y(n)如下：

残余回声：

1.2 BS-NLMS算法

一般情况下，声学回波信道的脉冲响应只有少量非零系数，并且非零系数通常是以单簇或多簇的形式规律分布[10]，本文讨论的是典型具有稀疏特性的单聚类声学回声信道。此类声学回声信道的模拟可以采用块稀疏自适应滤波算法，算法在代价函数中插入额外的附加因子l(2,0)混合低阶范数改善算法稀疏性能，该混合范数利用其良好的约束性，使得算法的参数解尽可能靠近0而得到稀疏解，算法代价函数如下：

式中，低阶混合范数l(2.0)用来衡量信道块稀疏程度，参数λ是平衡附加因子和算法均方误差的正数。

其中，w[i]=[w(i-1)P+1,w(i-1)P+1,...,wiP]T是第i组权重系数矢量，N和P分别是抽头系数w(n)的分组数目以及分组长度。利用最陡下降算法更新权重系数矢量，得到如下利用稀疏先验特性的系数更新公式：

其中，g(w) =[g1(w),g2(w),...,gL(w)]T，而

α是一个正常数，μ是步长因子，主要用来保障稳态误差和收敛速度之间的平衡，κ=μλ/2 是用来调整更新公式对靠近0解的吸引力参数[11-12]。

1.3 VAD方案

根据文献12得到如图2所示，基于包络跟踪法跟踪输入激励的快、慢包络，以提高自适应滤波器的性能和控制自适应算法的更新。对于慢包络跟踪器，输入信号绝对值x(n)的一阶IIR平滑处理如下：

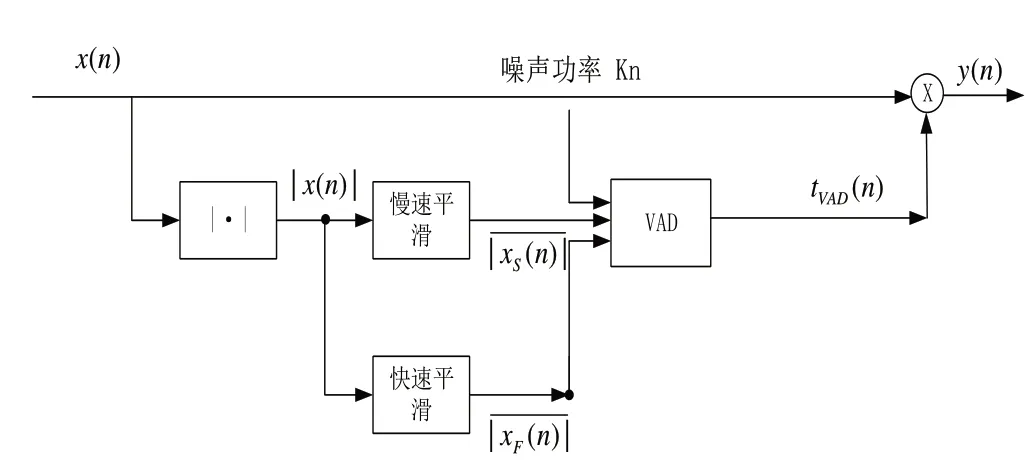
图2 VAD的快慢包络检测法

相似地，可以得到快包络：

VAD 的基本原理是:在活跃语音时段，快速包络跟踪器输出始终大于慢速包络跟踪器，当语音信号属于静默时段，慢速包络输出将超过快速包络输出。最终得到如下VAD的输出xD(n)：

2 基于VAD的自适应滤波切换算法

新算法的基本思想是采用开关机制对不同算法分别更新，通过VAD 方案在NLMS 和BS-NLMS 之间选择，算法的原则是根据输入信号的功率，方案如图3所示。利用BS-NLMS 和NLMS 算法在收敛性和均方误差方面不同的性能。通过VAD 输出得到用于能量比较的阈值，算法在输入能量大的时段使用BSNLMS 算法，在输入能量小的时段使用NLMS 算法,两种算法具有相同的滤波器结构。

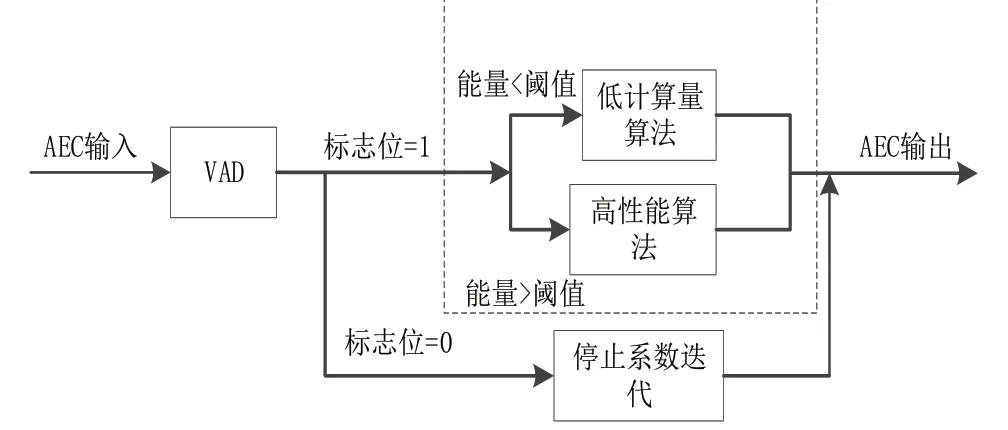
图3 改进算法的切换结构

在切换结构中，引入新变量Ts= max(xD(n))，它是VAD输出xD(n)的最大值，可以写成:

当输入信号P(n)的功率小于Ts时，采用NLMS 算法对系数进行自适应，得到较小的均方误差。当输入信号P(n)的功率大于Ts时，采用BS-NLMS算法对系数进行自适应，收敛速度较快。

递归方程可以写成：

其中，μ1,μ2是步长参数，γ是正则参数。考虑到算法的切换，计算复杂度不容易计算。因此，对于计算复杂度，只考虑每次迭代的乘法计算。设L为自适应滤波器长度，P是滤波器分组后的长度。该算法将输入信号建模为低M 阶自回归(Auto Regressive)过程进行自适应滤波。在文献[13]中，NLMS算法每次迭代需要2L次乘法来更新权值，对于BS-NLMS，需要2L+6次乘法，4L+ 6次加法，L P次除法。本文中，由于算法是在两个算法之间切换，所以改进的切换算法运算量在两个运算量之间。

3 仿真实验

对本文第2节中描述的改进切换算法进行了仿真实验，验证了其对语音输入的性能，AEC实验进行如下。在本次实验中，麦克风放置在离扬声器0.45 m的地方，分别对回波信号和高斯噪声进行采集。图4所示为远端语音在普通办公室中扬声器播放的信号能量估计。近端语音是零均值高斯白噪声的系统噪声。图5是该仿真条件下的真实房间脉冲响应和算法估计的房间脉冲响应。在算法估计中，参数可以选择以下常数:

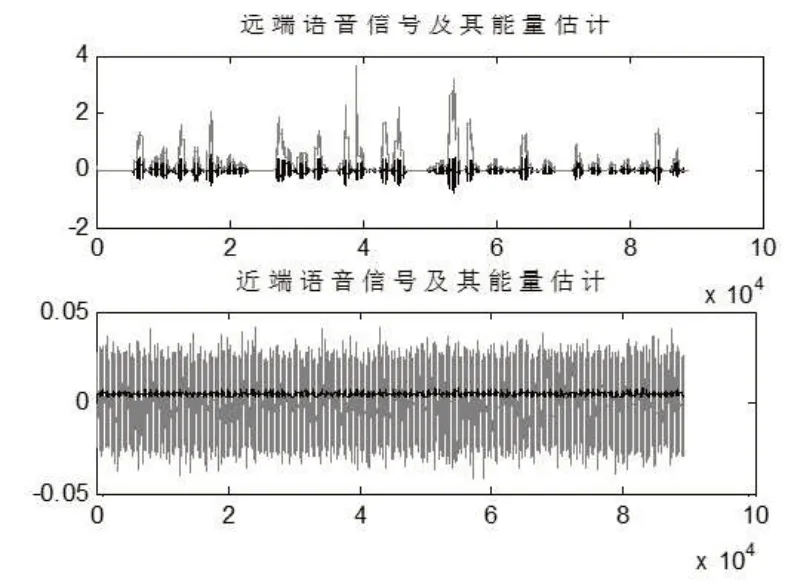
图4 远端及近端语音信号和能量估计

图5 房间脉冲响应及其估计

快速包络|uF(n) |为上曲线，慢速包络|uS(n) |为下曲线。结果绘制如图6 所示。可以看出，图6 中的阈值Ts是uD(n)的最大值。图7 显示了使用NLMS 和本文算法的AEC输出。实验结果表明，该方法具有较好的回波抑制效果。值得注意的是，该算法的性能得到了提高，特别是回波峰值明显降低。

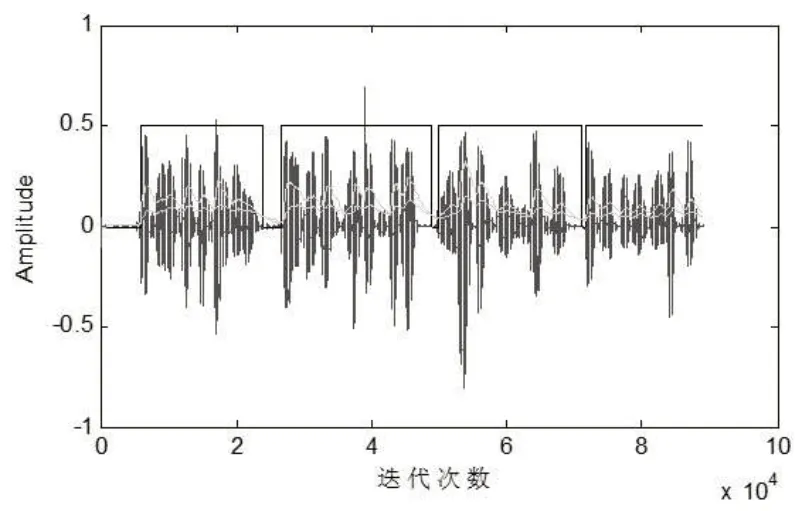
图6 语音的VAD估计及快慢包络

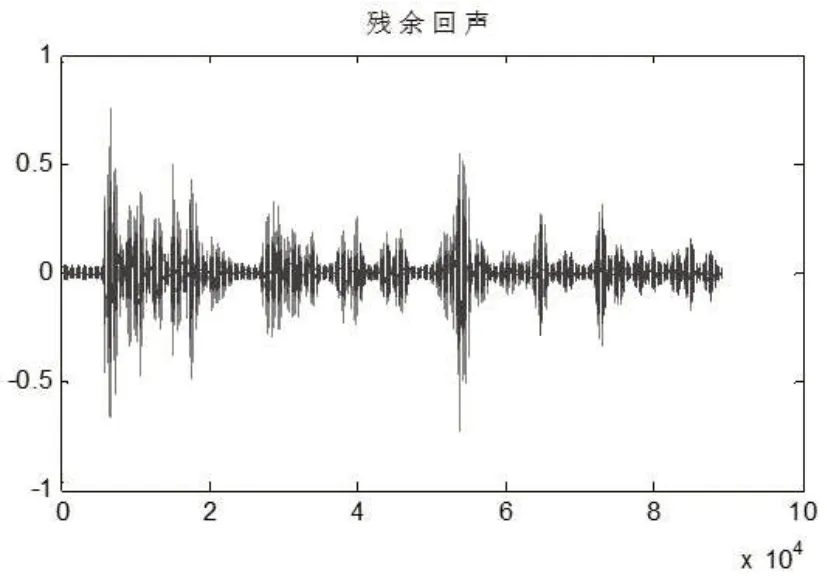
图7 残余回声对比

4 结论

本文提出的方案结合了两种不同算法的优点。通过快、慢包络的能量计算得到阈值,通过阈值和输入语音信号能量的比较，得出切换点。结果表明，该方法有明显的回波抑制效果。此外，它实现了一个相对合适的计算复杂度。