新型线驱动双关节连续体机器人分析、设计与试验
赵晨鑫, 姜振华, 胡 俊*,
(1.东华大学 机械工程学院,上海 201620,E-mail:hjmorning@hotmail.com;2.东华大学 人工智能研究院,上海 201620)
介入手术是在影像设备的引导下,将特制导管、器械引入人体进行诊断治疗的一种现代化微创治疗方式。相比于传统的介入手术,利用机器人系统辅助进行介入手术可以提高手术的精准性、降低医务人员的工作强度[1]。由于连续体机器人凭借较小的整体结构即可实现灵活的弯曲运动,被广泛研究并应用于介入手术中[2]。
连续体机器人属于一种新型的仿生机器人[3],它的结构类似于蛇的身体、猴子的尾巴、海星的触手等[4],灵活度高且形状多样,可以更好的适应复杂的环境。哈佛大学Bergeles等[5]设计了一种结构由需求所定的新型的同心管连续体机器人,根据工作路径来对连续体的整体结构进行分析设计,但存在应用场景较为局限、控制精准性低等不足。意大利Calisti等[6]根据对章鱼触手的组织结构进行仿生,研制出了一种硅胶成型的丝驱动的连续体机器人,通过协调驱动实现弯曲运动,整体刚度太小、控制性差。Li等[7]根据仿生原理设计了一种线驱动柔性机构(CWFM),其弯曲长度及曲率可控,提高了机器人的工作空间及灵活性,但机构的制造困难、运动求解较为复杂。
由于连续体设计的各异性,其驱动方式也不同,常见的驱动形式主要分为气动[8-12]、线驱动[13-16]、磁力驱动[17-19]。针对材料、结构、驱动方式等不同,其运动学模型建立的方法也较多,对于不同的连续体机器人可应用不同的分析方法,Walker等[20]基于恒定曲率假设,通过对一种仿象鼻连续型机器人进行分析,提出了一种改进D-H法对连续体机器人进行了运动学建模与分析。Chen等[21]提出了一种用于解决单关节气动连续体机器人运动的独特运动控制算法。Chikhaoui、Trivedi、Mahvash等[22-24]研究人员通过采用cosserat连续体介质力学理论对连续体机器人的物理模型及运动学进行了分析,在肌腱驱动、同心管型连续体机器人中具有较好的应用,但整体求解较为复杂,求解效率较低。
本文根据连续体机器人的仿生原理设计了一种线驱动的新型介入手术机器人。基于分段常曲率假设,建立连续体机器人运动学模型,采用一种简便的数学分析法对运动学进行分析计算,并对双关节之间运动的耦合进行了解耦分析。最后,搭建机器人样机平台进行试验,建立补偿控制模型,提高了系统控制的精准性。
1 连续体机器人结构与控制系统设计
针对微创介入手术实际需求,本文设计了连续体机器人的运动本体以及相应的运动控制系统,以实现一定工作范围内的弯曲和旋转。
1.1 连续体机器人结构
连续体机器人的柔性臂结构如图1所示,主要由两个关节组成,其中第一关节具有一个自由度,第二关节具有两个自由度,外壁固定有供驱动线通过的微小径空心管,根据机器人的运动需求均匀分布在主体的外部。驱动线由电机控制其拉紧与释放,用于实现连续体的运动。整体的体积小、功能合理,采用线驱动灵活性好、运动可靠。

▲图1 连续体柔性臂结构图
如图2所示,连续体机器人的整体结构包括电机、传动装置、卷绕盘等,驱动线穿过固定装置后与卷绕盘连接,由PC机发送控制信号控制卷绕盘的旋转,带动驱动线的伸缩变化,从而实现连续体机械人柔性臂的弯曲、旋转运动。控制电机的旋转来实现连续体姿态的控制用于适应不同环境。

▲图2 机器人整体结构设计
1.2 运动控制系统设计
如图3所示,控制系统部分主要包括PC机、控制模块、驱动模块以及机器人运动组件。PC机主要用于对机器人的主动操作控制以及状态检测,发送控制指令给控制模块,控制模块收到指令后通过内部逻辑计算将控制指令转化为控制信号传给驱动模块,最终转化为驱动信号传给运动组件,实现机器人整体的运动。
同时,处理后的机器人状态信息将最终反馈给PC机进行呈现,达到状态的实时性检测。其中,在信号处理部分,PC机与控制模块之间通过ADS实现彼此的信号的交换,控制模块与驱动模块之间则是通过EtherCAT实现数值化通讯,具有稳定性好、响应速度快等特性。

▲图3 控制系统框架图
2 双关节运动学分析
双关节连续体机器人的运动学可以通过驱动空间、连续体空间、操作空间之间的映射关系进行描述。其相互关系如图4所示。

▲图4 连续体机器人空间描述图
其中,驱动空间由驱动线长度li(i=1,2,a,b,c,d) 所决定,连续体空间由关节参数(θ1、θ2、φ2)所决定,θ1为第一关节的弯曲角度,θ2、φ2为第二关节的弯曲、旋转角度。与关节型机器人不同,无法采用传统的机器人运动学分析法进行分析,则本文基于分段常曲率假设,对连续体机器人进行建模,且采用一种更为简单、直观的数学图解法进行连续体的运动学分析。
2.1 双关节运动学模型构建
如图5所示,连续体在空间中的任意位置可通过弯曲和旋转两种变化来实现,其中θ为连续体的弯曲角度,φ为连续体的旋转角度。

▲图5 连续体运动模型
由此,双关节连续体机器人的运动学模型如图6所示,其中,l1、l2为控制第一关节运动的两根驱动线的长度,la、lb、lc、ld为控制第二关节运动的四根驱动线的长度。O0为第一关节底部中心位置,O1为第一关节末端中心点,O2则为第二关节底部中心点。其中,x0指向l1驱动线通道的方向,z0垂直于连续体底面向下。

▲图6 双关节连续体几何模型
2.2 连续体空间与操作空间的映射分析

▲图7 第一关节连续体轴向剖视图
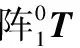
得到第一关节的齐次变换矩阵:
(1)
式中:l1第一关节的长度,c代表cos ,s代表sin 。Pz0(l1,θ1),Ry0(θ1),Pz1(l1,θ1)分别表示绕z0的平移变换矩阵、绕y0的旋转变换矩阵、绕z1的平移变换矩阵。

▲图8 第二关节连续体轴向剖视图
(2)
式中:l2为第一关节的长度,R表示旋转矩阵,P表示位置向量。
由式(1)、(2)可得,此双关节连续体机器人基坐标系至末端坐标系的齐次坐标变换
(3)
式中:
对于操作空间至连续体空间的空间映射关系,其求解与传统串联机器人的逆运动学求解类似,为非线性方程组的求解,难以得出解析解,考虑机器人空间轨迹的连续性,故可以使用牛顿—拉夫森迭代方法对方程的数值解进行求解,根据机器人末端姿态,计算出关节角变动量并进行迭代,最终收敛至目标值,得到机器人对应的关节运动角度。
2.3 驱动空间与连续体空间的映射分析
连续体机器人柔性臂采用六线驱动方式,走线方式如图6所示,第一关节采用双线驱动进行弯曲变形,第二关节采用四线驱动,可产生弯曲和旋转两种变化状态,其空间映射关系如图9所示。其中,1,2为第一关节的两根驱动线所在通道孔,a,b,c,d为第二关节的驱动线,φi(i=a,b,c,d)为旋转角度与拉孔与连续体中心连线的夹角,m为拉线孔至连续体中心的距离。

▲图9 驱动空间与连续体空间的映射
根据图6及图9所示的映射关系可以推导出当第一关节弯曲θ1角度后驱动线的变化量:
(4)
式中:Δl1、Δl2即为第一关节1处、2处驱动线的线长变化量,r、r1、r2分别为弯曲时连续体中心线、1处驱动线、2处驱动线的曲率半径。
对于第二关节须同时考虑自身姿态变化与第一关节产生的耦合变化:
① 考虑第一关节的弯曲对第二关节的耦合运动影响:
(5)
② 考虑第二关节自身弯曲θ2、旋转φ2角度后:
(6)
式中:Δli1、Δli12(i=a,b,c,d)分别为第二关节a、b、c、d处驱动线因耦合运动和自身运动而产生的线长变化量,ri1、ri1(i=a,b,c,d)分别为连续体第二关节耦合运动、自身运动下a、b、c、d处驱动线的曲率半径。
第二关节的实际变化量为自身运动量加上第一关节对其的耦合运动量,由式(5)、(6)可得第二关节驱动线的变化量为:
(7)
式中:Δli(i=a,b,c,d)分别为第二关节产生运动时a、b、c、d处驱动线的实际线长变化量。
式(7)即是连续体空间至驱动空间的映射关系求解结果。联立式(4)~(7)即可得到机器人驱动空间至连续体空间的映射关系:
(8)
驱动空间与连续体空间的映射的分析计算结果即反映了机器人弯曲旋转变化运动角度与线长变化的关系,对机器人姿态控制具有重要意义。
3 运动学仿真研究分析
机器人的操作空间反映了机器人可活动范围的大小,通过所求得的齐次变换矩阵T,可以得到末端参考点的坐标表达式。采用用于随机现象描绘的蒙特卡洛法,在双关节连续体的弯曲和旋转范围内随机取点,绘制出每个末端点位置,即可得到机器人的操作空间Ω。设定机器人在初始时处于直立状态,第一关节中心点为坐标系原点,在此取机器人连续体的参数l1=100 mm,l2=45 mm,θ1∈[-2π/3,2π/3],θ2∈[0,π/4],φ2∈[0,2π],中心距m=4.2 mm,其中,连续体的长度设计可满足机器人运动需求,在运动范围内随机取50 000点,使用Matlab绘制得到的双关节连续体机器人的运动空间如图10(a)~图10(d)。
如图11的(a)、(b)图所示,根据驱动空间至连续体空间的运动分析计算,取各关节运动范围内连续变化的100个采样点进行仿真,即可对机器人末端点在工作空间中位置变化与驱动线长度变化之间的关系进行更直观的展现。
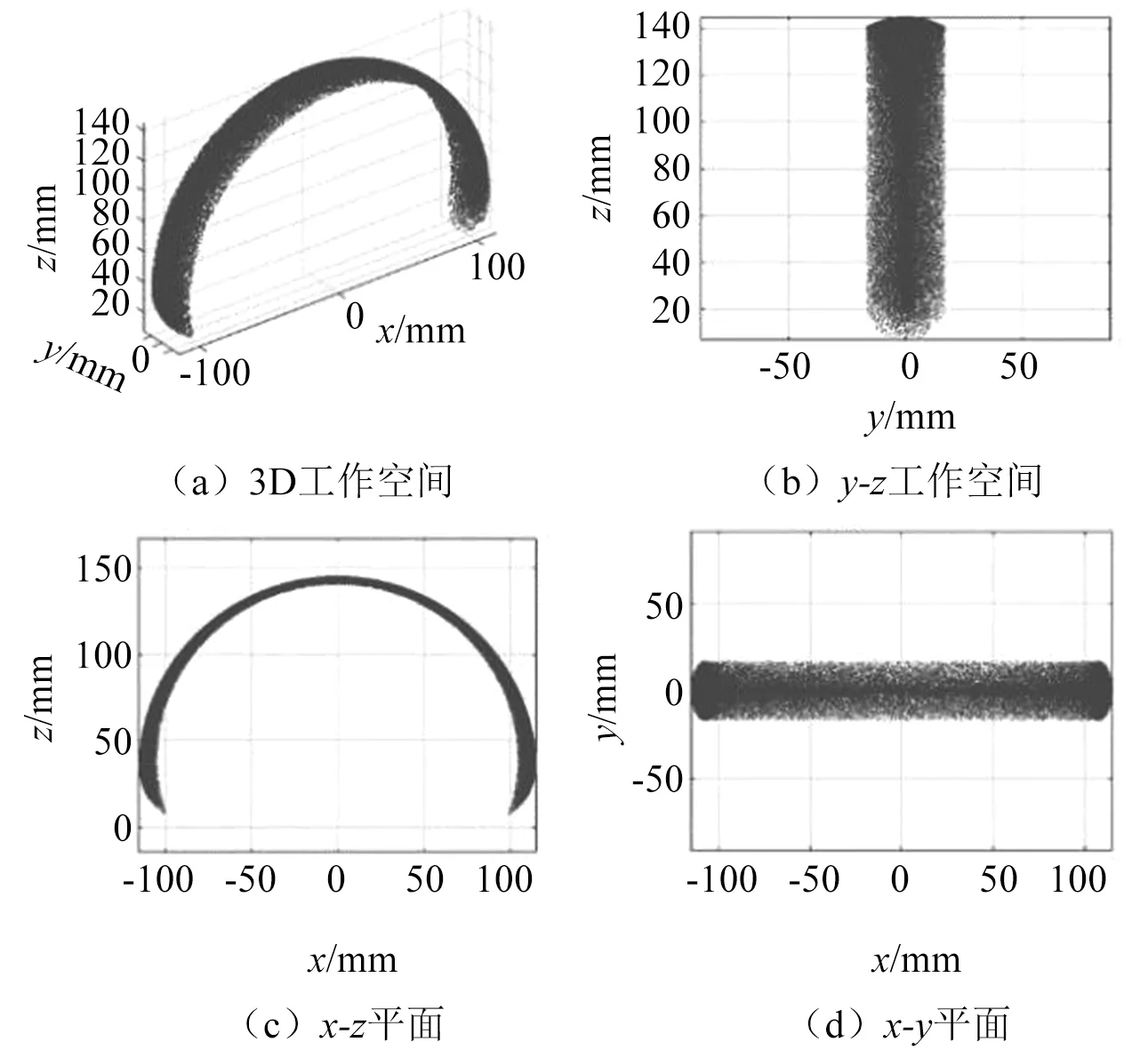
▲图10 机器人工作空间仿真图

▲图11 机器人末端点与驱动线长度变化关系仿真
4 连续体机器人试验与结果分析
为进一步验证双关节连续体运动学分析方法的有效性及连续体机器人的实际行为能力,搭建如图12的试验系统。
该系统主要由机械人机构本体、控制系统组成。控制系统中采用EtherCAT总线,TwinCAT、Qt软件系统,驱动模块采用TECHSOFT伺服驱动,电机采用ECU22048系列直流无刷无齿槽电机,具有小尺寸、大力矩、高转速等优点。PC机上实现对机器人的操作以及机器人状态的显示。连续体机器人柔性臂的材料为镍钛合金,总长度为145 mm,其中第一关节长度为100 mm,第二关节长度为45 mm,主体部分直径为8 mm,外壁部分的驱动线通道空心管直径为0.4 mm,驱动线采用高性能的合金丝,其强度符合机器人运动需求,外部使用硅胶外壳进行包裹,起保护作用,增加稳定性,卷绕盘由光固化打印制作而成。

▲图12 连续体机器人试验样机平台
为更好的测试连续体机器人的弯曲行为能力,如图13所示,在各关节运动角度范围内,分别对机器人进行初步的运动试验。

▲图13 连续体机器人弯曲试验
由试验结果可知,所设计的双关节连续体机器人可以实现所预期的弯曲、旋转运动,验证了运动学分析方法的有效性以及控制方法的可行性。
但由初步试验可知,机器人运动的准确性相对较差,这是由于所设计的机器人是一个多因素耦合的系统,其行为能力受到多重因素的影响,包括机器人整体的刚度、材料本身的性能、加工精度和驱动线的预紧力,刚度以及材料性能的不足使得机器人运动过程中无法始终保持常曲率状态,预紧力的不足则会导致运动过程中驱动线的松弛,均会对运动的精准性造成较大影响。多重因素的影响下的实际角度值与理论值将存在误差,在各关节的弯曲运动中表现得更加明显。

▲图14 补偿控制模型
如图14所示。
原有模型在理论角度的基础上直接进行运动学映射,对驱动线的变化量进行求解,根据求解结果驱动电机进行相对应的运动来操纵机器人运动,存在较大运动误差。为减小误差,引入补偿函数对理论角度值进行补偿处理,将补偿后的角度传入后续控制过程则可以达到对机器人运动的补偿控制,减小机器人实际运动角度与理论角度之间的误差,提高系统控制的精准性。
在其他连续体机器人运动补偿控制方法中,常采用通过影像设备对机器人进行实时检测和运动补偿的方法。此方法下,控制的准确度将高度依赖于实时位置检测的准确性,增加了系统的复杂度、降低了机器人的自动化程度且复杂了机器人操作,不能很好的适用于所设计的小型机器人系统。与之相比,通过实际运动求解补偿函数,建立补偿模型的方法对于所设计的机器人系统具有更好的应用性,影响机器人运动输出的因素将只有理论角度这一个因素,既减小了求解的复杂度与机器人操作难度,又保证了运动控制的精准性。
在此,具体实施方法为:依据试验输入的理论角度值,利用常曲率模型下机器人运动学映射关系求解出六根驱动线的变化量,驱动卷绕电机运行相对应的角度值来控制机器人的姿态变化,并对机器人的姿态进行测量记录。将测量所得的实际角度值设置为输入x,理论角度值设置为输出y,通过MATLAB中的cftool对(x,y)的散点图进行拟合,对于多种拟合方式下的拟合结果,选择最佳拟合函数即为我们所求的补偿函数,建立补偿模型,将理论角度转化为补偿后的角度值传入后续控制过程,实现对控制系统的运动补偿。
通过多次试验测量及多种拟合方式的对比得到最佳拟合为:
(9)
式中:(x1,y1)为对第一关节弯曲角度θ1的拟合方程,(x2,y2)为对第一关节弯曲角度θ2的拟合方程,(x3,y3)为对第一关节弯曲角度φ2的拟合方程。
均方根误差RMSE1=1.21,可决系数R-square1=0.999,RMSE2=0.1667,可决系数R-square2=0.999,RMSE3=4.423 8,可决系数R-square3=0.998,。拟合优度好,可以达到预期效果。补偿模型建立的结果同步反应了补偿控制前机器人运动时的弯曲角度所产生的误差较大,而旋转角度产生的误差较小。
为进一步检验补偿后控制系统的准确性,在各关节运动角度范围内,开展了连续体机器人姿态误差试验。在试验中,取各关节运动范围内连续变化的30个采样点,对机器人进行补偿控制和未进行补偿控制的实际姿态进行测量。对结果进行统计,绘制如图15所示的试验结果图,其中(a)、(b)、(c)分别为第一关节弯曲角度θ1、第二关节弯曲角度θ2、第二关节旋转角度φ2的试验结果图。
如表1中统计的试验结果数据可知,试验中机器人第一关节的弯曲角度最大平均绝对误差为5.48°,最大误差为-7.5°;第二关节的弯曲角度最大平均绝对误差为1.23°,最大误差为-2.60°;旋转角度最大平均绝对误差为2.11°,最大误差为-3.50°,最大误差分别占各自全运动范围的3.125%、5.778%、0.972%。经过分析,补偿后的控制仍产生有误差的原因为:试验中连续体本身反复弯曲运动后无法完全恢复至初始状态,拉线无法在任意时刻处于完全绷紧状态且存在测量误差。但补偿后的系统误差已在可接受范围内,可满足实际需求。
5 结论
本文针对自主设计的新型线驱动双关节连续体机器人,提出并验证了一种运动学分析及补偿控制方法。基于分段常曲率假设,建立了双关节运动学模型。在考虑两关节耦合效应的情况下对双关节连续体部分进行了运动学分析,通过MATLAB仿真验证了机器人的工作空间以及末端位置变化与线长变化之间的关系。基于双关节连续体机器人样机上的试验结果,分析了机器人运动误差产生的原因,建立了机器人补偿控制模型,补偿后的运动精度可满足实际使用需求。

