基于经验模式分解和多项式拟合的静止卫星变轨预测

李 烨，石会鹏，张 周，上官泽胤

（1.31007 部队，北京 100079；2.北京东方波泰无线电频谱技术研究所有限公司，北京 100041；3.军事科学院，北京 100071）

空间频率轨道资源按照先登先占原则申请使用[1]。为维护我国空间频率轨道资源安全、拓展空间频率轨道资源利益，掌握全球静止卫星的轨位数据成为关键[2-3]。受姿态控制、摄动力等因素影响，实际运行中静止卫星的轨位具有小幅波动[4]。从具有波动的经度信号等轨道参数中，及时、准确识别并预测静止卫星变轨，仍面临缺少自动化、高鲁棒性算法的困难[5]。

常用的噪声滤除方法[6-9]为使用小波变换在不同尺度上分解带噪信号，再在不含噪尺度上对信号进行分析，但其性能受小波基选取影响。经验模式分解方法[10]可根据信号本身的时间尺度特性自适应选取“基函数”，克服了小波基选择难题。

该文在经验模式分解域，通过残差分量多项式预测值与真实值误差的阈值化处理，实时判断静止卫星是否变轨。

1 EMD方法和一致性EMD方法

经验模式分解（Empirical Mode Decomposition，EMD）方法能够根据信号本身的特性，自适应地将时域信号分解为一组不同尺度的固有模态函数（Intrinsic Mode Function，IMF），而每个尺度上分解所得残差分量代表原始信号的趋势或均值。

设x(i)为待分解的原始信号，i=1,…,I；cn(i)为第n次分解得到的IMF 分量；rn(i)为第n次分解得到的残差分量，n=1，…,N。EMD 算法将原始信号x(i)分解为N个IMF 分量c1(i)、c2(i)、…、cN(i)和一个残差分量rN(i)的和。其中，N个IMF 分量分别包含了原信号x(i)中不同时间特征尺度大小的成分，且各IMF分量的时间特征尺度随n增加而依次变大，这说明EMD 方法具有尺度滤波特性。

在边缘提取算法中，一般选择暗区域或噪声信号在某个尺度上信号的特征量作为该尺度上检测阈值。但是，如果分别对待分析信号和噪声进行经验模式分解，由于EMD 方法是自适应基函数分解方法，且两信号的尺度特性不同，那么就不能保证两个信号的第n阶IMF 分量在同一尺度上，也就不能使用噪声信号第n阶IMF 或残差分量的特征量作为该尺度上边缘检测的自动化判决阈值。文献[11]利用EMD 方法中计算上、下包络线的内插操作仅与拟合点邻近有限个极值点（例如三次样条曲线内插需要临近5 个极大值点或5 个极小值点）有关的特点，通过保证参考噪声各阶IMF 分量的筛分次数与原始信号x(i)各阶IMF 分量的筛分次数相同的方法，来估计各阶rn(i)中噪声信号。这种对参考噪声的分解方法既保证了信号x(i)与参考噪声分解得到的IMF 分量数相同，又保证了两个信号的第n阶IMF 分量在同一个尺度上，即保证了两者的一致性，因此称其为一致性经验模式分解（consistent EMD）方法。

2 该文变轨预测算法实施步骤

经验模式分解和多项式拟合的静止卫星变轨预测算法的基本思想是利用EMD 方法的多尺度滤波特性[12-14]，对卫星经度信号在多个尺度上进行平滑滤波，并对滤波后的信号进行多项式拟合、预测，最终通过预测误差判断卫星是否变轨。

2.1 经度信号预处理

在静止轨道卫星发射阶段，其经度信号会产生大幅度变化。这种剧烈变化会导致多项式拟合误差增大，影响静止卫星变轨判断算法的准确度。图1（a）显示了某静止卫星的历史经度信号。图中卫星发射阶段经度信号、运行周期信号同步变化，且变化幅度远大于其进入静止轨道后正常变轨时变化幅度。如果单一采用静止卫星经度信号进行变轨预测，会造成将发射阶段的经度变化误检测为正常变轨情况。

图1 卫星经度信号预处理效果

为了消除静止轨道卫星发射阶段对变轨预测算法影响，该文采用卫星运行周期信号作为参考信号，以运行周期大于23 小时56 分为判断依据，在变轨预测前对原始经度信号进行预处理，将静止卫星发射阶段的经度信号从原始经度信号中删除。图1（c）显示了某静止卫星经度信号预处理的结果。

2.2 预处理后经度信号经验模式分解

经验模式分解方法得到的各阶IMF 分量cn(i)包含了待分解信号x(i)或rn-1(i)中高频成分，rn(i)则包含了x(i)或rn-1(i)中低频成分，因此rn(i)可看作原始信号x(i)经不同平滑滤波器输出的、在不同尺度上的数据。阶数n越小则rn(i)就越接近原始信号x(i)，所含噪声成分越多，变轨预测算法受噪声影响越大；阶数n越大则rn(i)就越平滑，所含噪声成分越少，变轨预测算法受噪声影响越小；同时，阶数n过大、rn(i)过分平滑会导致rn(i)丢失细节而导致变轨预测结果错误，因此合理选择后续拟合分析信号rn(i)的阶数n，直接影响最终变轨预测准确性。该文选取第1 尺度上的残差分量r1(i)作为拟合分析信号。同时，由于该算法是预测算法，经验模式分解、多项式拟合预测等全部操作均基于1 到i-1 时刻的历史数值，因此每当获取到新的x(i)值后，需对x(1:i)进行经验模式分解，得到r1(i)；r1(i)并非由x(i)一次经验模式分解计算得出。

图2 显示了对某静止卫星的预处理后经度信号采用EMD 方法进行多尺度分解的例子。其中，原始信号x(i)采用EMD 方法分解得到5 个IMF 分量以及r1(i)至r5(i)共5 个残差分量。

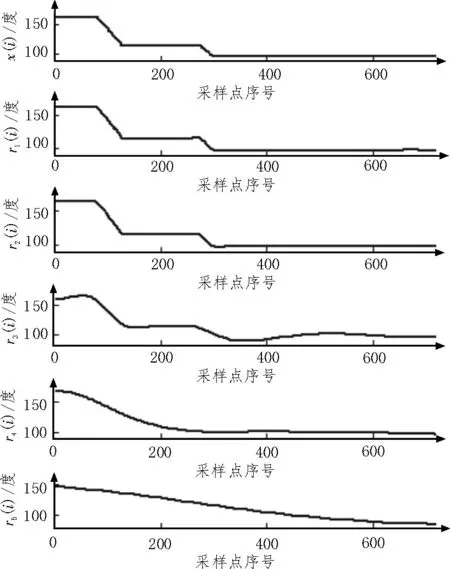
图2 预处理后经度信号的分解结果

2.3 多项式拟合与预测

为了实时检测静止卫星变轨，该文采用对比某时刻某尺度上残差分量预测值与真实值方法实现。其中，预测值由某时刻i+1 之前的历史残差分量数据，采用滑动均值法求得。参考文献[15]引述，该文选用0 阶多项式对第一尺度上残差分量r1(i) 中第i-7、i-6、i-5、i-4、i-3、i-2、i-1、i共8 个时刻的数值进行拟合，并采用该0 阶多项式预测第i+1时刻的残差分量数值re1(i+1)，即：

与文献[15]引述方法不同，为了实现实时预测静止卫星变轨，该文的多项式拟合只使用了后置多项式拟合，避免了前置多项式拟合对某时刻i+1 之后未来数据的依赖。

2.4 噪声阈值估计与变轨判决

噪声幅度门限Tj的选取决定阈值化处理的效果，直接影响变轨预测算法自动化判决准确性。如果噪声幅度门限Tj取值较小，那么无法去除小幅机动造成的噪声影响，提高了变轨预测算法虚警率；如果噪声幅度门限Tj取值较大，那么将滤除掉部分变轨事件造成的小幅预测误差，提高了变轨预测算法漏警率。参考文献[16-17]所述，小波域滤波选取图像信号中“暗”区域的信号作为参考噪声,并通过对参考噪声进行小波变换求得各尺度上噪声阈值。但由于EMD 是一种自适应基函数滤波方法,单独对参考噪声直接采用EMD 方法分解既不能保证原始信号x(i)与参考噪声分解得到的分量数量相同,又不能保证原始信号x(i)和参考噪声的第n阶分量在同一尺度上。因此该文EMD 域变轨判决的噪声阈值选取方法不能简单借鉴小波域滤波。该文首先选取静止卫星在某轨位驻留期间的、平稳的经度信号作为参考噪声源信号，并对其去均值处理得到参考噪声信号；然后采用一致性经验模式分解方法对参考噪声进行分解，得到各尺度上参考噪声信号,从而计算出各尺度上参考噪声信号的功率；最后参考噪声功率的平方根即为该尺度上噪声幅度门限Tj。

判决静止卫星当前是否正在进行变轨的判据：如果第i+1 时刻的残差分量预测值re1(i+1)与第i+1时刻的残差分量真实值r1(i+1)的差值绝对值不大于第1 尺度上噪声幅度门限Tj，则判断在第i+1 时刻卫星未实施变轨；如果第i+1 时刻的残差分量预测值re1(i+1)与第i+1 时刻的残差分量真实值r1(i+1)的差值绝对值大于第1 尺度上噪声幅度门限Tj，则判断在第i+1 时刻卫星可能正在实施变轨。

3 实验结果与分析

该文使用Matlab 软件评估经验模式分解和多项式拟合的静止卫星变轨预测算法。其中，EMD 方法的筛选门限SD 取0.2；图1（a）所示静止卫星的经度信号作为待分析信号；图1（c）所示预处理后经度信号x(i)的两个变轨事件分别发生在第81-125、277-297 点之间。

图3 给出了预处理后经度信号x(i)采用经验模式分解和多项式拟合的静止卫星变轨预测算法预测变轨的例子。其中，图3（a）显示的是静止卫星在第81 个时间点开始变轨的预测结果，图3（b）显示的是静止卫星在第277 个时间点开始变轨的预测结果。图中，星号曲线表示第1 尺度上的残差分量实际值（曲线中9 个点取值均由预处理后经度信号x(1∶81)或x(1∶277)采用EMD 方法计算得出），空心圆曲线表示第1 尺度上的残差分量预测值（曲线中前8 个点取值由预处理后经度信号x(1∶80)或x(1∶276)采用EMD方法计算得出，第9 个点取值由前8 个点的值拟合预测得出，即re1(81)或re1(277)），实心圆曲线表示第1 尺度上的变轨判决门限（曲线中9 个点取值均由re1(81)或re1(277)减去噪声幅度门限Tj得出）。由图可见，在第81、227 这两个采样点，第1 尺度上的残差分量实际值超过了变轨判决门限，该算法对静止轨道卫星变轨事件实现了准确、及时预测。

图3 该文算法的变轨预测结果

为了对比该文变轨预测算法与文献[15]引述直接对预处理后经度信号x(i)进行多项式拟合预测的算法，实验进一步采用相同的参考噪声和上述两种算法，对预处理后经度信号x(i)第273 点的轨位小幅变化进行效果分析，结果如图4 所示（图中各曲线代表的内容同图3）。其中，图4（a）所示为采用该文变轨预测算法的预测结果；图4（b）所示为直接采用多项式拟合预测算法的预测结果。由图可见，该文所述变轨预测算法未在第273 点预测变轨；直接多项式拟合预测算法则出现变轨误判，产生虚警。该文所述变轨预测算法未出现虚警的原因应为EMD 算法消除了小幅轨位变化对多项式拟合预测的影响。

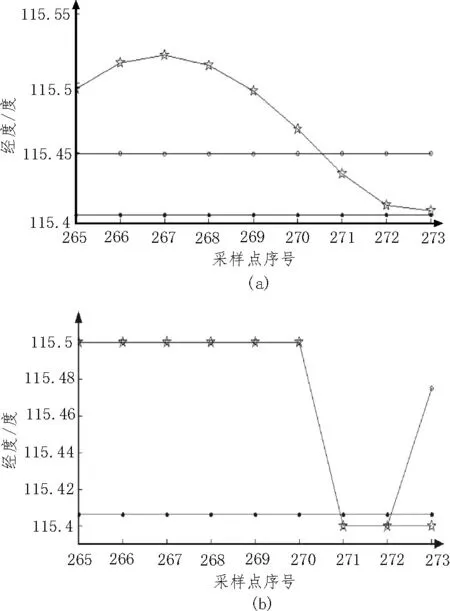
图4 轨位小幅变化的预测结果比对

4 结束语

该文提出一种经验模式分解和多项式拟合的静止卫星变轨预测算法。该算法基于EMD 方法的多尺度滤波特性，将残差信号的多项式预测误差与噪声阈值对比，实现从卫星经度信号中预测卫星变轨事件。以实际静止卫星为例的实验表明，该算法能够有效对静止卫星变轨进行实时预测，为实现变轨事件的自动预测指明了方向。