电容电流反馈并网逆变器闭环系统参数选择及稳定性分析
崔云晓
(中国信息通信研究院,北京100080)
0 引 言
随着中国产业结构、能源结构的调整,太阳能、风能等新能源并网比例显著提高[1],可再生能源分布式发电系统通常采用并网逆变器作为实现能源并入电网的接口,而并网逆变器运行稳定性问题一直没能得到很好的解决[2]。在实际工程中,并网逆变器的抗干扰能力一直不强,严重制约了可再生能源的广泛并网,因此,确定并网逆变器参数,分析并网逆变器运行稳定性具有十分重要的工程指导意义[1]。
对于并网逆变器运行稳定性问题,文献[3-4]对无源阻尼LCL型并网逆变器的控制策略进行了分析,通过电感串联电阻或电容并联电阻,达到抑制谐振尖峰的目的,但该方法能量消耗较大[5]。文献[6]提出了电容电流反馈的等效阻尼控制策略,通过电容电流反馈,实现与无源阻尼控制策略相同的控制效果,但该策略计算复杂,且没有给出明确的系统参数计算方法[7]。
该文在建立LCL型并网逆变器数学模型的基础上,分析PI调节器参数对系统环路的影响,根据系统环路约束条件,对电容电流反馈并网逆变器各参数进行分析确定,并通过Matlab对该系统进行仿真验证。
1 典型并网逆变器数学模型

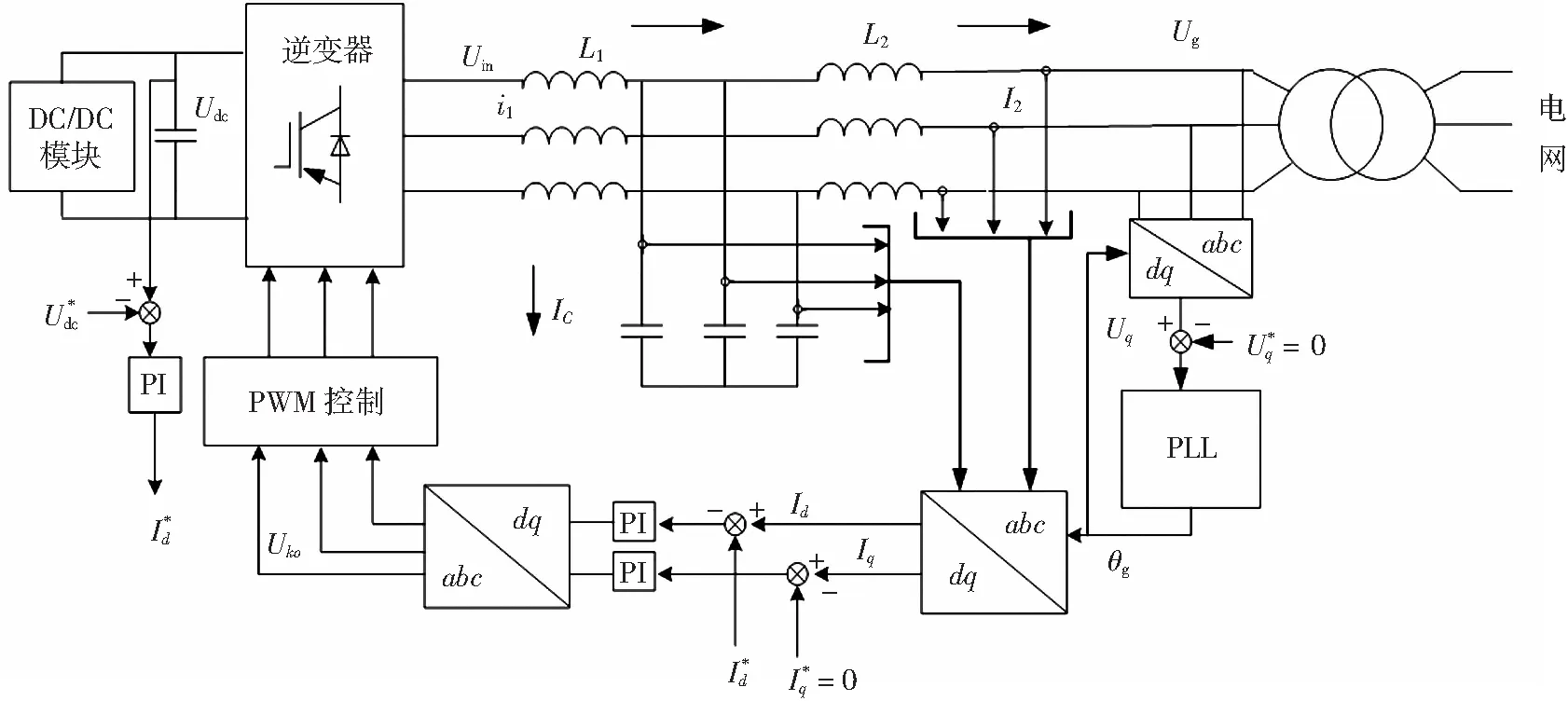
图1 LCL型并网逆变器系统控制结构框图

(1)

图1中电容电流与并网电流双反馈的控制方式,其控制框图如图2所示。其中,G1(s)=1/(sL1),G2(s)=1/(sC),G3(s)=1/(sL2)。G1(s)为电流调节器传递函数,s为ejw,H2为并网电流反馈系数,Uko为调制波信号,KPWM=Vm/Vtri为调制波到逆变桥输出电压Uin的传递函数,这里Vm为输入载波电压幅值,Vtri为三角载波幅值。

图2 LCL型并网逆变器电容电流反馈系统框图
2 系统环路增益及其频率特性
图2给出了基于电容电流反馈的有源阻尼控制框图,为得到该控制策略下的传递函数,需要对图2所示的控制框图进行等效变换。首先,令电容电流反馈系数H1=L1/KPWMCR,然后调整相应的结构框图,可以得到如图3所示的控制框图。

图3 LCL型并网逆变器电容电流反馈阻尼等效变换
其中
(2)
(3)
根据图3,可以得到环路增益表达式为
(4)
根据式(4),当Gi(s)=1时,其环路增益表达式的波特图如图4所示。其中,f0为基波频率,fc为环路增益截止频率,fr为LCL滤波器谐振频率。从图4可以看出,电容电流反馈有源阻尼控制可以有效抑制谐振尖峰,而对低频带与高频带的幅频特性影响很小。但这种阻尼方法对系统的相频特性影响却很显著,在低频段,系统相位就从-90°开始下降,在谐振频率fr处穿越-180°,然后逐渐降低至-270°。
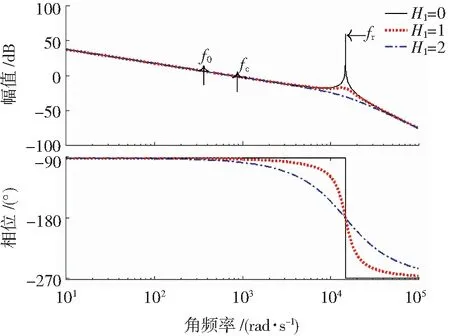
图4 电容电流反馈有源阻尼控制波特图
当电容电流反馈系数H1逐渐增大时,谐振频率处的系统环路增益幅值逐渐降低,相频特性曲线变得更加平缓。这说明,随H1的增大,其阻尼效果越高,但其稳定裕度却略有降低。需要注意的是,系统环路增益在谐振频率fr处穿越-180°,为了保证足够的相位裕度,截止频率fc需要低于fr。
3 PI调节器对系统环路的影响
当Gi(s)为PI调节器时,需要考虑PI调节器对系统稳定性能的影响。根据PI调节器的传递函数Gi(s)=KP+KI/s,可以得出PI调节器的转折频率为
(5)
图5给出了PI调节器的波特图。从图5可以看出,在转折频率fL处,PI调节器的幅频特性曲线由90 dB/(°)变为35 dB/(°),相应的相频特性曲线则从-90°单调上升为0°。

图5 PI调节器波特图
由于PI调节器的相位始终为负值,当PI调节器加入系统环路时,会使系统产生一定的负相移,导致系统在截止频率fc处的相位裕度减小。为了减小PI调节器的负相移对相位裕度的影响,一般要求PI调节器的转折fL频率远低于系统截止频率fc。因此,在截止频率fc附近分析PI调节器的幅频特性主要体现为比例特性,即KI/j2πfc≈0。此时Gi(j2πfc)可以用KP替代。
为保证足够的相位裕度,fc要远小于fr,因此在系统的截止频率fc处,滤波电容的容抗远大于网侧电感的感抗,即电容中流过该频率的电流很小,可以认为滤波电容支路是开路的,即1/(sC)=1/(2πfcC)≈∞,滤波器可以简化为单电感的L型滤波器,由此可得系统环路增益A(s)的幅值,可以近似化简为
(6)
又因为,在截止频率fc处,系统环路增益|A(2πfc)|=1,而PI调节器在截止频率fc处Gi(2πfc)≈KP,所以将其带入式(6)可以求得PI调节器的比例环节KP为
(7)
4 系统闭环参数及其约束条件
在进行系统闭环参数设计时,稳态误差、相位裕度、幅值裕度等都是需要考虑的重要性能指标。由图3与式(4)可知,并网电流I2(s)表达式为
(8)
令
(9)
(10)
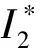
通常,环路增益在基波频率f0处的幅值远大于1。因此,可以认为式(9)中1+A(s)≈A(s),由此可得
(11)
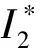
(12)
(13)
对于PI调节器,在基波频率处,起主要作用的是积分环节,因此式(13)中的Gi(2jπf0)≈KI/2jπf0,由此可得
(14)
将式(14)与式(12)带入式(10)中可得
(15)
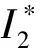
在设计系统参数时,还需要考虑系统的动态响应速率与系统鲁棒性。一般而言,系统相位裕度φm与系统动态响应速率关系密切,而系统幅值裕度kg与系统鲁棒性关系密切。因此,可以根据系统动态响应与鲁棒性要求确定φm与kg值。据此,根据系统对稳态误差、相位裕度、幅值裕度的要求可以分别得到系统对各参数的限制条件,从而选取合适的参数。
另外,当LCL型并网逆变器采用电容电流反馈有源阻尼时,会在系统产生的调制波信号中引入电容电流,而电容电流含有大量谐波,这会导致系统调制波的变化率变大。为避免调制波与载波信号在一个周期内多次交叉,系统通常要求调制波的最大变化率要小于载波的变化率。因此,需要对电容电流反馈系数H1进行限制[10]。
除了根据以上设计指标确定参数外,系统还必须满足劳斯-赫尔维茨稳定判据,根据式(4)可得系统特征方程为
L1L2Cs4+s3L2CH1KPWM+s2(L1+L2)+
H2KPWMKPs+H2KPWMKI=0
(16)
令
(17)
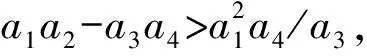
根据以上讨论,在实验室中,逆变器接入电网电压为380 V三相交流电,并设定整流输出的电压Udc为500 V,从而确定系统各参数如表1所示。

表1 三相LCL型并网逆变器电容电流反馈有源阻尼系统参数Table 1 Parameters of capacitor current feedback active damping system for three-phase LCL grid connected inverter
根据式(4)与表1可以得到系统奈奎斯特曲线图,如图6所示。从图6可以看出,所选参数满足系统稳定性要求,并能够较好地满足逆变系统对相位裕度、幅值裕度的要求[11]。

图6 电容电流反馈有源阻尼开环奈奎斯特曲线图
5 LCL型三相并网逆变器的仿真模型
为了验证以上控制策略的正确性,在Matlab/Simulink 中搭建了仿真模型。该电路主要分为两部分,分别为主电路部分与控制器部分。其中主电路中又可分为直流电压、三相逆变桥、LCL滤波器、三相电网等4个部分,而控制器部分也可分为PLL锁相、坐标变换与控制、坐标反变换、PWM信号产生等4个部分。
电容电流反馈有源阻尼控制策略的主电路结构如图7所示,电容电流反馈有源阻尼系统的控制器仿真结构框图如图8所示。
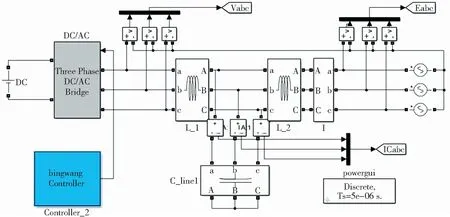
图7 电容电流反馈有源阻尼控制主电路图

图8 电容电流反馈有源阻尼控制器仿真图
图9给出了电容电流反馈有源阻尼的仿真波形。图9(a)与图9(b)分别为半载稳态运行与满载稳态运行的仿真波形;图9(c)为系统在半载与满载跳变时的仿真波形;图9(d)为电容电流反馈有源阻尼控制策略下,旋转坐标系下并网电流波形。根据图9可以看出,在电容电流反馈有源阻尼控制下,并网逆变系统能够稳定运行。

图9 电容电流反馈有源阻尼三相并网电流仿真图
6 结 语
通过建立LCL电容电流反馈并网逆变器数学模型,分析了并网电流稳态误差、相位裕度、幅值裕度等系统性能指标,并最终得到了满足系统动态响应与鲁棒性的系统参数。仿真结果验证了LCL型并网并网逆变器运行可靠性,通过电容电流反馈,减小了并网电流谐波,提高了并网逆变器系统运行稳定性,尤其在系统功率变动的运行工况下,可以有效提高并网逆变器动态调节能力。

