自主光学相对导航中序列图像最优构建方法

孙博文，王大轶，2，周海银，李茂登，王炯琦

(1. 国防科技大学理学院，长沙 410073；2. 北京空间飞行器总体设计部，北京 100094；3. 北京控制工程研究所，北京 100094)

0 引 言

空间目标自主相对导航技术在空间碎片清除[1]、航天器在轨服务[2]、深空探测[3]等领域发挥着重要作用。为了获取更多的测量信息,航天器上往往配备光学相机、激光雷达、微波雷达等多种探测敏感器设备[4]。然而,航天器结构资源有限难以安装过多的探测敏感器,且航天器计算资源受限难以处理过多的测量数据,这两个约束要求航天器必须精简星载探测敏感器。

光学相机具有结构简单、数据丰富等特点,若仅用光学相机作为测量敏感器即可实现自主相对导航,则在降低航天器体积造价、降低计算消耗等方面具有很大的应用空间[5]。所以仅用星载光学敏感器提供的序列图像进行空间目标自主相对导航成为空间导航领域的创新模式,也是当前的研究热点。

然而,仅用序列图像进行自主光学相对导航过程中,由于光学相机无法观测目标的距离信息,导致其组成的自主相对导航系统无法通过测量直接解算得到相对位置参数,所以仅用序列图像的自主光学导航系统为欠观测系统[6]。如何通过序列图像反演出相对距离信息,使此类欠观测系统满足可观测性,能够实现导航参数的完备估计,是自主光学相对导航面临的难点问题[7]。

对于此问题,往往利用可观测性理论判断相对系统状态是否可以被完备估计[8-10]。然而,Woffi-nden等[11]证明了基于Clohessy-Wiltshire (C-W)方程的自主光学相对导航系统不满足可观测性。为使此类系统满足可观测性(即实现状态的完备估计),工程上通常有以下两种方法:一是利用轨道机动方法,二是利用相机安装偏置方法。两种方法均利用虚拟预测方向与实际观测方向的差异构成三角形结构(目标点、虚拟观测点和实际观测点构成的三角形),进而反演相对距离信息,实现相对导航参数的完备估计。

在轨道机动方法中,Woffinden等[12]研究了通过航天器轨道机动分析得到了目标距离信息,Grzymisch等[13-14]讨论了通过轨道机动满足系统可观测性的充要条件,在代数层面上分析了状态预测与机动的代数关系,得到了最优机动。基于轨道机动的自主光学相对导航方法需改变航天器轨道参数,对航天器轨道控制要求高;而且轨道机动需要消耗大量的能源,不利于星上进行连续轨道控制。

在不进行轨道机动的情况下,通过光学相机安装偏置构建序列图像也可实现自主光学相对导航参数的完备估计。相比于轨道机动方法,基于光学相机安装偏置方法无需改变轨道参数,同时减少了轨道机动带来的能源消耗。Geller等[15]分析了基于C-W方程的自主光学相对导航不可观测时的充要条件,利用光学相机安装偏置构建的序列图像实现了系统状态的完备估计,并通过实验定性分析了相机安装偏置中三轴分量对估计精度的影响。在此基础上,Gong等[16]研究了估计精度对相机安装偏置、姿态旋转等因素的敏感性。宋亮等[17]在相机安装偏置条件下对系统进行可观测性分析,提出了一种基于扩展卡尔曼滤波的自主相对导航方法。

然而,在利用光学相机安装偏置构建光学序列图像进行系统状态完备估计时,上述文献均没有考虑序列图像构建对自主光学相对导航精度的影响。在测量噪声和状态预测协方差共同影响下,目标点、虚拟观测点和实际观测点所构成的三角形几何属性对相对导航状态估计精度有着极其重要的影响。例如,极限条件下,若虚拟预测方向与实际测量方法重合,则无法构成三角形结构,此时系统仍不满足可观测性。所以,为了进一步提高自主光学相对导航精度,需要以系统可观测度为指标,探索利用光学相机安装偏置来实现光学序列图像的最优构建方法。

针对此问题,本文在利用光学相机安装偏置实现自主相对导航的条件下,提出了一种基于几何属性量化的自主光学相对导航序列图像最优构建方法。首先通过分析自主光学相对导航系统可观测性,探究了影响估计精度的关键因素,然后依据状态估计误差的几何特性建立了相对导航系统可观测度指标,并在此基础上量化了该指标与序列图像构建方式的映射关系,研究了序列图像最优构建方法,给出了相应的导航滤波算法,提高了自主光学相对导航精度。

1 自主光学相对导航系统模型

1.1 坐标系定义与转换

本节定义相关坐标系,如图1所示。

图1 坐标系

轨道系FO：原点为航天器质心,xO轴由地心指向航天器质心,zO轴垂直于轨道平面并平行于航天器的角动量矢量,yO轴与xO,zO轴构成右手系。

本体系FB：原点为航天器质心,三轴固定且已知,构成右手系。

相机系FC：原点为相机镜头中心,zC轴为光轴方向并指向外,xC轴与yC轴均与相机成像平面的平行,构成右手系。

文中利用上标O,B,C分别表示向量在FO, FB, FC下的表示。坐标系转换定义如下:

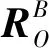
2) FB到FC的转换:如图1所示,FB和FC之间不仅存在旋转还存在平移,空间目标在两坐标系下的位置矢量分别表示为rB和FC,两者之间存在如下转换关系

(1)

1.2 相对运动状态方程

航天器与空间目标在轨运行时,可以在轨道系下建立两者的相对运动状态方程。令rO=[x,y,z]T为轨道系下目标的相对位置矢量,当航天器与目标距离远小于地心距且航天器与空间目标轨道均为近圆轨道时,相对运动状态可用C-W方程表示[18]

(2)

(3)

式中:

(4)

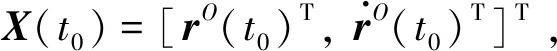
X(t)=Φ(t,t0)X(t0)

(5)

式中:

τ=n(t-t0),s=sin(τ),c=cos(τ)

(6)

1.3 光学测量方程

(7)

由于光学相机测量仅为目标的方向矢量,无距离信息,则测量方程为

(8)

式中:ν∈3为测量噪声;表示向量的2-范数,值为向量的欧氏模长。

根据式(7)和式(8),可知观测矩阵为

(9)

由式(8)可知,光学相机仅测量空间目标相对于相机的方向矢量,无距离信息,无法通过单次测量解算出相对位置矢量。为了实现相对导航状态的完备估计,下面首先进行自主光学相对导航系统可观测性分析,并在此基础上研究序列图像的最优构建方法。

2 序列图像最优构建

2.1 自主光学相对导航系统可观测性分析

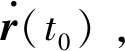
(10)

此时光学相机测量方程为

(11)

由于光学相机无法测量距离信息,若将t0时刻的相对运动状态扩大ρ倍,则t时刻的测量为

(12)

z(t)=zρ(t)

(13)

为了使系统满足可观测性,并可以实现高精度自主相对导航。从提升系统可观测能力方面讨论如何在现有条件下实现最优估计。首先构建相对导航系统可观测度指标,后在其指导下星上自主构建序列图像。

2.2 自主光学相对导航系统几何特性分析

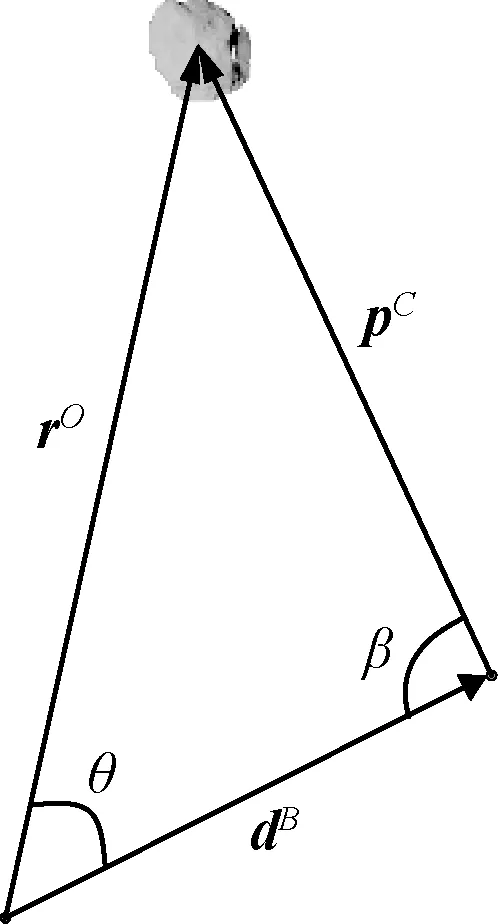
图2 相对导航三角构型

根据三角形正弦定理可得

(14)

式中:

(15)

根据式(14),可知两角度θ和β的关系,令

(16)

式中:

(17)

2.3 序列图像星上自主构建

由文献[15]可知,图2所示的相对导航三角构型影响相对导航的估计精度,下面通过设定可观测度指标,研究如何调整相对导航三角构型可以得到高精度的相对导航估计结果,即序列图像如何星上自主构建。

在Kalman滤波框架下实现相对导航状态的估计,需要利用光学相机的测量值对状态预测值进行更新。其中状态预测值可由C-W状态方程递推得到,本文主要考虑光学相机测量中序列图像构建方式对估计精度的影响。

滤波过程中状态预测值存在预测误差,光学相机对空间目标进行观测时存在测量误差。假设两误差均服从正态分布,标准差分别表示为Δθ和Δβ。标准差范围内,目标相对位置的估计误差如图3所示的阴影部分。

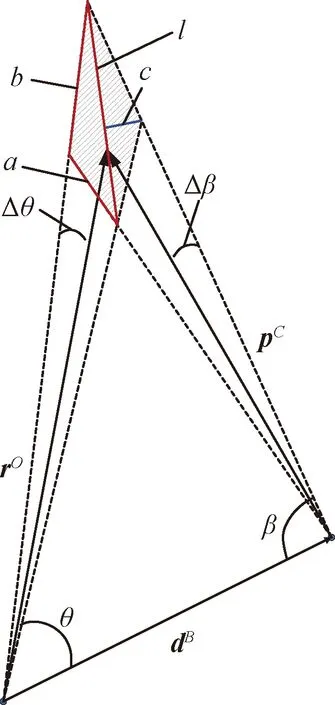
图3 相对位置估计误差

由于目标与航天器的距离远远大于相机安装偏置长度,则图3中阴影部分形状细长。令阴影部分内的点与长对角线l的最远距离为c,满足

(18)

易知,

a+b≥c

(19)

同理,由于目标与航天器的距离远远大于相机安装偏置长度,则可近似认为θ+β≈π,此时对角线长度l可近似为

l≈a+b

(20)

进一步地,

(21)

此时以阴影四边形的长对角线长度l的倒数为可观测度,即认为当长对角线的长度最小时可观测度最大。由于角度θ和β存在函数关系,如式(16)所示。则l可以看做角度θ的函数,为了使得对角线长度l最小,需求

θ=argminl(θ)

(22)

长对角线l的长度最小时有

(23)

注1. 相对导航状态滤波过程中,可以得到轨道系下相对位置预测值的协方差Prr,可参照文献[19]将位置矢量的误差转化为方向矢量的误差,即可计算图3所示的平面中的角度标准差Δθ。

2.4 相对导航状态估计算法

针对式(5)与式(8)组成的自主光学相对导航系统,假设tk时刻的过程噪声方差为Qk,测量噪声方差为Rk,状态协方差矩阵为Pk。上标+和-分别表示变量的估计值和预测值。将tk-1时刻到tk时刻的状态转移矩阵用Φk/k-1表示。下面给出状态滤波算法步骤。

初始化:当k=0时,令

(24)

状态预测:

(25)

状态更新:

(26)

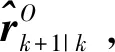
计算旋转轴

(27)

(28)

计算旋转角度

(29)

故旋转矩阵对应的四元数为

(30)

(31)

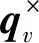
3 仿真校验

文中设置仿真实验验证本文提出的基于可观测度量化的自主光学相对导航序列图像最优构建方法。实验场景选自原型研究仪器与航天技术进步任务(PRISMTA)。以Mango为服务航天器,Tango为非合作目标,自主光学相对导航任务开始时间为2012年5月12日4∶00UTC。轨道根数如表1所示,轨道系下相对轨道与目标距离如图4所示。

表1 轨道根数

图4 相对位置轨迹

设置相机安装偏置位于航天器本体系dB=[1, 1, 1]T处,假设安装旋转矩阵可以转动且已知。根据图4可知,航天器与目标距离远远大于相机安装偏置长度,依据文中提出的可观测度指标,仿真得到此相对导航场景下最优的角度θ和角度β。

如图5所示,角度θ和角度β满足式(23)中得到的结论。进一步,与20组随机设置的夹角θ进行对比实验(服从均匀分布),相对位置估计误差如图6所示,相对速度估计误差如图7所示。

图5 最优角度

图6 位置估计误差

图7 速度估计误差

图6和图7中,红色带点实线表示本文提出以对角线长度为指标的估计误差结果。可以看出本文提出序列图像构建方法优于随机生成的序列图像。进一步,分别统计本文提出方法与随机生成中最优的估计平均绝对误差(MAE)。

从图6、图7以及表2、表3中可以看出,当航天器与目标距离远远大于相机安装偏置长度时,相比于随机生成的序列图像,提出的序列图像构建方法可以使相对导航状态估计更好地收敛,而随机生成的序列图像中甚至存在滤波发散现象。通过仿真实验验证了本文提出方法的有效性。

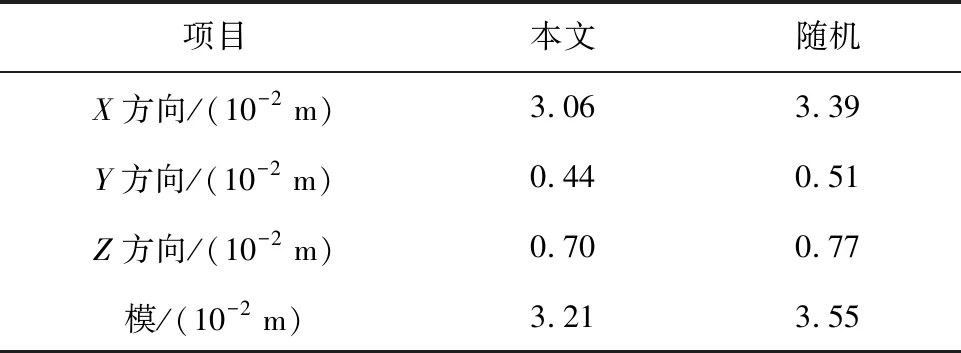
表2 相对位置平均绝对误差

表3 相对速度平均绝对误差

4 结 论

本文提出了一种基于可观测度量化的自主光学相对导航序列图像最优构建方法,通过量化误差几何属性并以此作为可观测度指标指导了序列图像构建方式,最终实现了高精度的自主光学相对导航。通过理论推导和仿真实验,可以得到以下结论:

1) 系统可观测度与角度θ相关,可以通过量化系统可观测度(状态估计误差几何特性)给出最优角度θ的值;

2) 相对于随机构建的序列图像方法,本文提出的序列图像最优构建方法可有效提高自主光学相对导航精度;

3) 本文虽以基于相机安装偏置的自主光学相对导航为背景,但提出的方法也可应用于通过轨道机动实现自主光学相对导航的方法中。