组合式气囊在重装空投中的缓冲性能分析
鲁超宇,陈金宝,2,3,王 宸,2,3,朱锦耀,黄梓瀚
(1. 南京航空航天大学航天学院,南京 211106;2. 深空星表探测机构技术工信部重点实验室,南京 211106;3. 航天进入减速与着陆技术航天科技集团重点实验室,南京 211106)
0 引 言
重型装备空投技术可大大提高空降部队的作战能力,其中着陆缓冲系统是保障重型装备在空投环境中安全着陆最重要的技术之一。目前国际广泛应用气囊缓冲系统应对伞降减速后装备的残余速度[1],一般为独立气囊或主/辅单气囊结构,其具有结构简单、可靠性高等优点。由于空投试验成本高昂、可重复性差,目前针对缓冲气囊的研究多数集中在解析分析和仿真分析两个方面,学者们也对此进行了大量研究[2-6]。刘鑫等[7]提出基于概率-椭球混合模型的缓冲气囊防护可靠性分析方法;洪煌杰等[8]通过仿真和代理模型方法对气囊系统进行多目标优化;Cao等[9]基于离散元方法对球形气囊进行了跌落缓冲仿真分析;He等[10]基于相似关系推导了球形气囊缓冲冲击响应并与地面原型进行了相似性分析;张鹏飞等[11]基于有限元方法讨论了单参数变化对气囊缓冲效果的影响。
虽然单气囊缓冲方式能够满足现阶段普通工况空投装备过载要求[12],但面对高海拔地区和复杂地形环境时,装备过载会大幅升高,极易超过装备允许过载[13]。且随着未来战场环境的不确定性增加、我国空降部队规模和军事实力的增强,即将服役空投的二代战车装备质量将大幅提升,同时车内将携带更多精密设备,甚至未来面向载人空投技术的研究[14],均要求缓冲过程中装备过载进一步降低。现阶段的缓冲气囊在排气完毕时,装备依然存在一定的垂直速度,并与地面发生硬碰撞[15]。所以进一步研究降低空投装备着陆过载水平、避免装备与地面发生硬碰撞的缓冲气囊结构具有较大意义。
由于仪器精密和载人需求,组合式气囊在航天器和返回舱着陆缓冲领域已有应用[16],如ILC Dover公司和ASNS公司设计的组合式气囊着陆缓冲系统,在航天着陆领域均表现出优异的缓冲性能[17-18];Zhou等[19]设计了新型月球着陆组合式缓冲气囊,并分析了其缓冲性能与参数响应。对组合式气囊的研究证实了其具有良好的排气后支撑性,有利于在外气囊排气后进一步降低载荷过载。但现有组合式气囊缓冲的资料中,迄今为止尚无将组合式气囊应用于重装空投缓冲以避免装备与地面硬碰撞的方法研究,缺乏组合式气囊缓冲效果的清晰结论,且针对组合式气囊的精密解析分析和仿真方法也未见详细分析。
针对以上问题,为详细论证组合式气囊在重装空投领域的应用价值,本文通过理论分析和有限元仿真的方法,详细剖析现阶段空投装备单气囊缓冲的局限性和组合式气囊在空投装备缓冲领域的应用构型及其缓冲机理、多工况缓冲效果,并探究内气囊结构参数对缓冲效果的影响趋势。结果表明,组合式气囊在空投装备高速触地缓冲中可进一步有效降低空投装备过载,在多工况场景中有更加出色的应用。
1 现役空投装备缓冲方案分析
1.1 气囊缓冲模型
现役某型空投装备战斗全重约为8 t,其应用的单体缓冲气囊和所提出的组合式气囊结构如图1所示,为主/辅气囊结构,主辅气囊之间有通气孔,辅气囊有排气孔连通外界,主气囊下方进气口用于空降过程气囊自充气,组合式气囊内部增加一密闭圆柱形气囊。

图1 单气囊与组合式气囊结构
单气囊与组合式气囊在外气囊压缩排气过程中情况一致,气囊着陆压缩过程中,排气孔的开启阈值为标准环境压力。辅气囊不直接参与载荷承接,而是起到延缓主气囊气体排出、增加着陆稳定性的作用。由于存在排气情况,气囊织物弹性影响较小,不予考虑。
主气囊通气孔和辅气囊排气孔均可看作薄壁孔排气模型[20],对于主气囊
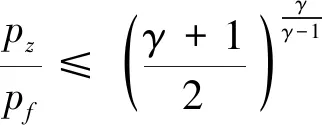
(1)

(2)

同理,对于辅气囊

(3)
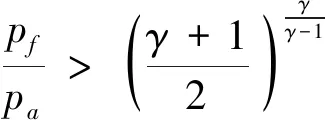
(4)
主气囊压缩过程中有如下参数关系
Vz=Ahz
(5)
(6)
(7)
式中:A为主气囊顶部和底部面积平均值,即缓冲过程中装备与气囊平均接触面积;Vz为主气囊体积;Vz0为主气囊初始体积;mz为主气囊气体质量;mz0为主气囊初始气体质量;pa为环境压力;pf0为辅气囊气压;Akf为辅气囊排气孔面积;Tf0为辅气囊气体初始热力学温度;hz为主气囊高度。
辅气囊缓冲过程中不直接受载荷压缩,吸收主气囊排出气体后进一步排出,有如下参数关系
(8)
(9)
(10)
式中:Vf为辅气囊体积;Vf0为辅气囊初始体积;mf为辅气囊气体质量;mf0为辅气囊初始气体质量;hf0,hf分别为辅气囊初始高度、辅气囊高度。
空投装备着陆缓冲过程中运动方程为
Ma=(pz-pa)A-Mg
(11)
式中:M为空投装备质量;a为装备竖直方向加速度;g为重力加速度。
1.2 算例分析
基于控制体积法建立单一气囊、1/10质量载荷算例,以验证仿真算法的正确性,算例参数如表1所示。
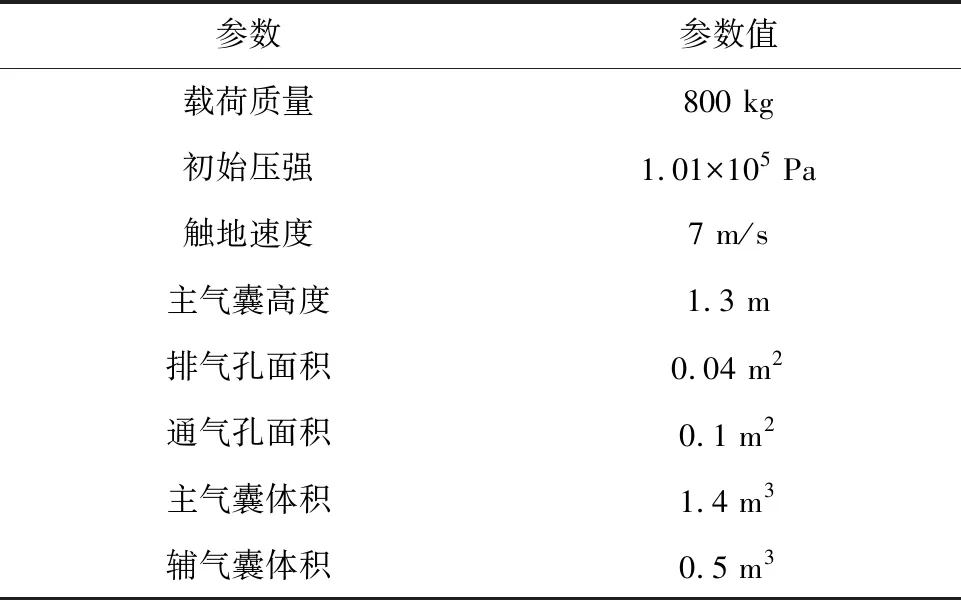
表1 算例参数
定义竖直向上方向为正,获得载荷主/辅单气囊着陆缓冲过载曲线如图2所示,基于控制体积法建立有限元模型与解析模型进行对比,从图中可以看出,载荷过载响应仿真与模型基本一致,少量误差是由于解析模型忽略了气囊织物弹性和相关接触特性。本仿真方法可适用于空投装备仿真分析,具有较高的可靠性。
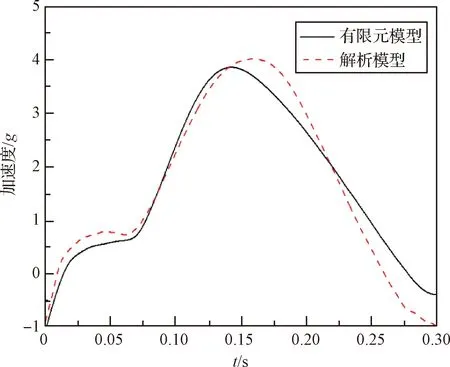
图2 算例过载加速度曲线
1.3 单气囊缓冲过程有限元仿真分析
基于上述有限元建模方法,并参考现有空投缓冲气囊参数[21]建立重装空投单气囊缓冲有限元模型,相关参数如表2所示。
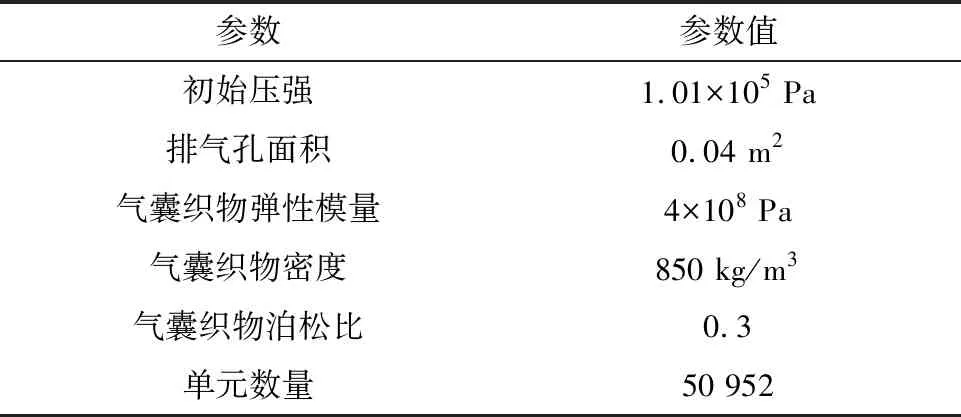
表2 有限元模型参数
分别计算触地速度为5、7、9 m/s时的装备过载,过载曲线如图3所示,可以看出,随着触地速度的提高,装备过载急剧攀升,呈现出明显的双波峰现象,且越来越尖锐,趋势与文献[21]一致。
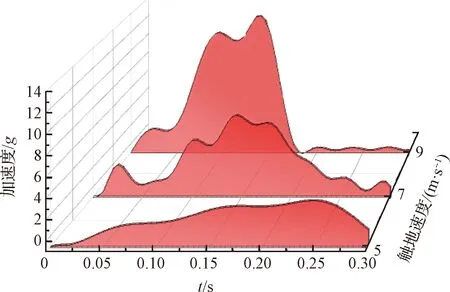
图3 不同触地速度下装备过载加速度
以9 m/s触地速度为例进行分析,0 s空投装备气囊系统开始触地,气囊急剧压缩同时伴随排气孔排气,在0.09 s时出现第一个过载加速度波峰约11.94g,此时气囊对载荷的缓冲作用力达到最大;随后在0.14 s时,随着囊内气体排空,装备隔着气囊织物与地面发生硬碰撞,此时过载达到最大值13.72,装备残余竖直速度迅速归零;在0.2 s时整个缓冲过程已完全结束,装备离地发生少量反弹,之后过载逐渐稳定并趋于重力加速度。
通过以上分析不难发现,气囊气体排空后装备与地面的硬碰撞是导致过载急剧升高的主要因素,相关文献也指出,现阶段空投装备的缓冲方法一般都会和地面发生硬碰撞,但由于最大过载处于允许区间内[22],进一步降低过载的研究则相对缺乏。
2 空投装备组合式气囊缓冲性能分析
在遇到极端空投情况如高海拔、复杂地形情况时,传统气囊缓冲效果往往不佳,而缓冲失败代价高昂,损伤严重。且随着空投装备质量在未来进一步提升、更多精密设备的携带,考虑未来载人空投的发展趋势,降低空投装备过载的方式需要进一步研究。而单纯提高气囊高度会导致着陆不稳定甚至侧翻,在保证气囊整体尺寸不变的情况下,组合式气囊则可以最大限度避免硬碰撞导致的过载激增[23],对空投装备提供有效支撑。
2.1 内气囊绝热压缩过程分析
组合式气囊整个缓冲过程涉及内、外气囊两部分的先后缓冲。可分为两个阶段进行分析:外气囊排气释能阶段、内气囊绝热压缩阶段。第一阶段与上述模型相同,第二阶段从内气囊压缩参与缓冲开始,到装备开始反弹结束。
以单个圆柱形密闭内气囊为分析对象,由于内气囊密闭不排气,不再从气体流量角度进行分析,转而分析载荷受力模型和气囊织物力学性能,相对于排气型外气囊,内气囊织物拉伸、剪切应力作用较明显,分析中考虑织物环向应力和轴向应力作用。气囊作为缓冲系统可有效隔绝冲击中的高频成分,可将空投装备载荷简化为刚体模型[24],假设内气囊压缩过程中的变形理想对称,压缩模型如图5所示。
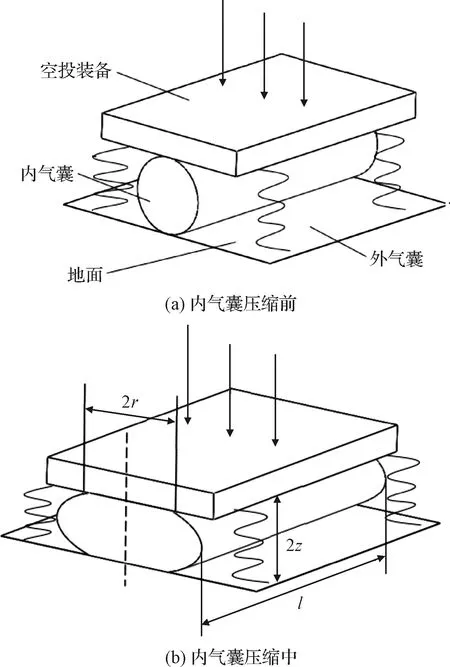
图5 内气囊绝热压缩示意图
压缩过程中,气囊织物截面弹性拉伸后长度约为
L=2πz+4r
(12)
式中:z为内气囊高度的1/2;r为内气囊与载荷接触部分截面长度的1/2;z0,r0为z,r初始尺寸;l为内气囊轴向长度。
整个缓冲压缩过程中,织物径向和环向始终处于张紧状态,根据假设中内气囊对称压缩,内气囊织物始终受到环向应力σh和轴向应力σt,沿气囊壁轴向平衡方程有
(13)
式中:pn为内气囊内压;pz为内气囊外部压力(外气囊内压);hn0为气囊织物厚度。
假设气囊为各向同性线弹性织物,在两种应力作用下,应变分别为
(14)
式中:E为织物弹性模量;μ为织物泊松比。
结合式(13)、(14)可得
(15)
第二阶段内气囊缓冲过程中,装备平衡方程为
(16)
式中:x为第二阶段装备竖直位移;An为装备与内气囊接触面积。
将式(16)在某一位移点进行泰勒展开并忽略二阶及以上小量可得考虑织物弹性的装备平衡方程为
(pn-pz)An-Mg
(17)
压缩过程中内气囊体积约为
Vn=l(4rz+πz2)
(18)
对体积求微分得
(19)
(20)
内气囊压缩过程可逆绝热,则有
(21)
联立式(15)、(20)、(21)并忽略二阶以上小量,在缓冲过程中气囊参数有如下变量关系
e1+e2Δr+e3Δz=0
(22)
式中:Δr, Δz为缓冲过程中相关参数某一阶段变化量;e1,e2,e3为代数量,可由已知参数表示。
由于假设气囊对称压缩,压缩过程中有
(23)
将式(23)代入式(22)可得
(24)
在压缩过程中任意时刻内, 气囊几何参数之间存在如下关系
(25)
且由于pnVn=pn0Vn0,可得
(26)
联立式(20)、(25)、(26)和式(17)的广义力形式可得
(27)
基于上述理论分析可知,第二阶段密闭气囊缓冲实质为一单自由度广义非线性受迫振动,可有效隔绝第一阶段残余速度下的装备着陆冲击,进一步对装备残余速度进行缓冲。
2.2 组合式气囊缓冲过程有限元仿真分析
建立组合式气囊有限元模型,其中内气囊直径0.3 m,密闭不排气,隐去一侧外气囊如图6所示,其余仿真参数与单气囊模型相同。
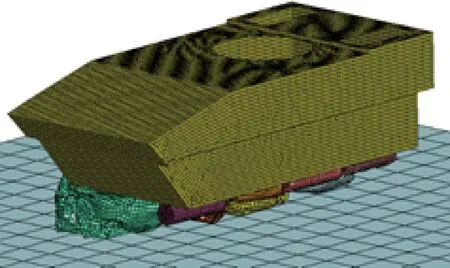
图6 组合式气囊缓冲有限元模型
设定竖直触地速度9 m/s,水平速度0 m/s,地面坡度0°。通过显式动力学分析获得组合式气囊缓冲装备过载和速度变化,与单气囊缓冲对比如图7、图8所示。

图7 组合式气囊与单气囊装备过载加速度对比
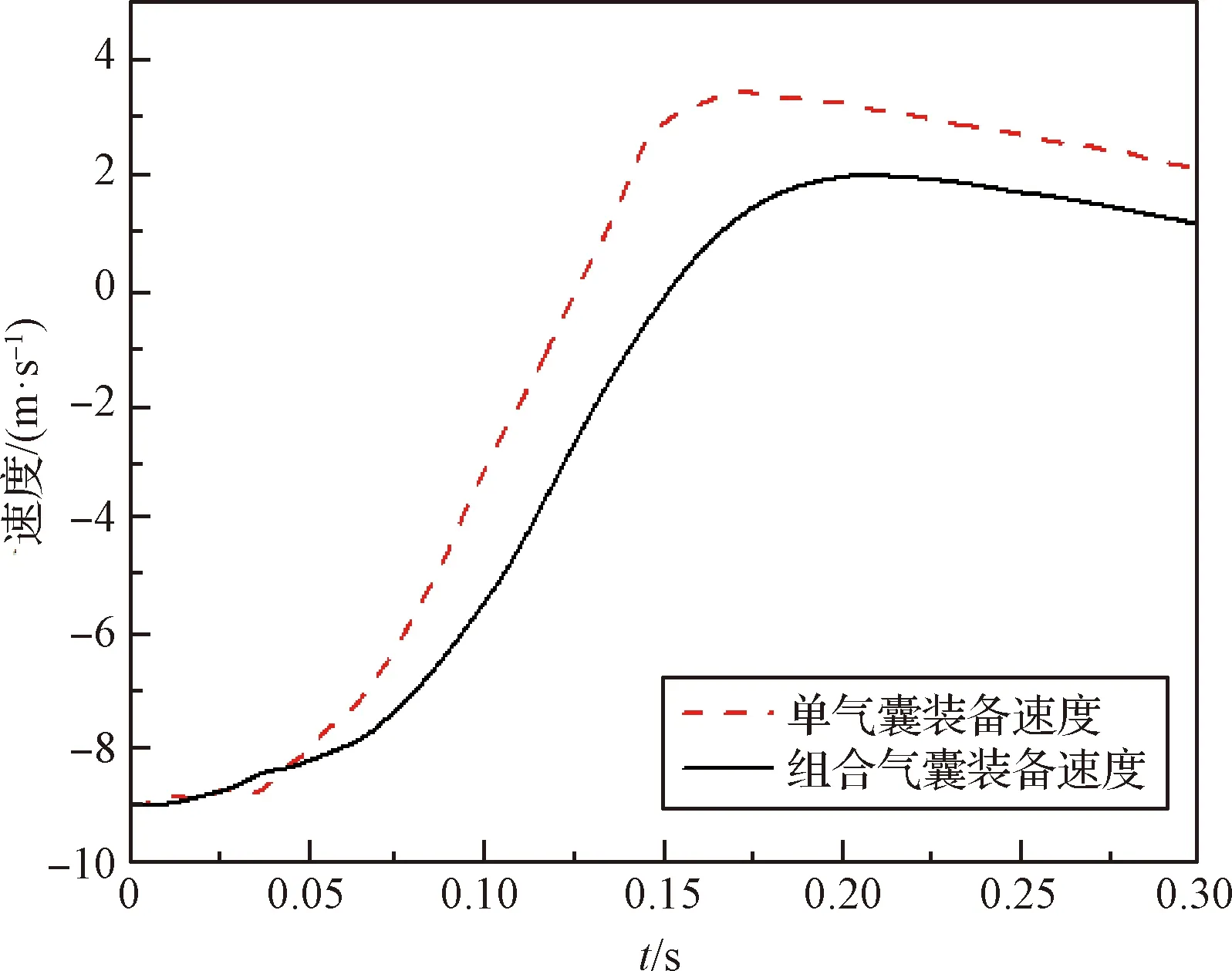
图8 组合式气囊与单气囊装备速度对比
组合式气囊下装备过载在0.13 s时达到最高,为11.96,随后开始下降,在0.22 s时装备达到最大反弹速度。可以看出,同等着陆条件下,组合式气囊装备过载双峰现象几乎消失,过载提升相对稳定,相对于单气囊缓冲造成载荷与地面硬碰撞导致的最高过载降低约12.83%,最高反弹速度降低约40.1%。可有效提高空投装备着陆的安全性和稳定性。
受着陆地形坡度和空投风速影响,难免出现非正常着陆工况,为验证组合式气囊的适用性,以图9有限元模型为基础,进一步进行竖直触地速度9 m/s,水平横向速度5 m/s,地面坡度0°和竖直触地速度9 m/s,水平横向速度0 m/s,地面坡度5°两种特殊工况下的单气囊缓冲和组合式气囊缓冲仿真分析,如图9~图12所示。

图9 水平速度特殊工况装备过载加速度

图10 水平速度特殊工况装备竖直速度
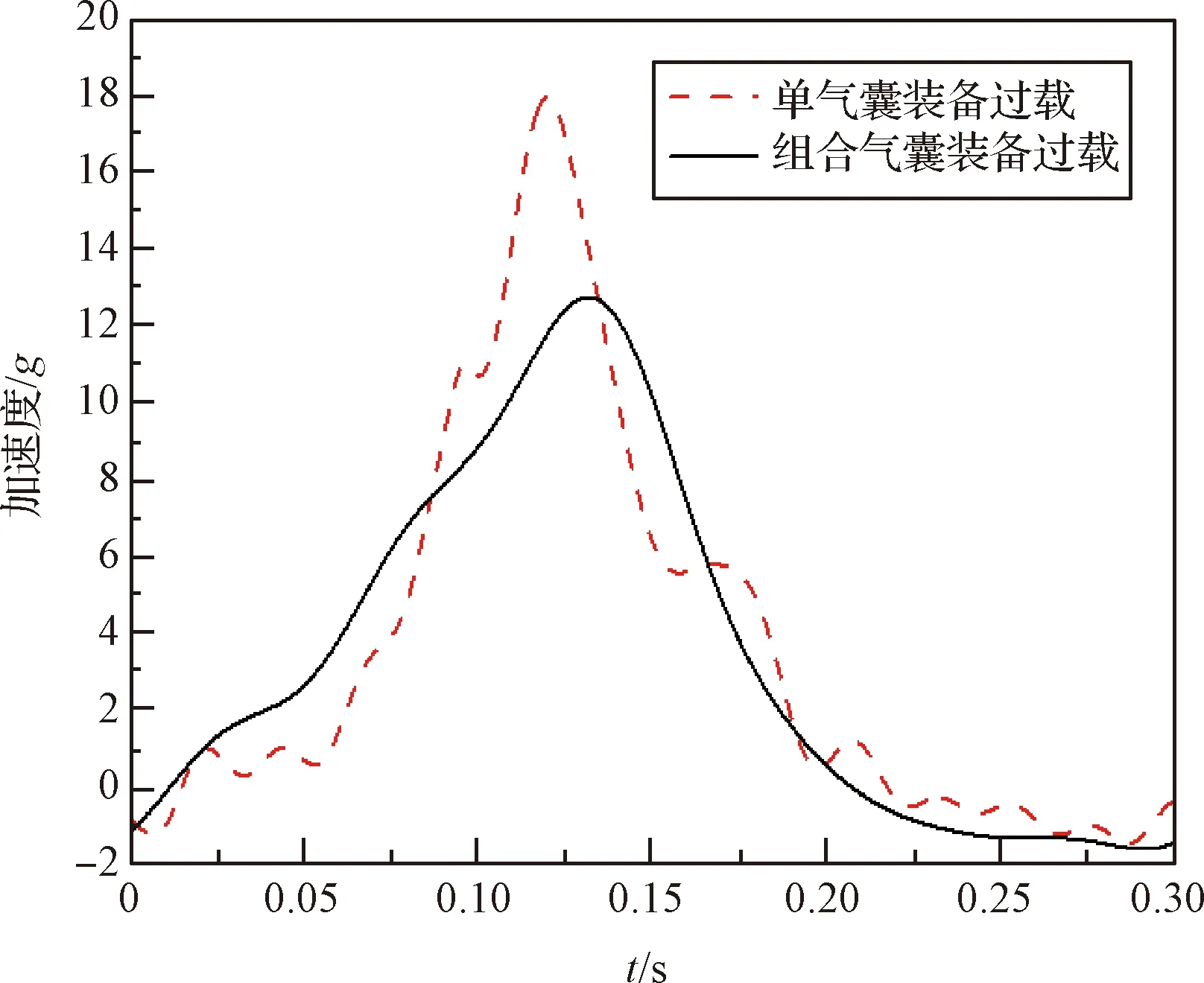
图11 地面坡度特殊工况装备过载加速度

图12 地面坡度特殊工况装备竖直速度
当载荷同时存在水平速度触地时,整体高过载时间更加短促,也导致反弹速度相比仅有竖直速度时较低,但水平速度使得速度方向另一侧气囊压缩略微不充分,单气囊和组合式气囊缓冲载荷整体过载均略微提高,但组合式气囊优势依然明显。单气囊缓冲最高过载为14.82,组合式气囊缓冲最高过载为13.38,降低约9.7%。
当着陆地面存在明显坡度时,对空投行动来说是较为危险的情况,通过上图可以发现,单气囊缓冲情况下载荷过载明显提高,达到18.32。而组合式气囊性能出色,载荷过载约12.84,降低29%,但高过载持续时间较久,过载变化平稳,这也导致两者反弹速度差别不大。由于着陆地面存在坡度,一侧气囊首先触地,承受巨大冲击导致该侧气囊排气首先结束,同时提供翻转力矩,而此时另一侧气囊缓冲尚不充分,在0.12 s时载荷一侧与地面首先发生碰撞带来较高过载,随后的0.17 s时另一侧气囊排气完毕,装备与地面二次碰撞,产生过载小波峰。而组合式气囊由于内气囊的存在,有效避免了这类情况对载荷的影响,缓冲整体平稳,过载较低,具有出色的表现。
3 组合式气囊参数对缓冲效果的影响
缓冲气囊结构中加入密闭内气囊,可能会导致气囊主要参数变化对整体缓冲效果的影响趋势发生改变。现役单气囊缓冲系统结构参数已广泛应用,在不改变缓冲系统整体结构尺寸的基础上分析内气囊直径和外气囊排气孔面积变化下的装备过载变化趋势。现役空投装备战斗全重为8 t,9 m/s为其正常工况下极限触地速度[25],以此速度普通工况和现有模型参数作为初始条件,在一定范围内,采用全因子法以固定间隔进行36组仿真分析并拟合结果,分析装备过载变化趋势和分布规律,组合参数如表3所示,获得结果如图13。

表3 仿真设计方案及结果

图13 装备最高过载加速度随气囊参数变化趋势
对曲面图分析可知,装备最高过载随内气囊直径和外气囊排气孔面积两个参数的增大整体呈现先降低后升高的趋势。随着内气囊直径的增大,降低了装备与地面硬碰撞导致的过载激增,但外气囊体积被过多侵占,内气囊介入过早,导致排气量不足,影响初始阶段缓冲效果,导致整体缓冲效果越来越差;而随着外气囊排气孔面积的变化,最佳的内气囊直径也略有不同,综合看来,当内气囊直径为0.25 m,外气囊排气孔面积为0.04 m2时,缓冲效果最佳,装备最大过载为11.13,进一步降低6.93%,与单气囊缓冲方式相比,最高过载降低18.87%。
由以上分析可知,内气囊虽然可以避免硬碰撞情况,但其尺寸不宜过大;组合式气囊中排气孔面积引起装备过载的变化趋势与单气囊过载变化趋势相似。所以实际工程应用中,应根据载荷情况选取合理的相关参数以取得最佳缓冲效果。
4 结 论
基于空投装备缓冲更低过载需求的必然趋势,提出重装空投组合式气囊缓冲方法,详细剖析了缓冲机理并进行多工况仿真分析,主要结论如下:
(1) 现役空投装备气囊缓冲在较高触地速度9 m/s时,最高过载达到13.72,证实了存在装备与地面发生硬碰撞的局限性;
(2) 多工况下组合式气囊均能有效降低装备着陆冲击,在内气囊直径0.3 m、外气囊排气孔面积0.04 m2典型工况下,相对传统单气囊缓冲最高过载降低约12.83%,最高反弹速度降低约40.1%,可有效提高空投装备着陆的安全性和稳定性;
(3) 装备最高过载随内气囊直径和外气囊排气孔面积的增大总体呈现先降低后升高的趋势。当内气囊直径为0.25 m、外气囊排气孔面积为0.04 m2时,缓冲效果最佳,装备最大过载为11.13,进一步降低6.93%,与单气囊缓冲方式相比,最高过载降低18.87%。极大改善空投装备过载情况,为下一代空投战车和未来载人空投缓冲方案提供了有力的前置缓冲优化措施。

