再入滑翔飞行器俯冲段智能博弈机动策略

蒋庆吉，王小刚，白瑜亮，李 瑜

(1. 哈尔滨工业大学航天学院，哈尔滨 150001；2. 北京空天技术研究所，北京 100074)

0 引 言

再入滑翔飞行器(Reentry glide vehicle,RGV)凭借其特殊的飞行速域和空域正成为当前航空航天领域的研究热点[1-4]。与此同时,以爱国者-3为代表的各类典型防空反导拦截系统正在升级换代以应对高超声速武器的威胁,应对再入滑翔飞行器的拦截方法也在不断更新[5-8]。高超声速武器打击的战略价值目标周围通常布有严密的防空拦截系统,如何在规避拦截器的前提下仍能精确命中既定目标成为当前亟待解决的问题。

再入滑翔飞行器的机动策略一般包括程序式机动[9-10]、基于最优控制理论等的解析机动[11-12]与弹道优化[13]等方法。近年来,许多学者针对再入滑翔飞行器俯冲段的机动策略进行了广泛研究。Shen等[3]将考虑终端目标的轨迹优化问题依次转化为非凸最优控制问题和二阶锥规划问题,提出一种可变信赖域的连续二阶锥优化方法,在时间消耗和最优性之间取得平衡。王洋等[11]通过制导误差与法向机动速度构造滑模面,提出了一种新型机动制导律,在保证导弹末段打击精度的同时提高了机动能力。Sun等[12]基于微分博弈理论研究了包含攻击者、目标和防御者的最优制导律。朱建文等[14]在俯冲平面及转弯平面内分别设计了正弦形式的视线角参考运动,以落速最大为性能指标,利用最优控制对其进行跟踪,机动突防最优制导方法,能够实现机动飞行,且能够高精度地满足终端落角及落点约束。李静琳等[15]针对再入滑翔飞行器再入末段机动与精确打击问题,从最优控制角度出发,提出了一种考虑拦截弹动力学特性的最优机动突防弹道优化方法,获得了再入滑翔飞行器的最大机动能力。再入滑翔飞行器在俯冲段面临各种拦截器威胁从而无法精确命中目标,因此有必要开展俯冲段博弈机动研究以规避拦截并完成打击任务。

现有文献通常假定拦截器模型已知,在特定场景条件下进行突防制导律推导,所得结果往往具有一定局限性。在实际博弈机动中面临的问题有:1)拦截器发射窗口未知,再入滑翔飞行器完成对拦截器的机动之后不一定具备修正落点偏差至零的能力;2)由于探测设备约束,再入滑翔飞行器较难连续不间断获取拦截器信息,信息更新具有一定周期性;3)拦截器未建模动态和实际飞行差异带来的不确定性问题:在解析方法中通常假设拦截器以固定导引系数对再入滑翔飞行器进行拦截,然而在真实战场环境下,往往难以获取对方制导律参数,这将使解析方法存在建模偏差,造成实际飞行的反拦截任务失败;4)计算效率问题,作战环境瞬息万变,需要再入滑翔飞行器在较短时间内即给出机动参数,传统优化方法难以完成在线实时输出最优解。

深度强化学习算法是近年来发展迅速的一类人工智能算法,其在处理序贯决策问题方面具备天然优势。深度强化学习算法在机械臂控制[16-17]、导弹拦截制导设计[18-19]、无人机航迹规划[20-21]、航天器姿态控制[22]等领域得到广泛应用,对解决传统优化算法计算耗时长、局部收敛等问题上取得较好效果。深度强化学习算法将决策问题描述为马尔科夫决策过程,智能体根据观测到的环境状态输出决策动作,动作作用于环境模型产生奖励和状态更新[23]。其中,应用于连续状态空间、离散动作空间的经典算法是深度Q学习(Deep Q-learning,DQN)算法[24],应用于连续状态空间、连续动作空间的是深度确定性策略梯度(Deep deterministic policy gradient,DDPG)算法[25-26]。为解决稀疏奖励问题,Schaul等[27]基于DQN算法提出优先经验回放(Prioritized experie-nce replay,PER)方法。PER大大改善了样本利用效率,在自动驾驶[28]、船舶避障[29]、无人机空投决策[30]等问题上取得较好效果。

为借助深度神经网络解决复杂状态空间序贯决策问题,将再入滑翔飞行器在俯冲段的机动飞行过程建模为马尔科夫过程,对状态、动作、奖励等基本要素进行适应性设计。针对连续状态空间和动作空间的特点,选取DDPG算法对飞行器的智能机动参数进行训练。由于再入滑翔飞行器在被拦截或命中目标点之前缺乏奖励信号,深度强化学习算法的训练面临稀疏奖励问题。在传统DDPG算法的基础上进行多项改进,结合优先经验回放方法对时序差分绝对值较高的样本经验进行优先回放,对高价值样本进行多次利用,从而提高样本利用效率,实现决策网络的快速收敛。仿真表明,收敛后的机动决策网络能够输出稳定有效的机动参数,在典型场景完成对拦截器规避后精确到达目标点,并且调用决策网络时间较短,能满足弹载计算机实时要求。

1 再入滑翔飞行器俯冲段博弈机动仿真数学模型

1.1 再入滑翔飞行器数学模型

不考虑地球自转,再入滑翔飞行器在俯冲段的动力学方程如下:

(1)

式中:V为速度;D为阻力;m为质量;g为引力加速度;γ为路径角;L为升力;σ为倾侧角;r为地心距离;ψ为航向角;θ为经度;φ为地心纬度。在速度、高度确定的情况下,D,L的大小取决于当前时刻攻角α。

飞行器的剩余航程RL计算为

RL=Rearccos(sinφsinφtar+cosθcosθtarcos(θ-θtar))

(2)

式中:θtar和φtar为目标经度和纬度;Re为地球半径。

1.2 拦截器数学模型

在发射坐标系(惯性系)和弹道坐标系下,拦截飞行器运动学与动力学方程如下:

(3)

式中:XI,YI,ZI为拦截器的位置在发射系下的直角坐标分量;VI为速度大小;θI为弹道倾角;ψI为弹道偏角;ny,nz为弹道系下的过载分量。

拦截器采用比例导引律对再入滑翔飞行器进行拦截,制导律的形式为

(4)

在碰撞时刻,拦截器的零控脱靶量计算如下:

(5)

式中:Rrel,Vrel为相对位置和相对速度矢量。

约束模型:考虑拦截器的单通道最大过载约束为NImax,实际过载应满足

(6)

式中:ny为弹道系下法向过载,nz为弹道系下横向过载,满足aI=[ny,nz]T;NImax取为20。

1.3 博弈机动场景随机模型

首先对再入滑翔飞行器与拦截器的博弈机动飞行场景作如下假设:

1)再入滑翔飞行器航向角偏差为0,在不机动飞行且无拦截器时可在射面内导引命中目标点;

2)拦截器发射位置分布在再入滑翔飞行器目标点周边,且第一次被再入滑翔飞行器探测到时已完成主动段飞行,位于一定高度位置;

3)再入滑翔飞行器在碰撞前10 s开始进行机动飞行,且获取拦截器准确探测数据周期为1 s。

建立如图1所示的博弈机动飞行场景模型。

图1 对抗作战场景示意图

如图1所示,任务场景可以描述为再入滑翔飞行器自M点出发,朝向目标点O进行俯冲段导引飞行。在无拦截器拦截情况下,其将沿M,M1,M2,O到达目标;在有拦截且自身不进行机动的情况下,其飞行经历时间tzk后至M1点,首次探测到位于T点的拦截器,之后拦截器经T1,T2,C1点命中目标,其中M2和T2点为两飞行器在碰撞前10 s的位置。为模拟并简化拦截器的指控系统,对拦截器的发射时间和初始位置、速度进行随机化建模。设M点在地面的投影点为M′。以O点为原点,OM′为X轴,垂直于X轴指向上为Y轴建立拦截器的发射坐标系。设T1点的坐标(XI0,YI0,ZI0)随机产生区域如图2所示,满足:

图2 拦截器初始位置分布

(7)

设拦截器在T1点时的速度大小为VI0,此时再入滑翔飞行器位于M1点的坐标为(XH0,YH0,ZH0),二者距离为r0。假设拦截器的速度指向为再入滑翔飞行器-拦截器连线方向,则可得拦截器速度方向为

(8)

式中:θI0和ψI0为初始弹道倾角和弹道偏角。

在机动飞行场景中,再入滑翔飞行器在M2点通过获取的态势信息进行首次机动,飞行一个决策步长时间后到达M3点,此时拦截器的导引弹道改变到达T3点。然后再入滑翔飞行器继续根据新的态势信息进行机动参数解算,依次飞过M4,M5等点。拦截器经过T4,T5等点后在C2点脱靶自毁,再入滑翔飞行器继续对目标点O导引。

考虑到再入滑翔飞行器在每个决策时刻对机动参数进行计算,则俯冲段机动问题可以被转化为一个序列决策问题:在一定的初始态势下,飞行器如何在连续的多个决策时间点输出机动参数。

其中,再入滑翔飞行器的场景(M点)随机变量有初始速度V0、初始路径角γ0、初始高度H0、射程RL;拦截器的场景(T1点)随机变量有首次被探测时间tzk、初始速度大小VI0、发射系下初始位置坐标(XI0,YI0,ZI0)和导引系数K。

2 俯冲段博弈机动问题的MDP模型转化

强化学习问题是建立在马尔科夫决策过程(Markov decision process,MDP)上的,MDP是一种通过交互式学习来实现目标的理论框架。实施决策及进行学习的主体(再入滑翔飞行器)被称为智能体,智能体之外所有与其相互作用的事物(拦截器、既定目标等)都被称为环境。这些事物持续进行交互,智能体选择动作,环境对动作做出相应响应,并向智能体呈现新的状态。环境也会产生一个奖励信号,即是智能体在动作选择过程中想要累积最大化的目标,交互过程如图3所示。

图3 马尔科夫决策过程中的交互

在每个离散时刻(再入滑翔飞行器俯冲段的决策步)t=0,1,2,3,…,智能体观测到所在环境状态的特征表达(或特征)St∈S,并且在此基础上选择一个动作At∈A(S)。下一时刻,作为其动作的结果,智能体接收到一个数值化的收益Rt∈R⊂R,并进入一个新的状态St+1。从而,智能体所处的MDP会给出如下序列:S0,A0,R1,S1,R2,S2,A2,R3,…,直到仿真交互结束。智能体的优化目标是最大化所获取的累积奖励G0：

(9)

式中:λ为折扣因子;Ri为第i步的奖励。

基于深度强化学习算法研究俯冲段博弈机动问题,首先需要对其马尔科夫决策过程进行建模,即选取和设计刻画俯冲段博弈机动决策过程的状态、动作和奖励规范。

1) 状态空间:强化学习的策略学习依赖于“状态”的概念,因为它既作为策略和价值函数的输入,同时又作为仿真模型的输入与输出。对于再入滑翔飞行器,状态变量应反映出其飞行状态与机动飞行任务,并尽可能降低数据维度、减少信息冗余。假设拦截器运动信息被有效探测,状态变量定义为

St=[Ht,RLt,Vt,σt,Δψt,HIt,RIt,VIt,σIt,ΔψIt]

(10)

式中:前5项依次代表再入滑翔飞行器在t时刻的高度、剩余航程、速度、路径角、航向角偏差,后5项依次为拦截器在t时刻的高度、已飞航程(相对O点)、速度、路径角、航向角偏差(相对O点)。

2) 动作空间:动作反映了控制变量对于模型状态的改变能力,是决策网络的输出值。

根据再入滑翔飞行器动力学方程,在飞行过程中,能够控制其每一时刻受力情况的是攻角和倾侧角。然而,直接将攻角、倾侧角的大小作为决策量有可能出现控制量突变的情况,将无法满足控制系统要求。因此选取攻角变化率和倾侧角变化率作为决策的动作变量,其大小范围可通过动作变量的归一化进行限幅控制。因此动作变量定义如下:

(11)

3) 奖励规范:实时奖励函数(收益信号)定义了强化学习问题中的目标,其设计准则应与俯冲段博弈机动目的(规避拦截器与到达目标点)对应。再入滑翔飞行器终止时刻落点偏差记为Lf,满足:

(12)

式中:RLf为仿真终止时刻的剩余航程;Hf为仿真终止时刻的高度。

设计连续的分段线性奖励函数如下:

RL=

(13)

(14)

式中:R为实际设计的总奖励函数;RL为与落点相关的奖励函数;L0为拦截器杀伤距离,根据经验取为10 m。当LZEM>L0时认为规避成功,此时总奖励由落点偏差决定。

由于规避威胁是一个需首先满足的强约束,故和脱靶量相关的奖励项呈现出如式(14)所示的二元形式。而由于落点偏差变化范围大,采取式(13)所示的连续形式奖励则利于策略根据梯度收敛。

3 基于改进PER-DDPG的博弈机动决策算法

如图4所示,首先给出传统DDPG算法的架构,然后基于优先经验回放(Prioritized experience replay,PER)[27]方法给出DDPG算法的改进项,最后给出基于改进的PER-DDPG算法对博弈机动策略网络进行训练的流程。

图4 算法实现框架

3.1 传统DDPG的算法架构

考虑到本文研究的再入滑翔飞行器俯冲段机动决策过程中,状态空间和动作空间连续变化,使用DDPG算法对机动参数决策求解具备天然优势。DDPG算法基于Actor-Critic(AC)架构,其核心是4个神经网络,分别是:在线决策(Actor)网络π(s|θπ),负责根据状态变量输出决策动作;在线评价(Critic)网络Q(s,a|θQ),负责对状态-动作值函数进行估计;目标决策网络π(s|θπ′),作为在线策略网络的学习目标;目标评价网络Q(s,a|θQ′),作为在线评价网络的学习目标。DDPG算法策略提升的本质是根据时序差分(TD)进行策略的学习训练。

在AC框架下,算法通过对“状态-动作”值函数Q(s,a)的估计优化实现对策略π的迭代更新。其中,Q(s,a)表征的是策略在当前状态s下采取动作a后能够获取的累积回报的期望值:

(15)

对于最优的Q(s,a),其满足如下贝尔曼方程:

(16)

相应地,状态值函数V(s)表征在当前状态s下按照策略π继续决策能获取的累积回报期望值:

V(st)=E[Gt|st]

(17)

依据确定性策略梯度,可对参数θπ更新如下:

(18)

3.2 基于优先经验回放方法的算法改进项

考虑到再入滑翔飞行器面临探索空间大、有效样本少的困难,基于PER方法对DDPG进行改进:

1)建立自适应动作噪声方法

传统DDPG算法在训练过程中使用一个OU噪声[25]对策略进行探索,但在实际应用中噪声参数需要根据训练效果进行调节,否则容易出现训练低收益阶段探索不足、高收益阶段利用不足的问题。为解决此问题,采取自适应方差的高斯噪声设计。定义最近任务成功率Srate为其在最近100个仿真回合中飞行任务成功的比率。建立均值为0的自适应高斯噪声Na～N(0,δ),方差δ随最近任务成功率变化:

δ=10-2×(1-Srate)

(19)

2)使用时序差分误差优先经验回放方法

在标准DDPG算法中,算法采用无差别采样方法对数据进行训练,这对于奖励信号丰富的任务能够较快收敛,但对于可行解稀少、奖励稀疏的任务,有效样本利用效率非常低而难以获取策略梯度,因此根据TD误差进行优先经验回放。对每个样本,计算TD误差如下:

ei=Ri+λQ′(Si+1,π′(Si+1|θπ′)|θQ′)-Q(Si,Ai|θQ)

(20)

当基础经验回放池填满之后,按照TD误差的绝对值对所有样本进行优先级计算:

pi=|ei|+ε

(21)

式中:pi为优先级;ε为一极小正值。

对基础经验池中的每条样本计算采样概率:

(22)

式中:υ表示使用优先级的程度,取为0.7[27]。

然而,若按照上述概率对回放池中的样本进行采样,将造成采样数据分布与实际仿真交互数据分布不一致,使得神经网络对数据的刻画具有一定偏差,从而无法完成最终的收敛任务。因此,需要采取重要性采样方法对不同采样概率的样本进行采样,第i个样本的重要性采样权重定义为

(23)

式中:N为经验池中的数据样本数量;β是调节权重的因子,取值范围为0～1,当其取1时表示对优先级采样概率进行完全修正,仿真中取为0.5[27]。

考虑重要性采样权重后,则Critic网络的损失函数的计算如下:

(24)

式中:NS为批量样本个数。

3)使用成功样本优先经验回放方法

除了采用TD优先经验回放方法外,考虑到策略探索前期成功样本极少、策略网络梯度难以产生有效梯度对策略进行改善,使用成功样本优先经验回放方法。即在策略网络训练的前期,构造一个成功样本经验库,维护100组成功样本。在对DDPG算法进行一步参数更新前,从成功样本库随机取出若干样本放到经验回放池。

4)对终端收敛性能进行局部调整。为保证DDPG算法在进行到任务较高成功率的训练后期仍具备较好的参数更新性能,使用修正的单轮训练方法。在训练前期,每回合对Actor网络进行更新的次数为Nupdate,在Srate>90%时调整为N′update=0.2Nupdate。

3.3 基于改进PER-DDPG的博弈机动算法步骤

基于改进PER-DDPG的算法步骤为

1) 使用随机参数θπ初始化Actor网络π(s|θπ),使用随机参数θQ初始化Critic网络Q(s,a|θQ);

2) 将在线网络参数拷贝给对应的目标网络,即θπ′←θπ,θQ′←θQ;

3) 初始化基础经验回放池RB(容量3000)和成功样本经验回放池RS(容量100);确定批量采样容量大小BS;

4) 对于每一次俯冲段博弈机动飞行仿真:

a. 初始化自适应探索噪声N的方差δ;

b. 初始化仿真交互环境,即对再入滑翔飞行器的初始射程、飞行高度、速度大小、飞行路径角进行随机,拦截器的首次被探测时间、初始位置、速度等进行随机,确定模型积分仿真时间步长tstep1=0.01 s和决策时间步长tstep2=2 s,获取到再入滑翔飞行器智能体的初始观测S0;

c. 对于每一个决策步长(t=0,1,2,…):

i)将观测的状态量输入策略网络再加上探索噪声得到当前决策动作输出:At=π(St|θπ)+Na;

ii)决策动作传递到仿真交互环境中,再入滑翔飞行器在当前飞行时刻tsim对决策动作At进行解析,得到每个积分步长下的当前攻角和当前倾侧角:

(25)

式中:αi和σi分别为当前积分步长的攻角和倾侧角,αi-1和σi-1为上一积分步长的攻角和倾侧角。

拦截器对再入滑翔飞行器进行导引飞行直至时刻tsim+tstep2或到达脱靶时刻(命中或脱靶);

智能体通过一个决策步长的仿真过程获取到新的状态St+1和即时奖励Rt;

iii)将元组存储到RB中。对每个经验样本,依据式(20)计算其TD误差。当基础经验回放池填满之后,依据式(21)计算样本优先级,依据式(22)计算采样概率,依据式(23)计算重要性权重。

d. 从经验池中采样学习(执行Nupdate次)

采取SumTree的形式对基础经验池中的样本进行BS次数据采样,获取到BS条训练数据。

采用均匀随机方法,从成功样本经验池中获取到SS条训练数据。令NS=BS+SS,则以上共得到NS个样本作为策略学习的数据。

ii)对NS个样本分别计算

yi=Ri+λQ′(Si+1,π′(Si+1|θπ′)|θQ′)

(26)

iii)计算NS个样本的平均损失函数

(27)

使用Adam优化器进行参数θQ的更新;

vii)计算Actor网络的平均策略梯度

(28)

使用Adam优化器进行参数θπ的更新;

viii)使用如下公式对目标网络参数软更新:

(29)

式中:τ为神经网络软更新系数,取为0.005;

e. 若再入滑翔飞行器完成对拦截器的机动且落点精度满足指标,此回合样本序列为成功样本,则将整回合状态转移元组存储到RS中;

f. 计算连续成功概率,根据式(19)更新δ。

4 仿真校验及结果分析

4.1 决策算法训练

仿真初始条件设置如下:

1)对抗场景初始运动参数范围。

2)神经网络结构以及超参数设置。参考经典DDPG确定两类神经网络的结构参数和超参数。

使用DDPG算法和改进PER-DDPG算法分别对俯冲段机动决策模型进行训练,训练过程的相关结果如图5和图6所示。

图5 平均累积回报值随回合数变化曲线

图6 最近100回合成功次数

从图5和图6可以看出,改进的PER-DDPG算法在训练到达2 631个仿真回合后收敛,在训练末期任务成功率稳定达到95%以上水平;相比而言,传统DDPG算法的收敛性较差,最高任务成功率不足70%。算法训练过程中,两个神经网络的损失函数变化曲线如图7和图8所示。

图7 Actor网络的损失函数

图8 Critic网络的损失函数

随着训练进行,Critic网络的损失函数逐渐降低,Actor网络的损失函数逐渐逼近最大期望回报的负值。在本文提出的动态噪声方差下,近100回合平均累积回报不断上升,策略的确得到了持续提升。直至训练收敛,近100回合成功次数由训练前的不足30跃升为95以上,说明算法实现了既定效果。

4.2 典型场景仿真校验

为了校验决策神经网络在典型场景中的有效性,根据表1范围进行参数随机生成如表3所示。表4给出了4种仿真场景下的统计结果。

表1 场景设置参数

表2 神经网络结构参数

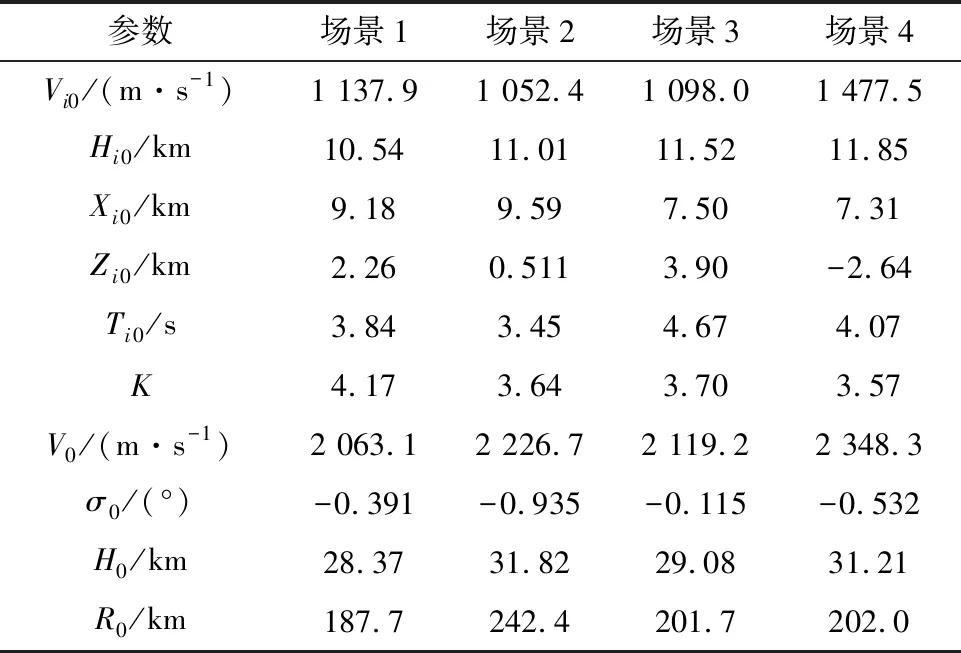
表3 4种场景下的初始参数

表4 不同场景的校验结果

从图9～图12可以看出,决策网络训练完成后,其输出的再入滑翔飞行器俯冲段博弈机动轨迹均可规避拦截器的拦截,且能够准确到达目标点;飞行路径角、攻角、倾侧角变化较为平滑,能够满足控制系统要求;飞行过程中的最大总过载也在其能力范围内(<20),这表明剖面机动轨迹设计能够满足飞行能力要求。从图13和图14可以看出,拦截器在飞行前期能够依据导引飞行锁定再入滑翔飞行器,但经过后者的多次机动后,拦截需用过载均在飞行末段达到可用过载阈值(20),导引弹道无法完成对再入滑翔飞行器的拦截。

图9 拦截器发射系X-Z平面对抗弹道

图10 拦截器发射系X-Y平面对抗弹道

图11 再入滑翔飞行器的法向过载随时间变化曲线

图12 再入滑翔飞行器的横向过载随时间变化曲线

图13 拦截器的法向过载随时间变化曲线

图14 拦截器的横向过载随时间变化曲线

综上,在校验的4个场景中,决策网络可以完成机动飞行任务。

4.3 统计校验与泛化性评估

使用深度强化学习方法进行智能在线决策的优势在于将在线计算压力转移到离线训练中。在线使用时,弹载计算机只需在每个制导决策周期将观测的状态量数组输入给决策神经网络,即可得到机动参数,从而实现智能博弈机动,完成既定任务。

为对决策网络有效性进行评估,开展统计校验。使用表1所示范围的场景参数进行1000次仿真校验。计算平台CPU为Intel(R) Core(TM) i7-8700U,内存8 GB,决策网络每1 000次的调用时间为0.361～0.403 s,平均单次调用时间小于0.5 ms,具备较好的实时性。经统计,同时满足再入滑翔飞行器落点偏差小于10 m且拦截器脱靶量大于10 m的样本个数为927,即说明决策网络输出的策略成功率大于90%。仿真校验的脱靶量分布结果如图15所示。

图15 拦截器脱靶量样本分布

仿真校验的落点偏差分布结果如图16所示。

图16 落点偏差样本分布

针对拦截器的未知特性,对场景初始参数进行调整,得到决策网络在拦截器不同未知特性下的结果如表5所示。

表5 拦截器未知特性下的校验结果

从校验结果可知,决策神经网络具备较好的泛化能力,在拦截器不同未知特性下仍能保持较高的任务成功率,相较于训练过程末期的任务成功率最高降低不到5%,表明所提出的智能博弈机动策略对未知参数的抗干扰能力较强。

5 结 论

面向再入滑翔飞行器,针对其俯冲段博弈机动问题进行深入研究,取得以下成果:首先,将俯冲段博弈机动问题建模为马尔科夫决策过程,定义了状态、动作与奖励函数;然后,针对传统DDPG算法进行改进,对经验回放机制和探索噪声设计进行优化,提出了基于改进PER-DDPG的俯冲段博弈机动决策算法,提高了训练初期的寻优能力和后期的收敛性能。最后,在多场景飞行仿真校验和大规模泛化能力校验中,统计数据验证了决策算法在进行机动决策上的有效性。针对不同场景,算法具备较强的泛化性,可为再入滑翔飞行器的俯冲段智能博弈机动飞行提供参考。