绳系库仑结构姿态波动控制方法
石安睿,张景瑞,蔡 晗
(北京理工大学宇航学院,北京 100081)
0 引 言
随着人类空间活动的不断增加,空间任务需求也愈发多样和复杂,以至于单个卫星有时难以实现任务目标[1]。同时,随着在轨航天器及空间碎片的不断增多,例如地球同步轨道等有限的重要轨道资源需要被更高效的利用。因此,可以满足多样任务需要、提高轨道资源利用率的卫星编队结构被逐渐提出和研究[2]。由于通过持续轨道控制保持构型的传统卫星编队会产生更多燃料消耗和控制需求,因此利用系绳拉力辅助编队构型保持的绳系卫星编队逐渐受到关注[3-4]。
为实现10~100 m距离编队的精确控制,采用库仑力维持编队构型的库仑编队[5]以及利用库仑力构造虚拟系绳的库仑力绳编队[6]概念被提出和研究。同时,由于德拜屏蔽效应的存在,利用库仑力的卫星编队主要被应用于地球同步轨道和深空航天器编队控制中[7]。
为了得到更好的编队构型稳定特性,Seubert等[8]提出同时引入系绳和库仑力的绳系库仑结构(TCS),该结构利用库仑力在航天器之间产生排斥力的同时通过柔性系绳连接各航天器以保持构型稳定。Seubert等[9-10]针对绳系库仑结构的动力学特性、稳定性等进行了分析和研究。在此基础上,Qi等[11]和Zhang等[12]分别提出了更加复杂的绳系库仑双金字塔编队和绳系库仑金字塔离轨编队并都对动力学和平衡构型下所需的电荷量进行了求解分析。但是在现阶段,对于绳系库仑结构的控制问题依然少有研究。
绳系库仑结构不仅具有明显的柔性结构,还由于其构型的特殊性,又具有刚性结构的部分特点[13]。与之相对地,对连续体进行波动分析时,宏观上的连续体单元可以具有明显的刚性特点,但同时其振动、形变又体现了部分柔性特点。因此,基于波动思想对绳系库仑结构进行控制较为可行。
Flotow等[14]首先基于波动思想提出了行波控制的概念,给出了以状态参量为变量的波动状态空间方程。Saigo等[15]提出了在时域上的基于波吸收的振动控制方法,得到了很好的控制效果。O’Connor等[16]在时域上利用达朗贝尔行波解分析波动方程并基于回波吸收思想,提出了一种吊车运动的控制方法,通过控制吊车速度实现对绳索中反射回波的吸收,抑制末端质量块在运动过程中产生的振动。Qi等[17]基于Connor等提出的方法设计了目标残余液体燃料的绳系拖曳系统的摆动反馈控制器。
事实上,达朗贝尔行波解主要针对无限(半无限)长弦的波动方程。因此在波动分析时,对不同边界条件下有限长弦的运动方程进行更加完善直观的分析和研究具有重要的理论和工程实际意义。
本文提出使用吊环模型作为高度简化的物理模型,以反映弦的运动及其物理意义,并通过对吊环模型建立并求解其不同边界约束下的运动方程,明确描述了波在吊环模型中的传播和作用规律,并且基于吊环模型的波动分析以及回波吸收思想,针对库仑绳系结构,设计了波动控制器,实现了对其的姿态控制。
本文结构如下:在第1节中,针对吊环模型建立了波动方程描述其运动,基于有限长弦的波动方程在不同边界条件下的解对吊环模型运动进行了分析,得到了波在系统中的传播和作用规律。在第2节中,运用拉格朗日方程建立了库仑绳系结构的动力学方程,并基于回波吸收思想设计了库仑绳系结构姿态波动控制器,并进行了仿真和分析。第3节对本文的研究进行了总结。
1 吊环模型运动分析
1.1 吊环模型
本文使用吊环模型作为物理模型,描述由柔性结构连接的摆动系统。
吊环模型由平面内分别套在两根平行的光滑直杆上的吊环1和吊环2以及连接两个吊环的始终张紧的弦组成,如图1所示。吊环可被视作质点,将吊环1在杆上的初始位置作为坐标原点,则坐标系X轴沿弦线方向垂直于直杆;Y轴沿直杆方向向上。
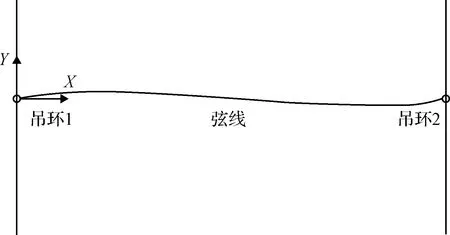
图1 吊环模型
尽管弦始终张紧,但是弦线并非一定处于一条直线上,因此在假设均质的始终张紧的弦沿Y轴摆动较小的情况下,弦的运动可以通过一维波动方程描述为
(1)
式中:常数ρ为弦的线密度;T为弦张力,张力变化较小时可以假设T为常数;f是分布在弦上的外界激励。在不同情况下,波动方程受到不同的边界条件约束和初始条件的约束。
1.2 不同边界条件下的吊环模型运动分析
在不同物理情况下,由于边界条件存在差异,因此波动方程解的形式也不尽相同,与之相对应地,弦的振动和波的传播形式也有所不同。为了更好地反映模型在外激励作用下的运动特性,在本节设定吊环1受力控制,对两种典型的物理情况所对应的不同边界条件下的吊环模型运动进行分析。考虑到弦的运动方程的基本假设,弦上任一点只沿Y轴方向运动,因此如无特殊说明,本节所提及的位移和速度都是特指在Y轴方向上的位移和速度。此外,考虑到吊环质量造成的影响,当吊环材质和弦线相同时,可以将吊环看作是弦线的一部分“延长”,因此在分析弦线运动时如无特殊说明,认为吊环材质和弦线相同。
情况1. 吊环2自由
(2)


(3)
此时,问题由时域偏微分方程转化为了频域常微分方程。求解式(3)可得其特解为
(4)
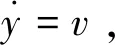
(5)
值得注意的是,通过此方法会使问题失去初始状态信息,因此问题本质被转变为在相应外激励下,弦所产生的位移改变响应,而非实际位移,但是这并不妨碍对弦的运动进行分析;并且为便于表述,不妨设模型任一位置初始的位移、速度均为0。
因为f0=f0(t)u(t)(u(t)为阶跃函数),则对于任意t=τ+m×2l/c(0≤τ<2l/c,m∈N),式(5)可以被等价变化为
(6)
显然,观察式(6)可以发现,随着时间的增加,力波会不断在模型中传播,且在到达模型一端后会发生反射并继续传播。故模型任一位置处的速度响应是在其上所受的所有力波的叠加作用引起的。此外,对式(6)分别取x=0和x=l可得吊环1和吊环2的运动规律,可以发现,在外激励持续作用下,二者的速度交替增加,因此模型会产生振动。
情况2. 吊环2自由但质量较大
(7)
式中:l为两直杆之间的距离;φ和ψ分别为弦的初始和速度;m为吊环2的质量;f0为吊环1所受的控制力。对式(7)做傅里叶变换,则可得:
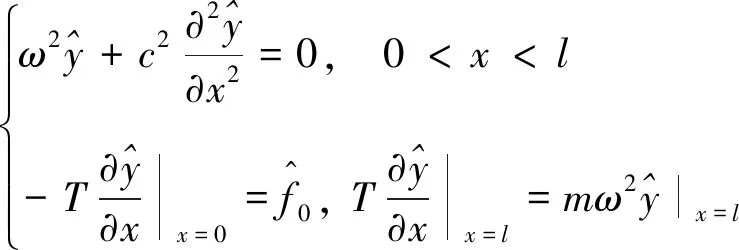
(8)
此时,问题由时域偏微分方程转化为频域常微分方程。求解式(8)可得其特解为
(9)
将式(9)进行等价变换后再进行傅里叶逆变换,并以t-l/c代换t可得:
(10)
式(10)较为复杂,难以将其整理为类似式(6)的形式。因此,对吊环2单独进行分析。当x=l时,式(10)将化为描述吊环2运动的方程:
(11)

(12)
由于吊环1与弦线的材质相同,且弦线阻抗大小为T/c,因此吊环1在受到激励力f0时可以等效于受到速度激励v0=cf0/T。因此,式(12)的解,即吊环2的速度可写作:
vl(t)=
(13)

基于以上分析可知,在受到激励作用时,吊环1将加速至v0,并将波传播出去,吊环2受到波的作用将吸收部分波,加速并逐渐趋近2v0,同时反射剩余部分的波,之后吊环1将同时受到反射波和激励作用。在激励不断作用下的情况下,波将不断在模型中产生和传播使吊环1和吊环2将交替加速,引发模型振动。
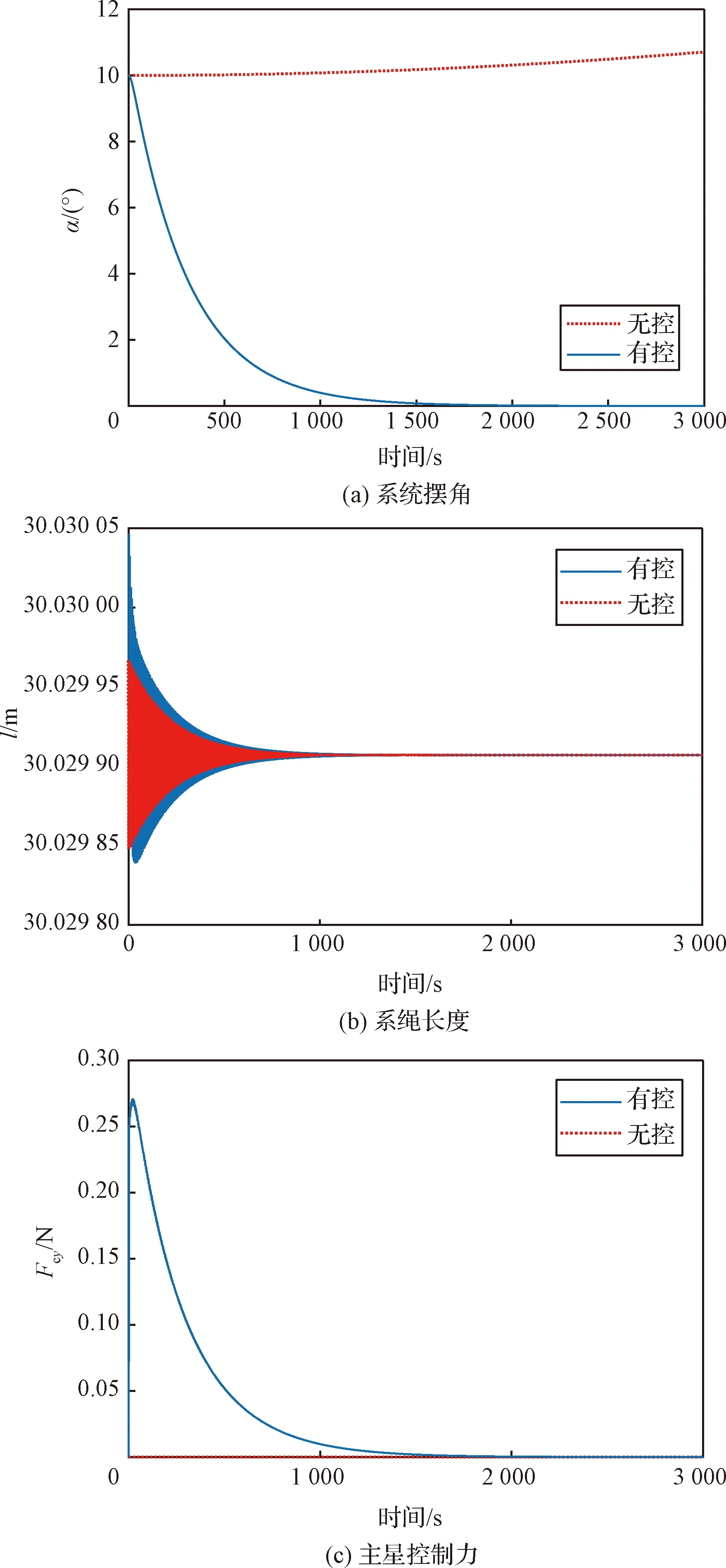
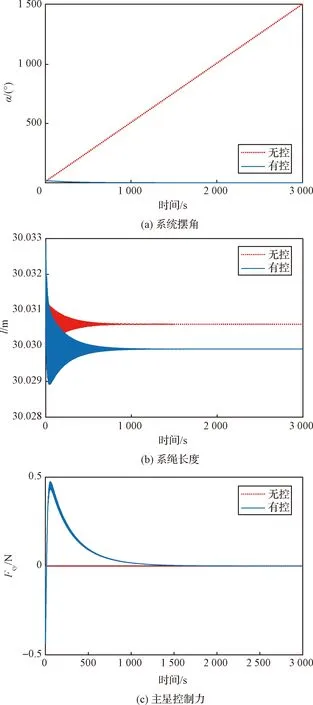
因此模型中除吊环2外任意位置xx(0≤xx vx(t)= (14) 对于绳系库仑系统,一般由可以提供控制力并且带电荷的主星、带电荷的副星以及连接两者的系绳组成,且主副星的电荷正负性相同以提供斥力。 假设地球为均质球体,完全中心引力场,系统在轨道面内运动且轨道近似圆轨道,主星和副星视作质点,系绳是可伸长的半弹簧。 定义轨道系如图2所示,以系统质心为原点,Yo轴与地心和系统质心连线平行并指向远离地心方向,Xo轴在轨道平面内且与Yo轴垂直。并且如图2所示,系绳在轨道面上的投影与Yo轴的夹角α以及主星与副星之间的距离l被选为广义坐标。认为系绳实际绳长为l。考虑到轨道接近圆轨道,则系统动能可表示为 图2 广义坐标定义 (15) Ω2l2(-3sin2α+1) (16) 系统的弹性势能可以写作: (17) 式中:kt是系绳的刚度系数;lnom是系绳原长,并且在实际绳长小于原长时,系绳拉力为0,对应弹性势能也为0。系统的电势能可以写作: (18) 式中:kc是库仑常数;qm和qs分别为主星和副星所带的电荷量,且二者正负性应相同。系统中各广义坐标对应的广义阻尼力分别可以写作: (19) 式中:Fcx和Fcy分别是主星在Xo轴和Yo轴的推力分量;ct是系绳的阻尼系数,且在实际绳长小于原长时,阻尼系数也为0。系统的动力学方程通过拉格朗日方程可以写为 (20) 式中:Θ∈{α,l}。将式(15)~(19)代入式(20),可以得到系统的动力学方程: (21) 系统姿态控制问题即是将系统从一种角度/角速度状态转换至另一种角度/角速度状态。从这一角度而言,系统的姿态控制问题可以被视作对于系统具有“初始摆动”的控制问题。 通过吊环模型的分析可知,模型摆动由波在模型内上不断传播所引发。因此,若可抵消传播至受控吊环1处的波,模型的摆动现象会得到抑制。并且由于绳系库仑系统中库仑力的存在,当系统受到控制或扰动时,两星之间的相对距离变化较小,因此在系统姿态变化时,可以近似看作吊环模型受到激励而变化的情况。 基于这一思想,若将主星和副星分别看作吊环1和吊环2,将系绳看作弦线,并且在初始时刻前已有速度激励v0由主星输入系统,则问题可以转化为1.2小节的情况2。因此,通过吸收持续影响系统的等效输入激励v0所产生的波,可以实现系统的摆动抑制即完成系统的姿态控制。根据式(12),可以得到t-l/c时刻的等效输入激励: (22) 因此通过副星的状态即可得到等效输入激励。此外,尽管将系绳看作张紧的弦时,系绳几乎不会是直的,但宏观上观察系绳摆动时,将系绳近似看作直线。因此,副星的运动满足: (23) 将式(23)代入式(22),此时可以通过易于获得的信息得到等效输入激励: (24) 因此,可以通过t时刻副星的运动状态获得t-l/c时刻等效激励,并且等效激励产生的波将在t+l/c时刻传播至主星处,为抵消传播至主星的波,t+l/c时刻主星的控制速度满足: (25) 将式(25)中的t以t-l/c代换,可得主星的控制速度vc的表达式: (26) 在考虑主星执行机构为推力器的情况下,在已知主星速度vm的情况下,主星应输出的控制力可由比例控制得到: Fcy(t)=kp[vc(t)-vm(t)] (27) 为验证所设计的绳系库仑结构姿态控制器的控制效果,进行仿真校验。仿真所用的参数如表1所示。 表1 仿真参数 针对不同场景,设定以下两种不同的仿真初始状态进行仿真校验: 工况 1的仿真结果如图3所示,其中图3(a)、(b)和(c)分别给出了绳系库仑结构在受控和不受控情况下的姿态角变化、绳长变化以及输出的控制力大小。通过图3(a)可以发现,在无控情况下,系统姿态逐渐发散,这是重力梯度影响使系统倾斜时有向当地铅锤方向变化的趋势;系统有控时的姿态角持续减小,在1 500 s附近收敛,且这一过程中没有摆动现象。由图3(b)可知,在系统受控情况下,系绳始终张紧,且最终稳定在30.03 m附近。此时系绳张力和主副星之间的库仑斥力相平衡;无控情况下,尽管系统姿态逐渐发散,但在仿真时段内系绳径向受力与稳定状态相近,因此绳长也保持在30.03 m附近。图3(c)显示,在姿态角的稳定控制过程中,主星输出的控制力大小最大不超过0.3 N。 图3 系统有初始姿态角的情况 工况 2的仿真结果如图4所示。观察图4(a)可知,无控情况下系统由于存在初始姿态角速度而发生转动,因此姿态角不断积累并且大小几乎与时间成线性相关;在系统受控时,其姿态角在经历短暂时间的增加后持续减小,并在1 500 s附近收敛。图4(b)显示,在系统受控时,系绳始终保持张紧且最终稳定在30.03 m附近;无控情况下,绳长稳定在比系统受控稳定状况下稍长的状态,这是由于系统的旋转对系绳提出了更多的张力需求。图4(c)中,在实现姿态角的稳定控制整个过程中,主星输出的控制力大小最大不超过0.5 N。 图4 系统有初始姿态角和角速度的情况 综合对比两种控制情况仿真可以发现,控制器对绳系库仑结构的姿态角和角速度控制都有良好的效果。控制力最值输出与初始姿态角和角速度成明显的线性关系,这一点也可以从控制律表达式中推测得到。因此,在对绳系库仑结构进行分析设计时,可以根据系统初始姿态对所需的控制力最值进行估计。 本文利用两种边界条件下的波动方程对所提出的吊环模型的运动以及波在其中的传播情况进行了分析。将绳系库仑结构的姿态控制问题转化为摆动控制问题,并基于回波吸收思想,设计了反馈控制器以实现绳系库仑结构的姿态控制。通过仿真校验了所设计控制器的控制效果,发现无论是进行绳系库仑结构姿态角调整抑或是同时对绳系库仑结构进行转动抑制,控制器都可以在不产生额外的摆动的情况下较快地实现绳系库仑结构姿态控制,并且对于控制力的需求很小,易于工程实践。 本文针对绳系库仑结构这一空间大型柔性结构所设计的欠驱动控制器,在只需对绳系库仑结构的主星进行运动控制的情况下,即可实现系统整体的姿态控制,且对控制输出要求较低。因此,从控制需求和控制冗余角度而言,所设计的控制器对绳系库仑结构的姿态控制具有较高的实用性和可靠性。2 绳系库仑结构摆动控制
2.1 绳系库仑系统动力学


2.2 绳系库仑系统姿态控制器设计
3 仿真校验
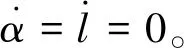
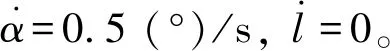
4 结 论

