基于流量分配优化的天然气管网模拟计算方法

林 敏

(中国石油化工股份有限公司天然气榆济管道分公司)

0 引 言

我国已成为天然气市场的主要国家，截至2022年底，我国已成为天然气进口大国。天然气燃烧产生的热值是其价值的主要标志，相同体积不同气源的天然气燃烧产生的热值差别很大，而我国天然气的体积热值最小为33.9 MJ/m3，最大为45 MJ/m3，因此不同热值的天然气以同样的体积价格进行交易是不合理的。我国天然气计量、计价和贸易交接仍以体积计量为主，在管网互联互通、气质复杂多元的情况下，体积计量已不适应目前天然气行业发展的需要。为此，国家相关部门和天然气生产、输送及销售企业均在努力推进天然气能量计量方式的实施。

在能量计量模式下，根据GB/T 22723—2008《天然气能量的测定》[1]，精确地模拟天热气管网中气体的流动状态，是节约设备投资和计量站现场改造、施工费用的必要前提。同时GB/T 18603—2014《天然气计量系统技术要求》中也规定了B级和C级计量站需要采用赋值方式获取组成和发热量数据的要求[2]。

本文将水力方程、能量方程、组分守恒方程及真实气体状态方程耦合，结合流量分配算法、组分混合算法，计算天然气在管道中任意位置的流动参数与气质组成，依据GB/T 11062—2020《天然气发热量、密度、相对密度和沃泊指数的计算方法》，实现标准状态下天然气发热量的精确计算[3]，以期为能量计量的实施提供帮助，节约设备投资和计量站改造费用。

1 算法与数学模型

天然气在管网内的流动状态模拟以水力计算为基础，通过求解水力方程组获得管道内气体的压力和流速，使用能量守恒方程和状态方程求解管道内气体的密度及温度，依据组分输运方程求解天然气组成，结合流量分配与组分混合算法，计算天然气的发热量。

1.1 控制方程组

天然气流动状态水力方程组包含连续性方程和动量守恒方程：

(1)

能量守恒方程为：

(2)

式中：ρ为密度，kg/m3；ω为流速，m/s；t为时间步长，s；x为空间步长，m；p为压力，Pa；g为重力加速度，m/s2；θ为管道倾角，rad；λ为管道摩擦因数；D为管道内径，m；A为管道截面积，m2；T为管内天然气温度，K；h为焓，J；T0为环境温度，K；K为综合换热系数，W/(m2·K)。

方程(1)中的管道摩擦因数λ由 Colebrook-White 方程计算[4]，其表达式如下：

(3)

式中：e为管壁表面粗糙度，m；Re为雷诺数。

在天然气运输过程中，常有多个气源混合的情况，混合后天然气管网中的气质组成情况可通过数值计算方法获得，计算过程中需要耦合组分输运方程：

(4)

式中：c为摩尔分数；Dx为轴向扩散系数，m2/s；Dr为径向扩散系数，m2/s；r为半径，m；Rc为源项，s-1。

在求解过程中，首先根据水力方程、能量守恒方程和GERG-2008 方程迭代计算出天然气流动参数；然后利用组分输运方程求解管道组分变化，并更新热力学参数，求解节点的发热量。

由于轴向扩散损失和径向扩散损失相较于整个管网系统的损失较小，在计算时将扩散项和源项忽略，以节省计算资源，提升计算效率。此时组分输运方程为[5-6]：

(5)

因为计算介质为天然气，所以需要考虑气体状态方程才能使求解方程组封闭。在ISO标准和技术应用中，AGA-8 和 GERG-2008是2种常用的计算方程[7]。其中，GERG-2008方程是德国波鸿大学热力学研究所提出，适用于求解天然气和其他混合物在较宽压力范围内的体积性质和热性质，改善了AGA-8方程对混合气体性质的计算性能[8-10]。GERG-2008 方程可以通过无量纲亥姆霍兹自由能及其导数显式表达天然气的所有热力学性质，天然气的亥姆霍兹自由能计算与组分有关[11]。可以使用无量纲亥姆霍兹自由能及其导数简化模拟方程组，并耦合气体组分输运方程实现天然气流动速度、气体流量分配及气体组分混合结果的精确模拟。亥姆霍兹自由能公式如下：

(6)

无量纲亥姆霍兹自由能可以表示为：

(7)

(8)

ρr和Tr是混合物无量纲密度和无量纲温度的函数，只取决于混合物的摩尔组成。对于能量守恒方程，使用无量纲亥姆霍兹自由能对内能和焓进行替换并进行处理，得到：

(9)

方程(9)中，无量纲亥姆霍兹自由能α的上标r表示剩余无量纲亥姆霍兹自由能，下标δ、τ表示无量纲亥姆霍兹自由能对无量纲密度及无量纲时间的偏导数。

由于无量纲亥姆霍兹自由能及其偏导数仅是气体密度(无量纲密度)、温度(无量纲温度)及组分的函数，且无量纲亥姆霍兹自由能及其导数在上述方程中显式表达，即在已知气质组成的情况下可以根据初始条件直接计算。所以采用GERG-2008方程作为状态方程时，不仅提升了混合气体性质的计算性能，还减少了不必要的微分或积分表达式。由上述分析可知，能量守恒方程可以表示为无量纲密度、无量纲温度、天然气流速和无量纲亥姆霍兹自由能及其偏导数的函数。

天然气管网中气体的流动状态实时变化，但单一管道的材料、状态及使用年限等可以认为一致。对于长输管道来说，管道长度足够长，且管段曲率半径远大于直径，因此，天然气在管道中的流动可以视为一维非稳态流动，管道的离散结构如图1所示。采用如图2所示的分段线性型线作为函数及其导数对时间及空间的局部型线，对守恒型方程组积分，得到离散后的控制方程，如式(10)所示。

图1 管网空间离散示意图Fig.1 Schematic diagram of spatial discretization of the pipeline network

图2 分段线性型线Fig.2 Segmented linear lines

采用基于压力的有限体积法进行计算，计算流程如图3所示。

图3 计算流程图Fig.3 Calculation workflow

(10)

1.2 流量分配算法

在流量分配过程中，由于管道连接点处天然气流动状态和损失的复杂性，难以通过控制方程准确求解下游管道初始参数。在实际工况下，下游管道往往安装压力和温度计量设备。所以可以在将仪表测量值作为限制条件的前提下，假设下游管道初始压力、温度和流速，进行迭代求解。这个过程可以视为多目标优化问题，其中决策变量为下游管道初始压力、温度、流速，优化目标如下：

(11)

式中：e1、e2为误差；p为初始压力，Pa；T为温度，K；下标c代表计算值；下标r代表实际值。且2个误差均小于相应的误差要求；限制条件则需要对整个天然气流动模拟过程进行处理分析。

在优化过程中，需要多次使用前文章模型进行计算，这会耗费大量时间。代理模型可以将通过模拟获得的样本点进行拟合，从而得到每个目标函数与输入变量间的近似预测模型，无需进行大量的数值求解工作[12]。本文通过抽样方法选取样本点后，建立Kriging代理预测模型，使用NSGA-Ⅱ遗传算法进行优化求解。

Kriging代理模型的建立需要在初始参数组成的样本空间内进行抽样，拉丁超立方抽样(LHS)方法是一种随机多维分层抽样方法，根据初始参数的取值范围，将样本空间等分为N个相互独立的子区域，并在每个子区域中进行等概率抽样，得到具有良好空间均匀性和填充性的样本集，因此本文采用LHS方法进行抽样操作。

为了满足Kriging代理模型的计算精度，初始样本的数量不少于决策变量的10倍，本文流量分配优化的决策变量为3个，为保证代理模型的通用性，环境温度也应作为初始变量，因此初始样本点的数量设计为50个[13-14]。

在代理模型建成后，采用R2误差分析法验证代理模型精度。R2误差分析法反映了预测值与实测值的偏差程度，R2越接近1，代理预测模型的全局近似精度越高。其计算方法如下：

(12)

NSGA-Ⅱ作为一种采用快速非支配排序过程、精英保留策略的排序遗传算法，与传统遗传算法相比，其算法运行效率高，收敛速度快，适用于3个及以下的多个目标优化设计[15]。其主要计算流程为[16]：

(1)随机产生个体数为N的初始种群Fg，按照非支配关系排序后进行交叉、变异操作，产生子代种群Sg。

(2)将父代种群Fg与子代种群Sg混合，按照非支配关系排序后从最优个体开始，选取N个个体组成新的初始种群Fg+1。

(3)对种群Fg+1进行交叉、变异操作后，重复流程(1)和(2)过程，直到达到迭代步数。

基于上述方法，可以在最终进化结果中，构建出满足下式的 Pareto前沿：

(13)

对Pareto前沿中的非劣解的目标函数值归一化，选取距离理想结果最近的非劣解作为最优解[17]。

优化设计得到结果的优劣很大程度上取决于代理模型的预测精度，合理的加点准则可以提高模型精度。把最优解对应的决策变量代入控制方程进行模拟计算，将获得的模拟结果与温度计、压力表示值进行对比，若误差大于规定，说明代理模型在该决策变量取值下的预测结果不满足要求。此时，将该点加入初始样本点对代理模型进行更新，重新进行优化计算，直到误差满足要求。将优化结果作为初始条件，利用边界条件随时间的变化规律，使用控制方程迭代计算每个时刻管道各处的参数，然后根据计算误差来确定是否需要做修正。流量分配计算流程如图4所示。

图4 流量分配计算流程图Fig.4 Workflow of flow distribution calculation

1.3 组分混合算法

在天然气管网结构中，往往会有多个天然气气源。当不同气源的天然气汇集到同一管道时，需要对混合后的天然气气质重新进行分析。FAN D.等[18]提出了一种管网结点结构的特殊处理方法，即将动量方程单独进行离散，其结点离散方式如图5所示。

图5 结点单元示意图Fig.5 Schematic diagram of node elements

如图5a所示，动量方程在动量控制体进行离散，其余方程在图5b所示的质量控制体内离散。其中，在质量控制体进行离散的方程均可用输运方程的形式表达。

对于整个结点结构，其控制方程组可以表示为如下形式：

(14)

通过求解控制方程组(14)，可以获得不同管道天然气混合后的组分、压力、流量及密度等参数。需要注意的是：天然气管道长度较长，混合气体在相对较短的距离内达到均匀状态，所以这里没有考虑气体混合后的均匀性问题。

天然气管网各处气体组分含量已知后，使用ISO 20762—2中的方法对压缩因子、声速进行计算。依据 GB/T 11062—2020 中的方法计算发热量和沃泊指数。

2 工程实例对比分析

基于前文所述计算方法，编制了计算程序，分别对流量分配、组分追踪和发热量进行求解。以山东管网系统中3个计量站的实际运营数据进行验证，其结构示意如图6所示。

图6 计量站示意图Fig.6 Schematic diagram of the measuring station

在12：00-21：00，计量站A作为输气站，计量站B、C作为储气站，此时可以用来验证流量分配计算模型。在1：00-10：00，计量站B、C作为输气站，计量站A作为储气站，此时可以用来验证组分混合模型。管道的参数如表1所示。

表1 管道尺寸参数Table 1 Pipeline dimensions

2.1 控制方程组验证

选择图6计量站A中的直管道对控制方程的计算精度进行验证。管道的长度为1 500 m，内径为585 mm。6个时刻的计算结果如表2所示，计算误差如图7所示。

表2 不同时刻参数Table 2 Parameters at different time

图7 控制方程组计算误差Fig.7 Calculation errors of governing equations

由图7可以看出，使用控制方程组(式(10))计算得到的温度最大差值为0.22 ℃，压力最大误差为0.17%，工况流量最大误差为0.33%，均满足GB/T 18603—2014对A级计量站的计量要求。

2.2 流量分配算法验证

各计量站不同时刻的参数值如图8所示，在这段时间内，气质不发生变化。

图8 不同时刻计量站计量数据Fig.8 Measuring data of the measuring stations at different time

以管道2为例，使用遗传算法进行流量分配计算。首先，依据计量站B的历史运营数据确定代理模型各物理量的取值范围，采用LHS方法抽取50组初始样本。将样本分别代入第1章中的计算模型，利用计算结果分别构建仪表测点压力、温度的Kriging代理模型。获得代理模型后，另取10组初始值进行验证。经验证，R2值分别为0.97和0.95，说明该代理模型计算精度足够高。

使用NSGA—Ⅱ遗传算法进行优化求解，其中，种群数设为200，变异率为0.1，交叉率为0.9，最大迭代次数设为500。管道2的初始压力、温度及流速的取值范围如下：

0.95pb≤p0≤1.05pb

(15)

0.95Tb≤T0≤1.05Tb

(16)

0.95ωc≤ω0≤1.05ωc

(17)

式中：下标b代表管道1末端的物理量；下标0代表管道2初始时刻的物理量；ωc为以管道1末端温度、压力作为管道2初始值，使用二分法计算得到初始流速的估计值。管道2初始时刻的取值范围如表3所示。

表3 管道2初始参数取值范围Table 3 Ranges of initial parameters of Pipeline No.2

由于目标优化的最终结果是压力、温度误差取最小，所以只要Pareto最优解满足式(13)，就可以认为对应的决策变量为最优。利用第一个时刻的决策变量最优值，计算后续时刻计量仪表安置点的结果，误差如图9所示。

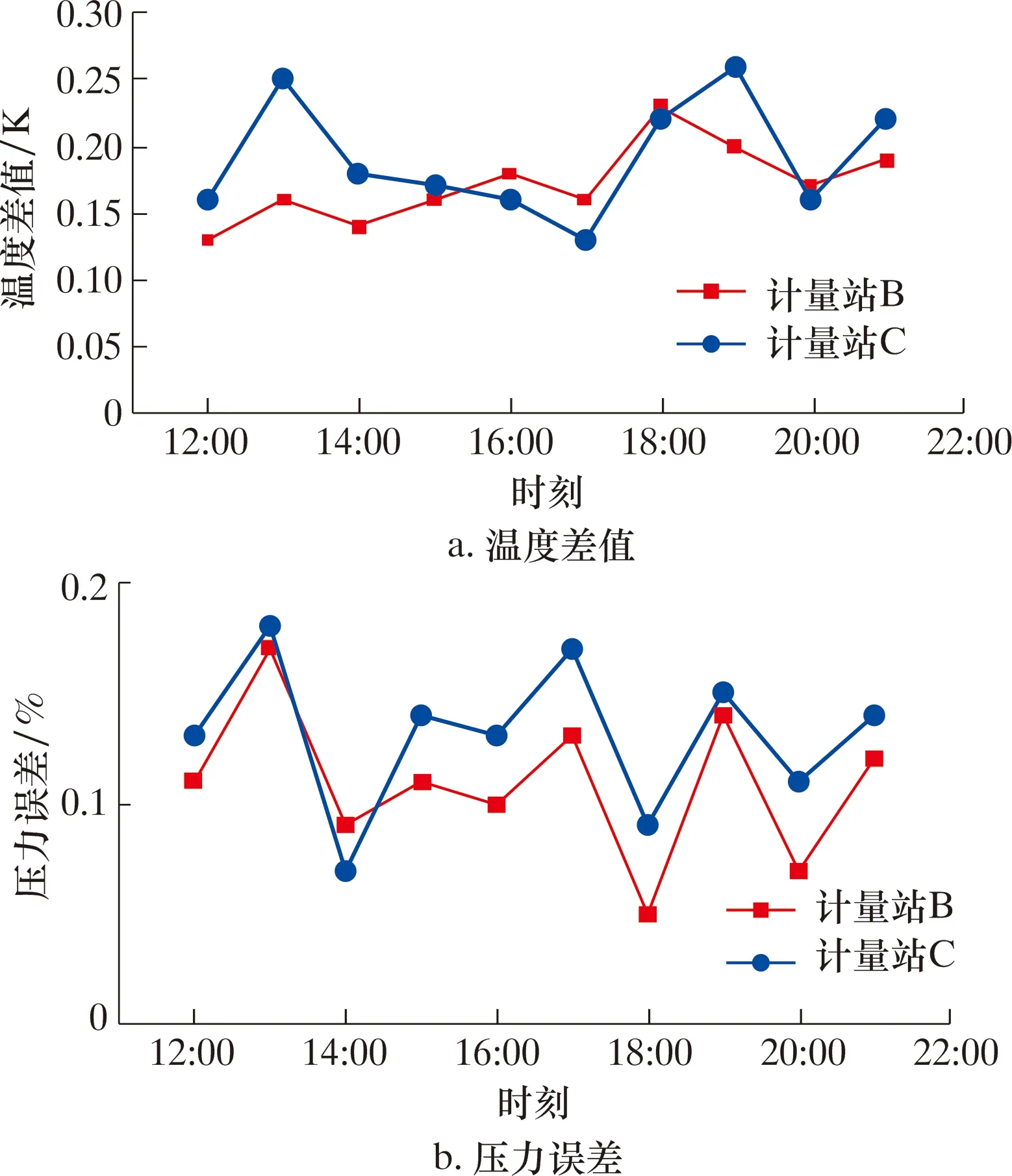
图9 计算误差图Fig.9 Calculation errors

由图9可知，最大温度差值为0.26 K，最大压力误差为0.19%，满足标准要求，证明该算法可以精确计算流量分配模型。需要注意的是：如果上游管道参数发生较大变化，模拟计算结果不一定满足精度要求，此时会重新抽样进行遗传算法计算，从而保证每个时刻的模拟结果在误差范围内。

2.3 气质组成和发热量计算验证

在1：00-10：00，计量站B、C作为输气站，计量站A作为储气站。此时，管道2、3有着不同的气质组成，天然气在管道1发生组分混合。

表4为不同时刻各计量站天然气中CH4的实际摩尔分数。

表4 不同时刻各计量站CH4摩尔分数Table 4 CH4 molar fraction of each measuring station at different time

图10为计量站B、C中除CH4外天然气各主要组分实际摩尔分数。从表4和图10中可以看出，随着时间的变化，不同气源的天然气气质组成会发生无规律波动。这是因为天然气在开采时气质组成会发生波动，同时在天然气管网系统的工作过程中，管道中天然气流向的改变、阀门的启闭等也会对管道中的气质组成造成影响。

图10 不同时刻计量站B、C各组分摩尔分数Fig.10 Molar fractions of each component in the measuring stations B and C at different time

使用前文所述方法，根据现场实际数据，将模拟计算的时间步长取为1 h，进行气质跟踪模拟计算。图11为计量站A 中天然气主成分(甲烷、乙烷、丙烷)及其他成分的计量与模拟数据。

图11 不同时刻计量站A各组分摩尔分数模拟值与计量值Fig.11 Simulated and measured molar fractions of each component in the measuring station A at different time

由图11可以看出：甲烷含量在5：00、6：00时发生较大波动，计量误差在5：00时达到最大，为0.178%，其余时刻的计量误差在0.1%以下；乙烷和丙烷含量在5：00时也发生了明显的变化，这是因为该时刻计量站C中天然气正庚烷含量发生了较大变化，计量站B、C中乙烷含量也有波动；乙烷含量在1：00、2：00时发生较大变化，计量误差在2：00时达到最大，为0.698%，这是因为在1：00、2：00时，计量站C中乙烷含量波动变大；除乙烷外气体成分在7：00、8：00时刻均发生了波动，且丁烷含量波动较为剧烈，这是因为计量站B、C中正庚烷含量发生了明显波动。除此之外，其余组分的计量误差均在1%以下。

从上述结果可知，可以通过混合前管道气质的波动程度判断混合后天然气气质会发生变化，但这种变化无明显规律。这是因为天然气混合是一个十分复杂的过程，与流量、压力、温度及管道夹角等参数有关。

在气质波动较大时，混合后气体计量误差与模拟误差偏大，这是因为气质波动大，管道内气体流动不稳定，计量设备的计量结果存在误差。虽然各组分的计量值与模拟值存在误差，但是只要最终计算得到的发热量误差在标准规定的范围内，该模型的精确度便可以得到验证。

根据模型计算得到的状态参数和气质组成，计算得到标准状况下不同时刻的发热量数据，分别将高位体积发热量和低位体积发热量数据绘图，结果如图12所示。

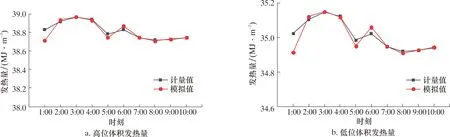
图12 发热量计量和模拟误差Fig.12 Errors between measured and simulated calorific values

从图12可以看出，发热量最大偏差出现在1：00，其最大偏差分别为0.305%和0.313%，均小于GB/T 18603—2014 中规定的0.5%，满足A级计量场站精度要求。发热量在2：00、3：00、6：00时升高，在4：00、5：00时降低，这与气质的变化是同步的。

3 结论及认识

(1)提出了一种基于GERG-2008 方程的天然气发热量赋值计算方法。使用压力适用范围广、计算性能好的 GERG-2008 方程作为状态方程，采用无量纲亥姆霍兹自由能及其导数表达热力学参数，耦合组分输运方程，对天然气进行流动模拟和发热量赋值计算，结果表明，使用该方法计算得到的天然气温度、流量及压力的最大误差(差值)分别为0.22 ℃、0.17%、0.33%。

(2)提出了基于分流管道下游计量数据的自适应流量分配方法。通过构建Kriging代理方程简化计算过程，以温度、压力误差最小为优化目标，使用 NSGA-Ⅱ 遗传算法计算下游管道初始参数，基于计算结果更新Kriging代理模型，并对整根管道进行自适应模拟计算。经验证，流量分配计算中温度的最大差值为0.26℃，压力的最大误差为0.19%。

(3)采用交错网格处理管道结点结构，动量方程在动量控制体进行离散，其余方程在质量控制体内离散，进而进行气体混合计算，从而提升气质跟踪计算的精确性。经验证，天然气组分混合计算中，甲烷的最大误差为0.178%，乙烷的最大误差为0.698%，丙烷的最大误差为0.732%，其余组分误差均在1%以下；高位和低位体积发热量最大偏差分别为0.305%、0.313%，计算结果均满足GB/T 18603—2014中A级计量站的计量要求。

(4)本文的方法可以为能量计量的实施提供帮助，节约设备投资和计量站现场改造、施工费用。