基于混沌系统和RSA算法的图像加密算法
孙晓鹏,姚凤麒
(安徽工业大学 电气工程学院,安徽 马鞍山 243032)
0 引 言
数字图像作为一种多媒体资源,是新时代人们交流的重要手段,不仅可以承载大量信息,还可以直观形象地表达信息内容,在商业、教育、医学研究、航空航天、军事和政治等各个领域中得到了广泛的应用。一些图像可能涉及到国家安全和个人隐私,例如军事基地、卫星侦察和生物识别信息,而未经允许的密码分析对图像信息的安全传播构成了巨大的威胁。混沌系统因其天然的复杂性、随机性和跨学科性,为图像安全通信提供了良好的加密基础。因此,如何有效地利用混沌系统保护图像通信的安全问题引起了各国学者的高度关注[1-5]。
混沌理论是非线性科学中的重要研究方向,构造具有复杂性质的简单混沌系统仍然是理论研究的主要内容之一。摆玉龙等人提出了一种多涡卷混沌系统[6],并在物理层面实现其特性。臧鸿雁等人提出一种二次多项式混沌系统[7],借此构造了S盒算法。Li等人构造了一种5维多翼的混沌系统[8],具有高维数高复杂性的特点。Xiong等人首次提出了一种可以在不同参数下生成单卷、双卷、三卷和四卷吸引子的三维自治系统[9]。李茹依等人结合了混沌系统和生物神经系统,提出了一种高度非线性的混沌神经网络动力系统[10]。在混沌学的研究发展过程中,学者们发现并提出了大量的混沌系统,混沌系统的特性、作用与功能也被进一步发掘。
在早期的图像加密研究中,人们发现图像因其庞大的数据量和较强的冗余特性,一般的文本数据加密方法并不适合图像加密。而混沌系统对初值和系统参数的高度敏感性、优良的遍历性和伪随机性,使得它成为图像加密中的研究热点。因此,一些学者提出了基于混沌系统的DNA编码[11-12]、置乱扩散[13]、Arnold变换[14]、压缩感知[15]等技术的图像加密算法。然而上述算法中密码仅由唯一密钥决定,易受已知或选择明文攻击,且混沌系统维度较低,结构复杂。该文利用RSA算法的非对称密钥加密方法以及构造了一种具有较大李雅普诺夫指数的四维四翼混沌系统,弥补了这一缺陷,并基于构造的混沌系统提出了一种明文相关的图像加密系统,使得加密明文图像的密码与RSA算法中的公钥和密钥以及明文图像相关联。此加密系统利用明文相关的置乱和扩散将图像分成块,对每个块依次加密,每个块的密码流由其前一个块的密码块和密钥共同生成,即加密系统与明文相关,在一定程度上提高了抵抗选择或已知明文攻击,增强了系统安全性,提升了加解密速度。
RSA算法是一种非对称加密算法,由公钥、密钥、明文、密文四部分组成。RSA算法的安全性取决于对极大整数因数分解的难度,对一极大整数做因数分解愈困难,RSA算法愈可靠。因此,科研学者在图像加密领域对RSA算法进行了广泛的研究和应用[16]。Wang等人为了增强密码系统的安全性能,提出了一种结合RSA算法的混沌同步系统[17],实现了双重加密。Yosefnezhad提出了一种基于置乱算法和RSA算法的数字图像水印模型[18],通过对原图像进行离散小波变换和奇异值分解将水印嵌入到图像中,足以保证隐藏数据的安全性。该文基于RSA算法数据量大、鲁棒性强、计算效率高等特点生成混沌系统初始值,加强混沌系统随机性从而提高加密算法的安全性能。
1 新型四维四翼混沌系统
在一个三维自治混沌系统中加入了一个非线性状态反馈控制器w,从而得到了一个新型四维四翼混沌系统,其数学表达式为:
(1)
当系统参数a=10,b=2,c=12,d=50,e=5,由四阶龙格库塔计算得到四个Lyapunov指数,分别为LE1=2.80,LE2=0.04,LE3=-5.30,LE4=-50.54,系统存在一个正的Lyapunov指数且其数值较大。其相空间映射图如图1所示。
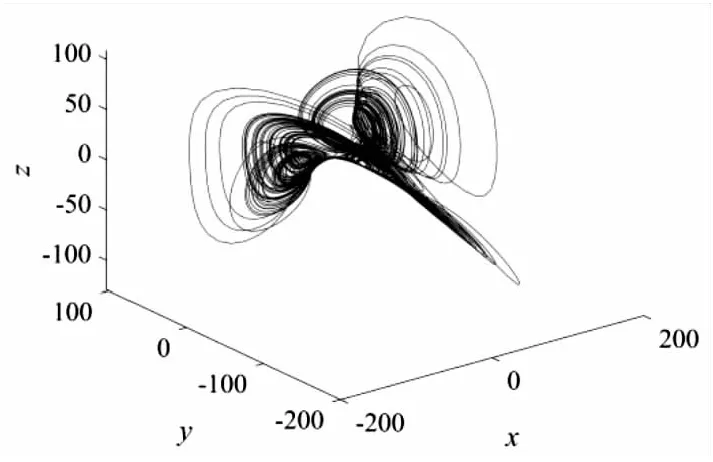
图1 混沌系统相图
2 动力学特性分析
2.1 平衡点和稳定性
(2)
当a=10,b=2,c=12,d=50,e=5时,求解公式(2),解得混沌系统有5个平衡点,S0=[0,0,0,0],S1,3=[±24.494 9,14.494 9,±7.101 0,±71.010 2],S2,4=[±24.494 9,-34.494 9,±16.899 0,±168.989 8]。在平衡点处对公式(1)线性化处理得其Jacobi矩阵:
(3)
令det=(J-λI)=0,其中I为单位矩阵,根据每个平衡点相对应的Jacobi矩阵可求得相应的特征值。根据特征值可知平衡点S0是不稳定的鞍点,其他四个平衡点S1、S2、S3、S4是不稳定的鞍焦点。
2.2 Poincaré映射
观察混沌系统在不同截面上的Poincaré映射也是一种分析混沌运动的有效方式。图2为x-y平面上的Poincaré映射,可以观察到系统运动轨迹在平面上留下的点是成片的密集点,证明系统运动是混沌运动。

图2 Poincaré截面图
2.3 Lyapunov指数谱和分岔图
令c∈(0,45),改变参数c的值,其他参数固定不变,通过Lyapunov指数谱和分岔图观察系统的运动状态。关于变量c变化的Lyapunov指数谱和分岔图分别如图3、图4所示。观察图中曲线可知,当c在区间(0,3.5],[4.2,6.3),[10.4,24.5),[24.7,38.1)内,系统存在正的Lyapunov指数并且出现周期分叉现象,此时处于混沌状态。当c在区间(3.5,4.2),(6.3,10.4),[24.5,24.7),[38.1,45]内,只存在一个Lyapunov指数等于零,其他三个指数均小于零,此时系统处于周期态,分岔图的变化趋势和Lyapunov指数谱几乎一致。

图3 Lyapunov指数谱

图4 随参数c变化的分岔图
3 电路仿真
本节采用Multisim软件平台设计混沌系统的电路,通过分析实验结果来进一步验证混沌系统的动力学特性。由理论数据分析可知,系统所有状态变量都超出了器件动态范围,为了避免输入信号过小造成乘法器输出误差过大,需要对系统变量进行适当的比例压缩变换。令x=kx,y=ky,z=kz,w=kw,t=τ0t。其中,k是比例变换因子且k=0.025,τ0是时间尺度变换因子,τ0=100。应用上述变换得到:
(4)
根据电路理论知识,可以得到该电路状态方程为:
(5)
根据状态空间方程可得到元件参数分别为C1=C2=C3=C4=0.1 μF,R1=10 kΩ,R2=R4=R9=R11=250 Ω,R3=50 kΩ,R5=8.3 kΩ,R6=R7=R12=R13=10 kΩ,R8=2 kΩ,R10=20 kΩ。
令uc1=x,uc2=y,uc3=z,uc4=w,则公式(4)和公式(5)是等价的。电路仿真结果如图5所示。通过比较可以发现电路仿真结果和数值分析结果基本一致,证实了该混沌系统存在吸引子,说明了该系统在物理上是可以实现的。

(a)x-y平面 (b)x-z平面图5 电路仿真
4 图像加解密方案
4.1 RSA算法
RSA算法是一种非对称加密算法,是三位数学家Rivest、Shamir、Adleman在1978年首次提出。与对称加密算法不同的是,RSA算法有两个不同的密钥,一个是公钥,一个是私钥。如果数据用公钥加密,则需要对应的私钥才能解密,相反如果用私钥加密,需要公钥解密。由于加密和解密使用两个不同的密钥,所以这种算法称为非对称加密算法。目前,RSA算法仍然是应用最广泛的非对称加密算法,其基于欧拉定理,安全性取决于大数模幂运算,位数越高则安全性越高。该文运用RSA加密算法生成混沌系统的初始值,这种算法可以使用接受方的已知公钥对密文进行加密,接收者收到密文后使用自己的私钥解密得到明文,在此过程中只有接收方可以获取到私钥信息。
加密步骤如下:
步骤1:随机选取两个不相等的质数p和q,计算出n=p*q和n的欧拉函数φ(n),其中φ(n)=(p-1)*(q-1)。
步骤2:随机选取一个整数e,满足1 步骤4:式(6)通过对加密后的密文和原文进行计算得到混沌系统的初始值。 (6) 将参数x0、y0、z0、w0代入混沌系统迭代生成混沌序列,为保证随机性,舍弃前100次迭代。设明文图像是大小为M×N的矩阵,令混沌系统迭代M×N次生成四个向量{xi,yi,zi.wi},i=1,2,…,M×N,由这4个向量生成4个大小为M×N的伪随机序列X1,X2和Y1,Y2,一个伪随机矩阵Z: (7) 在加取模扩散中,仅进行一次运算无法将明文的像素点信息完全扩散,所以利用伪随机序列X1和X2对原始图像矩阵P进行一次正向算法和一次逆向算法得到矩阵C: (8) 利用伪随机矩阵Z进行置乱处理以消除明文图像中相近像素点间的相关性,此过程中需要将得到的图像矩阵C中的像素点C(i,j)和C(m,n)对换位置,对换步骤如下: 步骤1:将C(i,j)与C(m,n)对换位置,其中C(M,1 toN)和C(1 toM,N)不参与位置置乱,位置(m,n)的计算方式如下: (9) 步骤2:此时得到的图像矩阵记为D,分别将D(M,j)和D(i,N)与D(m,n)对换位置: (10) (11) 步骤3:对换后的矩阵记为矩阵E,置乱E(M,N)的位置,对换规则如下: i=1,2,…,M-1,j=1,2,…,N-1 (12) 按照上述方法,先置乱矩阵C的元素C(1 toM-1,1 toN-1),接着分别置乱矩阵C的第M行C(M,1 toN-1)和第N列C(1 toM-1,N),最后置乱矩阵C的元素(M,N)得到置乱后的图像矩阵F。 将二维图像矩阵F转化为一维向量,借助于GF(17)有限域的乘法运算对矩阵F进行扩散处理: (13) 扩散得到的矩阵G即为加密后的最终图像,解密过程即上述加密过程的逆过程。 在USC-SIPI数据集中挑选了一些实验图像,观察算法的加密效果。在实验过程中,选取极大素数p=3 259,q=3 821和公钥e=1 288 367计算出私钥d=3 385 223。随机选取的4个极大整数为m1=178 334,m2=38 628,m3=92 873 897,m4=829 809,经过加密后得到密文c1=11 587 151,c2=1 799 483,c3=12 452 638,c4=4 198 591。由公式(6)得到混沌系统初始值x0=4.034 9,y0=3.797 9,z0=4.298 0,w0=3.928 2。实验图像的加密效果如图6所示,可以看到密文图像中呈噪声状分布,无法解读出有效信息,证明提出的加密算法是有效的。 (a)明文图像 (b)密文图像图6 加密效果 图像的直方图是重要的密文统计特性,直方图是表示数字图像中每个灰度出现概率的统计关系。理想的直方图分布应该均匀分布以抵御统计分析的攻击。以Lena图像为例,对图像直方图分布进行分析,并使用卡方检验来评估图像直方图的均匀性,卡方计算公式为: (14) 其中,i是灰度等级,fi是观察到的直方图中每个灰度值的像素点频数分布,g是理论频数分布,借助公式对图像进行卡方检验。 (a)明文图像 (b)密文图像图7 图像直方图 相关系数是图像相邻像素之间的线性相关性。在明文图像中水平、垂直和对角方向相关性较强,而在密文图像中这些方向上的相邻像素几乎没有相关性。相关系数公式如下: (15) 其中,rxy是相关系数,x和y是两个相邻像素的灰度值,取n对相邻像素点。该文从原始图像中随机取2 000对相邻像素点进行实验,对密文图像在水平、垂直、对角方向上的相关性进行分析,一般而言,相关系数的值介于-1和1之间,越接近于0加密效果越好。实验对Lena图像在水平、垂直、对角方向上的相关系数进行分析,并对比了不同的加密算法关于Lena图像的相关系数,分析数据列于表1中。 表1 相邻像素在不同方向上的相关系数 实验结果表明,提出的算法得到的密文图像相邻像素点在不同方向上的相关性接近于0,打破了明文图像中像素的相关性,近似无相关性,能够有效抵抗统计攻击。 信息熵反映了加密算法的安全强度和图像像素信息的不确定性,信息熵值越大,则不确定性越大,可视信息越少。信息熵的计算公式为: (16) 其中,L表示图像的灰度等级,p(i)表示灰度值i出现的概率。对于灰度等级为256的图像,其信息熵H的理论值为8。密文图像的信息熵越高,像素值的分布越均匀。表2给出了明文图像和相应密文图像的信息熵,彩色图像的信息熵为R、G、B三个通道信息熵的平均值。实验结果显示,密文图像的信息熵值非常接近于理论值8,而明文图像的信息熵与理论值有所差别,表明该算法可以有效防止信息泄露。 表2 不同图像的信息熵 一般来说,通过对比两张图像中明文图像和改变明文图像中一个像素的新密码图像来分析差分攻击中明文图像和密文图像的关系。利用NPCR和UACI来分析所提出的密码系统对于差分攻击的抵抗能力是一种有效且普遍的方式。NPCR是像素变化率,它表示原始图像中一个像素点变化时密文图像中变化的像素点数。UACI是统一平均变化强度,它表示原始图像中一个像素点发生变化时密文图像中像素点的差异程度。它们的计算公式如下: (17) 其中,图像大小为M×N,T为图像灰度等级,C1为密文图像,C2为原始图像中改变一个像素点后的密文图像。每一组实验中,仅随机改变原始图像中的一个像素点,变化量的值为1。从200组的实验结果中计算出NPCR和UACI的平均值。计算得出的平均值列于表3中。从表3中可以看到,NPCR均值和UACI均值分别接近于99.609 4%和33.463 5%,说明提出的加密系统在加密的过程中可以有效地将图像的微小差异传播到整个密文中,具有非常好的抗差分攻击能力。 表3 不同加密图像的NPCR和UACI均值 该文提出了一种新的四维四翼混沌系统,对其平衡点性质、稳定性、Poincaré截面图、Lyapunov指数谱以及分岔图做出分析,充分研究了系统的混沌特性。结合RSA算法和新混沌系统设计的图像加密系统将彩色图像分为R、G、B三个通道分别进行加密,并在第一阶段使用RSA算法生成安全密钥作为初始值。对密码系统进行性能分析,实验数据表明新混沌系统和RSA算法的引入使得密码系统对明文高度敏感,很大程度上增强了抗攻击性能和安全性,具有广泛应用于保密通信领域的潜在价值。亦可通过使用更加复杂的混沌系统或忆阻器等产生真随机序列进一步扩展研究工作。
4.2 混沌序列
4.3 加取模扩散
4.4 明文相关置乱
4.5 GF(17)域乘法扩散
5 安全性分析
5.1 加密效果

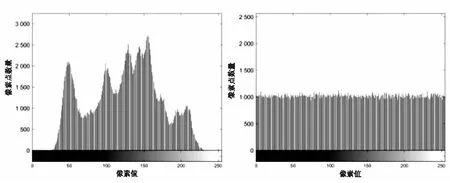
5.2 图像直方图分析

5.3 相关性分析

5.4 信息熵

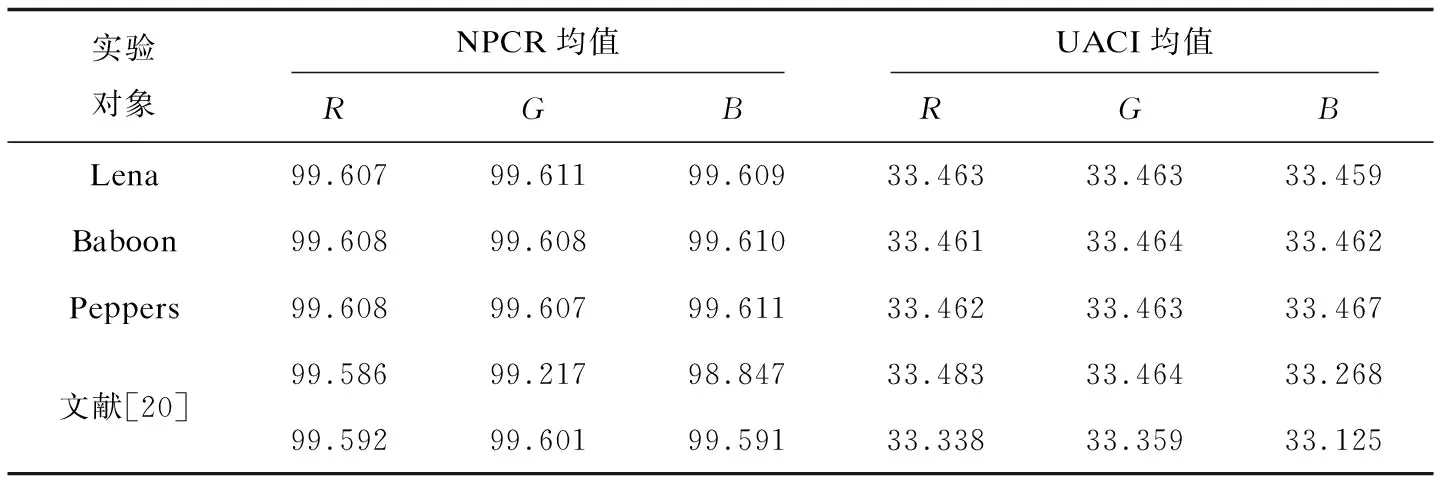
5.5 抗差分攻击性能分析
6 结束语

