基于EEMD-VMD-SSA-KELM模型的汛期日径流预测

吴小涛，袁晓辉，袁艳斌，毛雅茜，肖加清

（1. 黄冈师范学院数学与统计学院，湖北 黄冈 438000； 2. 华中科技大学土木与水利工程学院，湖北 武汉 430074； 3. 华中科技大学数字流域科学与技术湖北省重点实验室，湖北 武汉 430074； 4. 武汉理工大学资源与环境工程学院，湖北 武汉 430070）

0 引 言

径流预测可以为水资源的开发和管理、防洪、水旱灾害防治及社会可持续发展等提供决策支撑［1］。由于径流受到下垫面、水文气象和气候等因素的影响，呈现出非线性、非平稳等复杂特性，传统的物理机制水文模型的预测精度往往不高。基于数据驱动的机器学习模型如神经网络模型［2，3］、最近邻法［4］、支持向量机（Support Vector Machine，SVM）模型［5］等在充分挖掘历史径流数据内在规律的基础上，忽略复杂的下垫面情况、气象和气候等因素，建立未来径流与历史径流的映射关系，具有操作简单、预测精度高等优势，是目前主要的研究方向。苏辉东［6］等对同一组数据分别建立了分布式水文模型、BP神经网络模型和SVM 模型，通过模拟实验发现，SVM 模型的预测精度最高。然而SVM 模型的预测精度依赖于核函数中的参数以及惩罚参数的选取，并且其计算复杂度随样本规模的增加而变大。Huang［7］提出了核极限学习机（Kernel Extreme Learning Machine，KELM）这种单隐层前馈神经网络，该方法具有结构简单、运算速度快及泛化能力强等优点。Liu等［8］证明了当样本规模较大时，KELM 模型与SVM 模型的预测精度相差不大，但是KELM 模型的计算复杂度远远小于SVM模型。但是KELM 模型的预测精度依赖于核参数以及惩罚系数的选取，涂异等［9］提出用粒子群优化（Particle Swarm Optimization，PSO）算法来优化这两个参数，但是PSO 的寻优速度和优化精度不高。麻雀搜索算法（Sparrow Search Algorithm，SSA）是薛建凯等［10］在2020年提出的一种新的智能优化算法，与传统的PSO、蚁群算法等相比，SSA具有简单易实现，搜索精度高，收敛速度快，稳定性好，鲁棒性强等优点［11］。本文采用SSA 优化KELM 模型的核参数和惩罚系数。

利用数据分解算法如集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）算法、变分模态分解（Variational Modal Decomposition，VMD）算法等先对径流序列分解，可以有效提取隐含在径流序列中的有用信息，降低径流序列的非平稳性。吕晗芳［5］、孙望良［12］等建立了基于VMD算法的径流组合预测模型，李新华［13］等建立了基于小波包分解算法的径流组合预测模型，实验结果表明，组合了数据分解算法的模型较单一模型的预测精度高。文献［14］设计了基于EEMD 算法和VMD算法各自特点的二阶数据分解算法，称为EEMD-VMD 算法。EEMD-VMD 算法先利用EEMD 算法分解径流序列，再利用VMD算法进一步分解频率最大的分量，降低该分量及径流序列的不稳定性。EEMD-VMD 算法较EEMD 算法、VMD 算法具有更优的分解性能。

为了提高径流预测精度，本文综合考虑EEMD、VMD 处理非平稳径流序列的性能以及KELM 运算速度快、泛化能力强等优点，设计了一种基于EEMD算法、VMD算法和SSA优化KELM的组合径流预测模型，简称EEMD-VMD-SSA-KELM 模型。即首先对原始径流序列利用EEMD-VMD 算法分解；接着，对分解得到的每个分量分别建立SSA 优化的KELM 模型进行预测；最后，重构分量的预测结果得到原始径流序列的预测结果。本文将该模型应用于湖北宜昌寸滩水文站的汛期日径流预测，并与传统的BP 神经网络模型、最小二乘支持向量机（Least Squares Support Vector Machine，LSSVM）模型等进行比较，采用误差指标进行评价分析，验证该模型的适用性。

1 研究方法及模型建立

1.1 EEMD-VMD算法

EEMD算法依据序列的极值能有效分解出反映序列总体变化情况的趋势分量、反映序列周期性等特征的细节分量和反映噪声、干扰特征的随机分量。趋势分量和细节分量的波动频率较随机分量小很多，采用预测模型对其预测时，预测精度往往较高。但是随机分量由于其波动频率最大且规律性差，采用预测模型对其预测时，预测精度非常低，影响了序列的整体预测精度。由于VMD 算法依据序列的中心频率能将序列分解为多个不同频率的分量，故本文利用VMD算法对波动频率最大的随机分量再次分解，得到若干个频率不同、较随机分量更稳定的分量。EEMD-VMD 算法能有效降低序列的不稳定性，减小随机分量对序列的整体预测精度造成的影响［14］。利用EEMD 算法分解序列得到的分量个数由序列的长度确定，而利用VMD算法分解序列得到的分量个数K须要先确定，本文采用文献［15］中的最优变分模态分解算法来确定K的值。

1.2 SSA优化KELM 模型

SSA 是一种模拟麻雀种群在觅食、反捕食过程中的搜索行为的智能优化算法。种群中适应值较高的麻雀被称为发现者，负责搜索食物并提供食物所在的区域或方向；其余的麻雀被称为加入者，通过发现者提供的信息觅食。适应值最差的麻雀由于得不到食物会飞出食物所在区域，另寻他处觅食。麻雀之间会互相竞争，因而其身份也会动态变化，但是麻雀总数和比例保持不变。另外，种群中的麻雀一旦发现捕食者会立刻发出警告信息，所有麻雀飞出觅食区域，发现捕食者的麻雀被称为侦查者。SSA 模拟发现者的行为实现全局搜索，模拟加入者的行为实现局部探索，模拟适应值最差的麻雀以及麻雀的反捕食行为扩大搜索区域。发现者的位置更新策略［10］如式（1）所示。

式中：t为当前迭代数；Xt+1i为第i只麻雀在第t+1次迭代时的适应值，α∈(0，1)为随机数；itermax为最大迭代次数；R2和ST分别表示预警值和安全值；Q为服从标准正态分布的随机数；L为全一行向量。加入者的位置更新策略［10］如式（2）所示。

式中：Xtw为麻雀的最差位置；Xtp为发现者的最佳位置；A+为元素随机取-1 或1 的行向量。侦查者的位置更新策略［10］如式（3）所示。

式中：Xtb为全局最佳位置；γ为步长控制参数；K∈(0，1)为随机数；ε为保证分母不等于0 的常数；fi为当前麻雀的适应值；fb、fw分别为当前全局最优适应值和最差适应值。

KELM 是一种改进的ELM 模型。对于含有n个样本的数据集{(x1，t1)，(x2，t2)，…，(xn，tn)}，其中xi=[xi1，xi2，…，xid]∈Rd是输入数据，i= 1，2，…，n，ti=[ti1，ti2，…，xik]∈Rk是输出数据。ELM 模型假设隐含层有m个节点，其输出函数为h(x) =[h1(x)，h2(x)，…，hm(x)]=H，隐含层与输出层节点之间的连接权重为β=[β1，β2，…，βm]，则其输出可表示为：

为了最小化训练误差ε和连接权重β，ELM 模型利用结构风险最小原理，构造二次规划问题如下：

式中：C为惩罚系数；εi为第i个误差变量，ε=[ε1，ε2，…，εn]。

进一步通过拉格朗日乘子αi，将式（5）转化为如下无约束优化问题：

其中，I是单位矩阵，y=[y1，y2，…，yn] 是期望输出向量。

ELM中的h(x)为随机映射，影响了ELM模型的稳定性和预测精度，Huang提出采用核函数代替h(x)，将训练样本映射到高维空间，建立了基于核的ELM 模型即KELM 模型［7］。KELM 模型的核矩阵定义为Ω=HHT，其元素定义为Ω(i，j) =h(xi)h(xj)=K(xi，xj)，其中K(xi，xj) 是核函数。KELM 模型的输出可表示为：

其中，核函数K(xi，xj)选择高斯核函数，定义如下：

其中，σ为核参数，其取值直接影响到KELM 的泛化能力。另外，惩罚系数C会影响KELM 模型的预测精度，C的值偏小会产生较大的训练误差，偏大会产生过拟合。为了提高KELM 模型的泛化能力和预测精度，本文采用SSA 来优化σ和C。选择平均绝对百分比误差作为SSA的适应值计算函数，即：

式中：Num为样本总数；t*和y*分别为径流的实测值和预测值。

SSA优化σ和C的步骤为：

步骤1：初始化参数，包括最大迭代次数、种群规模，发现者数量、加入者数量和侦查者数量、预警值、麻雀的初始位置（即σ、C）及其优化区间等。

步骤2：根据初始参数由式（4） ～（8）及式（10）计算得到麻雀个体的初始适应值，保存适应值最优、最差的麻雀个体的位置Xb和Xw。

步骤3：由式（1）更新发现者位置，由式（2）更新加入者位置，由式（3）更新侦查者位置。

步骤4：计算更新位置后所有麻雀的适应值，更新Xb和Xw。

步骤5：判断是否满足迭代终止条件（最大迭代次数或误差）。如果不满足则返回到步骤3，满足则寻优结束，将适应值最优的麻雀的位置σ和C作为输出。

1.3 EEMD-VMD-SSA-KELM 预测模型

为了提高径流的预测精度，本文设计了基于“分解-建模预测-重构”思想的径流预测框架，如图1 所示，具体预测步骤如下：

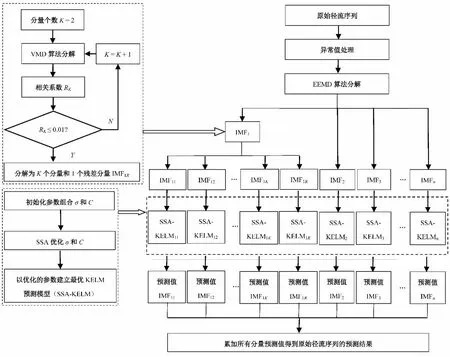
图1 EEMD-VMD-SSA-KELM 预测模型框架图Fig.1 Framework diagram of EEMD-VMD-SSA-KELM prediction model

步骤1：数据预处理。采用拉依达准则处理原始径流序列中的异常值。

步骤2：EEMD分解。利用EEMD算法对预处理后的径流序列进行分解，得到n个分量IMF1～ IMFn。

步骤3：VMD分解。利用VMD算法对频率最大的分量IMF1进行分解，得到K个分量IMF11～ IMF1K以及一个残差分量IMF1R。

步骤4：数据准备。将每个分量归一化后划分为训练数据集和测试数据集。

步骤5：建模预测。基于每个分量的训练数据集建立SSA优化的KELM模型，并对测试数据集进行预测，将预测结果作反归一化处理。

步骤6：重构。累加步骤5 中所有分量的预测结果，得到原始径流序列的预测结果。

2 实例分析

2.1 数据来源

选取湖北宜昌寸滩水文站2006-2012年间的汛期日径流序列进行实验。寸滩水文站是国家基本水文站、中央报汛站，其防汛测报地位和功能十分突出。因为2006-2012 年间每年的1-5月以及10-12月的日径流较小且波动不大，而6-9月处于汛期，其日径流大且波动也较大，所以本文仅对6-9月的径流进行预测。根据拉依达准则对2006-2012 年间每年的6-9 月的日径流数据进行处理后得到854 个数据，汛期日径流随时间的变化情况如图2所示。

图2 汛期日径流序列曲线图Fig.2 Daily runoff sequence curve in flood season

2.2 数据分解

对上述径流序列利用EEMD 算法进行分解，得到9 个分量IMF1～IMF9，如图3所示。

图3 EEMD 算法分解结果Fig.3 Decomposition results using EEMD algorithm

图3中，IMF9是趋势分量，波动频率最小，IMF2～IMF8是细节分量，IMF1是随机分量，波动频率最大。利用VMD 算法对IMF1进一步分解，当模态个数K=9 时，残差分量与IMF1的相关系数RK等于0.001，小于给定的阈值0.01，从而K的值取9。9 个分量和1 个残差分量分别记为IMF11～IMF19、IMF1R，分解结果如图4所示。

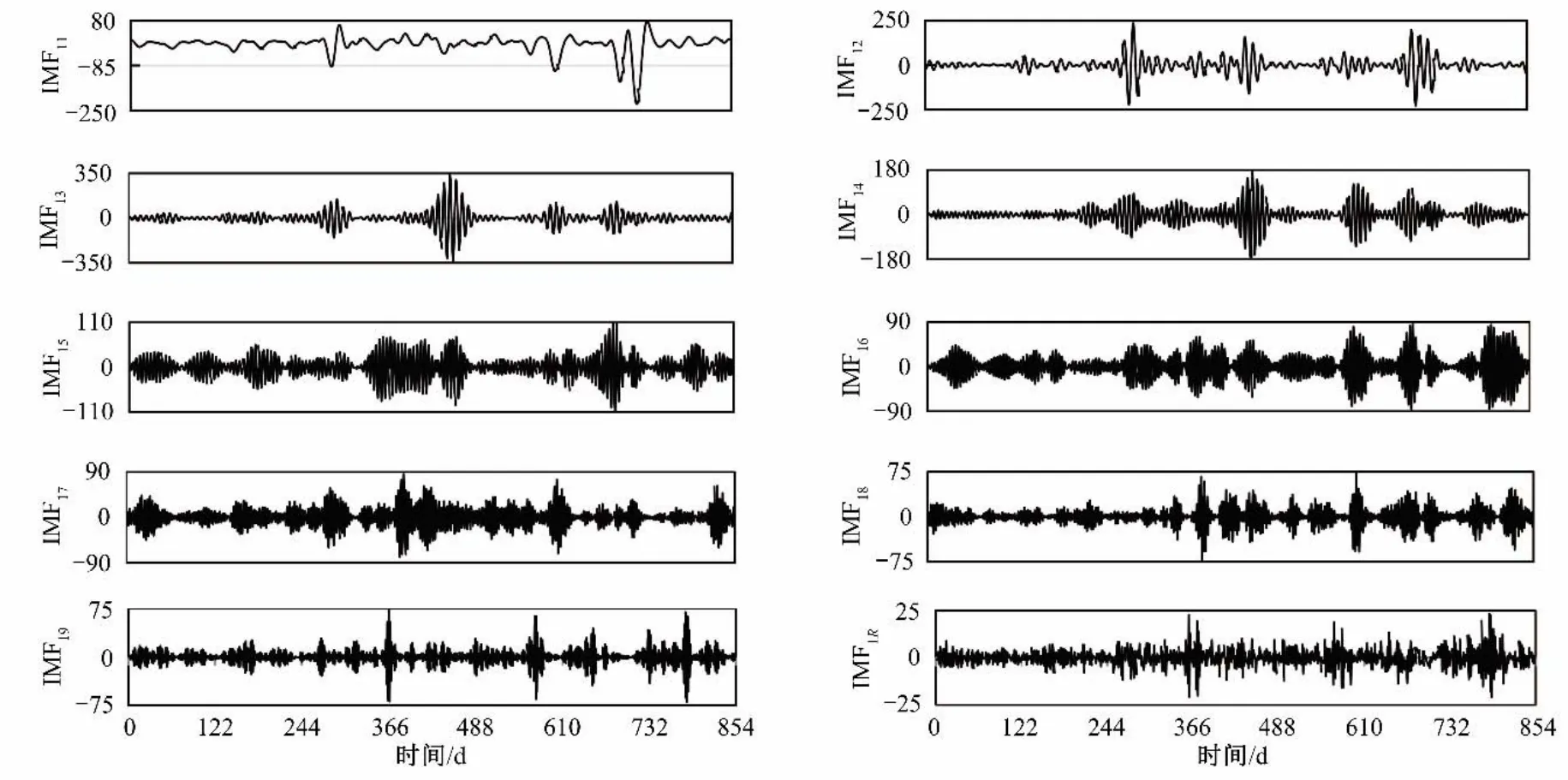
图4 VMD算法分解结果Fig.4 Decomposition results using VMD algorithm

从图4 可以看出，IMF11的波动频率最小，IMF12～IMF19的波动频率逐渐增加，但是这些分量的径流值几乎对称分布在零的上下两侧，稳定性较IMF1显著增强。尽管IMF1R的波动频率最大，但是其变化范围非常小，其预测结果对序列的整体预测精度影响很小。

2.3 预测模型的输入与输出

对2012 年6-9 月每日的径流进行预测，选择2006-2011 年间每年6-9月的日径流数据（共732个，编号为1～732）作为训练数据，2012 年6-9 月的日径流数据（共122 个，编号为733～854）作为测试数据。径流序列或各个分量的预测模型的输入维度根据径流序列或分量的偏自相关系数（PACF）的延迟时间数来确定［16］。例如，径流序列的PACF结果如图5 所示，从图5 可以看出，在所有这些延迟中，前3个延迟超过了95%置信区间对应的阈值，因此，对径流序列直接进行预测的预测模型的输入维度取3。

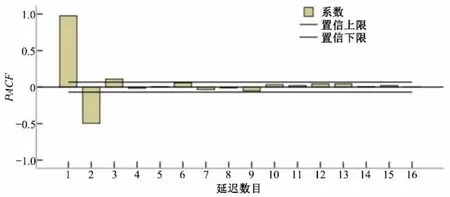
图5 径流序列的PACFFig.5 PACF of Runoff Series

各个分量的预测模型的输入维度如表1所示。

表1 各个分量的预测模型的输入维度Tab.1 Input dimension of prediction model of each component

2.4 预测结果分析

将本文提出的EEMD-VMD-SSA-KELM 模型与SSA-BP 模型、SSA-LSSVM 模型、SSA-KELM 模型、EEMD-SSA-KELM 模型和EEMD-VMD-PSO-KELM 模型作比较。前3 种模型中，采用SSA 分别优化BP 神经网络模型的神经元个数、LSSVM 模型的参数以及KELM 模型的参数。EEMD-SSA-KELM 模型和EEMD-VMD-PSO-KELM 模型与提出的模型类似，区别在于EEMD-SSA-KELM 模型只组合了EEMD 算法，提出的模型组合了EEMD-VMD 算法；EEMD-VMD-PSO-KELM 模型采用PSO优化KELM 模型的参数，提出的模型采用SSA 优化KELM 模型的参数。SSA-BP 模型、SSA-LSSVM 模型和SSA-KELM 模型的输入维度均为3，EEMD-SSA-KELM 模型、EEMD-VMD-PSOKELM 模型以及EEMD-VMD-SSA-KELM 模型中的分量的预测模型的输入维度如表1。6 种预测模型的预测曲线图如图6所示。

图6 预测曲线图Fig.6 Prediction curves

从图6 可以看出，除了矩形区域对应的时间段（编号为777～792）外，6 种模型在其余时间的预测曲线整体上与实测值曲线变化趋势类似。在所有时间点，EEMD-VMD-SSA-KELM模型和EEMD-VMD-PSO-KELM 模型的预测值与实测值无限接近，因此其预测精度最高，EEMD-SSA-KELM 模型的预测精度较高，SSA-BP 模型、SSA-LSSVM 模型和SSA-KELM 模型的预测精度最低。进一步，将矩形区域的预测曲线放大，如图6中的小图所示，可以看出，组合了数据分解算法的EEMD-SSAKELM 模型、EEMD-VMD-PSO-KELM 模型和EEMD-VMDSSA-KELM 模型的预测曲线较没有组合数据分解算法的SSABP 模型、SSA-LSSVM 模型和SSA-KELM 模型的预测曲线更接近于实测值曲线。统计6 种预测模型的误差指标MAPE、MRE、RMSE和R2如表2所示。

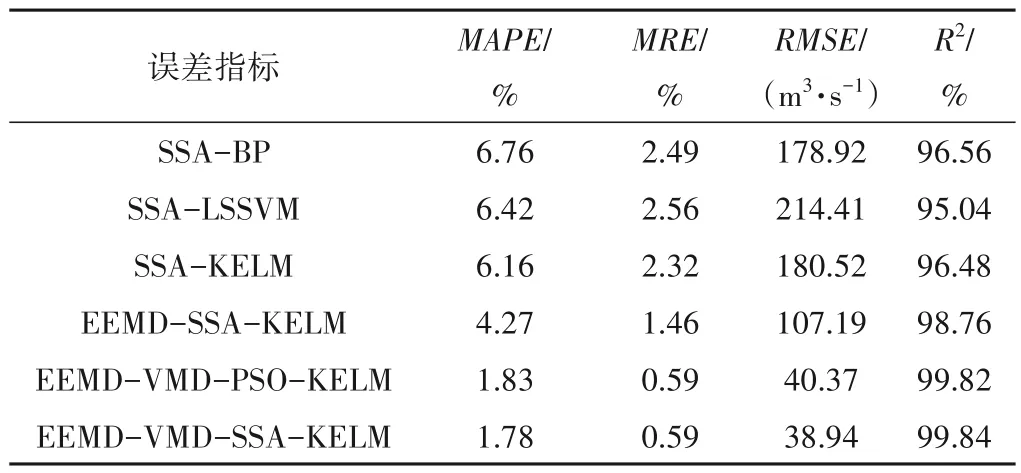
表2 预测误差表Tab.2 Error values

由表2 可知，SSA-LSSVM 模型的4 种误差指标值均劣于SSA-KELM 模型，说明KELM 模型的预测精度优于LSSVM 模型。没有组合数据分解算法的SSA-BP 模型、SSA-LSSVM 模型和SSA-KELM 模型的MAPE均高于6%，MRE均高于2%，RMSE均高于170 m3∕s，R2均低于97%，而组合了数据分解算法的3 种模型的MAPE均低于5%，MRE均低于1.5%，RMSE均低于110 m3∕s，R2均高于98%，说明组合了数据分解算法的预测模型的预测精度明显优于没有组合数据分解算法的预测模型。进一步对比EEMD-SSA-KELM 模型和EEMD-VMD-PSO-KELM 模型、EEMD-VMD-SSA-KELM 模型的误差指标值可以看出，EEMDSSA-KELM 模型的4 种误差指标值均劣于后两种模型，说明组合EEMD 算法的预测模型的预测精度劣于组合了EEMD-VMD算法的预测模型，即EEMD-VMD 算法较EEMD 算法具有更优的分解性能。对比EEMD-VMD-PSO-KELM 模型和EEMDVMD-SSA-KELM 模型的4 种误差指标值，除了MRE相同，均为0.59 % 之外，EEMD-VMD-SSA-KELM 模型的其余3 个误差均优于EEMD-VMD-PSO-KELM 模型，说明了SSA 较PSO 具有更优的寻优精度。6 种预测模型的4 种误差指标的直方图如图7所示。

图7 误差指标直方图Fig.7 Histogram of error index

由图7（a）可知，对于MAPE指标，SSA-BP 模型的MAPE最高，等于6.76%，而EEMD-VMD-SSA-KELM 模型最低，只有1.78%，说明提出的模型的预测值的平均绝对百分比误差最小。由图7（b）可知，对于MRE指标，SSA-BP 模型、SSA-LSSVM 模型和SSA-KELM 模型的MRE均超过了2%，而EEMD-VMD-SSAKELM 模型的MRE最低，仅为0.59%，说明提出的模型的预测值和实测值之间的接近程度最高。由图7（c）可知，对于RMSE指标，SSA-LSSVM 模型的RMSE最高，等于214.41 m3∕s，而EEMDVMD-SSA-KELM 模型的RMSE最低，仅为38.94 m3∕s，说明提出的模型的预测值与实测值之间的偏差最小。由图7（d）可知，对于R2指标，EEMD-VMD-SSA-KELM 模型的R2达到了99.84 %，高于其余5 种模型，说明提出的模型的拟合程度最高。综上所述，EEMD-VMD-SSA-KELM 模型的4个误差指标MAPE、MRE、RMSE和R2均最优，其预测精度远优于SSA-BP、SSA-LSSVM、SSA-KELM 和EEMD-SSA-KELM 等模型。EEMD-VMD-SSAKELM 模型能较准确的模拟复杂多频信息的汛期日径流变化趋势，模型及方法可为水文预测及相关预测研究提供参考。

3 结 论

针对汛期日径流序列非线性、非平稳等特点导致径流预测精度低的问题，本文提出了一种基于EEMD-VMD 算法和SSA优化KELM 的组合径流预测模型（EEMD-VMD-SSA-KELM），并将该模型应用于湖北宜昌寸滩水文站的汛期日径流预测，得到如下结论。

（1）在本实验中，KELM 模型的预测精度优于LSSVM 模型，SSA 的优化精度优于PSO，EEMD-VMD 算法的分解性能优于EEMD算法。

（2）组合了数据分解算法的EEMD-SSA-KELM 模型、EEMD-VMD-PSO-KELM 模型和EEMD-VMD-SSA-KELM 模型的预测精度明显优于没有组合数据分解算法的SSA-BP 模型、SSA-LSSVM 模型和SSA-KELM 模型。但由于组合了数据分解算法的预测模型要对每个分量建立模型预测，因此其时间复杂度更高。

（3）EEMD-VMD-SSA-KELM 模型的预测精度远优于SSABP、SSA-LSSVM、SSA-KELM、EEMD-SSA-KELM 等模型，能较准确的模拟复杂多频信息的汛期日径流的变化趋势。

本文的不足之处在于只对汛期日径流序列进行了单步预测，在后续研究中，可以用提出的模型在单步预测的基础上，进一步进行多步预测。另外，对于提出模型复杂度高的问题，可以考虑引入样本熵，将复杂性相近的分量重组，减少分量个数，降低模型的时间复杂度。