基于两阶段分解和可解释机器学习的中长期径流预测

薛联青，周天文，刘远洪，杨丽娟

（1. 河海大学水文水资源学院，江苏 南京 210098； 2. 皖江工学院水利工程学院，安徽 马鞍山 243031）

0 引 言

准确可靠的中长期径流预测对流域防洪抗旱、水资源规划与管理具有重要意义［1］，但径流在时间和空间尺度上表现出不确定性［2］，对未来的径流进行精准预测具有很大难度。近年来，基于数据驱动的机器学习模型因其强泛化性和较好的鲁棒性而广泛地被用于径流预测［3，4］。然而，由于径流序列的非线性和复杂性，在缺少对原始数据预处理的情况下机器学习模型难以识别这些特征，从而给准确的径流预测带来挑战［5］。通过选择合适的数据预处理方法如分解技术，可以滤除混合噪声和干扰，从而提高预测精度［6］。如梁浩等［5］基于EMD（Empirical Mode Decomposition）、EEMD（Ensemble Empirical Mode Decomposition）和WD（Wavelet Decomposition）分解方法构建多种混合模型，对渭河流域月径流进行预测，得出混合模型预测精度均高于单一模型的结论。

单一分解技术往往不能完全处理随机和不规则数据序列的非平稳性［7，8］，近年来，有学者在单一分解技术的基础上提出了两阶段分解，如Chen 等［9］构建了基于EEMD-VMD 两阶段分解的SVM 模型，对乐昌峡流域平石水文站年径流进行预测，提高了预测精度。但月径流较年径流系列表现出更强的非线性和季节性，EEMD 在模态混叠和分解效率上仍有不足［10，11］，而STL 能够正确揭示和呈现数据中的基本特征［12］，有更高的分解效率，适用于月径流序列。此外，以往的研究大多未对模型预测结果的成因进行解释［8］，而SHAP 是一种基于博弈论的全局灵敏度分析方法［13］，可用于分析模型各输入特征对预测结果的贡献，从而提高模型的可靠性和应用价值。

研究构建了基于两阶段分解（STL-VMD）的机器学习月径流预测模型，同时构建了基于未分解、单一分解（STL、VMD）预处理的对比模型，以期揭示STL-VMD 对不同机器学习模型的改善效果，最后基于SHAP 值对最优模型进行可解释性分析以提高模型的可信度。

1 研究方法

1.1 分解方法

1.1.1 基于Loess的季节趋势分解

STL 是以局部加权回归（Loess）作为平滑方法的时间序列分解方法，具有线性最小二乘回归的简单性和非线性回归方法的适应性等优点［14］。该方法将原始的时间序列分解为趋势项、季节项和残差项，使用稳健估计避免了在趋势项和季节项中由异常值引起的误差，且趋势项平滑程度和季节项变化速率都可通过相应的参数进行控制，较EEMD 的月径流序列分解效率更高。

1.1.2 变分模态分解

变分模态分解（VMD）是一种自适应、完全非递归的模态变分和信号处理方法［15］，在获取分解分量的过程中通过迭代搜寻变分模型最优解来确定每个分量的频率中心和带宽，从而能够自适应地实现信号的频域剖分及各分量的有效分离，具有较强的噪音鲁棒性和较弱的端点效应，解决了EMD 和EEMD 模态混叠的问题，有更大的潜力准确预测径流时间序列［11］。

1.2 机器学习模型

1.2.1 长短期记忆网络

长短期记忆网络（LSTM）是一种特殊的递归神经网络（Recurrent Neural Network， RNN）［16］，通过门结构设计选择性的遗忘或更新历史信息，解决了传统RNN的梯度消失和梯度爆炸问题。模型包含输入层、隐藏层和输出层，输入层需提供数据类型为［z，m，n］的三维张量X，其中z为批次大小（batch_size），即输入数据的序列长度；m为时间步长（time_step），即模型依次输入滑动窗口t-m至t-1时刻的特征序列值（图1红框所示），根据径流序列的周期性，本文m取值为12，即根据过去12 个月的特征序列值预测当月径流值；n为输入特征种类（feature）。

图1 LSTM模型输入数据处理过程Fig.1 LSTM model input data processing process

1.2.2 卷积神经网络

卷积神经网络（CNN）是一类包含卷积计算且具有深度结构的前馈神经网络［17］，由多层感知机（Multilayer Perceptron，MLP）演变而来。典型的卷积神经网络由卷积层、池化层和全连接层构成，分别实现对输入数据特征的自动提取、降维和输出。卷积层通过创建卷积核对输入进行卷积，以生成输出张量，输出维度通过参数filters 的大小确定，当卷积层为模型第一层时，需提供与LSTM 模型输入数据类型相同的三维张量X［z，m， n］，m取值及初始输入特征种类均与LSTM模型相同。

1.2.3 支持向量回归

支持向量回归（SVR）是基于统计学理论的机器学习方法［18］，遵循结构风险最小化原则，通过将低维样本数据映射到高维特征空间，并对支持向量进行回归拟合，实现预测。与LSTM 和CNN 模型不同，SVR 模型输入数据X类型为形如（n_samples， n_features）或（n_samples， n_samples）的数组或者稀疏矩阵，其中n_samples为样本数量，n_features为特征数量。

1.3 组合模型构建

基于月径流序列的数据特征及上述各模型的基本原理，本文根据“分解-预测-重构”的思想，构建了基于STL-VMD 的月径流预测集成模型，该模型主要包括两阶段分解、输入特征优选、机器学习模型预测和结果重构4 个阶段，构建流程概述如下：

（1）两阶段分解。

①STL 分解：首先采用STL 方法将原始的径流序列Q分解为趋势项QTRE、季节项QSEA和残差项QRES，即：

②VMD 分解：采用VMD 方法对随机性较强的残差项QRES进一步分解以剔除噪声，得到K个分解模态VMFi（i=1，2，…，K），即：

（2）输入特征优选。计算滞时为一个月的径流序列与前期径流、气象数据、气候指数等14种特征的皮尔逊相关系数，选择皮尔逊相关系数绝对值大于0.2的特征作为模型输入特征［9］。

（3）机器学习模型预测。将优选后的特征整理成图1 机器学习模型能够识别的格式，为进一步提高预测精度，通过粒子群优化算法（Particle Swarm Optimization， PSO）［19］对模型超参数进行寻优，寻优步骤如下：

①初始化PSO 参数，即粒子数、最大迭代数和惯性因子等，并设置待优化超参数搜索范围，对于LSTM和CNN模型，以定型周期和批次大小为优化对象，对于SVR 模型，以惩罚系数和核函数系数为优化对象；

②选用MAE为优化目标函数，求得各粒子对应的适应度值，得到初始的个体最优适应度值、全局最优适应度值及对应的参数；

③更新粒子的速度和位置；

④令k=k+1，重复步骤②～③，直到k为最大迭代数，输出最终求解结果。

（4）结果重构。将趋势项、季节项和K个分解模态的预测结果线性加和，得到月径流预测的最终结果。

1.4 评价指标

选取平均绝对误差（MAE）、平均绝对百分比误差（MAPE）和纳什效率系数（NSE）来综合评价模型预测精度。

MAE表示预测值和实测值之间绝对误差的平均值：

MAPE表示预测值和实测值之间相对偏离程度：

NSE反映了预测值和实测值的拟合程度：

式中：n为样本数；yi为第i个实测值；为实测值的平均值；xi为第i个预测值。

1.5 可解释机器学习方法

可解释性不足是机器学习模型使用的限制之一，SHAP 是一种基于博弈论的可解释机器学习方法，通过构建不同输入变量的组合比较模型输出的平均变化，进而量化各特征对模型结果的具体贡献，每个输入变量的SHAP 值是该变量边际贡献的加权平均值：

式中：ϕi表示输入变量i的SHAP 值，该值为正（负）时表明变量i对预测结果起提升（降低）作用；n代表输入变量个数；N代表输入变量的完整集合；S表示除去变量i的集合，是N的子集；F（S）表示基于输入S的预测结果。

2 实例应用

2.1 研究区概况

澧水位于湖南省西北部，属洞庭湖四大水系之一，于小渡口注入西洞庭湖，全长390 km，落差1 439 m，流域面积18 583 km2，地势西北高东南低，流域概况如图2 所示。石门站为澧水流域控制站，多年平均月径流量458.51 m3∕s，最大月径流量2 786.80 m3∕s。流域雨量丰沛，洪水发生频繁，大洪水集中在6-8月，下游与长江支流松滋河交汇的松澧地区，历年来是洞庭湖区洪涝灾害最为严重的地区之一，开展澧水流域径流预测的研究对流域防洪减灾具有重要意义。

图2 澧水流域概况图Fig.2 Overview of Lishui Basin

2.2 数据处理

水文过程与大时空尺度上的大气环流过程、气象条件和海洋条件等遥相关［20］，本文共搜集了径流、降雨、蒸发、北极涛动等14种特征作为模型初始输入特征，数据类型及相关信息如表1所示，并基于皮尔逊相关系数对初始输入特征进行筛选，系数绝对值大于0.2 表示两变量存在相关关系，计算滞时（模型预见期）一个月的径流序列与14 种特征的皮尔逊相关系数，结果见表1，最终Q、M1、M2、M3、M5、C1、C2、C3、C5、C7 十种特征作为机器学习模型输入特征。

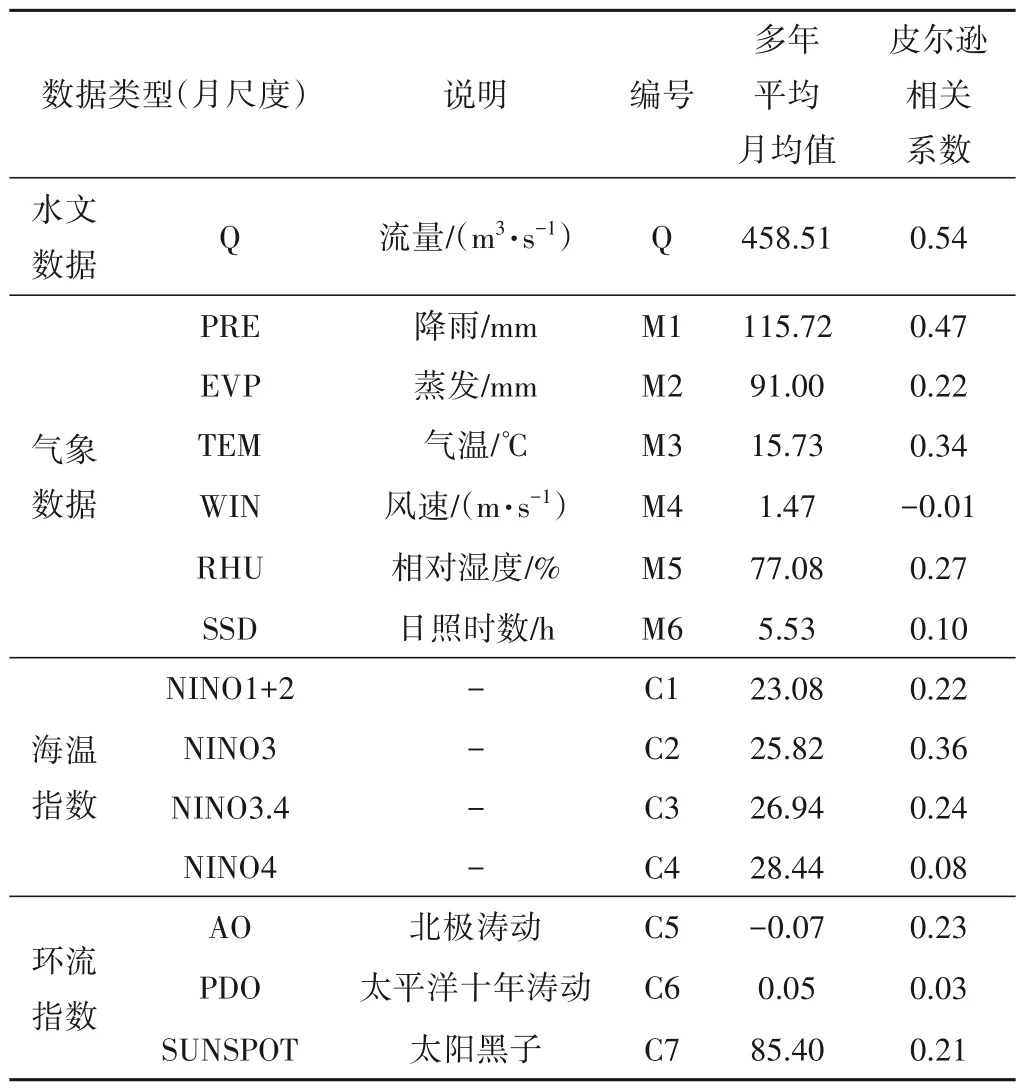
表1 澧水流域数据列表Tab.1 Data list of Lishui Basin

2.3 对照组建模流程

基于不同的分解方法构建了4组对比模型（Ⅰ～Ⅳ），建模流程如图3 所示。其中Ⅰ组为未分解预处理组；Ⅱ组为STL 预处理组；Ⅲ组为VMD 预处理组，根据文献［4］的模态个数确定方法，原始的径流序列被分解为IMF1～IMF8；Ⅳ组为STL-VMD 预处理组，径流残差项QRES被分解为VMF1～VMF8。对于Ⅱ～Ⅳ组，除根据皮尔逊相关系数选择的输入特征外，对各分解分量逐一预测时，该目标分量的前期序列被视为潜在输入特征。各特征按比例划分为训练期（70%，1960.01-2002.02）、验证期（15%，2002.03-2011.01）和测试期（15%，2011.02-2019.12）并进行归一化处理后输入到各机器学习模型中，训练期实现对模型的拟合，验证期判断模型是否过拟合或欠拟合，测试期用来评价模型泛化性［21］，通过PSO 对各机器学习模型超参数进行寻优，预见期为一个月，输出为径流值（Ⅰ组）或各分解分量的值（Ⅱ～Ⅳ组）。

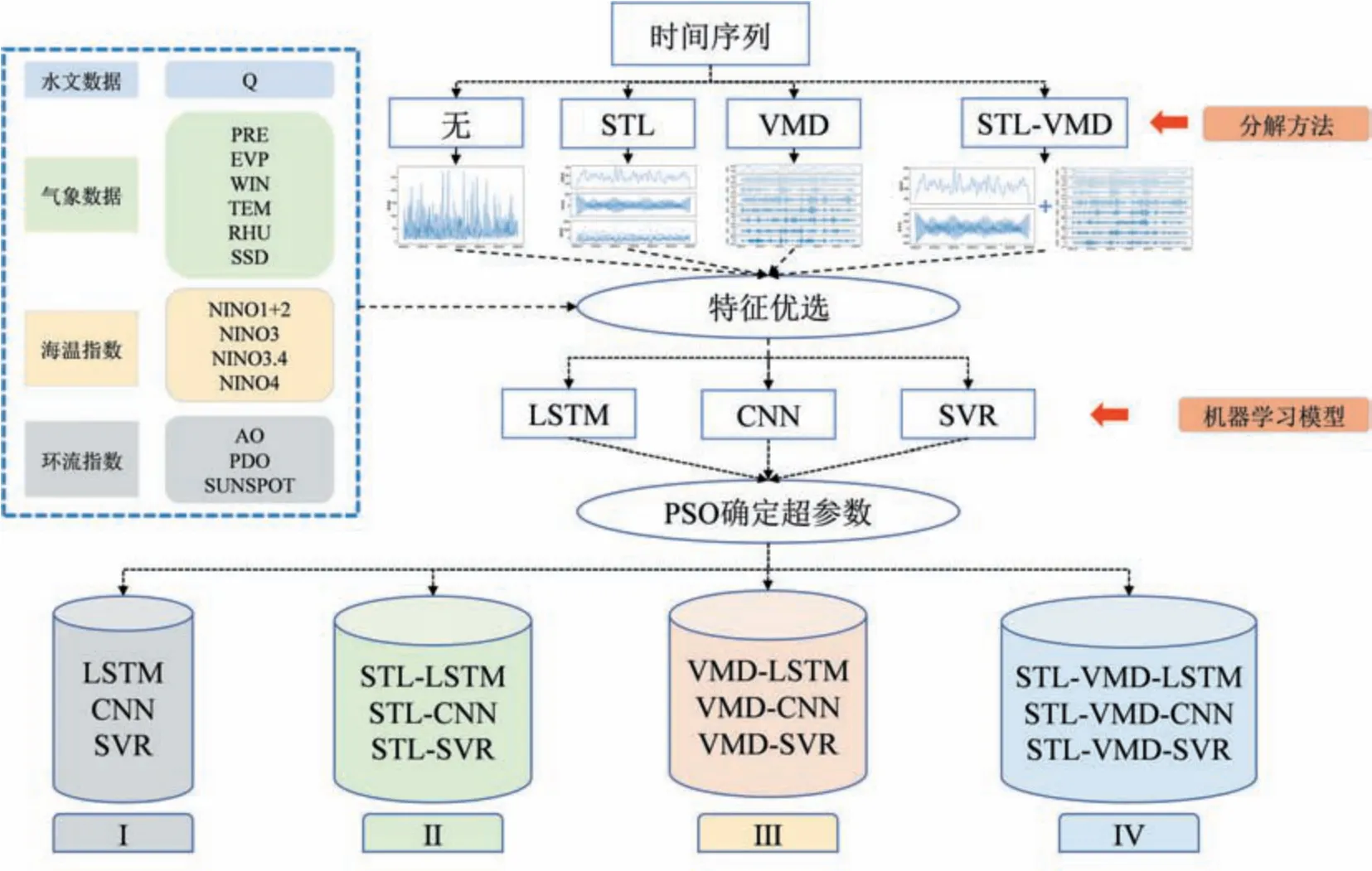
图3 对照组建模流程Fig.3 Modeling process of the control group

2.4 结果与分析

2.4.1 模型超参数寻优结果

本文粒子数和最大迭代次数分别设置为30 和200，惯性因子ω设为0.8，学习因子c1和c2设为2，对于LSTM 和CNN 模型，定型周期和批次大小搜索范围分别设为［100，500］和［16，256］，学习率通过观察测试期和验证期的loss 曲线手动调整进行寻优；对于SVR 模型，搜索范围统一设为［1×10-3，8］，核函数类型通过手动调整进行寻优；寻优结果见表2（Ⅰ组）。

表2 模型超参数（Ⅰ组）Tab.2 Model hyperparameters （group I）

2.4.2 径流预测结果

为定量评估各模型整体预测性能，表3 展示了各模型验证期和测试期预测值与实测值的MAE、MAPE 和NSE，从表3 可看出：测试期Ⅰ组MAE介于127.44～134.77 m3∕s，MAPE介于28.64%～34.34%，NSE介于0.63～0.64，Ⅱ组和Ⅲ组预测精度相似，MAE介于92.40～119.57 m3∕s，MAPE介于20.33%～27.97%，NSE介于0.71～0.82，Ⅳ组MAE介于55.65～111.57 m3∕s，MAPE介于9.61%～25.59%，NSE介于0.72～0.93，可见分解预处理可明显提升模型预测精度，且两阶段分解预处理效果整体优于单一分解；对于LSTM和CNN模型，组内指标变化幅度小于组间变化幅度，可见分解预处理造成模型输入的改变，进而对模型精度的提升优于模型结构变化的提升；Ⅰ～Ⅳ组中SVR 模型预测精度均不如LSTM 和CNN 模型，这可能由于径流序列过长，而SVR模型在短时间序列上表现更好有关［9］。

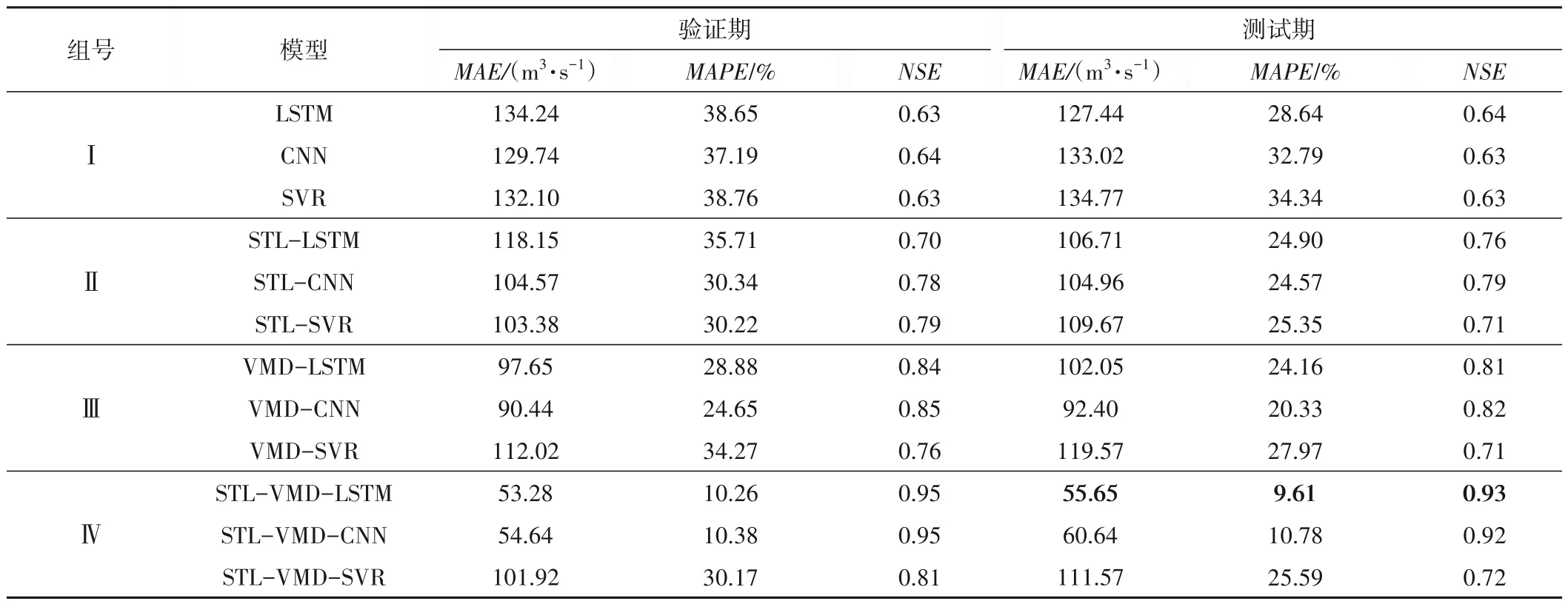
表3 各组模型径流预测精度评价Tab.3 Evaluation of model runoff prediction accuracy in each group

散点图可更直观的展示出预测值与实测值的拟合情况（如图4 所示），从图4（a）中可看出Ⅰ组各模型预测结果整体偏小，且这一现象在图4（a）～（d）中高流量事件的预测尤为明显；对比图4（a）和4（b）可看出STL 预处理对SVR 模型预测精度的提升较为显著，决定系数R2由0.57 提升至0.78；对比图4（a）和4（c）可看出VMD 预处理对CNN 模型预测精度提升较为显著，R2由0.65 提升至0.88；对比图4（a）和4（d）可看出STL-VMD 预处理对LSTM 和CNN 模型预测精度均有显著提升，R2由0.64 和0.65提升至0.94 和0.93，预测值更收敛于实测值。结合表3 数据可看出不同指标得到的模型性能优劣程度并不完全一致，如对于SVR 模型，根据MAE、MAPE和R2计算结果，最优模型为STLSVR 模型，而根据NSE计算结果，最优模型为STL-VMD-SVR模型，这与不同指标的评价角度不同有关。MAE和MAPE分别反映了预测值可能的误差范围、偏离程度，R2侧重于评估预测值与观测值的相关性，当模型预测结果整体偏高或偏低时，R2往往不能正确的评价预测效果，而NSE使用平方值计算预测值与观测值之间的差异，对峰值十分敏感却容易忽略低值的预测误差［22］，对比图4（b）和4（d），可看出STL-VMD-SVR 模型的峰值误差更小，使得该模型NSE优于STL-SVR模型。

图4 各组模型测试期预测值和观测值散点图Fig.4 Scatter plots of predicted and observed values in each group of models during the testing period

高流量事件的准确预测对指导流域防洪具有重要意义。从表4中可看出对于测试期三次高流量事件（2015.06、2016.06、2016.07）的预测，Ⅰ组的相对误差介于30%～49%，Ⅱ组介于15%～43%，Ⅲ组介于6%～33%，Ⅳ组介于1%～38%，可见未分解预处理时，各模型对高流量的预测结果普遍较差，而对径流分解预处理有助于提高模型对高流量事件的预测精度，但预测值偏小这一问题依然存在；STL-VMD-LSTM 模型的预测结果整体最优，3 次高流量事件的相对误差分别为12.98%、1.34%和6.61%（2015.06、2016.06和2016.07）。

表4 3次高流量事件预测值及相对误差Tab.4 Predicted values and relative errors of three high-flow events

2.4.3 STL-VMD-LSTM 模型的可解释性分析

综合各评价指标计算结果及高流量事件的预测精度，STLVMD-LSTM 模型为最优模型。为增强该模型的可解释性，采用SHAP 可视化模型解释工具探究各输入特征对预测结果的贡献程度，由1.3 节可知该模型径流序列被分解为趋势项（TRE）、季节项（SEA）和8 个模态分量（V1～V8）并逐一预测，不同目标分量对应输入特征的SHAP 值计算结果如图5 所示（V3～V8 分量振幅较低且计算结果与V2 相似，未对其进行展示）。纵坐标为各输入特征，由上到下其贡献度依次递减，横坐标为SHAP 值，正（负）值表示对模型预测的贡献为正（负），绝对值越大，贡献度越大，点的颜色代表输入特征的值，红色代表最大值，蓝色代表最小值。

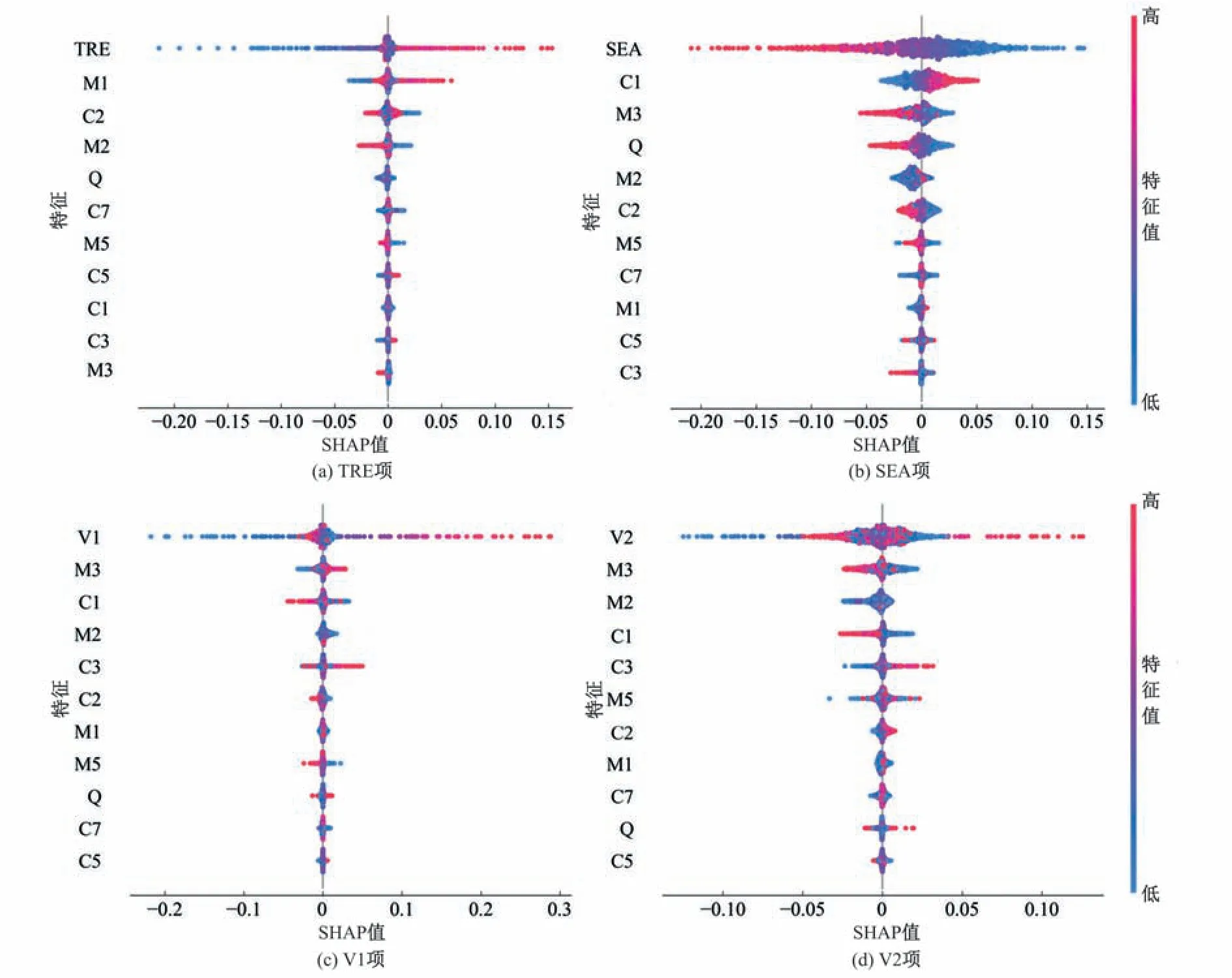
图5 STL-VMD-LSTM 模型输入特征SHAP值Fig.5 Input features SHAP value of STL-VMD-LSTM model

从图5可看出分解后的各分量对预测结果的贡献均优于其他输入特征，进一步验证了两阶段分解对模型精度提升的促进作用；除去目标特征历史序列值外，前期降雨（M1）、NINO1+2（C1）和蒸发（M2）对径流趋势项预测结果贡献较大，其中降雨与SHAP值正相关，表明高（低）降雨值会增大（减小）预测结果，蒸发对预测结果整体贡献为负［图5（a）］，符合客观物理规律，表明该解释结果具有一定的可信度；前期C1和气温（M3）、径流（Q）对径流季节项预测结果有较大贡献［图5（b）］，前期气温、NINO1+2、蒸发对径流残差项的低频分量贡献较大［图5（c）～（d）］；同一因子对径流不同组成的贡献作用可能不同，如对于径流分量V1 的预测，前期气温与SHAP 值正相关［图5（c）］，而对季节项、径流分量V2 的预测，前期气温与SHAP 值呈负相关［图5（b）、5（d）］。

3 结 论

为提高月径流预测精度，根据月径流序列强季节性和高度非稳态的特征，构建了基于两阶段分解（STL-VMD）和机器学习的集成模型，研究结论如下。

（1）两阶段分解预处理可有效地呈现月径流序列的趋势、季节等本质特征，对提升径流预测精度起促进作用，其中对高流量事件预测精度的提升尤为明显，STL-VMD-LSTM 模型为最优模型，测试期MAE、MAPE和NSE分别为55.65 m3∕s、9.61%和0.93，较单一的LSTM 模型分别改善了56.33%、66.44% 和49.18%；

（2）基于SHAP 值对STL-VMD-LSTM 模型进行了可解释性分析，分析结果表明历史降雨、NINO1+2、蒸发对径流趋势项预测贡献较大，历史NINO1+2、气温、Q 对径流季节项预测贡献较大，历史气温、NINO1+2、蒸发对径流残差项低频分量预测贡献较大。