转体斜拉桥索力的确定研究

赵康、方正

（贵州省交通规划勘察设计研究院股份有限公司，贵州贵阳 550000）

1 转体斜拉桥索力确定方法

1.1 概述

从结构理论来讲，斜拉桥合理成桥索力的确定只需对成桥状态下的桥梁进行分析计算而不用考虑施工过程。实际成桥索力则与斜拉桥的施工方法及步骤有关，为达到实际成桥索力与合理成桥索力的一致，通常需进行索力调整。斜拉索张拉次数会影响工程施工效率，如何既能减少张拉次数又能确保桥梁满足受力要求是斜拉桥建设过程中面临的问题之一。目前，施工中主要采用“一次张拉法”和“两次张拉法”进行索力张拉。

目前，斜拉桥合理索力的理论确定方法主要有：最小弯曲应变能法、无应力状态控制法、影响矩阵法、应力平衡法等。以下主要介绍影响矩阵法[1]。

1.2 影响矩阵法

应用影响矩阵法确定斜拉桥索力需要定义受调向量、被调向量及影响向量。

受调向量：斜拉桥n个拉索调整值组成的列向量，定义为：

被调向量：为了改变整体结构内力、变形等指标，可以被调整的n个未知索力组成的列向量，定义为：

式（2）中：xi=()i=1,2,3,...,n为被调截面的位移或者内力。

影响向量：斜拉桥体系索力组中某个索力发生单位变化，造成其他索力的变化值组成的向量，定义为：

影响矩阵：斜拉桥体系索力组中n个索力发生单位变化，引起其他n个索力变化的影响向量组成的矩阵，定义为：

假设桥梁结构适用线性叠加原理，则有：

式（5）中：[A]为影响矩阵；{X} 为被调向量；[B]为受调向量。

影响矩阵的计算是应用影响矩阵法的关键，矩阵中的元素对应斜拉索的应力、变形量等[2]。

目前求影响矩阵的方法主要有：修改总刚度矩阵法、基于强迫变形的影响矩阵法和基于结构连续变更生成影响矩阵法。

对于斜拉桥索力确定，需要分别去掉每根斜拉索，然后沿拉索方向用单位力代替，由于每次去掉一根斜拉索，结构的刚度也随之变化，因此需要多次计算[3]。

2 斜拉桥转体前索力确定

2.1 张拉次数确定

斜拉桥的索力对结构的受力状态有着直接影响。因此，确定施工阶段中索力的张拉大小以及张拉次数是施工的关键。斜拉索张拉次数应尽可能少，但要保证在张拉过程中主梁与主塔的应力在控制范围内，避免出现超应力现象[4]。

实际施工中，一般采用“一次张拉法”或“两次张拉法”进行拉索的张拉。以某市政转体斜拉桥为例。

首先采取“一次张拉法”进行有限元仿真分析。根据计算结果，采用“一次张拉法”，斜拉桥结构在成桥状态的受力是合理的，但在施工阶段，斜拉索逐根张拉会导致主梁被拉起脱离支架，主梁局部出现超应力现象。因此，在施工过程中必须采取有效措施防止出现超应力现象。

目前，消除施工阶段出现超应力现象的方法主要有三种。

一是在斜拉索张拉之前，在主梁上进行临时配重，待张拉完之后再逐步进行卸载。但该措施在实际施工中不易操作，且配重耗资耗力耗时，卸载过程也不易控制。

二是通过专门配置预应力筋来抵消张拉过程中产生的不利应力。但是，在斜拉索张拉完之后，多余配置的预应力筋将不起任何作用，甚至起到反作用。

三是采用“两次张拉法”，即第一次张拉到设计索力的75%左右，待斜拉桥二期恒载等铺装完毕后，再进行第二次张拉至设计索力。该办法操作简单，不需要配置多余的预应力和配重措施，只需要对斜拉索进行两次张拉操作。

因此，经过综合考虑，最终决定采取“两次张拉法”对斜拉索进行张拉的施工方案。

2.2 初张索力的取值优化

该转体斜拉桥采用“两次张拉法”进行调索。第一次张拉是在桥梁转体前且主梁在满堂支架上浇筑完毕并张拉预应力后进行。此时，辅助墩已施工完毕，其上方预留空间为60cm，其中，支座需40cm，垫层约10cm，楔形块最高处约10cm，因此，转体过程中主梁梁端标高需进行严格控制，否则，将导致转体梁不能顺利通过辅助墩。为防止主梁在转体过程中被辅助墩限制，本文在确保主梁不出现超应力现象的前提下，对比分析了初张索力为设计索力的60%、70% 和80%时的主梁线形（见表1），并确定最优的初张索力。

表1 不同初张索力对主梁梁端挠度影响

由表1 数据可知：初张索力值分别为设计值的60%、70% 和80% 时，辅助墩侧梁端竖向挠度值分别为-48.9cm、-41.2cm、-33.4cm，即在确保主梁不出现超应力现象的前提下，初张索力值越大，主梁挠度越小。根据上述计算结果，为确保主梁转体成功，理论上可采取如下两种方案。

方案1：对主梁中跨侧梁端进行配重，在辅助墩墩顶处预留足够的空间让转体梁通过，不同的初张索力值，转体前主梁的配重方案也不同。

方案2：桥梁在转体前不安装辅助墩支座，待转体成功后，再在辅助墩处搭设支架，利用顶推法安装辅助墩支座。

方案2 由于采用顶推法安装辅助墩支座，施工空间有限而难以保证施工质量，因此不建议采纳。而方案1 采用主梁配重的方法，由上述计算结果可知，初张索力越大，配重越小，因此，该桥建议采用初张索力取设计索力的80%（见图1、图2）。

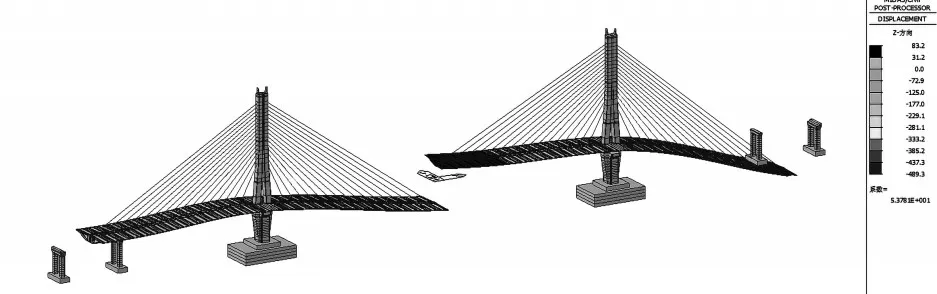
图1 60%设计索力转体前主梁挠度

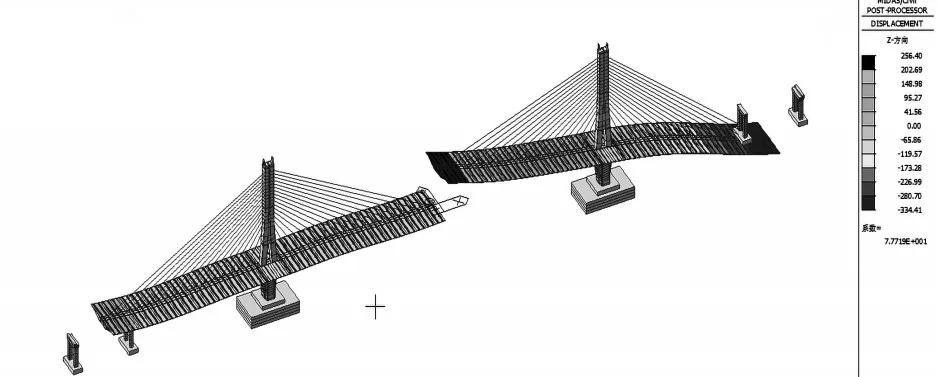
图2 80%设计索力转体前主梁挠度

2.3 初张索力后与实测索力对比

该桥初张索力为设计索力的80%。将该初张索力代入有限元模型中进行正装计算，计算结果表明：在16 对斜拉索张拉过程中，主梁、主塔均未出现超应力现象。索力张拉完之后，采用频率法对索力进行实测，索力编号如图3 所示，结果如图4 和表2 所示。

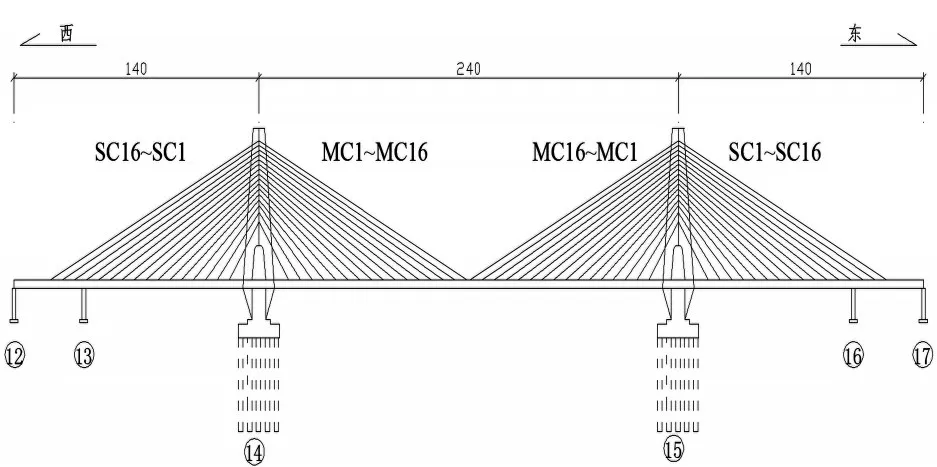
图3 斜拉索编号示意图（t）

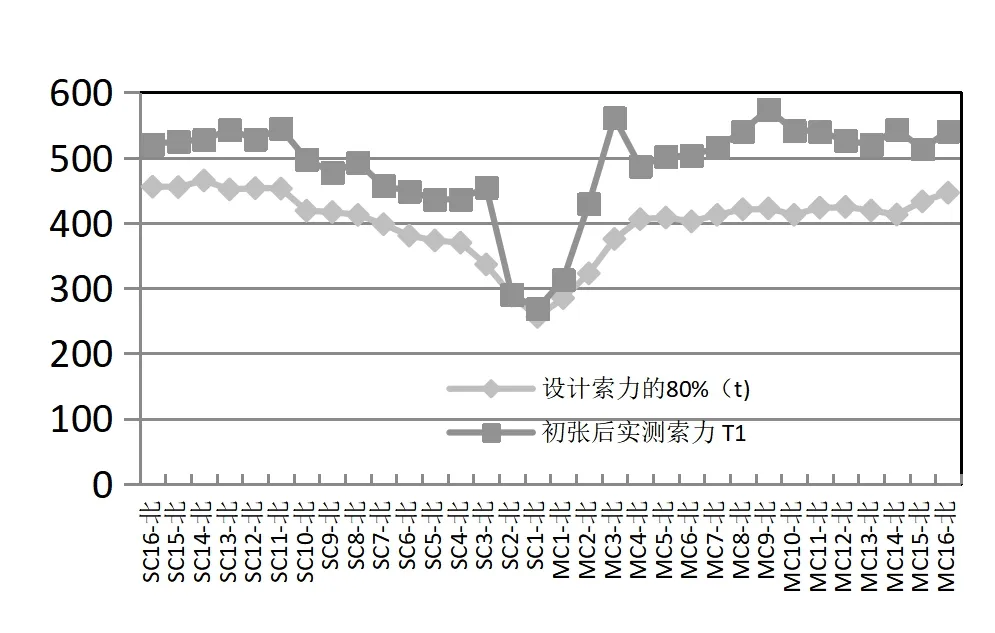
图4 主塔南侧初张后索力与初张索力对比图（t）

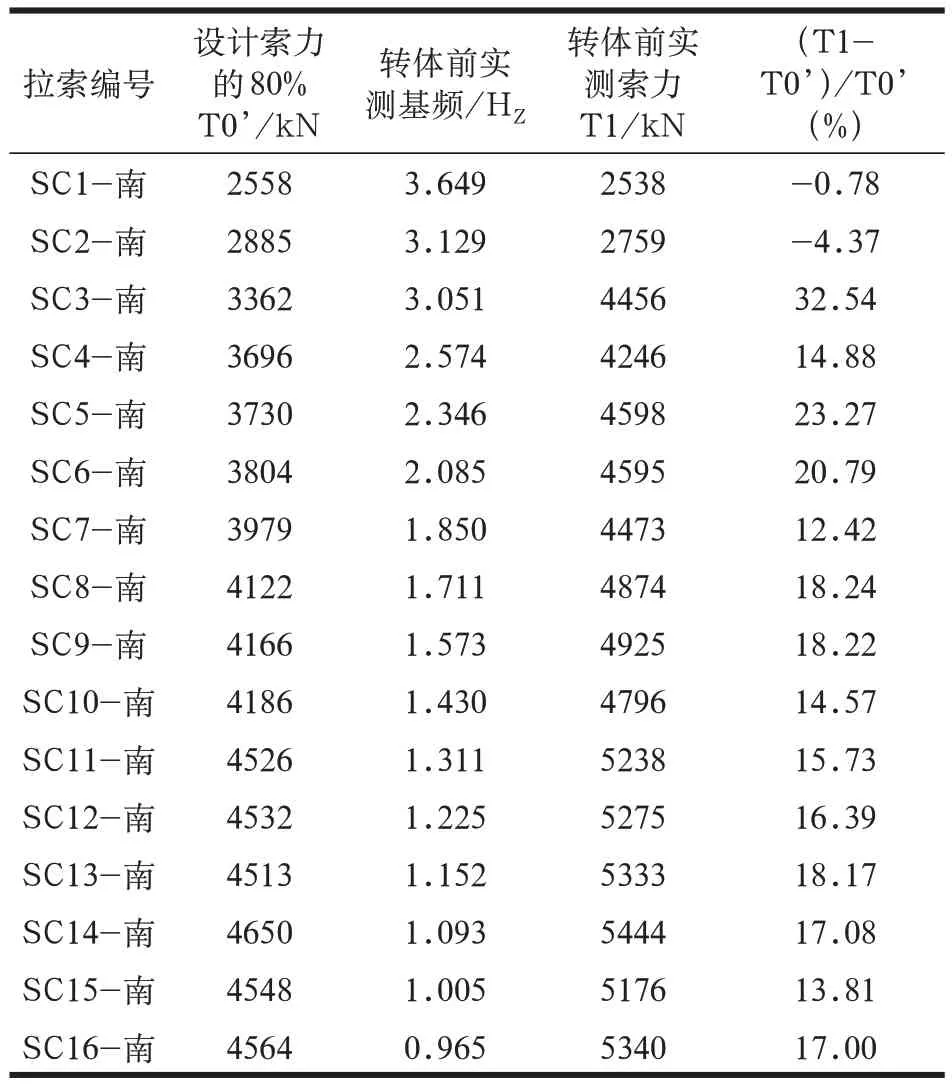
表2 主塔初张后实测与初张索力对比

3 斜拉桥转体成桥后终张索力调整

转体前，主梁与主墩处于临时固结状态，转体完成后，解除临时固结，对桥梁进行合龙、桥面铺装等作业。桥梁体系经历多次转换，因此，桥梁的受力状态和索力均发生变化。桥梁进行第二次张拉的目的是使实际索力值达到设计索力的100%，为此，利用影响矩阵法对索力进行调整。

该桥共64 对斜拉索，因此，索力的影响矩阵为64×64 阶，成桥后斜拉索第二次张拉完毕的实测索力与设计索力对比如表3 所示。成桥后斜拉索第二次张拉完毕的实测索力与设计索力对比如图5 所示。可见，二次张拉结束后，桥梁的实测索力与设计索力接近，误差在±5% 内，满足规范要求，桥梁受力状态良好。

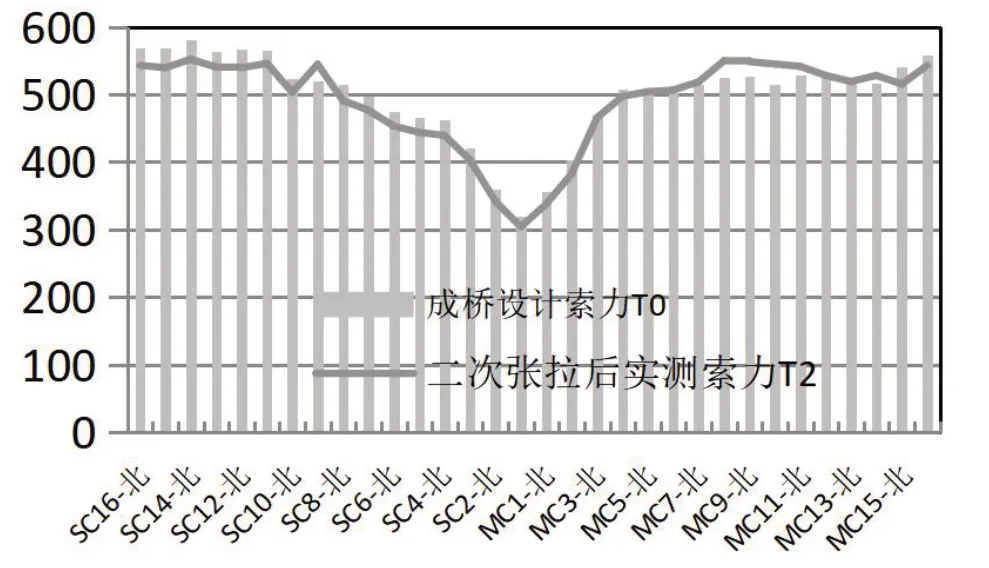
图5 主塔南侧二次张拉完毕索力对比（t）

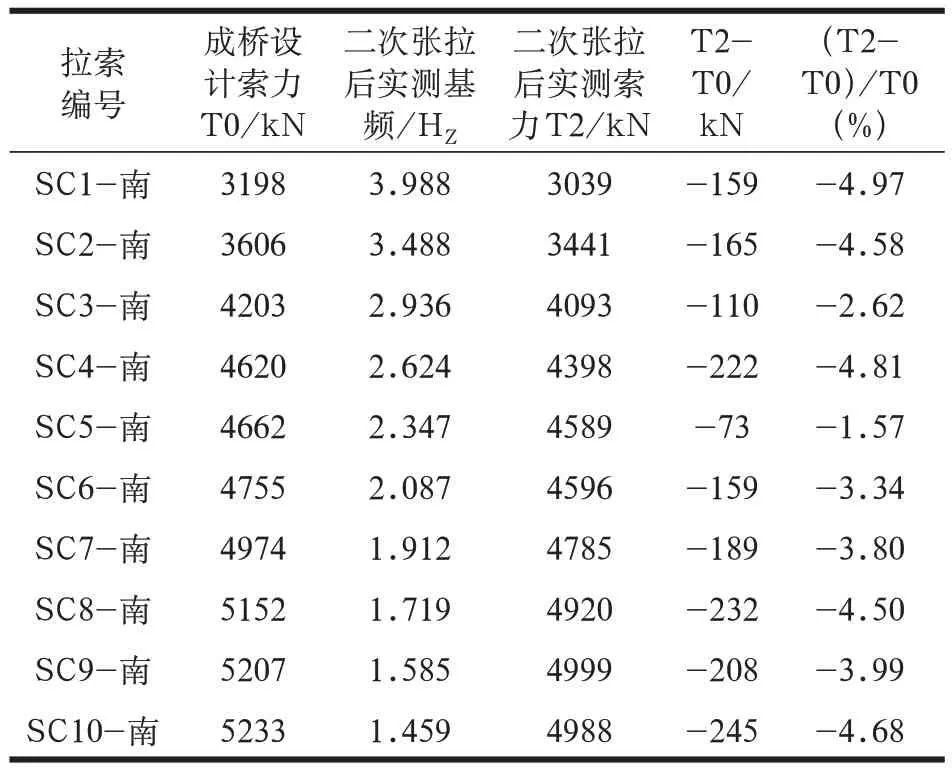
表3 主塔二次张拉完毕实测索力与设计索力对比

4 结论

通过上述对于斜拉桥转体前后索力的理论方法介绍和与实际施工实测索力的对比，得到以下结论。

第一，确定斜拉桥合理索力采用影响矩阵法可满足实际施工需要，切实可行。

第二，斜拉索索力对转体斜拉桥受力状态及配重方案影响较大。对于转体斜拉桥，若采用“一次张拉法”将导致施工过程中主梁出现超应力现象，不建议采用。若采用“两次张拉法”，初张索力合理取值宜为设计索力的80%，能确保主梁不出现超应力现象且使转体不受辅助墩限制，配重也较轻；转体成桥后，采用影响矩阵法进行索力第二次张拉，结果表明，该方法准确有效，实测索力与设计索力误差在±5%内。