结合近邻传播聚类的世界生成神经网络优化器
陆敏芳, 宗 伟, 陈美涵, 杨 波, 王 琳, 张 波
(济南大学 信息科学与工程学院, 山东 济南 250022)
在真实世界的问题中,随着问题特征日益复杂,大多数工程问题逐步演变为一种黑盒问题,即问题内部的具体解析式或工作方式未知,只能够利用问题的输入值和输出值进行求解,因此,黑盒优化算法的发展对于优化属于黑盒范畴的真实问题变得尤为重要。
黑盒问题的自身性质决定了设计高质量解的黑盒优化算法十分困难。早期多用数学推理的零阶方法[1]来解决黑盒问题,如单纯形法和拟牛顿法;但是,这些算法极度依赖问题数学性质,因此难以解决日益复杂的黑盒问题。适用范围更加广泛的群智能启发式算法,如遗传算法(GA)[2]、粒子群优化算法(PSO)[3]等逐渐成为研究热点,然而这些算法需要对复杂的真实问题进行多次评估,代价昂贵。分布估计算法[4]采用基于搜索空间的进化算法,具有较强的全局搜索能力;然而,该算法容易对解空间分布产生过拟合现象,限制解的多样性以及算法的搜索能力,因此,设计一种所需评估次数更少同时种群多样性更高的算法对有效解决黑盒问题具有重要意义。
本文中提出一种新的黑盒优化算法, 即结合近邻传播聚类的世界生成神经网络优化器(AP-WGNN)。 AP-WGNN由2个神经网络(世界模型、 采样生成器)和近邻传播聚类(affinity propagation clustering, AP)[5]的选择策略组成, 通过对问题景观结构进行建模并增加种群多样性, 使得该算法能够以更少的评估次数发现最优解所在的最优分布。 AP-WGNN首先通过2个神经网络的协同优化驱动生成候选解, 增强了对问题景观的学习, 即使用世界模型转换样本, 并基于当前的世界模型通过采样生成器生成解决方案, 减少对真实问题的评估。 然后通过将聚类间排序和聚类内排序相结合的AP的选择算法提高了种群多样性, 提高AP-WGNN找到最优解所在最优分布的概率。 为了验证AP-WGNN的优化性能, 本文中分别在多个维度上对比AP-WGNN和其他5种基线算法的优化结果, 从不同角度验证AP-WGNN的精度和稳定性。
1 协同学习神经网络
AP-WGNN由世界模型、 采样生成器和基于AP的选择策略组成。 历史解集由均匀分布随机初始化。 在每次迭代中, 世界模型通过历史解集及其适应度的不断训练来逼近真实问题景观。 本文中适应度表示解的质量优劣。 适应度越低, 质量越好。 与此同时, 根据当前的世界模型, 对采样生成器进行训练, 以产生更好的解。 通过AP、 簇间排序、 簇内排序的共同合作, 得到更好的解, 组成新的历史解集。 AP-WGNN的框架和流程如图1、 2所示。

图1 结合近邻传播聚类的世界生成神经网络优化器框架
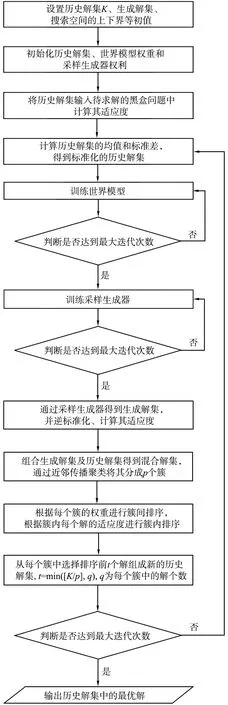
图2 结合近邻传播聚类的世界生成神经网络优化器流程图
1.1 世界模型
由于黑盒问题的评估代价是昂贵的,因此在不了解问题景观的情况下进行优化会显著增加评估成本。为了解决这个问题,世界模型被设计为一个动态代理模型[6],通过持续训练使其近似真实的黑盒问题景观。同时,世界模型通过减少真实适应度和代理适应度之间的误差,使生成的解更接近真实解。为了使训练过程稳定,加快训练速度,AP-WGNN采用Z分值(Z-score)归一化方法[7]将解的不同维度都缩放至标准化区域。Z-score公式为
xscale=(xhis-μ)/σ,
(1)
xunscale=xgσ+μ,
(2)
式中:xscale为历史解集的标准化形式;xhis为历史解集;μ和σ分别为xhis的均值和标准差;xunscale为采样生成器G的输出xg的逆标准化。在对xhis进行Z-score归一化后,xscale被用作世界模型的输入。经过多次训练迭代后,可以获得近似真实的黑盒问题景观的代理模型。世界模型W损失函数表达式为
(3)
式中:K为历史解集的规模;fhis,i为历史最优解集fhis中的第i个元素,表示xhis,i的适应度;W(xscale,i)表示归一化后的最优解集xscale,i通过世界模型W拟合的适应度。 当世界模型进行训练时, 神经网络的损失函数逐渐趋于0, 意味着世界模型逐渐学会了该黑盒问题, 输出的拟合适应度逐渐接近真实的适应度。
1.2 采样生成器
世界模型可以学习由xhis表示的问题的局部结构,以近似地描述问题的情况。采样生成器G通过世界模型生成新的适应度更好的解xg。采样生成器G的损失函数表达式为
(4)
式中:m为生成解集的规模;η为正态分布,代表输入到采样生成器G的随机噪声,产生xg。随着采样生成器G的训练,损失函数的值逐渐趋于0,意味着采样生成器的适应度逐渐趋于0,因此,采样生成器将生成具有更好适应度的解。
AP-WGNN通过世界模型增强了对问题的先验知识的获取,并通过采样生成器提高了算法的挖掘能力,使其能够在世界模型学习到的问题景观中找到更好的解。
2 基于AP的选择策略
2.1 AP
AP可以在不指定聚类数量的情况下自动将解集分为多个簇,增加了搜索的多样性,避免增加额外的超参数,因此,AP-WGNN可以避免过早地陷入局部最优,并且所选方案具有低相似度,可以使AP-WGNN以更高的概率找到全局最优。AP通过欧氏距离计算相似度矩阵,从而更新责任矩阵和可用性矩阵。经过AP,历史解和生成解的混合解集xmix被分为p个簇,每个簇中的解的数量为q,p和q在优化过程中由AP产生并自适应变化,表达式为
(5)
式中:xcdata,i是第i个簇中的解;xcenter,i是xcenter的第i个元素,代表簇的中心样本。
2.2 簇间排序选择策略
AP将xmix划分成具有高度多样性的多个簇。这些簇根据簇中所有解的平均适应度进行排序,作为这个簇的权重。权重较小的簇表示该簇中的解质量较高。每个簇的权重公式为
(6)
式中:Vcenter,i为第i个簇的平均适应度;fcdata, j为第i个簇中第j个解的适应度。通过簇间的排序选择,选出平均适应度较高的簇,帮助AP-WGNN筛选出质量更优且多样化的解。
2.3 簇内排序选择策略
簇间排序选择后,对同一簇中的解分别按其适应度进行排序。AP-WGNN通过从每个簇中选择前t个解,形成一个新的历史解决方案集xhis。选择方法表达式为
(7)
式中t=[(K/p)],i=1,2,…,p。如果被选择的解的总数少于K,AP-WGNN将从剩余未被选择过的解中选择,直到新的历史解集中解的数量等于K。
3 数值实验
对AP-WGNN进行数值分析,所有实验使用的测试问题从比较连续优化器平台(platform for comparing continuous optimizers, COCO)平台[8]选择,包括Sphere、 Ellipsoidal、 DifferentPower等12个黑盒基准问题(具体如图3所示)。
3.1 优化过程可视化
图3所示为12个COCO平台上的基准黑盒问题的三维景观和在二维等高线图上AP-WGNN的最优点的寻优轨迹。从图中可以看出,如果问题是单峰的,如Sphere和Different Powers,AP-WGNN会逐渐找到全局最优;当问题为多峰时,如Buche-Rastrigin,AP-WGNN将首先通过挖掘能力找到局部最优区域,然后,通过探索能力跳出局部最优,找到全局最优区域。由此可以看出,AP-WGNN通过神经网络和AP选择策略,不仅提高了挖掘能力,也提高了探索能力。
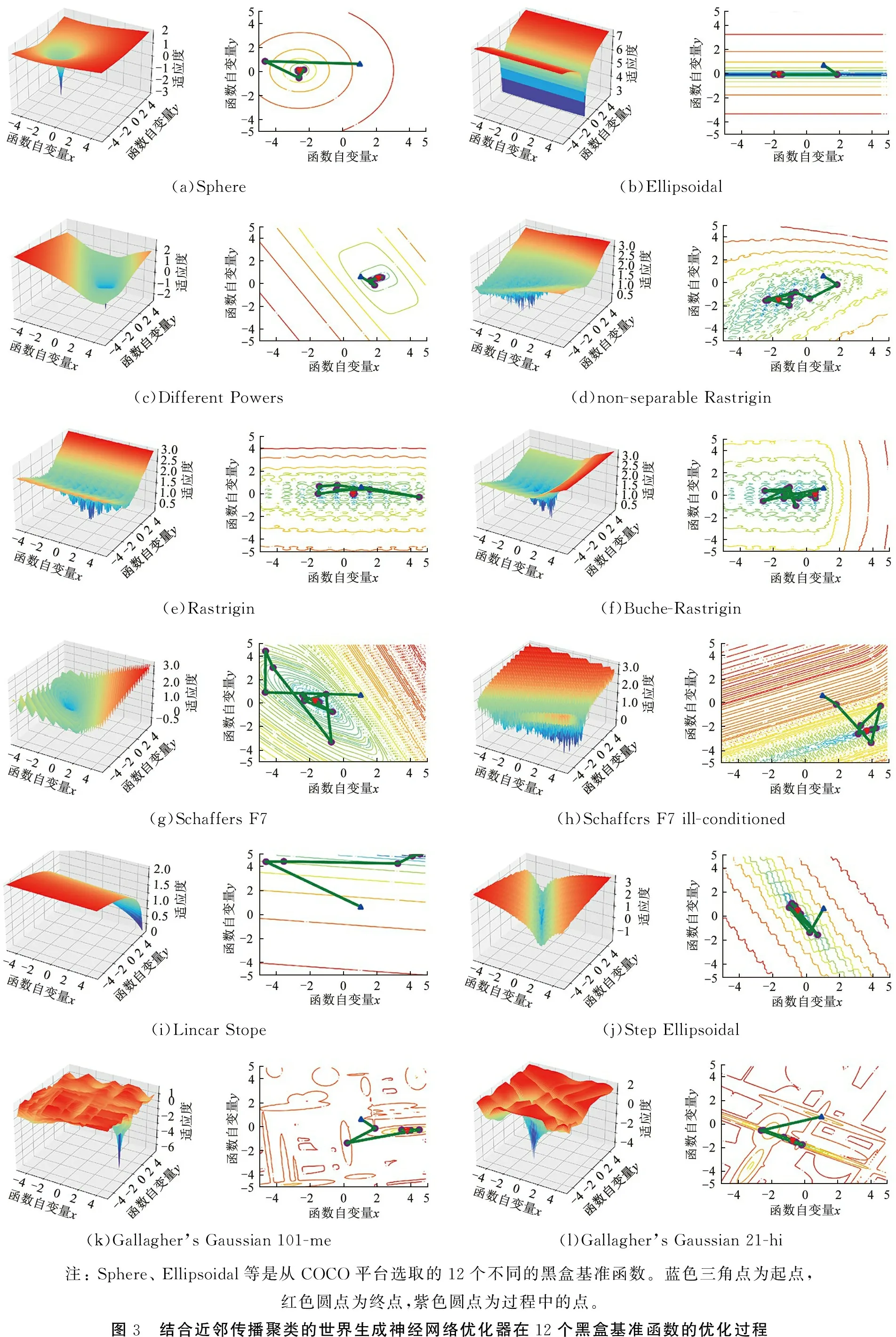
3.2 性能分析
以下采用5种启发式优化器作为对比算法验证AP-WGNN的优化性能。在基于神经网络的优化算法中,将显示梯度估计算法(EGL)[9]作为对比算法。在传统启发式优化算法中,分别选择Nelder-Mead(NM)[10]、 BFGS[11]、 PSO[12]和GA[13]4种具有代表性的算法。在实验中,从COCO平台中选取上述12个包含不同属性的具有挑战性的黑盒基准函数。所有基准函数在2、 3、 5维上运行15次。在所有维度中,函数评估次数的最大值设置为50 000。对于实验中使用的基准函数,适应度越小表明方法的性能越好。
图4所示为AP-WGNN、 GA、 PSO、 EGL、 NM和BFGS算法在不同2维黑盒基准函数的收敛曲线。 可以看出, AP-WGNN在所有基准函数的测试上都具有良好的性能, 在Sphere、 Linear Slope、 Different Powers等单峰问题上,AP-WGNN的优化效果与其他算法的相当,性能基本相近。

当算法具有较强的挖掘能力时,对于单峰问题可以很容易地找到较好的解,然而,当面对多峰病态、全局趋势不明显的问题时,如Rastrigin、 non-separable Rastrigin,算法不仅需要具备挖掘能力,还需要有足够的探索能力,才能从多个局部最优区域中找到最好的解。AP-WGNN在这2个基准函数测试上的性能最好,说明它具有比其他算法更好的探索能力,原因是AP-WGNN对问题的景观有足够的了解,从而强化了挖掘能力,同时使用AP选择策略选择多样性的解可以提高算法的探索能力。
特别是针对Gallagher’s Gaussian 21-hi 和Gallagher’s Gaussian 101-me问题, 要寻找由许多位置和高度不相关的最优解组成的局部最优区域对算法更有具挑战性, 更能判断算法的全局探索能力的强弱。 无论是EGL, 还是传统的启发式算法, 即使给出充分的求解次数, 在这2个问题上都只能找到局部最优。 AP-WGNN得益于神经网络的拟合能力及AP选择策略的探索能力, 其优化性能远优于其他算法, 且需要的评估次数更少。 为了全面分析在有限的函数评估次数下可以达到的最优精度, 表1给出了6种算法在2、 3、 5维黑盒基准函数不同精度下的平均适应度。 从表中可以看出, 随着维数的增加, AP-WGNN的平均适应度的排名有所下降, 但下降幅度明显小于其他算法, AP-WGNN仍然排名第一。 无论在哪个维度上, BFGS和NM的排名始终较低。 同时, 精度要求越高, 所有算法的排名会降低, 但AP-WGNN的排名下降幅度远远小于其他5种算法的, 表明AP-WGNN在不同精度要求时的表现都是最好的。
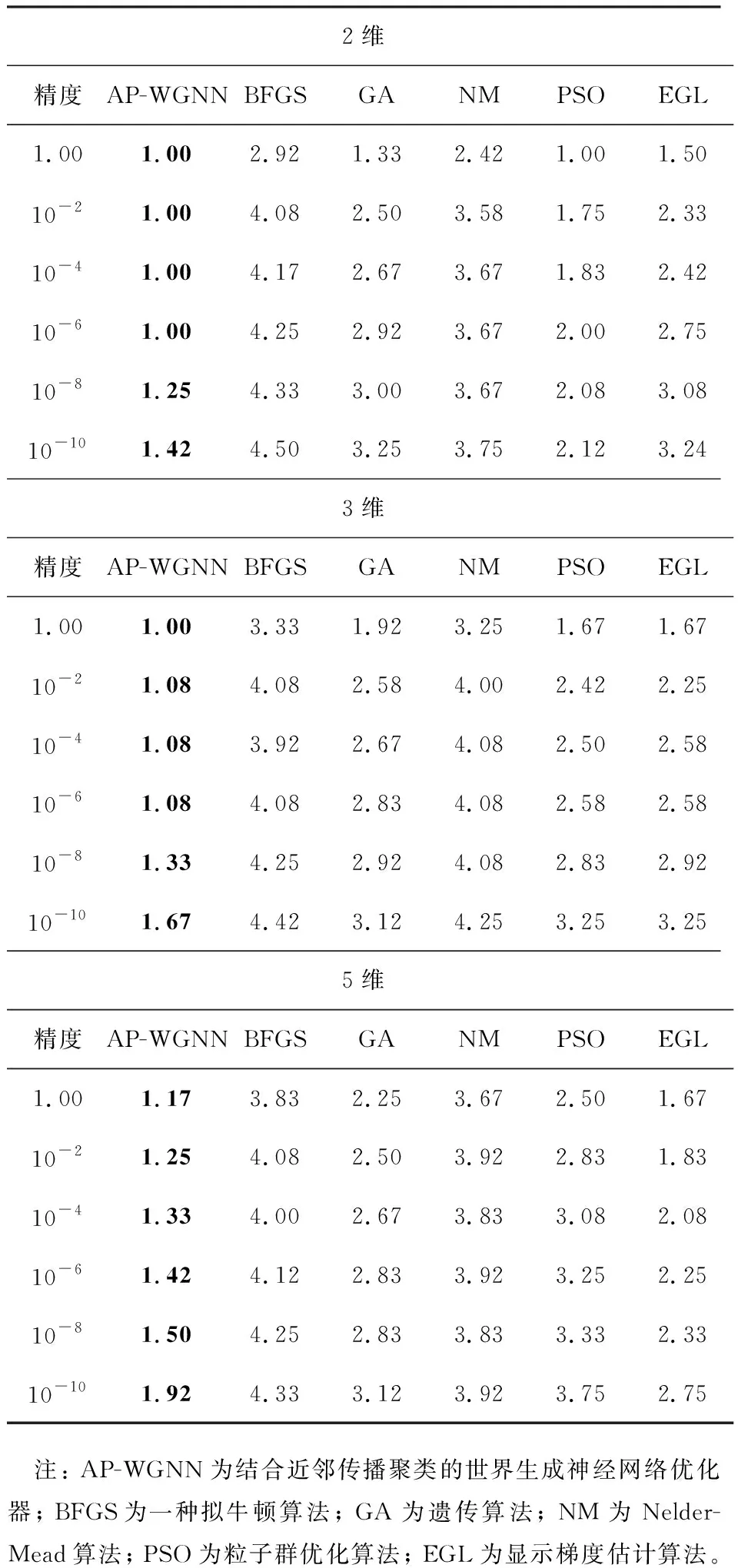
表1 不同算法在不同维度黑盒基准函数的平均适应度
表2给出了不同算法在2、 3、 5维的12个黑盒基准函数上的t检验结果。 显著性水平设置为0.05。 结果表明, AP-WGNN在多个维度上总体性能都要优于其他算法。 当维数为2时, PSO的性能优于AP-WGNN的, 但随着维数的增加, PSO的性能迅速下降, 说明AP-WGNN在维数为3、 5时具有更好的适应性。
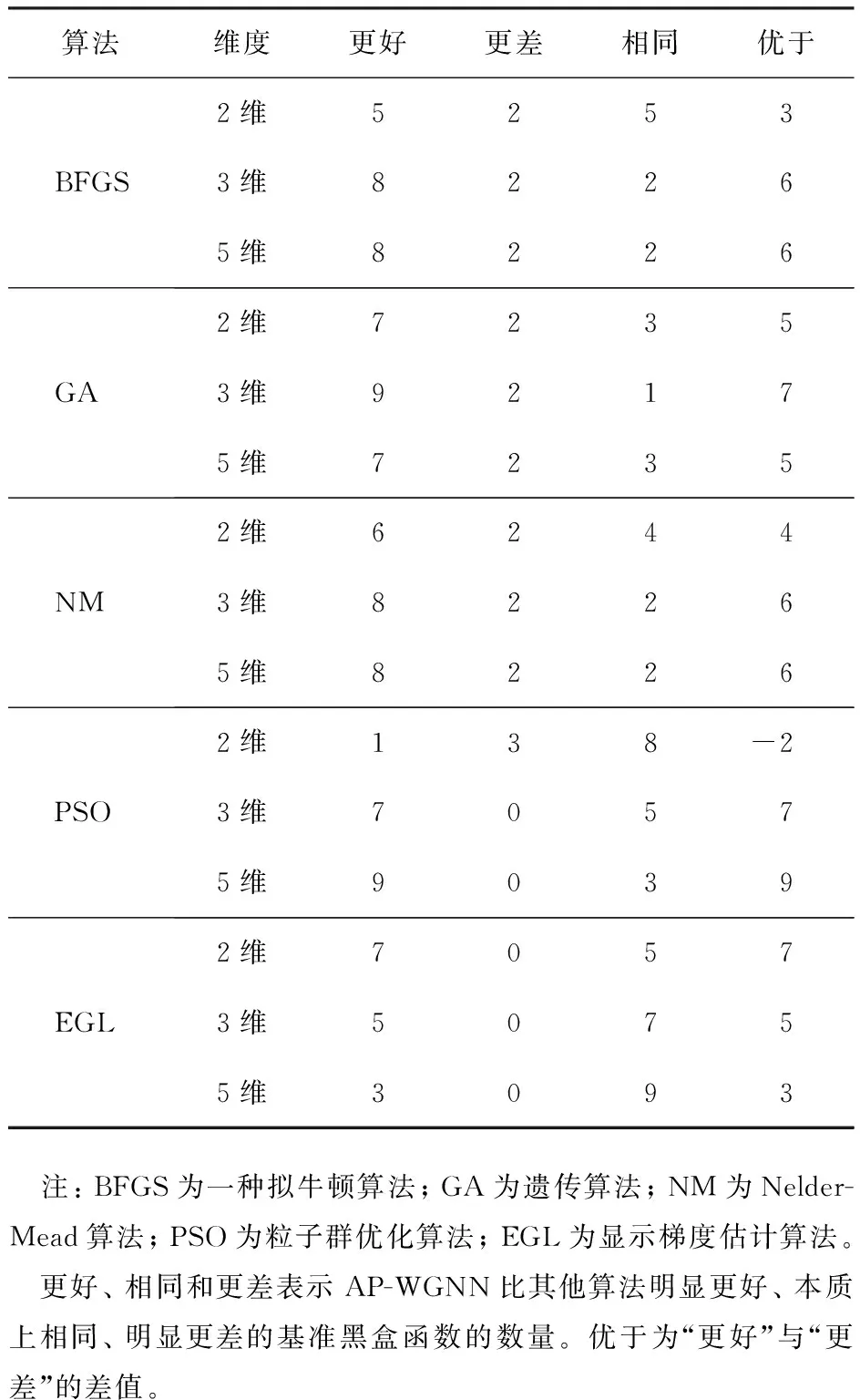
表2 不同算法在不同维度黑盒基准上的t检验结果
3.3 参数分析
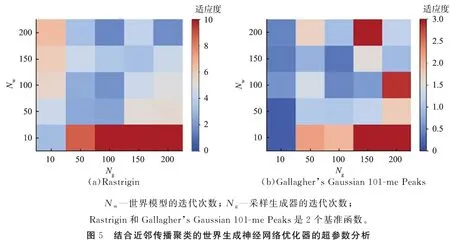
图5所示为AP-WGNN的世界模型的训练迭代次数Nw和采样生成器的训练迭代次数Ng的超参数分析。Nw影响世界模型W的训练频率,Ng则影响采样生成器G的训练频率。 AP-WGNN在2个5维基准函数上重复运行15次, 最大函数评估次数为10 000。 从图中可以看出: 当Nw和Ng设置为相似值时, AP-WGNN的性能更好; 当Nw较小时, 无论Ng多大, AP-WGNN的性能都很差, 说明G的训练只有在W被充分建模时才有效, 因为G是根据当前W生成样本的; 当Ng和Nw较小时, AP-WGNN在2个基准函数的性能差异较大, 说明在此设置下AP-WGNN的性能是不稳定的, 因此, 建议将Nw和Ng设置为[50,100]。
4 结语
本文中提出了一种新的协同学习神经网络黑盒优化器AP-WGNN,用以解决复杂的黑盒优化问题。在AP-WGNN中,世界模型和生成神经网络被协同训练以产生真实的、更好的解;然后,AP将历史解集和生成解集的混合集划分为多个簇,同时,根据簇的权重对不同的簇进行排序, 并对同一簇中的解按适
应度大小进行排序,被选择的解将组成新的历史解集;最后,通过综合实验验证了所提方法的有效性。为了进一步提高该方法的效率,今后将采取更好的启动策略,如改进初始化策略,比较不同建模方法对算法的影响。此外,未来还将继续研究该方法在高维问题上的实际应用。

