人工蜂群算法改进水波优化算法的云资源调度性能
宋 颖, 梁卫芳, 赵 珏, 张福泉, 侯小毛
(1.湖南信息学院 计算机科学与工程学院, 湖南 长沙 410151, 中国;2.湖南工商大学 计算机学院, 湖南 长沙 410205, 中国; 3.菲律宾国家大学 计算机与信息技术学院, 马尼拉 0900, 菲律宾;4. 闽江学院 计算机与控制工程学院, 福建 福州 350108, 中国; 5. 湖南化工职业技术学院 自动化与信息工程学院, 湖南 株洲 412000, 中国)
云计算是当前大数据服务端的主要形式之一,云端所有资源经虚拟化后被统一管理、分配给使用云平台的所有任务[1]。对于云计算的用户端来说,用户最关心任务的是执行时间及服务质量,而云计算服务端希望采用最少的资源来提供用户满意的服务,这两者均与云资源的合理调度有关。云资源调度使资源和任务的动态分配得以实现[2]。当资源量相对于任务量较充裕时,用户端的实时访问需求比较容易满足,但是实际情况是,为了节省能耗和降低计算资源成本,云计算服务端所提供的资源量往往有限。目前关于云资源调度的研究主要是集中在资源量受限的情况下采用各种算法来实现资源-任务的动态精细分配。
当前,关于云资源调度的研究较多,其中的一个重要研究方向就是各种群智能算法在云资源调度场景中的应用。例如,孙力等[3]将量子遗传算法和蚁群优化算法组合用于云资源调度,通过群智能算法搜索最佳调度参数组合,即最优个体。郑春梅等[4]采用差分进化算法用于云资源调度,并且为了提高调度效率,对差分缩放因子进行自适应优化。上述研究均采用群智能算法来实现云资源调度,表现出了较好的执行效率,但是,这2种云资源调度算法均侧重于调度时间,仅将调度执行时间作为目标函数进行优化,没有考虑任务成本或者负载均衡等指标,而且调度的任务数量并不多。
本文中尝试将水波优化(water wave optimization,WWO)算法[5]应用于多目标函数的云资源调度,将资源-任务集抽象成多个水波个体,通过水波的运动操作来求解资源-任务分配的最优个体,从而获得调度分配参数组合。为了改善WWO算法的资源调度性能,将人工蜂群(artificial bee colony,ABC)算法用于WWO算法的核心参数优化求解,通过ABC算法的蜜源搜索优化方式,获得最优核心参数,以最优核心参数构建的云资源调度模型,力求资源调度性能更好。与标准WWO算法相比,ABC-WWO算法的承载任务量分布更均匀且负载均衡指标更小。
1 WWO算法
WWO算法主要是通过水波的3种运动方式来实现优化求解。

(1)

波长更新方式[6]为
λ′=λα-(f(x)-fmin+ε)/(fmax-fmin+ε),
(2)
式中:λ′为更新后的波长;α为水波衰减系数;ε为大于0且近似于0的数。
2)折射操作。设水波xd服从高斯随机分布函数N(μ,σ),
(3)
(4)
式中μ、σ分别为均值和标准差。
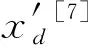
(5)
波长求解公式[8]为
(6)

(7)
式中β为碎波系数。
2 基于ABC-WWO算法的云资源调度模型
2.1 ABC-WWO算法
ABC算法通过蜜蜂的蜜源i搜索完成既定范围内的寻优操作。设蜜蜂总维度为D,侦测蜂在第d维搜索边界[Ld,Ud]的运动位置为Xid[10],
Xid=Ld+rand(0, 1)×(Ud-Ld)。
(8)
假设蜜源i的第d维坐标为Vid,侦测蜂Xid寻找蜜源的移动操作[11]为
Vid=Xid+φ(Xid-Xjd),
(9)
式中j≠i,表示不同于蜜源i的另一个蜜源;φ为[1,1]的随机值;Xjd为搜索边界[Ld,Ud]内排除Xid以外的任意坐标。
侦测蜂每运行一次将其记录的旧蜜源和新蜜源Vi=[Vi1,Vi2,,Vid]进行适应度值对比,以更新蜜源,适应度求解函数Fi[12]为
(10)
式中fi为第i个蜜源的适应度,对比Vi和Xi,选择两者适应度高的作为新蜜源。
侦测蜂将蜜源信息广播给追随蜂,追随蜂有自由选择蜜源的权利,按照概率pi选择蜜源[13],即
(11)
式中S为侦测蜂获得的所有蜜源数。
当迭代次数G满足时G=Gmax,输出当前蜜源坐标即为最优解,算法停止,否则转到式(8)—(11)继续迭代。
2.2 云资源调度模型的构建
云资源调度模型的主要任务是将n个任务分配至m个云资源中,因此,首先需要根据任务的执行的资源需要,可以构建任务-资源矩阵,其中第t个任务对第r个资源的执行时间为M(t,r),则任务t在资源r上的执行完毕时间Mct(t,r)为
Mct(t,r)=Ms(r)+M(t,r),
(12)
式中Ms(r)为资源r开始被使用的时间。若任务t只需要使用资源r,那么任务t的整个执行时间Ct为
Ct=Mct(t,r)。
(13)
当云计算服务平台的任务并行执行时,云资源调度模型中所有任务的调度时间M为
(14)
在式(12)中, 任务t的执行时间只使用了1个资源(资源r), 当任务需要使用多个资源时, 云资源调度模型将变得复杂。在云资源调度模型的优化研究中, 常将所有任务调度时间作为优化的目标函数。仅将单一的调度时间作为目标函数不符合云计算的现状。 为了解决这个问题, 本文中云资源调度模型将云计算任务调度时间、调度成本及负载均衡度作为云资源调度优化的目标, 提高云资源调度性能。
设该模型的任务t使用的r个虚拟机资源Vr的成本为Rcu(t,r),那么所有任务的成本Q为
(15)
模型的负载均衡指标Id为
Id=(Cmax-Cmin)/Cave,
(16)
式中Cmax、Cmin和Cave分别为所有云资源调度任务中执行时间的最大值、最小值和平均值。
综上,所提云资源调度模型的优化目标变为
F=λ1M+λ2Q+λ3DI,
s.t.λ1+λ2+λ3=1 ,
(17)
式中λ1、λ2和λ3分别为3个优化指标的权重系数。
2.3 模型的执行流程
基于ABC-WWO算法的云资源调度流程如图1所示。初始化云资源调度模型的实例参数组合,将任务、资源、任务的资源使用时间及资源的成本量化并抽象化为不同的水波。WWO算法的适应度函数为云资源调度的所有任务完成时间、虚拟机使用成本和负载均衡指标加权之和的最小值。计算所有水波适应度,并执行水波优化操作。不断更新水波群的最大适应度,且将水波衰减系数α和碎波系数β作为ABC算法的优化对象,从而得到最优个体,即所需云资源调度参数组合。

图1 基于人工蜂群-水波优化算法的云资源调度流程
3 实例仿真
为了验证ABC-WWO算法在云资源调度中的性能, 进行实例仿真, 仿真平台为Cloud Sim, 其中仿真平台提供的任务数量为30~1 000, 参与计算的虚拟机数量为10~100, 所有参与运算的虚拟机配置及优先级均相同, 仿真资源具体配置如表1所示。

表1 仿真平台配置
3.1 WWO的改进性能
为了验证ABC算法对WWO的改进性能,分别采用WWO、 ABC-WWO算法进行云资源调度性能仿真,虚拟机资源数量为m=10,任务执行时间如图2所示。从图中可以看出,在虚拟机资源数量一定时,任务数量的增多将导致云资源调度的时间增加,对比WWO、 ABC-WWO算法发现,在任务数量小于100时,两者的资源调度时间非常接近。当任务数量为100~600时,两者的调度时间虽然都在增加,但WWO算法执行时间增加更快,2种算法的执行时间差距逐渐增大,表明经过ABC优化后,WWO算法的云资源调度执行时间明显缩短。

图2 水波优化(WWO)算法和人工蜂群(ABC)-WWO算法的云资源调度时间对比
对2种算法的负载均衡性能进行仿真,差异化设置任务数量,其中10台虚拟机资源分别所承载的任务数量统计结果如表2所示。
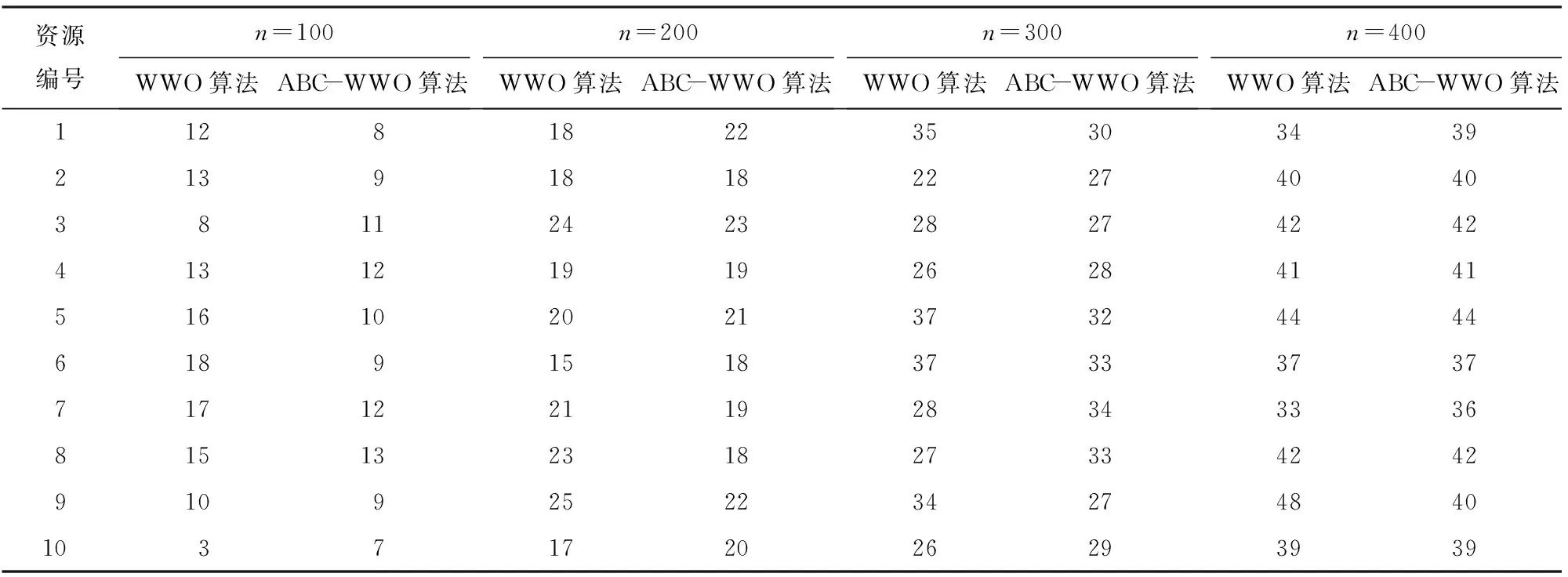
表2 水波优化(WWO)算法和人工蜂群(ABC)-WWO算法的承载任务量
从表2中可以看出,在相同任务的虚拟机资源调度时,与WWO算法相比,ABC-WWO算法的任务量分配明显更均匀,当任务量为100时,WWO算法给虚拟机6分配了18个任务,而给虚拟机10仅分配了3个任务,这种任务分配数量差距过大的情况将导致不同虚拟机“忙”和“闲”分布不均,导致云资源调度性能不佳。当任务量大于100时,WWO算法的调度分配趋于平衡,但与ABC-WWO算法相比,其分配均衡性明显较差。
继续对2种算法的负载均衡指标进行性能仿真,进一步验证2种算法的调度均衡性能,结果如图3所示。由图可见,随着任务量的变化,WWO算法的负载均衡指标值明显大于ABC-WWO算法的,表明WWO算法的执行时间最大值和最小值差值较大,其云资源调度的均衡能力较ABC-WWO算法差。从图中还可以看出,负载均衡指标与任务量的关系不明晰,两者没有呈现规律性变化。

图3 水波优化(WWO)算法和人工蜂群(ABC)-WWO算法的负载均衡指标
3.2 不同算法的云资源调度性能
为了验证不同调度算法的云资源调度性能,分别与采用蚁群优化(ACO)算法[14]、 粒子群优化(PSO)算法[15]、 萤火虫算法(FA)[16]与ABC-WWO算法的云资源调度模型进行仿真对比。
3.2.1 不同任务数量的调度性能
设置资源个数为50,差异化设置使用云资源的任务数量,验证不同算法的资源调度时间,结果如图4所示。由图可以看出:当任务数量小于200时,4种算法的执行时间非常接近,主要原因是虚拟机资源数量为50,与任务数量相比,虚拟机资源比较充裕,调度算法的性能差异不是特别明显;当任务数量为200~1 000时,4种算法的执行时间差异度明显增大,ACO算法耗时最长,FA算法略优于PSO算法,ABC-WWO算法最省时,表明ABC-WWO算法的云资源调度性能最优。

ACO—蚁群优化算法; PSO—粒子群优化算法;FA—萤火虫算法; ABC-WWO—人工蜂群-水波优化算法。图4 资源数量相同时不同云资源调度算法的执行时间
3.2.2 不同资源数量的调度性能
为了验证4种算法在不同资源数量时的云资源调度性能,差异化设置参与云计算的虚拟主机数量,任务数量设置为1 000,验证不同算法的资源调度时间,结果见图5。从图中可以看出,随着虚拟主机数量的变化,ABC-WWO算法的执行时间最短,FA算法的次之,ACO算法的最长。当资源数量小于60时,4种算法的执行时间差异较明显;当资源数量为60~100时,4种算法的执行时间差异度明显减小,原因是虚拟机资源数量增加,各种调度算法的优化性能体现不是特别明显。综上所述,在对云资源进行调度时,云服务平台本身的资源数量对执行时间的影响最为关键,但在资源数量有限时,调度算法的寻优能力就变得尤为重要。

ACO—蚁群优化算法; PSO—粒子群优化算法;FA—萤火虫算法; ABC-WWO—人工蜂群-水波优化算法。图5 任务数量相同时不同云资源调度算法的执行时间
3.2.3 收敛性能
对4种不同算法的收敛性能进行仿真, 验证在资源数量为50时不同算法的资源调度稳定性及效率, 结果如图6所示。 由图可以看出, 虽然任务数量的变化对4种算法的云资源调度执行时间影响明显, 但4种算法的迭代次数差异并不大。 当任务数量为100、 200时, 4种算法的执行时间在迭代80次后达到稳定; 当任务数量为500、 800时,4种算法的执行时间均在迭代90次左右达到稳定。 总之, 从资源调度稳定性来看, 4种算法差距较小, 但从资源调度的执行时间来看, ABC-WWO算法仍占优势。

4 结语
采用ABC-WWO算法用于云资源调度, 通过ABC算法对水波衰减系数和碎波系数的优化求解, 有效提高了WWO算法在云资源调度中的适用性, 相比于基于常用算法的云资源调度模型, 在相同任务数量或者相同资源数量的条件下, 采用ABC-WWO算法均能够获得更优的调度性能, 且云服务平台虚拟机资源负载均衡性方面更为出色,特别适用于云资源的大规模调度。

